11 Solutions and Solubility (part 2) (M3Q2)

Introduction

This section continues to explores aqueous chemical reactions. First, we examine the forces competing when a solid dissolves in water (or not). Second, we examine how chemists use chemical symbols to represent the changes that occur during a precipitation reaction, including writing complete and net ionic equations. The section below provides a more detailed description of these topics, worked examples, practice problems and a glossary of important terms.

Learning Objectives for Solutions and Solubility

 

| Key Concepts and Summary | Glossary | End of Section Exercises |

The Formation of Solutions

The amount of a particular ionic compound that will dissolve in a given quantity of water must be determined experimentally. One can dissolve increasing amounts of a compound in a fixed volume of water at a specific temperature until no more will dissolve and a saturated solution is formed. Even a qualitative prediction of the relative solubility of ionic compounds is challenging as there are many factors involved. Dissolving a solute in a solvent is not as simple a process as melting, for example, although the application of Coulom b’s Law is important for understanding both of these physical processes. Melting can be considered breaking apart the ionic lattice to produce freely mobile ions. Breaking bonds always requires an input of energy and is therefore an endothermic process (energy absorbed). The melting of any substance is always an endothermic process. Ionic compounds with stronger bonds (compounds that contain small, highly charged ions) require a greater amount of energy to separate the anions and cations and therefore have relatively high melting points.

Like melting, the dissolving process also involves breaking apart the ionic lattice but is coupled with a bond-making process as water molecules surround the anions and cations, a process known as solvation or hydration when water is the solvent, as Figure 1 shows.

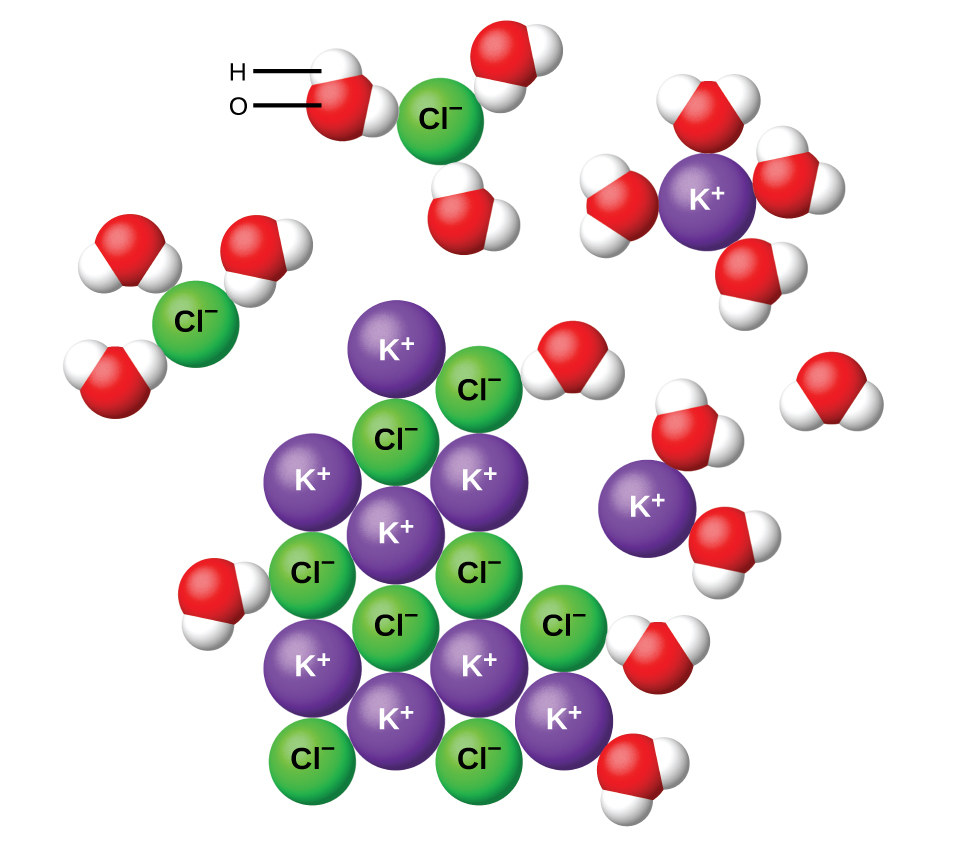
The diagram shows eight purple spheres labeled K superscript plus and eight green spheres labeled C l superscript minus mixed and touching near the center of the diagram. Outside of this cluster of spheres are seventeen clusters of three spheres, which include one red and two white spheres. A red sphere in one of these clusters is labeled O. A white sphere is labeled H. Two of the green C l superscript minus spheres are surrounded by three of the red and white clusters, with the red spheres closer to the green spheres than the white spheres. One of the K superscript plus purple spheres is surrounded by four of the red and white clusters. The white spheres of these clusters are closest to the purple spheres.
Figure 1. As potassium chloride (KCl) dissolves in water, the ions are hydrated. The polar water molecules are attracted by the charges on the K+ and Cl− ions. Water molecules in front of and behind the ions are not shown.
When making bonds results in the formation of a more stable entity—hydrated ions in this instance—energy is released. Whenever energy is released in a chemical or physical change the process is described as an exothermic process (energy released). When a substance dissolves, the number of bonds broken is comparable to those made and so dissolving is usually either a slightly endothermic or exothermic process overall as the bond making (exothermic) and bond breaking (endothermic) steps almost cancel each other out. Compounds that dissolve exothermically are generally quite soluble. However, compounds that dissolve endothermically are not always insoluble, as when a relatively ordered crystalline ionic structure becomes a much more mobile aqueous solution and the matter is spread out. This change from order to disorder is a very powerful driving force for physical (and chemical) processes and is referred to as an increase in entropy. Whenever a substance dissolves, either exothermically or endothermically, there is an increase in entropy.

To summarize, ionic compounds that dissolve exothermically (the energy released through making bonds is greater than the energy input required to break bonds) are usually very soluble. Ionic compounds that dissolve endothermically (the energy released through making bonds upon hydration is less than the energy input required to break bonds) are often insoluble, but because there is always an increase in entropy whenever a substance dissolves, compounds that dissolve endothermically can also be quite soluble.

From another angle:

The formation of a solution is an example of a spontaneous process, a process that occurs under specified conditions without the requirement of energy from some external source. Sometimes we stir a mixture to speed up the dissolution process, but this is not necessary; a homogeneous solution would form if we waited long enough. The topic of spontaneity is critically important to the study of chemical thermodynamics and is treated more thoroughly in a later chapter of this text. For purposes of this module’s discussion, it will suffice to consider two criteria that favor, but do not guarantee, the spontaneous formation of a solution:

  1. A decrease in the internal energy of the system (an exothermic change, as discussed in the future module on thermochemistry)
  2. An increase in the disorder in the system (which indicates an increase in the entropy of the system, as you will learn about in the later chapter on thermodynamics)

Why do some salts dissolve in water while others do not? When a salt is in the solid state, the energy of attraction between cations and anions is called the lattice energy. The lattice energy is described by Coulomb’s law, U  =  constant × [latex]\frac{\text{Q}_{1}\text{Q}_{2}}{\text{d}}[/latex]. When a salt is dissolved in solution, ions are surrounded by water molecules and the energy of attraction between cations and water and between anions and water is called the solvation energy. In order for a salt to dissolve, the ion-ion attractions must be disrupted and new water-ion attractions formed.

The solubility of each salt depends on a comparison of the lattice energy and the solvation energy. For soluble salts, the ion-water attractions (solvation energy) in the solution are greater than the ion-ion attractions (lattice energy) in the solid salt, so the solid dissolves. For insoluble salts, ion-ion attractions (lattice energy) in the solid salt are greater than the ion-water attractions (solvation energy) in the solution, so the solid does not dissolve. For slightly soluble salts, the ion-water attractions (solvation energy) in the solution are approximately equal to the ion-ion attractions (lattice energy) in the solid salt.

Let us consider what happens at the microscopic level when we add solid KCl to water. Ion-dipole forces attract the positive (hydrogen) end of the polar water molecules to the negative chloride ions at the surface of the solid, and they attract the negative (oxygen) end of the polar water molecule to the positive potassium ions. The water molecules penetrate between individual K+ and Cl− ions and surround them, reducing the strong inter-ionic forces that bind the ions together and letting them move off into solution as solvated ions, as Figure 1 shows. The reduction of the electrostatic attraction permits the independent motion of each hydrated ion in a dilute solution, resulting in an increase in the disorder of the system as the ions change from their fixed and ordered positions in the crystal to mobile and much more disordered states in solution. This increased disorder is responsible for the dissolution of many ionic compounds, including KCl, which dissolve with absorption of heat.

In other cases, the electrostatic attractions between the ions in a crystal are so large, or the ion-dipole attractive forces between the ions and water molecules are so weak, that the increase in disorder cannot compensate for the energy required to separate the ions, and the crystal is insoluble. Such is the case for compounds such as calcium carbonate (limestone), calcium phosphate (the inorganic component of bone), and iron oxide (rust).

Precipitation Reactions and Solubility Rules

A precipitation reaction is one in which dissolved substances react to form one (or more) solid products. Many reactions of this type involve the exchange of ions between ionic compounds in aqueous solution and are sometimes referred to as double displacement or double replacement reactions. These reactions are common in nature and are responsible for the formation of coral reefs in ocean waters and kidney stones in animals. They are used widely in industry for production of a number of commodity and specialty chemicals. Precipitation reactions also play a central role in many chemical analysis techniques, including spot tests used to identify metal ions and gravimetric methods for determining the composition of matter.

The extent to which a substance may be dissolved in water, or any solvent, is quantitatively expressed as its solubility, defined as the maximum concentration of a substance that can be achieved under specified conditions. Substances with relatively large solubilities are said to be soluble. A substance will precipitate when solution conditions are such that its concentration exceeds its solubility. Substances with relatively low solubilities are said to be insoluble, and these are the substances that readily precipitate from solution. For purposes of predicting the identities of solids formed by precipitation reactions, one may simply refer to patterns of solubility that have been observed for many ionic compounds (Table 1 and Figure 2).

Soluble compounds contain

  • group 1 metal cations (Li+, Na+, K+, Rb+, and Cs+) and ammonium ion (NH4+)
  • the halide ions (Cl−, Br−, and I−)
  • the acetate (CH3COO−), nitrate (NO3−), chlorate (ClO3−), and perchlorate (ClO4−) ions
  • the sulfate (SO42−) ion
 Exceptions to these solubility rules include

  • halides of Ag+, Hg22+, and Pb2+ are insoluble
  • sulfates of , Ca2+,  Sr2+, Ba2+, and Pb2+ are insoluble
Insoluble compounds contain

  • carbonate (CO32−), chromate (CrO42−), phosphate (PO43−), fluoride (F−), and sulfide (S2−) ions
  • hydroxide ion (OH−)
  Exceptions to these insolubility rules include

  • compounds of these anions with group 1 metal cations and ammonium ion are soluble, plus:
  • magnesium chromate is soluble
  • hydroxides of Sr2+, Ba2+, Ca2+ are slightly soluble
  • sulfides of  Mg2+, Ca2+, Ba2+ are slightly soluble
Table 1. Solubilities of Common Ionic Compounds in Water

 

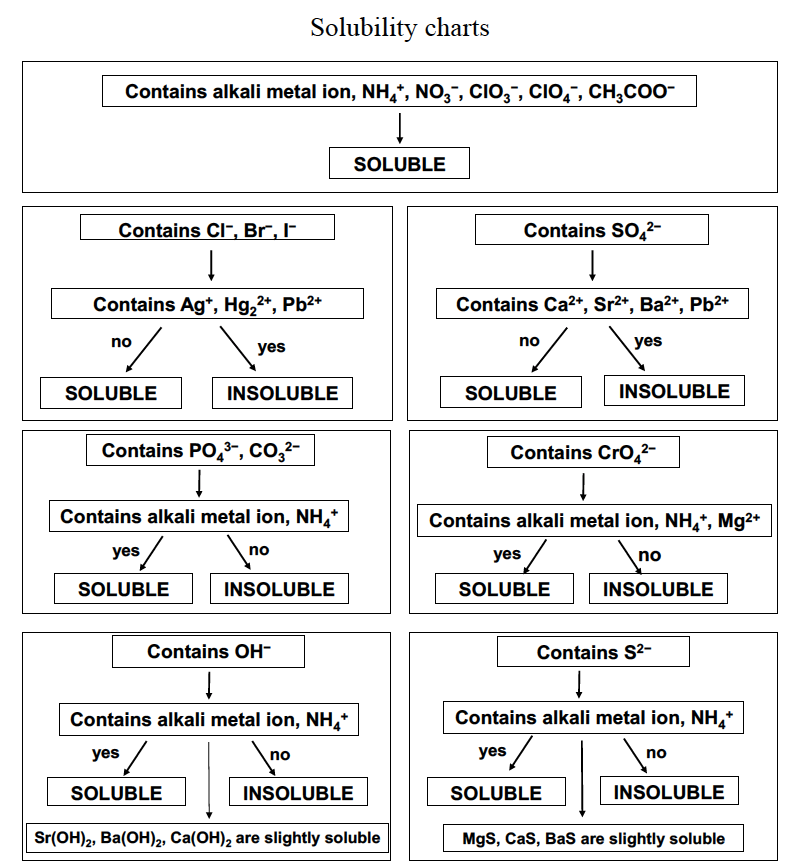
This image is a flow chart describing the general solubility patterns and exceptions.
Figure 3. Solubility Flow Chart

The solubility guidelines in Table 1 and Figure 2 may be used to predict whether a precipitation reaction will occur when solutions of soluble ionic compounds are mixed together. One merely needs to identify all the ions present in the solution and then consider if possible cation/anion pairings could result in an insoluble compound. For example, mixing solutions of silver nitrate and sodium chloride will yield a solution containing Ag+, NO3−, Na+, and Cl− ions. Aside from the two ionic compounds originally present in the solutions, AgNO3 and NaCl, two additional ionic compounds may be derived from this collection of ions: NaNO3 and AgCl. The solubility guidelines indicate all nitrate salts are soluble but that AgCl is one of the exceptions to the general solubility of halide salts. A precipitation reaction, therefore, is predicted to occur, as described by the following equation:

AgNO3(aq)  +  NaCl(aq)   ⟶   AgCl(s)  +  NaNO3(aq)

Overall, Complete Ionic and Net Ionic Equations

Given the abundance of water on earth, it stands to reason that a great many chemical reactions take place in aqueous media. When ions are involved in these reactions, the chemical equations may be written with various levels of detail appropriate to their intended use. To illustrate this, consider a reaction between ionic compounds taking place in an aqueous solution. When aqueous solutions of CaCl2 and AgNO3 are mixed, a reaction takes place producing aqueous Ca(NO3)2 and solid AgCl:

CaCl2(aq)  +  2 AgNO3(aq)   ⟶   Ca(NO3)2(aq)  +  2 AgCl(s)

This balanced equation, derived in the usual fashion, is called an overall equation because it doesn’t explicitly represent the ionic species that are present in solution. When ionic compounds dissolve in water, they may dissociate into their constituent ions, which are subsequently dispersed homogenously throughout the resulting solution. Ionic compounds dissolved in water are, therefore, more realistically represented as dissociated ions. Unlike CaCl2, AgNO3 and Ca(NO3)2, AgCl does not dissolve in water to a significant extent, as signified by its physical state notation, s.

Explicitly representing all dissolved ions results in a complete ionic equation. In this particular case, the formulas for the dissolved ionic compounds are replaced by formulas for their dissociated ions:

Ca2+(aq)  +  2 Cl–(aq)  +  2 Ag+(aq) + 2 NO3–(aq)   ⟶   Ca2+(aq)  +  2 NO3–(aq)  +  2 AgCl(s)

Notice that only the compounds that were represented with “(aq)” dissociated in the complete ionic equation. AgCl(s) remained unchanged since it does not dissociate in solution. Also notice that CaCl2, for example, dissociates into 1 Ca2+ ion and 2 different Cl– ions. The subscript “2” represented that there were 2 Cl atoms for every 1 Ca atom, so when the compound dissociates, 2 Cl– ions are formed.

Examining the above equation shows that two chemical species are present in identical form on both sides of the arrow, Ca2+(aq) and NO3−(aq). These spectator ions—ions whose presence is required to maintain charge neutrality—are neither chemically nor physically changed by the process, and so they may be eliminated from the equation to yield a more succinct representation called a net ionic equation:

2 Cl–(aq)  +  2 Ag+(aq)   ⟶   2 AgCl(s)

Following the convention of using the smallest possible integers as coefficients, this equation is then written:

Cl–(aq)  +  Ag+(aq)   ⟶   AgCl(s)

This net ionic equation indicates that solid silver chloride may be produced from dissolved chloride and silver(I) ions, regardless of the source of these ions. These overall and complete ionic equations provide additional information, namely, the ionic compounds used as sources of Cl− and Ag+.

A vivid example of precipitation is observed when solutions of potassium iodide and lead(II) nitrate are mixed, resulting in the formation of solid lead(II) iodide:

KI(aq)  +  Pb(NO3)2(aq)   ⟶   PbI2(s)  +  2 KNO3(aq)

This observation is consistent with the solubility guidelines: The only insoluble compound among all those involved is lead(II) iodide, one of the exceptions to the general solubility of iodide salts.

Lead(II) iodide is a bright yellow solid that was formerly used as an artist’s pigment known as iodine yellow (Figure 3 and Movie). The properties of pure PbI2 crystals make them useful for fabrication of X-ray and gamma ray detectors.

A photograph is shown of a yellow green opaque substance swirled through a clear, colorless liquid in a test tube.
Figure 3. A precipitate of PbI2 forms when solutions containing Pb2+ and I− are mixed. (credit: Der Kreole/Wikimedia Commons)

Demonstration: Precipitation of lead(II) iodide

Set up. The following video shows the reaction of potassium iodide with lead(II) nitrate. The potassium iodide is in a beaker and the lead(II) nitrate is in the buret. As the lead(II) nitrate is added to the beaker, the reaction will proceed.

Explanation. This video shows the formation of lead(II) iodide as the reaction progresses. Lead(II) iodide is the bright yellow precipitate that forms upon the addition of lead(II) nitrate.

When lead(II) nitrate and potassium iodide are combined, students should be able to write the overall, complete, and net ionic chemical reactions (Figure 4).

When lead(II) nitrate is combined with potassium iodide, lead(II) iodide is formed. Potassium ions and nitrate ions are the spectator ions. This figure writes out the individual chemical equations for the overall, complete, and net ionic equations.
Figure 4. When lead(II) nitrate is combined with potassium iodide, lead(II) iodide is formed. Potassium ions and nitrate ions are the spectator ions.

Example 1

Predicting Precipitation Reactions
Predict the result of mixing reasonably concentrated solutions of the following ionic compounds. If precipitation is expected, write a balanced net ionic equation for the reaction.

(a) potassium sulfate and barium nitrate

(b) lithium chloride and lead(II) acetate

(c) iron(III) nitrate and ammonium carbonate

Solution
(a) The two possible products for this combination are KNO3 and BaSO4. The solubility guidelines indicate BaSO4 is insoluble, and so a precipitation reaction is expected. The net ionic equation for this reaction, derived in the manner detailed in the previous module, is

Ba2+(aq)  +  SO42-(aq)   ⟶   BaSO4(s)

(b) The two possible products for this combination are LiC2H3O2 and PbCl2. The solubility guidelines indicate PbCl2 is insoluble, and so a precipitation reaction is expected. The net ionic equation for this reaction, derived in the manner detailed in the previous module, is

Pb2+(aq)  +  2 Cl–(aq)   ⟶   PbCl2(s)

(c) The two possible products for this combination are Fe2(CO3)3 and NH4NO3. The solubility guidelines indicate Fe2(CO3)3 is insoluble, and so a precipitation reaction is expected. The net ionic equation for this reaction, derived in the manner detailed in the previous module, is

2 Fe3+(aq)  +  3 CO32-(aq)   ⟶   Fe2(CO3)3(s)

Check Your Learning
Which solution could be used to precipitate the barium ion, Ba2+, in a water sample: sodium chloride, sodium hydroxide, or sodium sulfate? What is the formula for the expected precipitate?

Answer:

sodium sulfate; BaSO4

Example 2

Writing Overall and Net Ionic Equations from Descriptions of Chemical Reactions
When carbon dioxide is dissolved in an aqueous solution of sodium hydroxide, the mixture reacts to yield aqueous sodium carbonate and liquid water. Write balanced overall, complete ionic, and net ionic equations for this process.

Solution
Begin by identifying formulas for the reactants and products and arranging them properly in chemical equation form:

CO2(aq)  +  NaOH(aq)   ⟶   Na2CO3(aq)  +  H2O(l)  (unbalanced) 

Balance is achieved easily in this case by changing the coefficient for NaOH to 2, resulting in the overall equation for this reaction:

CO2(aq)  +  2 NaOH(aq)   ⟶   Na2CO3(aq)  +  H2O(l)

The two dissolved ionic compounds, NaOH and Na2CO3, can be represented as dissociated ions to yield the complete ionic equation:

CO2(aq)  +  2 Na+(aq)  +  2 OH–(aq)   ⟶   2 Na+(aq)  +  CO32-(aq)  +  H2O(l)

Finally, identify the spectator ion(s), in this case Na+(aq), and remove it from each side of the equation to generate the net ionic equation:

CO2(aq)  +  2 OH–(aq)   ⟶   CO32-(aq)  +  H2O(l)

Check Your Learning
Diatomic chlorine and sodium hydroxide (lye) are commodity chemicals produced in large quantities, along with diatomic hydrogen, via the electrolysis of brine, according to the following unbalanced equation:

NaCl(aq)  +  H2O(l)   ⟶   NaOH(aq)  +  H2(g)  +  Cl2(g)

Write balanced overall, complete ionic, and net ionic equations for this process.

Answer:

balanced overall: 2 NaCl(aq)  +  2 H2O(l)   ⟶   2 NaOH(aq)  +  H2(g)  +  Cl2(g)

complete ionic: 2 Na+(aq)  +  2 Cl–(aq)  +  2 H2O(l)   ⟶   2 Na+(aq)  +  2 OH–(aq)  +  H2(g)  +  Cl2(g)

net ionic: 2 Cl–(aq)  +  2 H2O(l)   ⟶   2 OH–(aq)  +  H2(g)  +  Cl2(g)

Key Concepts and Summary

The solubility of each salt depends on a comparison of the lattice energy and the solvation energy. For soluble salts, the ion-water attractions (solvation energy) in the solution are greater than the ion-ion attractions (lattice energy) in the solid salt, so the solid dissolves. For insoluble salts, ion-ion attractions (lattice energy) in the solid salt are greater than the ion-water attractions (solvation energy) in the solution, so the solid does not dissolve. For slightly soluble salts, the ion-water attractions (solvation energy) in the solution are approximately equal to the ion-ion attractions (lattice energy) in the solid salt.

Chemical reactions in aqueous solution that involve ionic reactants or products may be represented more realistically by complete ionic equations and more succinctly by net ionic equations. Complete ionic equations represent all aqueous compounds as dissociated ions in solution, while any compound that is solid, liquid, or gas remains intact. Spectator ions are ions that do not participate in the reaction since they appear the exact same (same charge and same phase) on both sides of the reaction. These ions are removed for the net ionic reaction.

Glossary

complete ionic equation
chemical equation in which all dissolved ionic reactants and products, including spectator ions, are explicitly represented by formulas for their dissociated ions
net ionic equation
chemical equation in which only those dissolved ionic reactants and products that undergo a chemical or physical change are represented (excludes spectator ions)
spectator ion
ion that does not undergo a chemical or physical change during a reaction, but its presence is required to maintain charge neutrality

Chemistry End of Section Exercises

  1. What is the expected electrical conductivity of the following solutions?
    1. NaOH(aq)
    2. HCl(aq)
    3. C6H12O6(aq) (glucose)
    4. NH3(l)
  2. Write the overall, total ionic, and net ionic equations for the following reactions:
    1. Ca(OH)2  +  HC2H3O2(aq)  ⟶
    2. H3PO4(aq)  +  CaCl2(aq)  ⟶
  3. From the balanced overall equations, write the complete ionic and net ionic equations for the following:
    1. K2C2O4(aq)  +  Ba(OH)2(aq)  ⟶  KOH(aq)  +  BaC2O4(s)
    2. Pb(NO3)2(aq)  +  Na2SO4(aq)  ⟶  PbSO4(s)  +  NaNO3(aq)

Answers to Chemistry End of Section Exercises

  1. (a) high conductivity (solute is an ionic compound that will dissociate when dissolved);
    (b) high conductivity (solute is a strong acid and will ionize completely when dissolved);
    (c) nonconductive (solute is a covalent compound, neither acid nor base, unreactive towards water);
    (d) low conductivity (solute is a weak base and will partially ionize when dissolved)
  2. (a) Overall: Ca(OH)2(aq) + 2 HC2H3O2(aq) → Ca(C2H3O2)2(aq) + 2 H2O(l)
    Total ionic: Ca2+(aq) + 2 OH–(aq) + 2 HC2H3O2(aq) → Ca2+(aq) + 2 C2H3O2–(aq) + 2 H2O(l)
    Net ionic: 2 OH–(aq) + 2 HC2H3O2(aq) → 2 C2H3O2–(aq) + 2 H2O(l)
    (b) Overall: 2 H3PO4(aq) + 3 CaCl2(aq) → Ca3(PO4)2(s) + 6 HCl(aq);
    Total ionic: 6 H+(aq) + 2 PO43-(aq) + 3 Ca2+(aq) + 6 Cl–(aq) → Ca3(PO4)2(s) + 6 HCl(aq)
    Net ionic: 2 PO43-(aq) + 3 Ca2+(aq) → Ca3(PO4)2(s)
  3. (a) Overall:  K2C2O4(aq)  +  Ba(OH)2(aq)  ⟶  2 KOH(aq)  +  BaC2O4(s)
    Total ionic:  2 K+(aq)  +  C2O42-(aq)  +  Ba2+  +  2 OH-(aq)  ⟶  2 K+(aq)  +  2 OH–(aq)  +  BaC2O4(s)
    Net ionic:  C2O42-(aq)  +  Ba2+  ⟶  BaC2O4(s)
    (b) Overall:  Pb(NO3)2(aq)  +  Na2SO4(aq)  ⟶  PbSO4(s)  +  2 NaNO3(aq)
    Total ionic:  Pb2+(aq)  +  2 NO3–(aq)  +  2 Na+(aq)  +  SO4–(aq)  ⟶  PbSO4(s)  +  2 NaNO3(aq)
    Net ionic:  Pb2+(aq)  +  SO4–(aq)  ⟶  PbSO4(s)

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

UW-Madison Chemistry 103/104 Resource Book Copyright © by crlandis is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book