61 Types of Unit Cells: Body-Centered Cubic and Face-Centered Cubic (M11Q5)
Introduction
In the previous section, we identified that unit cells were the simplest repeating unit of a crystalline solid and examined the most basic unit cell, the primitive cubic unit cell. In this section, we continue by looking at two other unit cell types, the body-centered cubic and the face-centered cubic unit cells.
Learning Objectives for Types of Unit Cells: Body-Centered Cubic and Face-Centered Cubic Cells
- Identify what defines a unit cell; distinguish between the three common cubic unit cell types and their characteristics.
| Body-Centered Cubic Cells | Face-Centered Cubic Cells | Summary of Cubic Unit Cells |
| Key Concepts and Summary | Glossary | End of Section Exercises |
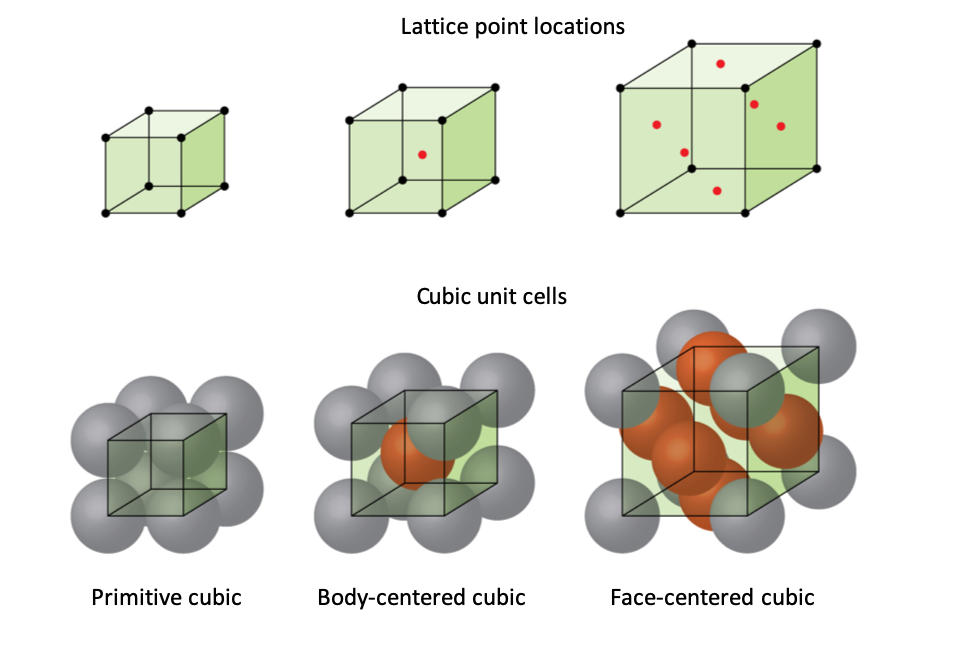
We will focus on the three basic cubic unit cells: primitive cubic (from the previous section), body-centered cubic unit cell, and face-centered cubic unit cell—all of which are illustrated in Figure 1.
Body-Centered Cubic Cells
Some metals crystallize in an arrangement that has a cubic unit cell with atoms at all of the corners and an atom in the center, as shown in Figure 2. This is called a body-centered cubic (BCC) solid. Atoms in the corners of a BCC unit cell do not contact each other but contact the atom in the center. A BCC unit cell contains two atoms: one-eighth of an atom at each of the eight corners (8 × [latex]\frac{1}{8}[/latex] = 1 atom from the corners) plus one atom from the center. Any atom in this structure touches four atoms in the layer above it and four atoms in the layer below it. Thus, an atom in a BCC structure has a coordination number of eight.
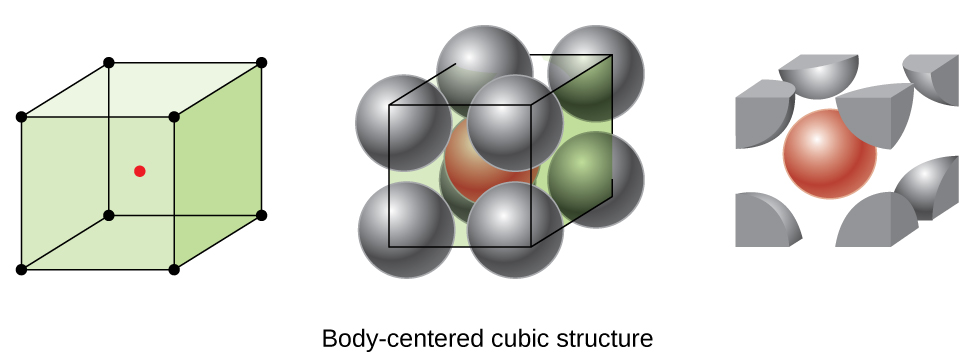
Atoms in BCC arrangements are much more efficiently packed than in a simple cubic structure, occupying about 68% of the total volume. Isomorphous metals with a BCC structure include K, Ba, Cr, Mo, W, and Fe at room temperature. (Elements or compounds that crystallize with the same structure are said to be isomorphous.)
Face-Centered Cubic Cells
Many other metals, such as aluminum, copper, and lead, crystallize in an arrangement that has a cubic unit cell with atoms at all of the corners and at the centers of each face, as illustrated in Figure 3. This arrangement is called a face-centered cubic (FCC) solid. A FCC unit cell contains four atoms: one-eighth of an atom at each of the eight corners (8 × [latex]\frac{1}{8}[/latex] = 1 atom from the corners)) and one-half of an atom on each of the six faces (6 × [latex]\frac{1}{2}[/latex] = 3 atoms from the corners) atoms from the faces). The atoms at the corners touch the atoms in the centers of the adjacent faces along the face diagonals of the cube. Because the atoms are on identical lattice points, they have identical environments.
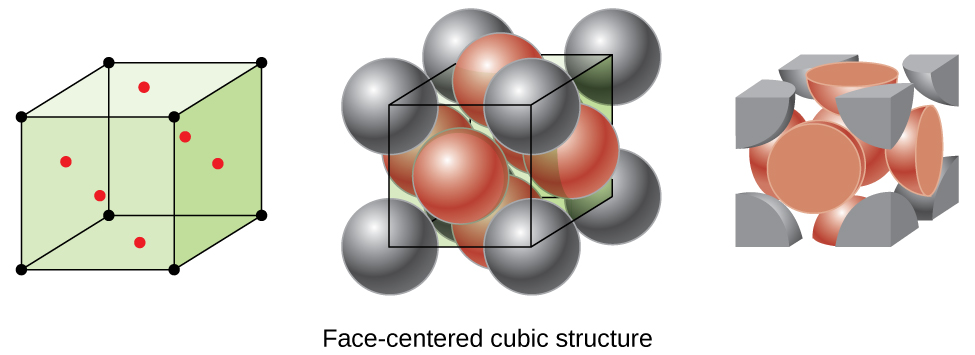
Atoms in an FCC arrangement are packed as closely together as possible, with atoms occupying 74% of the volume. This structure is also called cubic closest packing (CCP). In CCP, there are three repeating layers of hexagonally arranged atoms. Each atom contacts six atoms in its own layer, three in the layer above, and three in the layer below. In this arrangement, each atom touches 12 near neighbors, and therefore has a coordination number of 12. The fact that FCC and CCP arrangements are equivalent may not be immediately obvious, but why they are actually the same structure is illustrated in Figure 4.
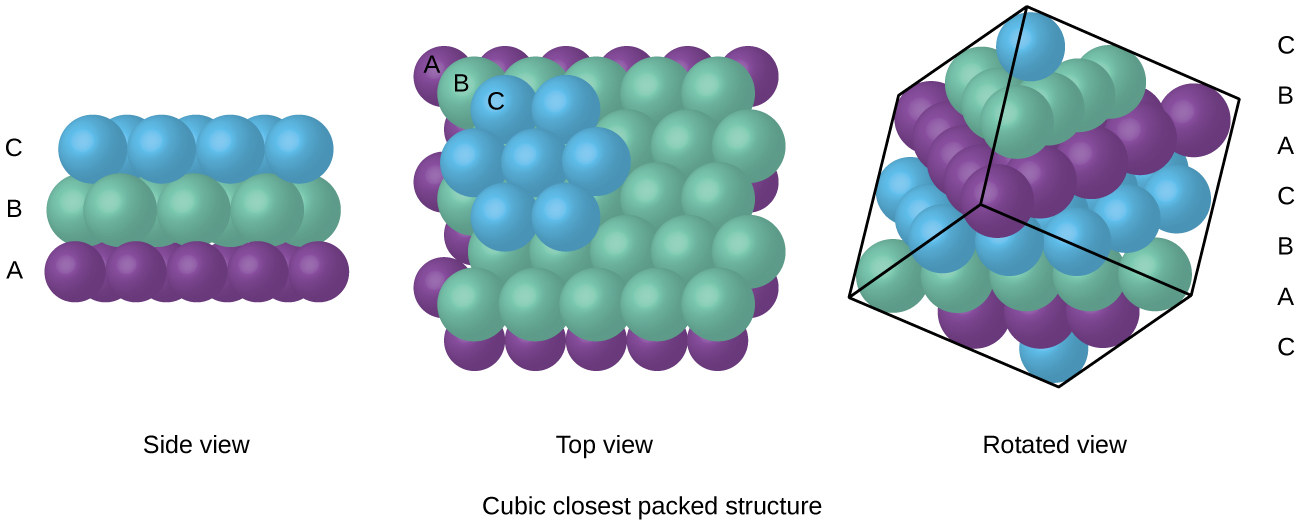
Because closer packing maximizes the overall attractions between atoms and minimizes the total intermolecular energy, the atoms in most metals pack in this manner.
Example 1
Calculation of Atomic Radius and Density for Metals, Part 2
Calcium crystallizes in a face-centered cubic structure. The edge length of its unit cell is 558.8 pm.
(a) What is the atomic radius of Ca in this structure?
(b) Calculate the density of Ca.
Solution
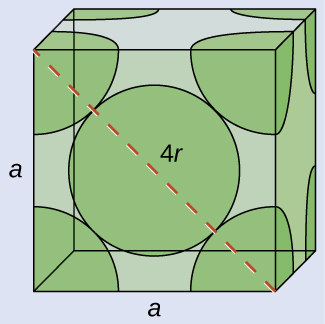
(a) In an FCC structure, Ca atoms contact each other across the diagonal of the face, so the length of the diagonal is equal to four Ca atomic radii (d = 4r). Two adjacent edges and the diagonal of the face form a right triangle, with the length of each side equal to 558.8 pm and the length of the hypotenuse equal to four Ca atomic radii:
Solving this gives r = [latex]{\frac{(558.8\;\text{pm})^2\;+\;(558.5\;\text{pm})^2}{16}}[/latex] = 197.6 pm fro a Ca radius.
(b) Density is given by density = [latex]\frac{\text{mass}}{\text{volume}}[/latex]. The density of calcium can be found by determining the density of its unit cell: for example, the mass contained within a unit cell divided by the volume of the unit cell. A face-centered Ca unit cell has one-eighth of an atom at each of the eight corners (8 × [latex]\frac{1}{8}[/latex] = 1atom) and one-half of an atom on each of the six faces (6 × [latex]\frac{1}{2}[/latex] = 3), for a total of four atoms in the unit cell.
The mass of the unit cell can be found by:
The volume of a Ca unit cell can be found by:
(Note that the edge length was converted from pm to cm to get the usual volume units for density.)
Then, the density of Ca = [latex]\frac{2.662\;\times\;10^{-22}\;\text{g}}{1.745\;\times\;10^{-22}\;\text{cm}^{3}}[/latex] = 1.53 g/cm3
Check Your Learning
Silver crystallizes in an FCC structure. The edge length of its unit cell is 409 pm.
(a) What is the atomic radius of Ag in this structure?
(b) Calculate the density of Ag.
Answer:
(a) 145 pm; (b) 10.5 g/cm3
Summary of Cubic Unit Cells
| Primitive Cubic (PC) | Body-Centered Cubic (BCC) | Face-Centered Cubic (FCC) | |
| Atoms per unit cell | 1 | 2 | 4 |
| Coordination number | 6 | 8 | 12 |
| Atom radius (r) and cell length (l) | 2r = l | [latex]\sqrt{3}[/latex] × l = 4r | [latex]\sqrt{2}[/latex] × l = 4r |
| Packing efficiency | 52 % | 68 % | 74 % |
Key Concepts and Summary
The structures of crystalline metals and simple ionic compounds can be described in terms of packing of spheres. Metal atoms can pack in primitive cubic, body-centered cubic, and face-centered cubic structures. Each packing has its own characteristics with respect to the volume occupied by the atoms and the closeness of the packing.
Glossary
- body-centered cubic (BCC) solid
- crystalline structure that has a cubic unit cell with lattice points at the corners and in the center of the cell
- body-centered cubic unit cell
- simplest repeating unit of a body-centered cubic crystal; it is a cube containing lattice points at each corner and in the center of the cube
- cubic closest packing (CCP)
- crystalline structure in which planes of closely packed atoms or ions are stacked as a series of three alternating layers of different relative orientations (ABC)
- face-centered cubic (FCC) solid
- crystalline structure consisting of a cubic unit cell with lattice points on the corners and in the center of each face
- face-centered cubic unit cell
- simplest repeating unit of a face-centered cubic crystal; it is a cube containing lattice points at each corner and in the center of each face
- isomorphous
- possessing the same crystalline structure
Chemistry End of Section Exercises
- What is the coordination number of a chromium atom in the body-centered cubic structure of chromium?
- What is the coordination number of an aluminum atom in the face-centered cubic structure of aluminum?
- Tungsten crystallizes in a body-centered cubic unit cell with an edge length of 3.165 Å.
- What is the atomic radius of tungsten in this structure?
- Calculate the density of tungsten.
- Platinum (atomic radius = 1.38 Å) crystallizes in a cubic closely packed structure. Calculate the edge length of the face-centered cubic unit cell and the density of platinum.
- Barium crystallizes in a body-centered cubic unit cell with an edge length of 5.025 Å
- What is the atomic radius of barium in this structure?
- Calculate the density of barium.
- Aluminum (atomic radius = 1.43 Å) crystallizes in a cubic closely packed structure. Calculate the edge length of the face-centered cubic unit cell and the density of aluminum.
Answers to Chemistry End of Section Exercises
- eight
- twelve
- (a) 1.370 Å; (b) 19.26 g/cm3
- edge length: 3.903 Å; density: 21.79 g/cm3
- (a) 2.176 Å; (b) 3.595 g/cm3
- edge length: 4.045 Å; density: 2.709 g/cm3

