20 Pressure and Ideal Gas Laws (M5Q1)

Introduction

This section explores atmospheric pressure and the scientific laws which describe relationships between macroscopic physical properties of gases: pressure, volume, temperature, and amount of gas. These laws are combined in the ideal gas law, which is applicable to gases under conditions of relatively low pressure and high temperature. Understanding the fundamental relationships between pressure, temperature, volume, and moles of gas in the ideal gas law is a central goal for this course and will be further explored throughout this module. This section includes worked examples, sample problems, and a glossary. 

Learning Objectives for Pressure and the Ideal Gas Law

| Key Concepts and Summary | Key Equations | Glossary | End of Section Exercises |

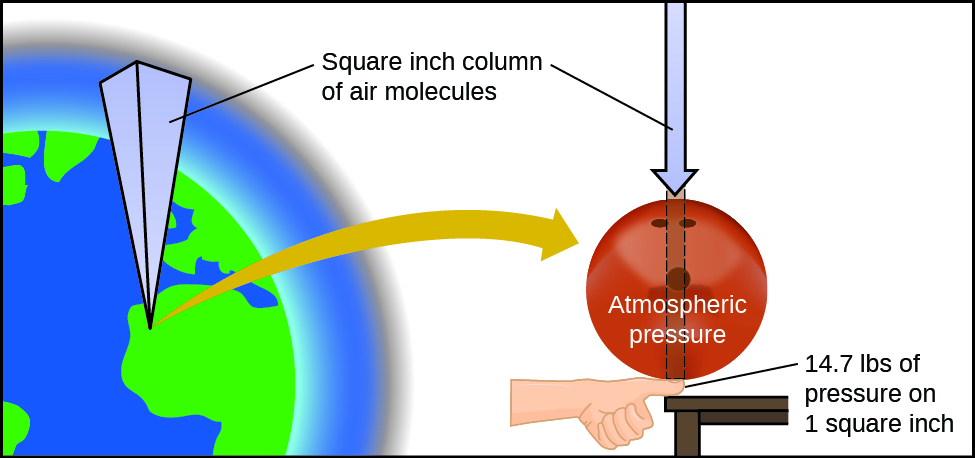
The earth’s atmosphere exerts a pressure, as does any other gas. Although we do not normally notice atmospheric pressure, we are sensitive to pressure changes—for example, when your ears “pop” during take-off and landing while flying, or when you dive underwater. Gas pressure is caused by the force exerted by gas molecules colliding with the surfaces of objects (Figure 1). Although the force of each collision is very small, any surface of appreciable area experiences a large number of collisions in a short time, which can result in a high pressure. In fact, normal air pressure is strong enough to crush a metal container when not balanced by equal pressure from inside the container.

The left side of this figure includes a graphic of the earth with an inverted rectangular prism extending from a point on it. Near the top of the image, the label, “square inch column of air molecules” is connected to the prism with a line segment. This label is also connected with a line segment to a downward pointing arrow at the right side of the figure. Beneath the arrow is a red circle labeled, “atmospheric pressure.” A narrow rectangle with a dashed line border extends from the bottom of the arrow vertically through the circle. Directly beneath this rectangle at the lower edge of the circle is a hand with a thumb appearing to be resting on a tabletop. The thumb is connected with a line segment to the label, “14.7 lbs of pressure on 1 square inch.” The red circle is sitting on top of the thumb.
Figure 1. The atmosphere above us exerts a large pressure on objects at the surface of the earth, roughly equal to the weight of a bowling ball pressing on an area the size of a human thumbnail.

 

A dramatic illustration of atmospheric pressure is provided in this brief video, which shows a railway tanker car imploding when its internal pressure is decreased.

A smaller scale demonstration of this phenomenon is briefly explained.

Pressure and Atmospheric Pressure

Atmospheric pressure is caused by the weight of the column of air molecules in the atmosphere above an object. At sea level, this pressure is roughly the same as that exerted by a full-grown African elephant standing on a doormat, or a typical bowling ball resting on your thumbnail. These may seem like huge amounts, and they are, but life on earth has evolved under such atmospheric pressure. If you actually perch a bowling ball on your thumbnail, the pressure experienced is twice the usual pressure, and the sensation is unpleasant.

Demonstration: Effect of atmospheric pressure

Set up. The effect of atmospheric pressure can be seen in the following two videos. In the first video, you will see the effect of atmospheric pressure on a soda can. Before the video was recorded, a small amount of water was put into the soda can and then boiled. After boiling the water for a while, the video begins. You can see the water vapor (steam) coming out of the can at the beginning of the video. Then the can is inverted in a cold water bath.

Explanation. The can was crushed by the atmospheric pressure. Usually, a can is not susceptible to the atmospheric pressure in this way because the pressure inside the open can is equal to the pressure outside the open can. But when the can was heated and the water inside was boiled, the vapor from the boiling water pushed air out of the can. After suddenly cooling the water vapor inside the can by inverting it into a cold water bath, the water vapor condensed and a partial vacuum was formed. The atmospheric pressure outside the can was greater than the pressure inside the can, and the can was crushed because the aluminum could not withstand the atmospheric pressure.

In the next video, the experiment is scaled up considerably and performed on a tanker. In this video, instead of heating the tanker car to drive out the air, a vacuum pump was used to pump out the air molecules. Before this particular part of the video, the team pumped air from the intact tanker car and the car did not collapse. Even though the atmospheric pressure outside the tanker car was greater than the pressure inside the tanker car, the walls of the tanker are strong enough to withstand this pressure difference (something the aluminum can above was not capable of). In this section of the video, the team disrupts the integrity of the structure by making a dent in the tanker before pulling a vacuum.

Explanation. You can see that the atmospheric pressure is even strong enough to crush a tanker car (provided the tanker car is already damaged in some way). This is the pressure that we are accustomed to living under every day, but these videos demonstrate how much pressure this really is.

In general, pressure is defined as the force exerted on a given area: P  =  [latex]\frac{\text{F}}{\text{A}}[/latex]. Note that pressure is directly proportional to force and inversely proportional to area. Thus, pressure can be increased either by increasing the amount of force or by decreasing the area over which it is applied; pressure can be decreased by decreasing the force or increasing the area.

Let’s apply this concept to determine which would be more likely to fall through thin ice in Figure 2—the elephant or the figure skater? A large African elephant can weigh 7 tons, supported on four feet, each with a diameter of about 1.5 ft (footprint area of 250 in2), so the pressure exerted by each foot is about 14 lb/in2:

1 ton  =  2,000 lbs

pressure per elephant foot  =  [latex]\frac{\text{14,000 lbs}}{\text{elephant}}[/latex] × [latex]\frac{1 \;\text{elephant}}{4 \;\text{feet}}[/latex] × [latex]\frac{1 \;\text{foot}}{250 \;\text{in}^2}[/latex]  =  14 lb/in2

The figure skater weighs about 120 lbs, supported on two skate blades, each with an area of about 2 in2, so the pressure exerted by each blade is about 30 lb/in2:

pressure per elephant foot  =  [latex]\frac{\text{120 lbs}}{\text{skater}}[/latex] × [latex]\frac{1 \;\text{skater}}{2 \;\text{blades}}[/latex] × [latex]\frac{1 \;\text{blade}}{2 \;\text{in}^2}[/latex]  =  30 lb/in2

Even though the elephant is more than one hundred-times heavier than the skater, it exerts less than one-half of the pressure and would therefore be less likely to fall through thin ice. On the other hand, if the skater removes her skates and stands with bare feet (or regular footwear) on the ice, the larger area over which her weight is applied greatly reduces the pressure exerted:

pressure per human foot  =  [latex]\frac{\text{120 lbs}}{\text{skater}}[/latex] × [latex]\frac{1 \;\text{skater}}{2 \;\text{feet}}[/latex] × [latex]\frac{1 \;\text{foot}}{30 \;\text{in}^2}[/latex]  =  2 lb/in2

This figure includes two photographs. Figure a is a photo of a large gray elephant on grassy, beige terrain. Figure b is a photo of a figure skater with her right skate on the ice, upper torso lowered, arms extended upward behind her chest, and left leg extended upward behind her.
Figure 2. Although (a) an elephant’s weight is large, creating a very large force on the ground, (b) the figure skater exerts a much higher pressure on the ice due to the small surface area of her skates. (credit a: modification of work by Guido da Rozze; credit b: modification of work by Ryosuke Yagi)

The SI unit of pressure is the pascal (Pa), with 1 Pa  =  1 N/m2, where N is a newton, a unit of force defined as 1 kg·m/s2. One pascal is a small pressure which is why it is more convenient to use units of kilopascal (1 kPa  =  1000 Pa) or bar (1 bar  =  100,000 Pa). In the United States, pressure is often measured in pounds of force on an area of one square inch—pounds per square inch (psi)—for example, in car tires. Pressure can also be measured using the unit atmosphere (atm), which originally represented the average sea level air pressure at the approximate latitude of Paris (45°). Table 1 below provides some information on these and a few other common units for pressure measurements.

Unit name and abbreviation Definition or relation to other unit(s)
pascal (Pa) 1 Pa  =  1 N/m2
kilopascal (kPa) 1 kPa  =  1000 Pa (recommended IUPAC unit)
pounds per square inch (psi) air pressure at sea level is ~14.7 psi
atmosphere (atm) 1 atm  =  101,325 Pa (air pressure at sea level is ~1 atm)
bar (bar, or b) 1 bar  =  100,000 Pa
millibar (mbar, or mb) 1000 mbar  =  1 bar
inches of mercury (in. Hg) 1 in. Hg  =  3386 Pa
torr 760 torr  =  1 atm
millimeters of mercury (mm Hg) 1 mmHg  ~  1 torr
Table I. Units of Pressure.

Example 1

Conversion of Pressure Units
The United States National Weather Service reports pressure in both inches of Hg and millibars. Convert a pressure of 29.2 in. Hg into:

(a) torr

(b) atm

(c) kPa

(d) mbar

Solution
This is a unit conversion problem. The relationships between the various pressure units are given in Table 1.

(a) 29 in Hg × [latex]\frac{25.4 \;\rule[0.25ex]{1.2em}{0.1ex}\hspace{-1.2em}\text{mm}}{1 \;\rule[0.25ex]{0.6em}{0.1ex}\hspace{-0.6em}\text{in}}[/latex] × [latex]\frac{1 \;\text{torr}}{1 \;\rule[0.25ex]{2em}{0.1ex}\hspace{-2em}\text{mm Hg}}[/latex]  =  742 torr

(b) 742 torr × [latex]\frac{1 \;\text{atm}}{760 \;\rule[0.25ex]{1.2em}{0.1ex}\hspace{-1.2em}\text{torr}}[/latex]  =  0.976 atm

(c) 742 torr × [latex]\frac{101.325 \;\text{kPa}}{760 \;\rule[0.25ex]{1.0em}{0.1ex}\hspace{-1.0em}\text{torr}}[/latex]  =  98.9 kPa

(d) 98.9 kPa × [latex]\frac{1000 \;\rule[0.25ex]{0.9em}{0.1ex}\hspace{-0.9em}\text{Pa}}{1 \;\rule[0.25ex]{1.1em}{0.1ex}\hspace{-1.1em}\text{kPa}}[/latex] × [latex]\frac{1 \;\rule[0.25ex]{0.9em}{0.1ex}\hspace{-0.9em}\text{bar}}{100,000 \;\rule[0.25ex]{1.0em}{0.1ex}\hspace{-1.0em}\text{Pa}}[/latex] × [latex]\frac{1000 \;\text{mbar}}{1 \;\rule[0.25ex]{1.0em}{0.1ex}\hspace{-1.0em}\text{bar}}[/latex]  =  989 mbar

Check Your Learning
A typical barometric pressure in Kansas City is 740 torr. What is this pressure in atmospheres (atm), in millimeters of mercury (mm Hg), in kilopascals (kPa), and in bar?

Answer:

0.974 atm; 740 mm Hg; 98.7 kPa; 0.987 bar

Measuring Pressure

We can measure atmospheric pressure, the force exerted by the atmosphere on the earth’s surface, with a barometer (Figure 3). A barometer is a glass tube that is closed at one end, filled with a nonvolatile liquid such as mercury, and then inverted and immersed in a container of that liquid. The atmosphere exerts pressure on the liquid outside the tube, the weight of the column of liquid exerts pressure inside the tube, and the pressure at the liquid surface is the same inside and outside the tube. The height of the liquid in the tube is therefore proportional to the pressure exerted by the atmosphere.

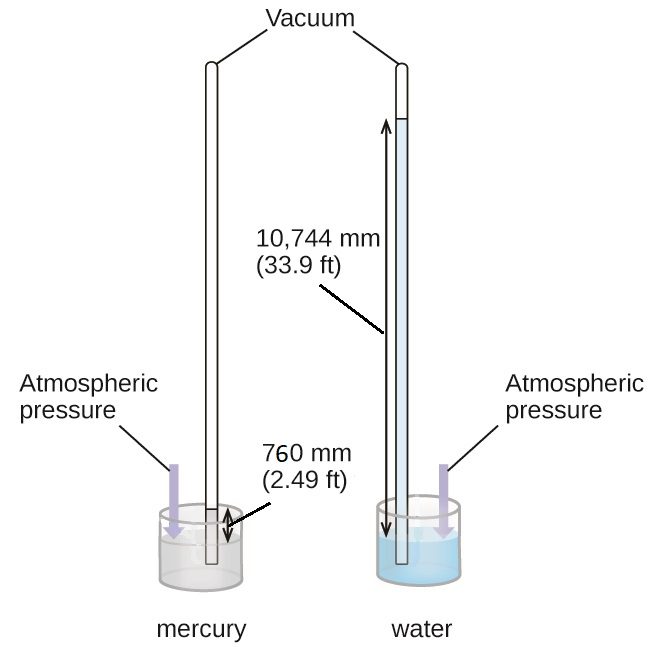
Figure 3. In a barometer, the height, h, of the column of liquid is used as a measurement of the air pressure. Using very dense liquid mercury (left) permits the construction of reasonably sized barometers, whereas using water (right) would require a barometer more than 30 feet tall.

If the liquid is water, normal atmospheric pressure will support a column of water over 10 meters high, which is rather inconvenient for making (and reading) a barometer. Because mercury (Hg) is about 13.6-times denser than water, a mercury barometer only needs to be [latex]\frac{1}{13.6}[/latex] as tall as a water barometer—a more suitable size. Standard atmospheric pressure of 1 atm at sea level (101,325 Pa) corresponds to a column of mercury that is about 760 mm (29.92 in.) high.

Chemistry in Real Life: Measuring Blood Pressure

Blood pressure is measured using a device called a sphygmomanometer (Greek sphygmos  =  “pulse”). It consists of an inflatable cuff to restrict blood flow, a manometer to measure the pressure, and a method of determining when blood flow begins and when it becomes impeded (Figure 4). Since its invention in 1881, it has been an essential medical device. There are many types of sphygmomanometers: manual ones that require a stethoscope and are used by medical professionals, mercury ones used when the most accuracy is required, less accurate mechanical ones, and digital ones that can be used with little training but that have limitations. When using a sphygmomanometer, the cuff is placed around the upper arm and inflated until blood flow is completely blocked, then slowly released. As the heart beats, blood forced through the arteries causes a rise in pressure. This rise in pressure at which blood flow begins is the systolic pressure—the peak pressure in the cardiac cycle. When the cuff’s pressure equals the arterial systolic pressure, blood flows past the cuff, creating audible sounds that can be heard using a stethoscope. This is followed by a decrease in pressure as the heart’s ventricles prepare for another beat. As cuff pressure continues to decrease, eventually sound is no longer heard; this is the diastolic pressure—the lowest pressure (resting phase) in the cardiac cycle. Blood pressure units from a sphygmomanometer are in terms of millimeters of mercury (mm Hg).

This figure includes two photographs. The first photo shows a young adult male placing a blood pressure cuff on the upper arm of a young adult female. The second image shows a typical sphygmomanometer, which includes a black blood pressure cuff, tubing, pump, and pressure gauge.
Figure 4. (a) A medical technician prepares to measure a patient’s blood pressure with a sphygmomanometer. (b) A typical sphygmomanometer uses a valved rubber bulb to inflate the cuff and a diaphragm gauge to measure pressure. (credit a: modification of work by Master Sgt. Jeffrey Allen)

Chemistry in Real Life: Meteorology, Climatology, and Atmospheric Science

Throughout the ages, people have observed clouds, winds, and precipitation, trying to discern patterns and make predictions, including when it is best to plant and harvest, whether it is safe to set out on a sea voyage, and much more. We now face complex weather and atmosphere-related changes and challenges that will have a major impact on our civilization and the ecosystem. Several different scientific disciplines use chemical principles to help us better understand weather, the atmosphere, and climate. These are meteorology, climatology, and atmospheric science. Meteorology is the study of the atmosphere, atmospheric phenomena, and atmospheric effects on earth’s weather. Meteorologists seek to understand and predict the weather in the short term, which can save lives and benefit the economy. Weather forecasts (Figure 5) are the result of thousands of measurements of air pressure, temperature, and the like, which are compiled, modeled, and analyzed in weather centers worldwide.

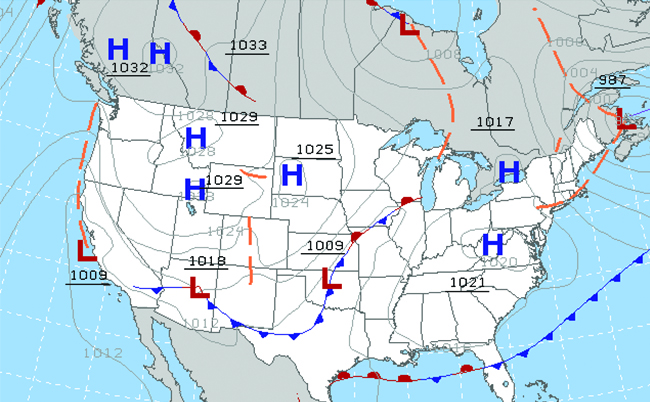
A weather map of the United States is shown which points out areas of high and low pressure with the letters H in blue and L in red. Curved lines in grey, orange, blue, and red are shown. The orange lines are segmented. The red and blue lines have small red or blue semi-circles and triangles attached along their lengths. In dashed white lines, latitude and longitude are indicated. Underlined three and four digit numbers also appear across the map.
Figure 5. Meteorologists use weather maps to describe and predict weather. Regions of high (H) and low (L) pressure have large effects on weather conditions. The gray lines represent locations of constant pressure known as isobars. (credit: modification of work by National Oceanic and Atmospheric Administration)

In terms of weather, low-pressure systems occur when the earth’s surface atmospheric pressure is lower than the surrounding environment: Moist air rises and condenses, producing clouds. Movement of moisture and air within various weather fronts instigates most weather events.

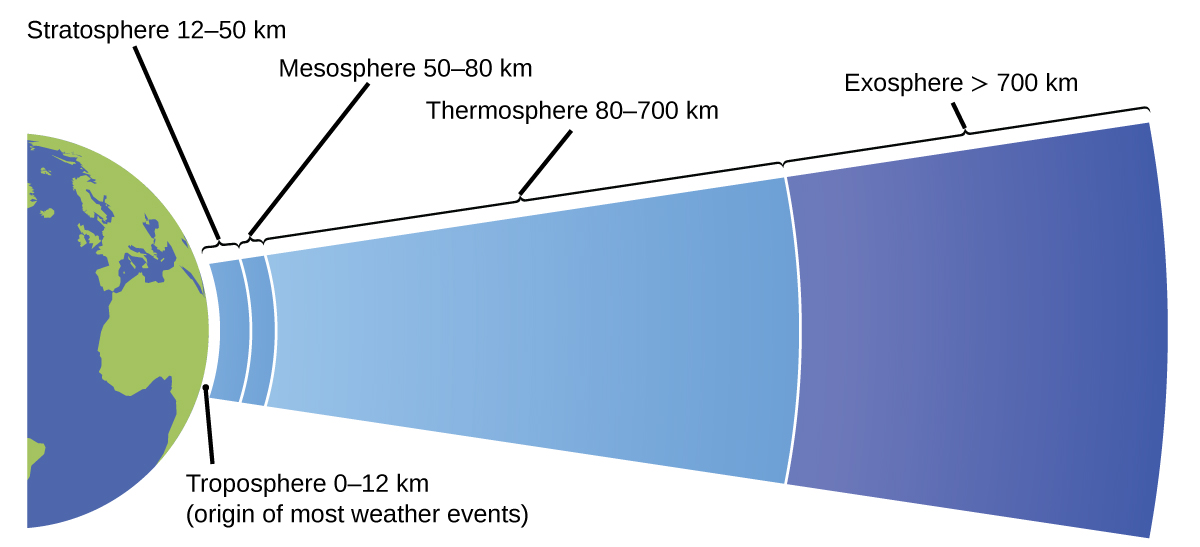
The atmosphere is the gaseous layer that surrounds a planet. Earth’s atmosphere, which is roughly 100–125 km thick, consists of roughly 78.1% nitrogen and 21.0% oxygen, and can be subdivided further into the regions shown in Figure 6: the exosphere (furthest from earth, > 700 km above sea level), the thermosphere (80–700 km), the mesosphere (50–80 km), the stratosphere (second lowest level of our atmosphere, 12–50 km above sea level), and the troposphere (up to 12 km above sea level, roughly 80% of the earth’s atmosphere by mass and the layer where most weather events originate). As you go higher in the troposphere, air density and temperature both decrease.

This diagram shows half of a two dimensional view of the earth in blue and green. A narrow white layer, labeled “troposphere 0 dash 12 k m” covers this hemisphere. This layer is also labeled “layer where most weather events originate.” Next, a thicker light blue layer labeled “Stratosphere 12 dash 50 k m” is shown. This is followed by a slightly thinner layer also in light blue labeled “Mesosphere 50 dash 80 k m.” Following this layer is a relatively thick light blue layer labeled “Thermosphere 80 dash 700 k m.” A blue layer appears that covers the rightmost two thirds of the diagram. This region gradually darkens from a lighter blue at the left to a dark blue at the right. This region of the diagram is labeled “exosphere greater than 700 k m.”
Figure 6. Earth’s atmosphere has five layers: the troposphere, the stratosphere, the mesosphere, the thermosphere, and the exosphere.

Climatology is the study of the climate: averaged weather conditions over long time periods, using atmospheric data. In comparison to meteorologists who study weather in weeks, days, and hours, climatologists study patterns and effects that occur over decades, centuries, and millennia. Atmospheric science is a broad field, combining meteorology, climatology, and other scientific disciplines that study the atmosphere.

During the seventeenth and especially eighteenth centuries, driven both by a desire to understand nature and a quest to make balloons in which they could fly (Figure 7), a number of scientists established the relationships between the macroscopic physical properties of gases: pressure, volume, temperature, and amount of gas. Although their measurements were not precise by today’s standards, they were able to determine the mathematical relationships between pairs of these variables (e.g., pressure and temperature, pressure and volume) that hold for an ideal gas—a hypothetical construct that real gases approximate under certain conditions. Eventually, these individual laws were combined into a single equation—the ideal gas law—that relates gas quantities for gases and is quite accurate for low pressures and moderate temperatures. We will consider the key developments in individual relationships (for pedagogical reasons not quite in historical order), then put them together in the ideal gas law.

This figure includes three images. Image a is a black and white image of a hydrogen balloon apparently being deflated by a mob of people. In image b, a blue, gold, and red balloon is being held to the ground with ropes while positioned above a platform from which smoke is rising beneath the balloon. In c, an image is shown in grey on a peach-colored background of an inflated balloon with vertical striping in the air. It appears to have a basket attached to its lower side. A large stately building appears in the background.
Figure 7. In 1783, the first (a) hydrogen-filled balloon flight, (b) manned hot air balloon flight, and (c) manned hydrogen-filled balloon flight occurred. When the hydrogen-filled balloon depicted in (a) landed, the frightened villagers of Gonesse reportedly destroyed it with pitchforks and knives. The launch of the latter was reportedly viewed by 400,000 people in Paris.

Pressure and Temperature Relationship for Ideal Gases

Imagine filling a rigid container attached to a pressure gauge with gas and then sealing the container so that no gas may escape. If the container is cooled, the gas inside likewise gets colder and its pressure is observed to decrease. Since the container is rigid and tightly sealed, both the volume and number of moles of gas remain constant. If we heat the container, the gas inside gets hotter (Figure 8) and the pressure increases.

This figure includes three similar diagrams. In the first diagram to the left, a rigid spherical container of a gas to which a pressure gauge is attached at the top is placed in a large beaker of water, indicated in light blue, atop a hot plate. The needle on the pressure gauge points to the far left on the gauge. The diagram is labeled “low P” above and “hot plate off” below. The second similar diagram also has the rigid spherical container of gas placed in a large beaker from which light blue wavy line segments extend from the top of the liquid in the beaker. The beaker is situated on top of a slightly reddened circular area. The needle on the pressure gauge points straight up, or to the middle on the gauge. The diagram is labeled “medium P” above and “hot plate on medium” below. The third diagram also has the rigid spherical container of gas placed in a large beaker in which bubbles appear near the liquid surface and several wavy light blue line segments extend from the surface out of the beaker. The beaker is situated on top of a bright red circular area. The needle on the pressure gauge points to the far right on the gauge. The diagram is labeled “high P” above and “hot plate on high” below.
Figure 8. The effect of temperature on gas pressure. When the hot plate is off, the pressure of the gas in the container is relatively low. As the gas is heated, the pressure of the gas in the container increases.

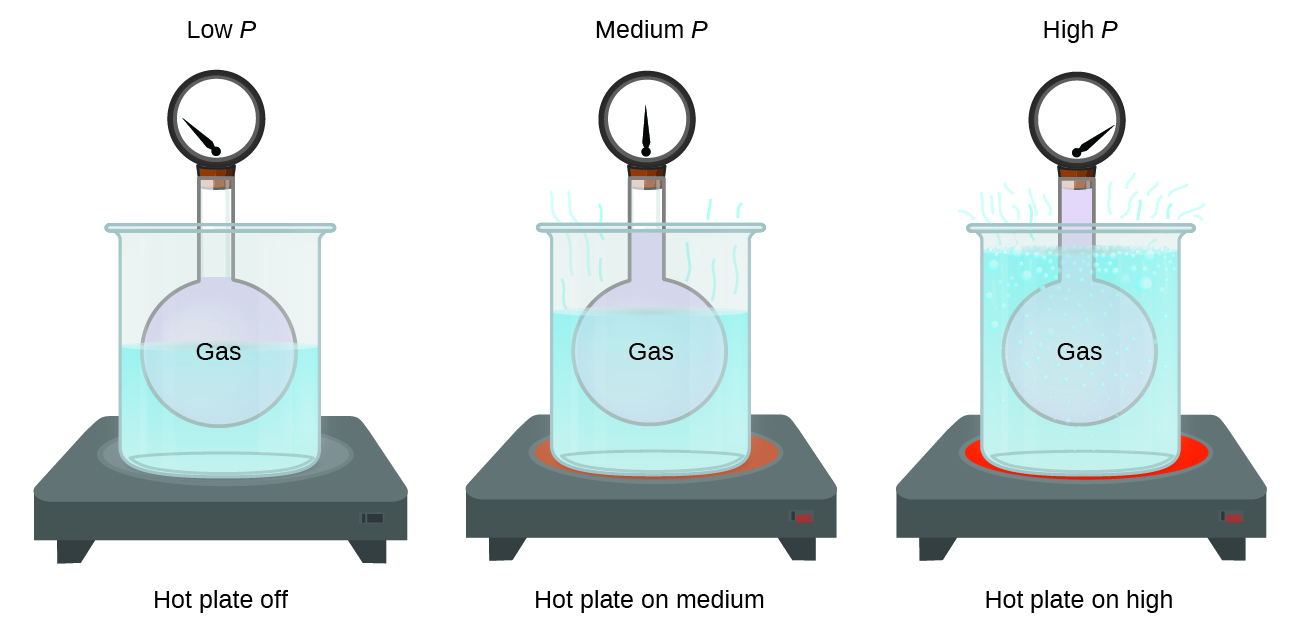
This direct relationship between temperature and pressure is observed for any sample of gas confined to a constant volume. An example of experimental pressure-temperature data is shown for a sample of air under these conditions in Figure 9. We find that temperature and pressure are linearly related, and if the temperature is on the kelvin scale, then P and T are directly proportional (again, when volume and moles of gas are held constant); if the temperature on the kelvin scale increases by a certain factor, the gas pressure increases by the same factor.

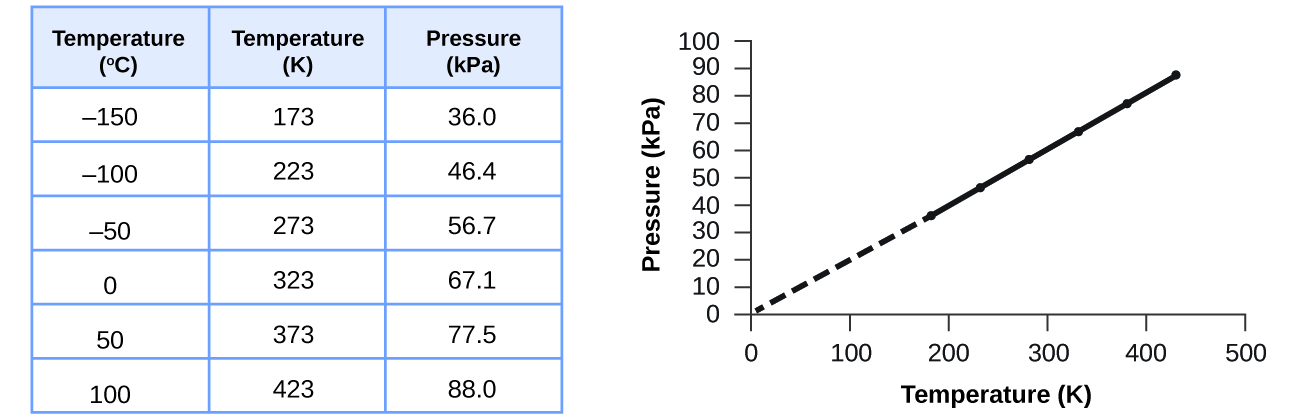
This figure includes a table and a graph. The table has 3 columns and 7 rows. The first row is a header, which labels the columns “Temperature, degrees C,” “Temperature, K,” and “Pressure, k P a.” The first column contains the values from top to bottom negative 150, negative 100, negative 50, 0, 50, and 100. The second column contains the values from top to bottom 173, 223, 273, 323, 373, and 423. The third column contains the values 36.0, 46.4, 56.7, 67.1, 77.5, and 88.0. A graph appears to the right of the table. The horizontal axis is labeled “Temperature ( K ).” with markings and labels provided for multiples of 100 beginning at 0 and ending at 500. The vertical axis is labeled “Pressure ( k P a )” with markings and labels provided for multiples of 10, beginning at 0 and ending at 100. Six data points from the table are plotted on the graph with black dots. These dots are connected with a solid black line. A dashed line extends from the data point furthest to the left to the origin. The graph shows a positive linear trend.
Figure 9. For a constant volume and amount of air, the pressure and temperature are directly proportional, provided the temperature is in kelvin. (Measurements cannot be made at lower temperatures because of the condensation of the gas.) When this line is extrapolated to lower pressures, it reaches a pressure of 0 kPa at –273 °C, which is 0 on the kelvin scale and the lowest possible temperature, called absolute zero.

Guillaume Amontons was the first to empirically establish the relationship between the pressure and the temperature of a gas (in ~1700), and Joseph Louis Gay-Lussac determined the relationship more precisely (in ~1800). Because of this, the P–T relationship for gases is known as either Amontons’s law or Gay-Lussac’s law. Under either name, it states that the pressure of a given amount of gas is directly proportional to its temperature on the kelvin scale when the volume is held constant. Mathematically, this can be written:

 P   ∝  T       or          P   =  constant · T           or        P   =   k · T        or       [latex]\frac{\text{P}_{1}}{\text{T}_{1}}[/latex]  =  [latex]\frac{\text{P}_{2}}{\text{T}_{2}}[/latex]

where ∝ means “is proportional to,” and k is a proportionality constant that depends on the identity, amount, and volume of the gas.

For a confined, constant volume of gas, the ratio [latex]\frac{\text{P}}{\text{T}}[/latex] is therefore constant (i.e., [latex]\frac{\text{P}}{\text{T}}[/latex]  =  k). If the gas is initially in “Condition 1” (with P  =  P1 and T  =  T1), and then changes to “Condition 2” (with P  =  P2 and T  =  T2), we have that [latex]\frac{\text{P}_{1}}{\text{T}_{1}}[/latex]  =  k and [latex]\frac{\text{P}_{2}}{\text{T}_{2}}[/latex]  =  k, which reduces to [latex]\frac{\text{P}_{1}}{\text{T}_{1}}[/latex]  =  [latex]\frac{\text{P}_{2}}{\text{T}_{2}}[/latex]. This equation is useful for pressure-temperature calculations for a confined gas at constant volume. Note that temperatures must be on the kelvin scale for any gas law calculations (0 on the kelvin scale, the lowest possible temperature, is called absolute zero). Also note that there are at least three ways we can describe how the pressure of a gas changes as its temperature changes. We can use a table of values, a graph, or a mathematical equation.

Example 2

Predicting Change in Pressure with Temperature
A can of hair spray is used until it is empty except for the propellant, isobutane gas.

(a) On the can is the warning “Store only at temperatures below 120 °F (48.8 °C). Do not incinerate.” Why?

(b) The gas in the can is initially at 24 °C and 360 kPa, and the can has a volume of 350 mL. If the can is left in a car that reaches 50 °C on a hot day, what is the new pressure in the can?

Solution
(a) The can contains an amount of isobutane gas at a constant volume, so if the temperature is increased by heating, the pressure will increase proportionately. High temperature could lead to high pressure, causing the can to burst. (Also, isobutane is combustible, so incineration could cause the can to explode.)

(b) We are looking for a pressure change due to a temperature change at constant volume, so we will use Amontons’s/Gay-Lussac’s law. Taking P1 and T1 as the initial values, T2 as the temperature where the pressure is unknown and P2 as the unknown pressure, and converting °C to K, we have:

[latex]\frac{\text{P}_{1}}{\text{T}_{1}}[/latex]  =  [latex]\frac{\text{P}_{2}}{\text{T}_{2}}[/latex]  which means that  [latex]\frac{360\;\text{kPa}}{297\;\text{K}}[/latex]  =  [latex]\frac{\text{P}_{2}}{323\;\text{K}}[/latex]

Rearranging and solving gives: P2  =   [latex]\frac{360\;\text{kPa}\;\times\; 323 \;\rule[0.25ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{K}}{297 \;\rule[0.25ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{K}}[/latex]  =  391.5 kPa

Check Your Learning
A sample of nitrogen, N2, occupies 45.0 mL at 27 °C and 600 torr. What pressure will it have if cooled to –73 °C while the volume remains constant?

Answer:

400 torr

Volume and Temperature Relationship for Ideal Gases

If we fill a balloon with air and seal it, the balloon contains a specific amount of air at atmospheric pressure, about 1 atm. If we put the balloon in a refrigerator, the gas inside gets cold and the balloon shrinks (although both the amount of gas and its pressure remain constant). If we make the balloon very cold, it will shrink a great deal, and it expands again when it warms up.

Demonstration: Charles’s law

Set up. In the following demonstration, a balloon is filled with air and sealed. The balloon contains a specific amount of air at atmospheric pressure. Then liquid nitrogen is poured onto the balloon to cool the balloon. The pressure and number of moles of gas are constant in this experiment.

Explanation. As the air inside the balloon is cooled, the volume of the balloon decreases. This illustrates that as temperature of a gas decreases, the volume occupied by that gas also decreases, causing the balloon to shrink. When liquid nitrogen is not poured onto the balloon and the balloon is allowed to warm up again, the balloon re-expands to its original volume.

These examples of the effect of temperature on the volume of a given amount of a confined gas at constant pressure are true in general: The volume increases as the temperature increases, and decreases as the temperature decreases. Volume-temperature data for a 1 mole sample of methane gas at 1 atm are listed and graphed in Figure 10.

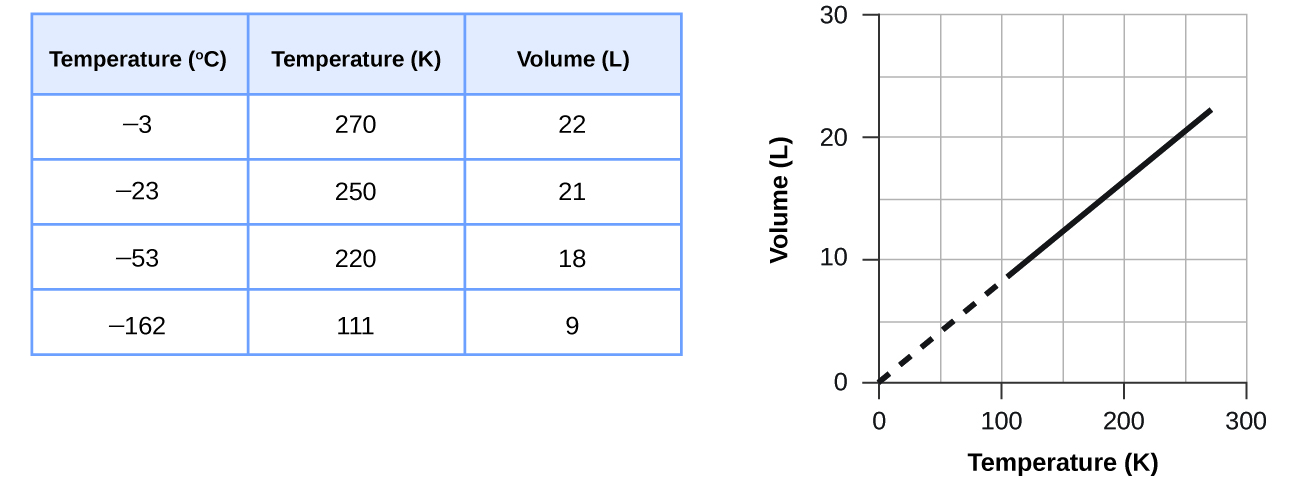
This figure includes a table and a graph. The table has 3 columns and 6 rows. The first row is a header, which labels the columns “Temperature, degrees C,” “Temperature, K,” and “Pressure, k P a.” The first column contains the values from top to bottom negative 100, negative 50, 0, 100, and 200. The second column contains the values from top to bottom 173, 223, 273, 373, and 473. The third column contains the values 14.10, 18.26, 22.40, 30.65, and 38.88. A graph appears to the right of the table. The horizontal axis is labeled “Temperature ( K ).” with markings and labels provided for multiples of 100 beginning at 0 and ending at 300. The vertical axis is labeled “Volume ( L )” with marking and labels provided for multiples of 10, beginning at 0 and ending at 30. Five data points from the table are plotted on the graph with black dots. These dots are connected with a solid black line. The graph shows a positive linear trend.
Figure 10. The volume and temperature are linearly related for 1 mole of methane gas at a constant pressure of 1 atm. If the temperature is in kelvin, volume and temperature are directly proportional. The line stops at 111 K because methane liquefies at this temperature; when extrapolated, it intersects the graph’s origin, representing a temperature of absolute zero.

The relationship between the volume and temperature of a given amount of gas at constant pressure is known as Charles’s law in recognition of the French scientist and balloon flight pioneer Jacques Alexandre César Charles. Charles’s law states that the volume of a given amount of gas is directly proportional to its temperature on the kelvin scale when the pressure is held constant.

Mathematically, this can be written as:

 V  ∝  T     or     V  =  constant · T     or      V  =  k · T      or      [latex]\frac{\text{V}_{1}}{\text{T}_{1}}[/latex]  =  [latex]\frac{\text{V}_{2}}{\text{T}_{2}}[/latex]

with k being a proportionality constant that depends on the amount and pressure of the gas.

For a confined, constant pressure gas sample, [latex]\frac{\text{V}}{\text{T}}[/latex] is constant (i.e., the ratio  =  k), and as seen with the P–T relationship, this leads to another form of Charles’s law: [latex]\frac{\text{V}_{1}}{\text{T}_{1}}[/latex]  =  [latex]\frac{\text{V}_{2}}{\text{T}_{2}}[/latex]

Example 3

Predicting Change in Volume with Temperature
A sample of carbon dioxide, CO2, occupies 0.300 L at 10 °C and 750 torr. What volume will the gas have at 30 °C and 750 torr?

Solution
Because we are looking for the volume change caused by a temperature change at constant pressure, this is a job for Charles’s law. Taking V1 and T1 as the initial values, T2 as the temperature at which the volume is unknown and V2 as the unknown volume, and converting °C into K we have:

[latex]\frac{\text{V}_{1}}{\text{T}_{1}}[/latex]  =  [latex]\frac{\text{V}_{2}}{\text{T}_{2}}[/latex]  which means that  [latex]\frac{0.300\;\text{L}}{283 \;\text{K}}[/latex]  =  [latex]\frac{\text{V}_{2}}{303\;\text{K}}[/latex]
Rearranging and solving gives:
V2  =  [latex]\frac{0.300\;\text{L}\;\times\; 303 \;\rule[0.25ex]{0.8em}{0.1ex}\hspace{-0.8em}\text{K} }{283 \;\rule[0.25ex]{0.8em}{0.1ex}\hspace{-0.8em}\text{K}}[/latex]  =  0.321 L

This answer supports our expectation from Charles’s law, namely, that raising the gas temperature (from 283 K to 303 K) at a constant pressure will yield an increase in its volume (from 0.300 L to 0.321 L).

Check Your Learning
A sample of oxygen, O2, occupies 32.2 mL at 30 °C and 452 torr. What volume will it occupy at –70 °C and the same pressure?

Answer:

21.6 mL

Example 4

Measuring Temperature with a Volume Change
Temperature is sometimes measured with a gas thermometer by observing the change in the volume of the gas as the temperature changes at constant pressure. The hydrogen in a particular hydrogen gas thermometer has a volume of 150.0 cm3 when immersed in a mixture of ice and water (0.00 °C). When immersed in boiling liquid ammonia, the volume of the hydrogen, at the same pressure, is 131.7 cm3. Find the temperature of boiling ammonia on the kelvin and Celsius scales.

Solution
A volume change caused by a temperature change at constant pressure means we should use Charles’s law. Taking V1 and T1 as the initial values, T2 as the temperature at which the volume is unknown and V2 as the unknown volume, and converting °C into K we have:

[latex]\frac{\text{V}_{1}}{\text{T}_{1}}[/latex]  =  [latex]\frac{\text{V}_{2}}{\text{T}_{2}}[/latex]  which means that  [latex]\frac{150.0 \;\text{cm}^3}{273.15 \;\text{K}}[/latex]  =  [latex]\frac{131.7 \;\text{cm}^3}{\text{T}_{2}}[/latex]

Rearrangement gives:

T2  =  [latex]\frac{131.7 \;\rule[0.25ex]{0.8em}{0.1ex}\hspace{-0.8em}\text{cm}^3 \times 273.15 \;\text{K} }{150.0 \;\rule[0.25ex]{0.8em}{0.1ex}\hspace{-0.8em}\text{cm}^3}[/latex]  =  239.8 K

Subtracting 273.15 from 239.8 K, we find that the temperature of the boiling ammonia on the Celsius scale is –33.4 °C.

Check Your Learning
What is the volume of a sample of ethane at 467 K and 1.1 atm if it occupies 405 mL at 298 K and 1.1 atm?

Answer:

635 mL

Volume and Pressure Relationship for Ideal Gases

If we fill an airtight syringe with air, the syringe contains a specific amount of air at constant temperature, say 25 °C. If we slowly push in the plunger while keeping temperature constant, the gas in the syringe is compressed into a smaller volume and its pressure increases; if we pull out the plunger, the volume increases and the pressure decreases. This example of the effect of volume on the pressure of a given amount of a confined gas is true in general. Decreasing the volume of a contained gas will increase its pressure, and increasing its volume will decrease its pressure. In fact, if the volume increases by a certain factor, the pressure decreases by the same factor, and vice versa. Volume-pressure data for an air sample at room temperature are graphed in Figure 11.

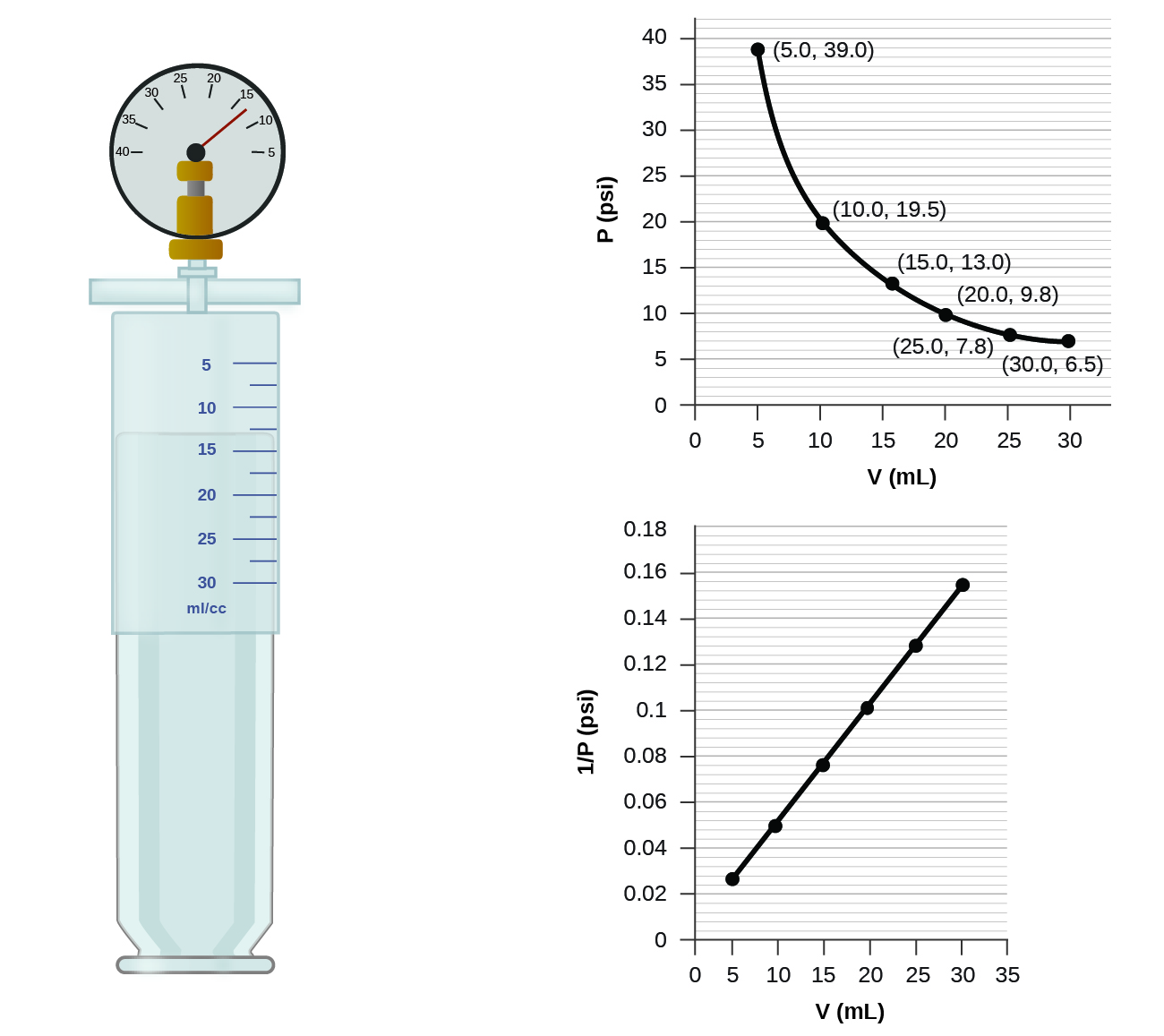
This figure contains a diagram and two graphs. The diagram shows a syringe labeled with a scale in m l or c c with multiples of 5 labeled beginning at 5 and ending at 30. The markings halfway between these measurements are also provided. Attached at the top of the syringe is a pressure gauge with a scale marked by fives from 40 on the left to 5 on the right. The gauge needle rests between 10 and 15, slightly closer to 15. The syringe plunger position indicates a volume measurement about halfway between 10 and 15 m l or c c. The first graph is labeled “V ( m L )” on the horizontal axis and “P ( p s i )” on the vertical axis. Points are labeled at 5, 10, 15, 20, and 25 m L with corresponding values of 39.0, 19.5, 13.0, 9.8, and 6.5 p s i. The points are connected with a smooth curve that is declining at a decreasing rate of change. The second graph is labeled “V ( m L )” on the horizontal axis and “1 divided by P ( p s i )” on the vertical axis. The horizontal axis is labeled at multiples of 5, beginning at zero and extending up to 35 m L. The vertical axis is labeled by multiples of 0.02, beginning at 0 and extending up to 0.18. Six points indicated by black dots on this graph are connected with a black line segment showing a positive linear trend.
Figure 11. When a gas occupies a smaller volume, it exerts a higher pressure; when it occupies a larger volume, it exerts a lower pressure (assuming the amount of gas and the temperature do not change). Since P and V are inversely proportional, a graph of 1/P vs. V is linear.

Unlike the P–T and V–T relationships, pressure and volume are not directly proportional to each other. Instead, P and V exhibit inverse proportionality: Increasing the pressure results in a decrease of the volume of the gas. Mathematically this can be written:

 P  ∝  1/V          or      P  =  k · 1/V       or        P · V  =  k         or          P1 V1  =  P2 V2

with k being a constant. Graphically, this relationship is shown by the straight line that results when plotting the inverse of the pressure ([latex]\frac{1}{\text{P}}[/latex]) versus the volume (V), or the inverse of volume ([latex]\frac{1}{\text{V}}[/latex]) versus the pressure (P).

The relationship between the volume and pressure of a given amount of gas at constant temperature was first published by the English natural philosopher Robert Boyle over 300 years ago. It is summarized in the statement now known as Boyle’s law: The volume of a given amount of gas held at constant temperature is inversely proportional to the pressure under which it is measured.

Demonstration: Boyle’s Law

Set up. In the following demonstration, a small amount of shaving cream is sprayed into a bell jar. A vacuum pump is then used to remove air molecules from the bell jar and the pressure inside the bell jar around the shaving cream decreases. The vacuum is then turned off, and the bell jar is sealed by closing a valve. The tube that connects the bell jar to the vacuum pump is removed. At the end of the video, the valve is opened to allow air to flow back into the bell jar. In this scenario, the temperature of the gas within the shaving cream and the number of molecules of gas within the shaving cream are kept constant.

Explanation. Shaving cream is a foam in which air is trapped in tiny soap bubbles. As the pressure around the shaving cream decreases, the volume occupied by the gas inside the bubbles increases, causing the shaving cream foam to expand. When the vacuum is released and the pressure surrounding the shaving cream is rapidly increased, the shaving cream collapses as the volume decreases.

Example 5

Volume of a Gas Sample
The sample of gas in Figure 11 has a volume of 15.0 mL at a pressure of 13.0 psi. Determine the pressure of the gas at a volume of 7.5 mL, using:

(a) the P–V graph in Figure 11

(b) the [latex]\frac{1}{P}[/latex] vs. V graph in Figure 11

(c) the Boyle’s law equation

Comment on the likely accuracy of each method.

Solution
(a) Estimating from the P–V graph gives a value for P somewhere around 27 psi.

(b) Estimating from the [latex]\frac{1}{P}[/latex] versus V graph give a value of about 26 psi.

(c) From Boyle’s law, we know that the product of pressure and volume (PV) for a given sample of gas at a constant temperature is always equal to the same value. Therefore we have P1V1  =  k and P2V2  =  k which means that P1V1  =  P2V2.

Using P1 and V1 as the known values 13.0 psi and 15.0 mL, P2 as the pressure at which the volume is unknown, and V2 as the unknown volume, we have:

P1V1  =  P2V2  or  13.0 psi  ×  15.0 mL  =  P2  ×  7.5 mL
Solving:
P2  =  [latex]\frac{13.0 \;\text{psi}\;\times\; 15.0 \;\rule[0.5ex]{1.2em}{0.1ex}\hspace{-1.2em}\text{mL}}{7.5 \;\rule[0.5ex]{1.2em}{0.1ex}\hspace{-1.2em}\text{mL}}[/latex]  =  26 psi

It was more difficult to estimate well from the P–V graph, so (a) is likely more inaccurate than (b) or (c). The calculation will be as accurate as the equation and measurements allow.

Check Your Learning
The sample of gas in Figure 11 has a volume of 30.0 mL at a pressure of 6.5 psi. Determine the volume of the gas at a pressure of 11.0 psi, using:

(a) the P–V graph in Figure 11

(b) the [latex]\frac{1}{P}[/latex] vs. V graph in Figure 11

(c) the Boyle’s law equation

Comment on the likely accuracy of each method.

Answer:

(a) about 17–18 mL; (b) ~18 mL; (c) 17.7 mL; it was more difficult to estimate well from the P–V graph, so (a) is likely more inaccurate than (b); the calculation will be as accurate as the equation and measurements allow.

Moles of Gas and Volume Relationship for Ideal Gases

The Italian scientist Amedeo Avogadro advanced a hypothesis in 1811 to account for the behavior of gases, stating that equal volumes of all gases, measured under the same conditions of temperature and pressure, contain the same number of molecules. Over time, this relationship was supported by many experimental observations as expressed by Avogadro’s law: For a confined gas, the volume (V) and number of moles (n) are directly proportional if the pressure and temperature both remain constant.

In equation form, this is written as:

V  ∝  n        or        V  =  k · n       or         [latex]\frac{\text{V}_{1}}{n_{1}}[/latex]  =  [latex]\frac{\text{V}_{2}}{n_{2}}[/latex]

Mathematical relationships can also be determined for the other variable pairs, such as P versus n, and n versus T.

Visit this interactive PhET simulation to investigate the relationships between pressure, volume, temperature, and amount of gas. Use the simulation to examine the effect of changing one parameter on another while holding the other parameters constant (as described in the preceding sections on the various gas laws).

The Ideal Gas Law

To this point, four separate laws have been discussed that relate pressure, volume, temperature, and the number of moles of the gas:

  • PV  =  constant (with T and n held constant)
  • P/T  =  constant (with V and n held constant)
  • V/T  =  constant (with P and n held constant)
  • V/n  =  constant (with P and T held constant)

Combining these four laws yields the ideal gas law, a relation between the pressure, volume, temperature, and number of moles of a gas:

 PV  =  nRT

where P is the pressure of a gas, V is its volume, n is the number of moles of the gas, T is its temperature on the kelvin scale, and R is a constant called the ideal gas constant or the universal gas constant. The units used to express pressure, volume, and temperature will determine the proper form of the gas constant as required by dimensional analysis, the most commonly encountered values being 0.08206 L atm mol–1 K–1 and 8.314 J mol–1 K–1.

An ideal gas consists of particles (atoms or molecules) that have the following properties:

  1. Particles have no volume.
    They are very small compared to the size of the container and compared to the distance between them.
  2. Particles exert no forces on each other.
    Particles are neither attracted to, nor repelled from, each other.
  3. Particles are in constant motion.
    They undergo billiard-ball-like collisions with the walls of the container and with each other.

All the calculations presented in this module assume ideal gas behavior. However, this assumption is only reasonable for gases at relatively low pressure and high temperature. In future courses you might explore a modified gas law that accounts for the non-ideal behavior observed for many gases at relatively high pressures and low temperatures.

The ideal gas equation contains four variables, P, V, n, and T, and the gas constant R. Typically any three of these variables will permit use of the ideal gas law to calculate the fourth variable as demonstrated in the following example exercises.

Example 6

Using the Ideal Gas Law
Methane, CH4, is being considered for use as an alternative automotive fuel to replace gasoline. One gallon of gasoline could be replaced by 655 g of CH4. What is the volume of this much methane at 25 °C and 745 torr?

Solution
We must rearrange PV  =  nRT to solve for V:

V  =  [latex]\frac{\text{nRT}}{\text{P}}[/latex]

If we choose to use R = 0.08206 L atm mol–1 K–1, then the amount must be in moles, temperature must be in kelvin, and pressure must be in atm.

Converting into the “right” units:

n  =  655 g CH4 × [latex]\frac{1 \;\text{mol}}{16.043 \;\rule[0.5ex]{2.2em}{0.1ex}\hspace{-2.2em}\text{g CH}_4}[/latex]  =  40.8 mol
T  =  25 °C + 273  =  298 K
P  =  745 torr  × [latex]\frac{1 \;\text{atm}}{760 \;\rule[0.5ex]{1.4em}{0.1ex}\hspace{-1.4em}\text{torr}}[/latex]  =  0.980 atm
V  =  [latex]\frac{\text{nRT}}{\text{P}}[/latex]  =  [latex]\frac{(40.8 \;\rule[0.5ex]{1.2em}{0.1ex}\hspace{-1.2em}\text{mol})(0.08206 \text{L}\;\rule[0.5ex]{5.1em}{0.1ex}\hspace{-5.1em}\text{atm mol}^{-1} \;\text{K}^{-1})(298 \;\rule[0.5ex]{0.6em}{0.1ex}\hspace{-0.6em}\text{K})}{0.980 \;\rule[0.5ex]{1.5em}{0.1ex}\hspace{-1.5em}\text{atm}}[/latex]  =  1.02 × 103 L
It would require 1020 L (269 gal) of gaseous methane at about 1 atm of pressure to replace 1 gal of gasoline. It requires a large container to hold enough methane at 1 atm to replace several gallons of gasoline.

Check Your Learning
Calculate the pressure in bar of 2520 moles of hydrogen gas stored at 27 °C in the 180-L storage tank of a modern hydrogen-powered car.

Answer:

350 bar

If the number of moles of an ideal gas are kept constant under two different sets of conditions, a useful mathematical relationship called the combined gas law is obtained: [latex]\frac{\text{P}_{1}\text{V}_{1}}{\text{T}_{1}}[/latex]  =  [latex]\frac{\text{P}_{2}\text{V}_{2}}{\text{T}_{2}}[/latex] using units of atm, L, and K. Both sets of conditions are equal to the product of n × R (where n  =  the number of moles of the gas and R is the ideal gas law constant).

Example 7

Using the Combined Gas Law
When filled with air, a typical scuba tank with a volume of 13.2 L has a pressure of 153 atm (Figure 13). If the water temperature is 27 °C, how many liters of air will such a tank provide to a diver’s lungs at a depth of approximately 70 feet in the ocean where the pressure is 3.13 atm?

This photograph shows a scuba diver underwater with a tank on his or her back and bubbles ascending from the breathing apparatus.
Figure 13. Scuba divers use compressed air to breathe while underwater. (credit: modification of work by Mark Goodchild)

Letting 1 represent the air in the scuba tank and 2 represent the air in the lungs, and noting that body temperature (the temperature the air will be in the lungs) is 37 °C, we have:

[latex]\frac{\text{P}_{1}\text{V}_{1}}{\text{T}_{1}}[/latex]  =  [latex]\frac{\text{P}_{2}\text{V}_{2}}{\text{T}_{2}}[/latex]  →  [latex]\frac{(153 \;\text{atm})(13.2 \;\text{L})}{(300 \;\text{K})}[/latex]  =  [latex]\frac{(3.13 \;\text{atm})(V_2)}{(310 \;\text{K})}[/latex]

Solving for V2:

V2  =  [latex]\frac{(153 \;\rule[0.5ex]{1.2em}{0.1ex}\hspace{-1.2em}\text{atm})(13.2 \;\text{L})(310 \;\rule[0.5ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{K})}{(300 \;\rule[0.5ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{K})(3.13 \;\rule[0.5ex]{1.2em}{0.1ex}\hspace{-1.2em}\text{atm})}[/latex]  =  667 L

(Note: Be advised that this particular example is one in which the assumption of ideal gas behavior is not very reasonable, since it involves gases at relatively high pressures and low temperatures. Despite this limitation, the calculated volume can be viewed as a good “ballpark” estimate.)

Check Your Learning
A sample of ammonia is found to occupy 0.250 L under laboratory conditions of 27 °C and 0.850 atm. Find the volume of this sample at 0 °C and 1.00 atm.

Answer:

0.193 L

Chemistry in Real Life: The Interdependence between Ocean Depth and Pressure in Scuba Diving

Whether scuba diving at the Great Barrier Reef in Australia (shown in Figure 14) or in the Caribbean, divers must understand how pressure affects a number of issues related to their comfort and safety.

This picture shows colorful underwater corals and anemones in hues of yellow, orange, green, and brown, surrounded by water that appears blue in color.
Figure 14. Scuba divers, whether at the Great Barrier Reef or in the Caribbean, must be aware of buoyancy, pressure equalization, and the amount of time they spend underwater, to avoid the risks associated with pressurized gases in the body. (credit: Kyle Taylor)

The pressure a diver experiences is the sum of all pressures above the diver (from the water and the air) and therefore increases with depth. Most pressure measurements are given in units of atmospheres, expressed as “atmospheres absolute” or ATA in the diving community: Every 33 feet of salt water represents 1 ATA of pressure in addition to 1 ATA of pressure from the atmosphere at sea level. As a diver descends, the increase in pressure causes the body’s air pockets in the ears and lungs to compress; on the ascent, the decrease in pressure causes these air pockets to expand, potentially rupturing eardrums or bursting the lungs. Divers must therefore undergo equalization by adding air to body airspaces on the descent by breathing normally and adding air to the mask by breathing out of the nose or adding air to the ears and sinuses by equalization techniques; the corollary is also true on ascent, divers must release air from the body to maintain equalization. Buoyancy, or the ability to control whether a diver sinks or floats, is controlled by the buoyancy compensator (BCD). If a diver is ascending, the air in his BCD expands because of lower pressure according to Boyle’s law (decreasing the pressure of gases increases the volume). The expanding air increases the buoyancy of the diver, and she or he begins to ascend. The diver must vent air from the BCD or risk an uncontrolled ascent that could rupture the lungs. In descending, the increased pressure causes the air in the BCD to compress and the diver sinks much more quickly; the diver must add air to the BCD or risk an uncontrolled descent, facing much higher pressures near the ocean floor. The pressure also impacts how long a diver can stay underwater before ascending. The deeper a diver dives, the more compressed the air that is breathed because of increased pressure: If a diver dives 33 feet, the pressure is 2 ATA and the air would be compressed to one-half of its original volume. The diver uses up available air twice as fast as at the surface.

Standard Conditions of Temperature and Pressure

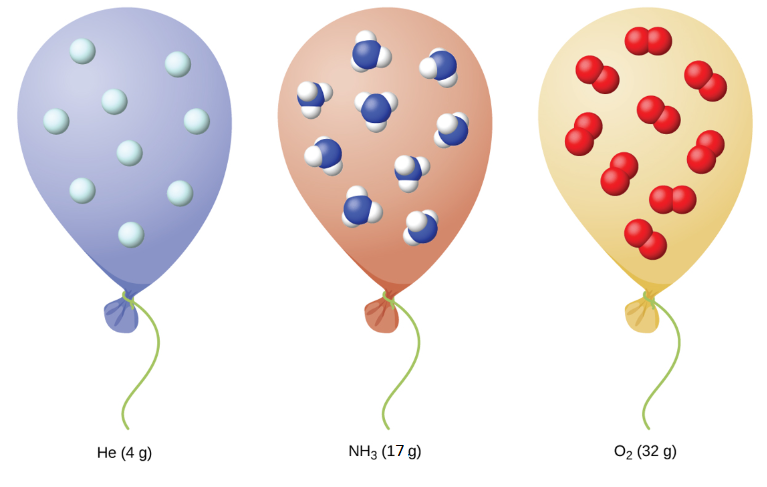
We have seen that the volume of a given quantity of gas and the number of molecules (moles) in a given volume of gas vary with changes in pressure and temperature. Chemists sometimes make comparisons against a standard temperature and pressure (STP) for reporting properties of gases: 273.15 K and 1 atm (101.325 kPa). At STP, an ideal gas has a volume of about 22.4 L—this is referred to as the standard molar volume (Figure 15).

Key Concepts and Summary

Gases exert pressure, which is force per unit area. The pressure of a gas may be expressed in the SI unit of pascal or kilopascal, as well as in many other units including torr, atmosphere, and bar. Atmospheric pressure is measured using a barometer; other gas pressures can be measured using one of several types of manometers.

The behavior of gases can be described by several laws based on experimental observations of their properties. The pressure of a given amount of gas is directly proportional to its absolute temperature, provided that the volume does not change (Amontons’s law). The volume of a given gas sample is directly proportional to its absolute temperature at constant pressure (Charles’s law). The volume of a given amount of gas is inversely proportional to its pressure when temperature is held constant (Boyle’s law). Under the same conditions of temperature and pressure, equal volumes of all gases contain the same number of molecules (Avogadro’s law).

The equations describing these laws are special cases of the ideal gas law, PV  =  nRT, where P is the pressure of the gas, V is its volume, n is the number of moles of the gas, T is its kelvin temperature, and R is the ideal (universal) gas constant.

Key Equations

  • P  =  [latex]\frac{\text{F}}{\text{A}}[/latex]
  • PV  =  nRT
    where R  =  0.08206 L atm mol–1 K–1

Glossary

absolute zero
temperature at which the volume of a gas would be zero according to Charles’s law.
Amontons’s law
(also, Gay-Lussac’s law) pressure of a given number of moles of gas is directly proportional to its kelvin temperature when the volume is held constant

atmosphere (atm)
unit of pressure; 1 atm  =  101,325 Pa

Avogadro’s law
volume of a gas at constant temperature and pressure is proportional to the number of gas molecules

bar
(bar or b) unit of pressure; 1 bar  =  100,000 Pa

barometer
device used to measure atmospheric pressure
Boyle’s law
volume of a given number of moles of gas held at constant temperature is inversely proportional to the pressure under which it is measured
Charles’s law
volume of a given number of moles of gas is directly proportional to its kelvin temperature when the pressure is held constant

hydrostatic pressure
pressure exerted by a fluid due to gravity

ideal gas
hypothetical gas whose physical properties are perfectly described by the gas laws
ideal gas constant (R)
constant derived from the ideal gas equation R  =  0.08206 L atm mol–1 K–1 or 8.314 L kPa mol–1 K–1
ideal gas law
relation between the pressure, volume, amount, and temperature of a gas under conditions derived by combination of the simple gas laws
pascal (Pa)
SI unit of pressure; 1 Pa  =  1 N/m2
pounds per square inch (psi)
unit of pressure common in the US
pressure
force exerted per unit area
standard conditions of temperature and pressure (STP)
273.15 K (0 °C) and 1 atm (101.325 kPa)
standard molar volume
volume of 1 mole of gas at STP, approximately 22.4 L for gases behaving ideally
torr
unit of pressure; [latex]1 \;\text{torr} = \frac{1}{760} \;\text{atm}[/latex]

Chemistry End of Section Exercises

Pressure

  1. Why are sharp knives more effective than dull knives (Hint: think about the definition of pressure)?
  2. Why do some small bridges have weight limits that depend on how many wheels or axles the crossing vehicle has?
  3. Why should you roll or belly-crawl rather than walk across a thinly-frozen pond?
  4. A typical barometric pressure in Kansas City is 740 torr. What is this pressure in atmospheres, in millimeters of mercury, and in kilopascals?
  5. Canadian tire pressure gauges are marked in units of kilopascals. What reading on such a gauge corresponds to 32 psi?
  6. During the Viking landings on Mars, the atmospheric pressure was determined to be on the average about 6.50 millibars (1 bar = 0.987 atm). What is that pressure in torr and kPa?
  7. The pressure of the atmosphere on the surface of the planet Venus is about 88.8 atm. Compare that pressure in psi to the normal pressure on earth at sea level in psi.
  8. A medical laboratory catalog describes the pressure in a cylinder of a gas as 14.82 MPa. What is the pressure of this gas in atmospheres and torr?
  9. Consider this scenario and answer the following questions: On a mid-August day in the northeastern United States, the following information appeared in the local newspaper: atmospheric pressure at sea level 29.97 in., 1013.9 mbar.
    1. What was the pressure in kPa?
    2. The pressure near the seacoast in the northeastern United States is usually reported near 30.0 in. Hg. During a hurricane, the pressure may fall to near 28.0 in. Hg. Calculate the drop in pressure in torr.
  10. Why is it necessary to use a nonvolatile liquid in a barometer?

Gas Laws

  1. Sometimes leaving a bicycle in the sun on a hot day will cause a blowout. Why?
  2. Explain how the volume of the bubbles exhausted by a scuba diver change as they rise to the surface, assuming that they remain intact.
  3. One way to state Boyle’s law is “All other things being equal, the pressure of a gas is inversely proportional to its volume.”
    1. What is the meaning of the term “inversely proportional?”
    2. What are the “other things” that must be equal?
  4. An alternate way to state Avogadro’s law is “All other things being equal, the number of molecules in a gas is directly proportional to the volume of the gas.”
    1. What is the meaning of the term “directly proportional?”
    2. What are the “other things” that must be equal?
  5. How would the graph in Figure 11 change if the number of moles of gas in the sample used to determine the curve were doubled?
  6. Determine the volume of 1 mol of CH4 gas at 150 K and 1 atm, using Figure 10.
  7. Determine the pressure of the gas in the syringe shown in Figure 11 when its volume is 12.5 mL, using:
    1. the appropriate graph
    2. Boyle’s law
  8. A spray can is used until it is empty except for the propellant gas, which has a pressure of 1344 torr at 23 °C. If the can is thrown into a fire (T  =  475 °C), what will be the pressure in the hot can?
  9. What is the temperature of an 11.2-L sample of carbon monoxide, CO, at 744 torr if it occupies 13.3 L at 55 °C and 744 torr?
  10. A 2.50-L volume of hydrogen measured at –196 °C is warmed to 100 °C. Calculate the volume of the gas at the higher temperature, assuming no change in pressure.
  11. A weather balloon contains 8.80 moles of helium at a pressure of 0.992 atm and a temperature of 25 °C at ground level. What is the volume of the balloon under these conditions?
    This image shows a white balloon that appears to have an attached white card. The balloon is being held by a person in an outdoor setting.
  12. The volume of an automobile air bag was 66.8 L when inflated at 25 °C with 77.8 g of nitrogen gas. What was the pressure in the bag in kPa?
  13. Iodine, I2, is a solid at room temperature but sublimes (converts from a solid into a gas) when warmed. What is the temperature in a 73.3-mL bulb that contains 0.292 g of I2 vapor at a pressure of 0.462 atm?
  14. How many grams of gas are present in each of the following cases?
    1. 0.100 L of CO2 at 307 torr and 26 °C
    2. 8.75 L of C2H4, at 378.3 kPa and 483 K
    3. 221 mL of Ar at 0.23 torr and –54 °C
  15. A cylinder of medical oxygen has a volume of 35.4 L, and contains O2 at a pressure of 151 atm and a temperature of 25 °C. What volume of O2 does this correspond to at normal body conditions, that is, 1 atm and 37 °C?
  16. A large scuba tank (Figure 13) with a volume of 18 L is rated for a pressure of 220 bar. The tank is filled at 20 °C and contains enough air to supply 1860 L of air to a diver at a pressure of 2.37 atm (a depth of 45 feet). Was the tank filled to capacity at 20 °C?
  17. While resting, the average 70-kg human male consumes 14 L of pure O2 per hour at 25 °C and 100 kPa. How many moles of O2 are consumed by a 70 kg man while resting for 1.0 h?
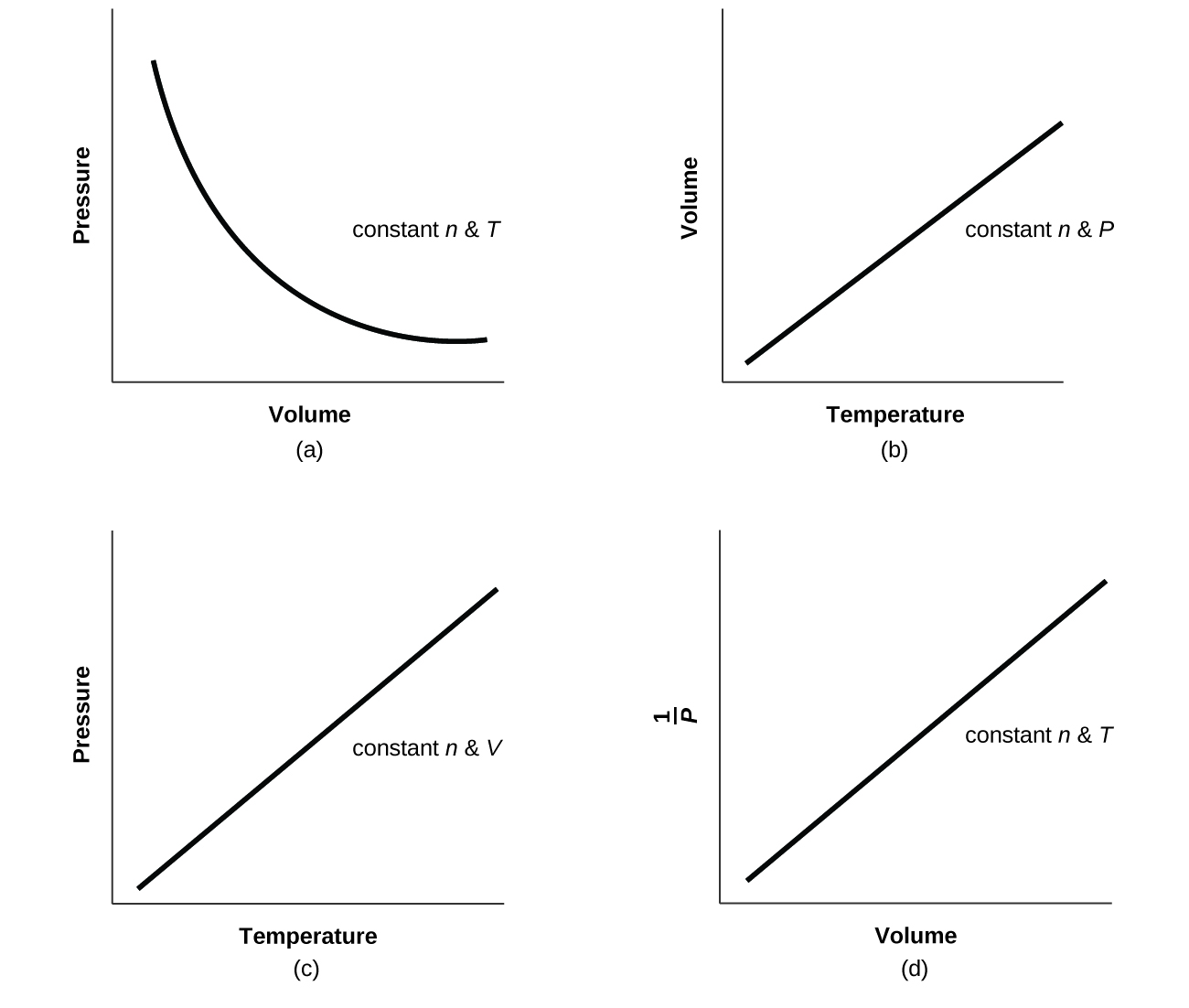
  18. For a given amount of gas showing ideal behavior, draw labeled graphs of:
    1. the variation of P with V
    2. the variation of V with T
    3. the variation of P with T
    4. the variation of [latex]\frac{1}{P}[/latex] with V
  19. A liter of methane gas, CH4, at STP contains more atoms of hydrogen than does a liter of pure hydrogen gas, H2, at STP. Using Avogadro’s law as a starting point, explain why.
  20. The effect of chlorofluorocarbons (such as CCl2F2) on the depletion of the ozone layer is well known. The use of substitutes, such as CH3CH2F(g), for the chlorofluorocarbons, has largely corrected the problem. Calculate the volume occupied by 10.0 g of each of these compounds at STP:
    1. CCl2F2(g)
    2. CH3CH2F(g)
  21. As 1 g of the radioactive element radium decays over 1 year, it produces 1.16 × 1018 alpha particles (helium nuclei). Each alpha particle becomes an atom of helium gas. What is the pressure in pascal of the helium gas produced if it occupies a volume of 125 mL at a temperature of 25 °C?
  22. A balloon that is 100.21 L at 21 °C and 0.981 atm is released and just barely clears the top of Mount Crumpet in British Columbia. If the final volume of the balloon is 144.53 L at a temperature of 5.24 °C, what is the pressure experienced by the balloon as it clears Mount Crumpet?
  23. If the temperature of a fixed amount of a gas is doubled at constant volume, what happens to the pressure?
  24. If the volume of a fixed amount of a gas is tripled at constant temperature, what happens to the pressure?

Answers to Chemistry End of Section Exercises

  1. The cutting edge of a knife that has been sharpened has a smaller surface area than a dull knife. Since pressure is force per unit area, a sharp knife will exert a higher pressure with the same amount of force and cut through material more effectively.
  2. Since pressure is force per unit area, more wheels means there are more area to lower the pressure caused by the weight of the vehicle.
  3. Lying down distributes your weight over a larger surface area, exerting less pressure on the ice compared to standing up. If you exert less pressure, you are less likely to break through thin ice.
  4. 740 torr = 0.97 atm = 740 mm Hg = 99 kPa
  5. 2.2 × 102 kPa
  6. 6.50 millibars = 4.88 torr = 0.650 kPa
  7. Earth: 14.7 lb in–2; Venus: 13.1 × 103 lb in−2
  8. 14.82 MPa = 146.3 atm = 1.112 × 105 torr
  9. (a) 101.39 kPa; (b) 51 torr drop
  10. Barometer is an instrument that is used to measure the atmospheric pressure. A volatile liquid is the one which evaporates at lower temperatures, which can cause error in the measurement due to the vapor produced.
  11. As temperature of a gas increases, pressure will also increase based on the ideal gas law. The volume of the tire can only expand so much before the rubber gives and releases the build up of pressure.
  12. As the bubbles rise, the pressure decreases, so their volume increases as suggested by Boyle’s law.
  13. (a) as one number increases, the other decreases; (b) amount of gas, temperature
  14. (a) The number of particles in the gas increases as the volume increases; (b) temperature, pressure
  15. The curve would be farther to the right and higher up, but the same basic shape.
  16. 12.5 L
  17. a) 16 psi from the P-V graph; b) 15.6 psi using Boyle’s law
  18. 3.40 × 103 torr
  19. 276 K
  20. 12.1 L
  21. 217 L
  22. 103 kPa
  23. 359 K
  24. (a) 7.24 × 10–2 g; (b) 23.1 g; (c) 1.5 × 10–4 g
  25. 5561 L
  26. The tank was filled more than capacity (248 > 220 atm)
  27. 0.57 mol
  28. For a gas exhibiting ideal behavior:
    Four graphs are shown. In a, Volume is on the horizontal axis and Pressure is on the vertical axis. A downward trend with a decreasing rate of change is shown by a curved line. The label n, P cons is shown on the graph. In b, Temperature is on the horizontal axis and Volume is on the vertical axis. An increasing linear trend is shown by a straight line segment. The label n, P cons is shown on the graph. In c, Temperature is on the horizontal axis and Pressure is on the vertical axis. An increasing linear trend is shown by a straight line segment. The label n, P cons is shown on the graph. In d, Volume is on the horizontal axis and 1 divided by Pressure is on the vertical axis. An increasing linear trend is shown by a straight line segment on the graph. The label n, P cons is shown on the graph.
  29. Based on Avogadro’s law, both CH4 and H2 has [latex]\frac{1\;\text{L}}{22.4 \frac{\text{L}}{\text{mol}}} = 0.045\;\text{mol}[/latex] of gas occupying 1 L volume at STP. Since CH4 has four H atoms per molecule and H2 only has two, methane contains more atoms of hydrogen.
  30. (a) 1.85 L CCl2F2; (b) 4.66 L CH3CH2F
  31. 38.2 Pa
  32. 0.644 atm
  33. The pressure also doubles
  34. The pressure decreases by a factor of 3.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

UW-Madison Chemistry 103/104 Resource Book Copyright © by crlandis is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book