32 Hess’s Law (M6Q7)
Introduction
The section introduces to concept of enthalpy as a state function. Using this concept, we will explore and develop a method known as Hess’s Law. This powerful method greatly extends the range of chemical reactions for which we can calculate heat flow. This section includes worked examples, sample problems, and a glossary.
Learning Objectives for Hess’s Law
- Recognize the significance of enthalpy as a state function.
| State Functions | Enthalpy | Standard State | - Apply Hess’s Law to calculate the reaction enthalpy change.
| Hess’s Law |
| Key Concepts and Summary | Glossary | End of Section Exercises |
State Functions
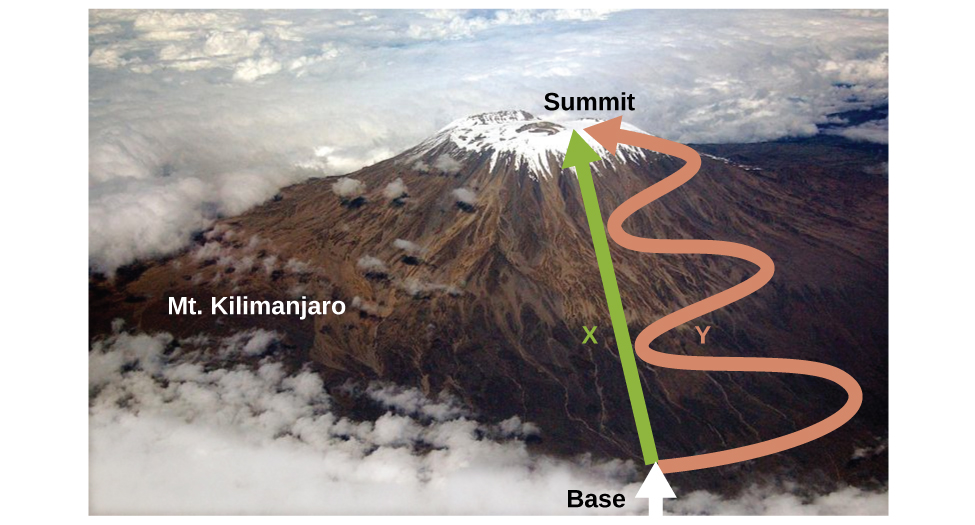
As discussed previously, the relationship between internal energy, heat, and work can be represented as ΔE = q + w. Internal energy is a type of quantity known as a state function (or state variable), whereas heat and work are not state functions. The value of a state function depends only on the state that a system is in, and not on how that state is reached. If a quantity is not a state function, then its value does depend on how the state is reached. An example of a state function is altitude or elevation. If you stand on the summit of Mt. Kilimanjaro, you are at an altitude of 5895 m, and it does not matter whether you hiked there or parachuted there. The distance you traveled to the top of Kilimanjaro, however, is not a state function. You could climb to the summit by a direct route or by a more roundabout, circuitous path (Figure 1). The distances traveled would differ (distance is not a state function) but the elevation reached would be the same (altitude is a state function).
Enthalpy
Chemists ordinarily use a property known as enthalpy (H) to describe the thermodynamics of chemical and physical processes. Enthalpy is a state function. Enthalpy values for specific substances cannot be measured directly; only enthalpy changes for chemical or physical processes can be determined. For processes that take place at constant pressure (a common condition for many chemical and physical changes), the enthalpy change (ΔH) is the heat of reaction at constant pressure (qp). If a chemical or physical process is carried out at constant pressure with the only work done caused by expansion or contraction, then the heat flow (qp) and enthalpy change (ΔH) for the process are equal. We saw this earlier in the module.
The heat given off when you operate a Bunsen burner is equal to the enthalpy change of the methane combustion reaction that takes place, since it occurs at the essentially constant pressure of the atmosphere. Chemists usually perform experiments under normal atmospheric conditions, at constant external pressure with q = ΔH. Determining qp in a calorimeter by measuring the heat exchanged with the surroundings will therefore lead directly to the determination of ΔH for the process taking place in the calorimeter. Using an analogy involving money may help you understand this better. If you withdraw $100 from your bank account (analogous to qp) you can actually count the money you receive. This is what happens in a calorimeter, although it is the Joules of heat that are determined as a reaction occurs. You might not actually know the exact amount of money in your bank account, but your bank balance will have decreased by exactly $100. This is analogous to the enthalpy change. Initial enthalpy values of reactants and final enthalpy values of products, like the bank balance in this example, are not known and nor do they have to be, in order to determine the change or difference between them, ΔH.
The following conventions apply when we use ΔH:
-
Chemists use a thermochemical equation to represent the changes in both matter and energy. In a thermochemical equation, the enthalpy change of a reaction is shown as a ΔH value following the equation for the reaction. This ΔH value indicates the amount of heat associated with the reaction involving the number of moles of reactants and products as shown in the chemical equation. For example, consider this equation:
H2(g) + ½ O2(g) → H2O(l) ΔH = -286 kJ
This equation indicates that when 1 mole of hydrogen gas and ½ mole of oxygen gas at some temperature and pressure react to form 1 mole of liquid water at the same temperature and pressure, 286 kJ of heat are released to the surroundings. If the coefficients of the chemical equation are multiplied by some factor, the enthalpy change must be multiplied by that same factor (ΔH is an extensive property):
(two-fold increase in amounts)
2 H2(g) + O2(g) → 2 H2O(l) ΔH = 2 × (-286 kJ) = -572 kJ(two-fold decrease in amounts)
½ H2(g) + ¼ O2(g) → ½ H2O(l) ΔH = ½ × (-286 kJ) = -143 kJ–
-
The enthalpy change of a reaction depends on the physical state of the reactants and products of the reaction (whether we have gases, liquids, solids, or aqueous solutions), so these must be shown. For example, when 1 mole of hydrogen gas and ½ mole of oxygen gas change to 1 mole of liquid water at the same temperature and pressure, 286 kJ of heat are released. If gaseous water forms, only 242 kJ of heat are released.
H2(g) + ½ O2(g) → H2O(g) ΔH = -242 kJ
-
A negative value of an enthalpy change, ΔH, indicates an exothermic reaction; a positive value of ΔH indicates an endothermic reaction. If the direction of a chemical equation is reversed, the arithmetic sign of its ΔH is changed (a process that is endothermic in one direction is exothermic in the opposite direction).
H2O(l) → H2(g) + ½ O2(g) ΔH = -1 × (-286 kJ) = 286 kJ
Example 1
Measurement of an Enthalpy Change
When 0.0500 mol of HCl(aq) reacts with 0.0500 mol of NaOH(aq) to form 0.0500 mol of NaCl(aq), 2.9 kJ of heat are produced (released). What is ΔH, the enthalpy change, per 1 mole of hydrochloric acid (HCl)?
Solution
For the reaction of 0.0500 mol acid (HCl), q = −2.9 kJ. This ratio [latex]\frac{-2.9\;\text{kJ}}{0.0500 \;\text{mol HCl}}[/latex] can be used as a conversion factor to find the heat produced when 1 mole of HCl reacts:
The enthalpy change when 1 mole of HCl reacts is −58 kJ. Since that is the number of moles in the chemical equation, we write the thermochemical equation as:
Check Your Learning
When 1.34 g Zn(s) reacts with 60.0 mL of 0.750 M HCl(aq), 3.14 kJ of heat are produced. Determine the enthalpy change per mole of zinc reacting for the reaction:
Answer:
Zn is the limiting reagent
ΔH = −153 kJ
Be sure to take both stoichiometry and limiting reactants into account when determining the ΔH for a chemical reaction.
Example 2
Another Example of the Measurement of an Enthalpy Change
A gummy bear contains 2.67 g sucrose, C12H22O11. When it reacts with 7.19 g potassium chlorate, KClO3, 43.7 kJ of heat are produced (released). Determine the enthalpy change for the reaction
Solution
We have 2.67 g × [latex]\frac{1 \;\text{mol}}{342.3 \;\rule[0.25ex]{0.55em}{0.1ex}\hspace{-0.55em}\text{g}}[/latex] = 0.00780 mol C12H22O11 available, and 7.19 g × [latex]\frac{1 \;\text{mol}}{122.5 \;\rule[0.25ex]{0.55em}{0.1ex}\hspace{-0.55em}\text{g}}[/latex] = 0.0587 mol KClO3 available.
0.0587 mol KClO3 × [latex]\frac{1 \;\text{mol C}_{12} \text{H}_{22} \text{O}_{11}}{8 \;\text{mol KClO}_3}[/latex] = 0.00734 mol C12H22O11 is needed; C12H22O11 is the excess reactant and KClO3 is the limiting reactant.
The reaction uses 8 mol KClO3, and the conversion factor is [latex]\frac{-43.7\;\text{kJ}}{0.0587 \;\text{mol KClO}_3}[/latex], so we have ΔH = 8 mol × [latex]\frac{-43.7 \;\text{kJ}}{0.0587 \;\text{mol KClO}_3}[/latex] = -5960 kJ. The enthalpy change for this reaction is −5960 kJ, and the thermochemical equation is:
Check Your Learning
When 1.42 g of iron reacts with 1.80 g of chlorine, 3.22 g of FeCl2(s) and 8.60 kJ of heat is produced. What is the enthalpy change for the reaction when 1 mole of FeCl2(s) is produced?
Answer:
ΔH = −338 kJ
Standard State
Enthalpy changes are typically tabulated for reactions in which both the reactants and products are at the same conditions. A standard state is a commonly accepted set of conditions used as a reference point for the determination of properties under other different conditions. For chemists, the IUPAC standard state refers to materials under a pressure of 1 bar and solutions at 1 M, and does not specify a temperature. Many thermochemical tables list values with a standard state of 1 atm. Because the ΔH of a reaction changes very little with such small changes in pressure (1 bar = 0.987 atm), ΔH values (except for the most precisely measured values) are essentially the same under both sets of standard conditions. We will include a superscripted “o” in the enthalpy change symbol to designate standard state. Thermodynamic data is given for the standard states and a specified temperature which is almost always 298.15 K. In this text, if the temperature is not provided for a ΔHo value, you may assume the temperature is 298.15 K. (The symbol ΔH is used to indicate an enthalpy change for a reaction occurring under nonstandard conditions.)
The enthalpy changes for many types of chemical and physical processes are available in the reference literature, including those for combustion reactions, phase transitions, and formation reactions. As we discuss these quantities, it is important to pay attention to the extensive nature of enthalpy and enthalpy changes. Since the enthalpy change for a given reaction is proportional to the amounts of substances involved, it may be reported on that basis (i.e., as the ΔH for specific amounts of reactants). However, we often find it more useful to divide one extensive property (ΔH) by another (amount of substance), and report a per-amount intensive value of ΔH, often “normalized” to a per-mole basis. (Note that this is similar to determining the intensive property of specific heat from the extensive of property heat capacity.)
Chemistry in Real Life: Emerging Algae-Based Energy Technologies (Biofuels)
As reserves of fossil fuels diminish and become more costly to extract, the search is ongoing for replacement fuel sources for the future. Among the most promising biofuels are those derived from algae (Figure 2). The species of algae used are nontoxic, biodegradable, and among the world’s fastest growing organisms. About 50% of algal weight is oil, which can be readily converted into fuel such as biodiesel. Algae can yield 26,000 gallons of biofuel per hectare—much more energy per acre than other crops. Some strains of algae can flourish in brackish water that is not usable for growing other crops. Algae can produce biodiesel, biogasoline, ethanol, butanol, methane, and even jet fuel.

According to the US Department of Energy, only 39,000 square kilometers (about 0.4% of the land mass of the US or less than of the area used to grow corn) can produce enough algal fuel to replace all the petroleum-based fuel used in the US. The cost of algal fuels is becoming more competitive—for instance, the US Air Force is producing jet fuel from algae at a total cost of under 5 dollars per gallon.[1]The process used to produce algal fuel is as follows: grow the algae (which use sunlight as their energy source and CO2 as a raw material), harvest the algae, extract the fuel compounds (or precursor compounds), process as necessary (e.g., perform a transesterification reaction to make biodiesel), purify, and distribute (Figure 3).
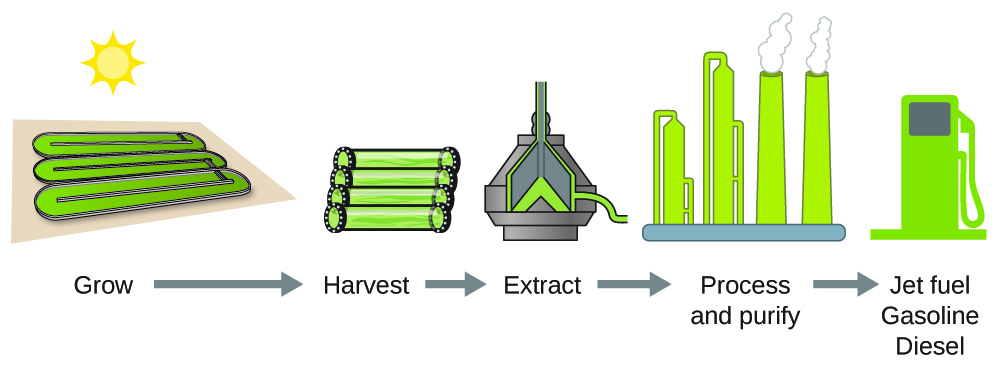

Learn more about the process of creating algae biofuel.
Hess’s Law
There are two ways to determine the enthalpy changes involved in a chemical change: measure it experimentally, or calculate it from other experimentally determined enthalpy changes. Some reactions are difficult, if not impossible, to undertake in the controlled conditions of a calorimeter. Even when a reaction is not hard to perform or measure, it is convenient to be able to determine the energy changes involved in a reaction without having to perform an experiment.
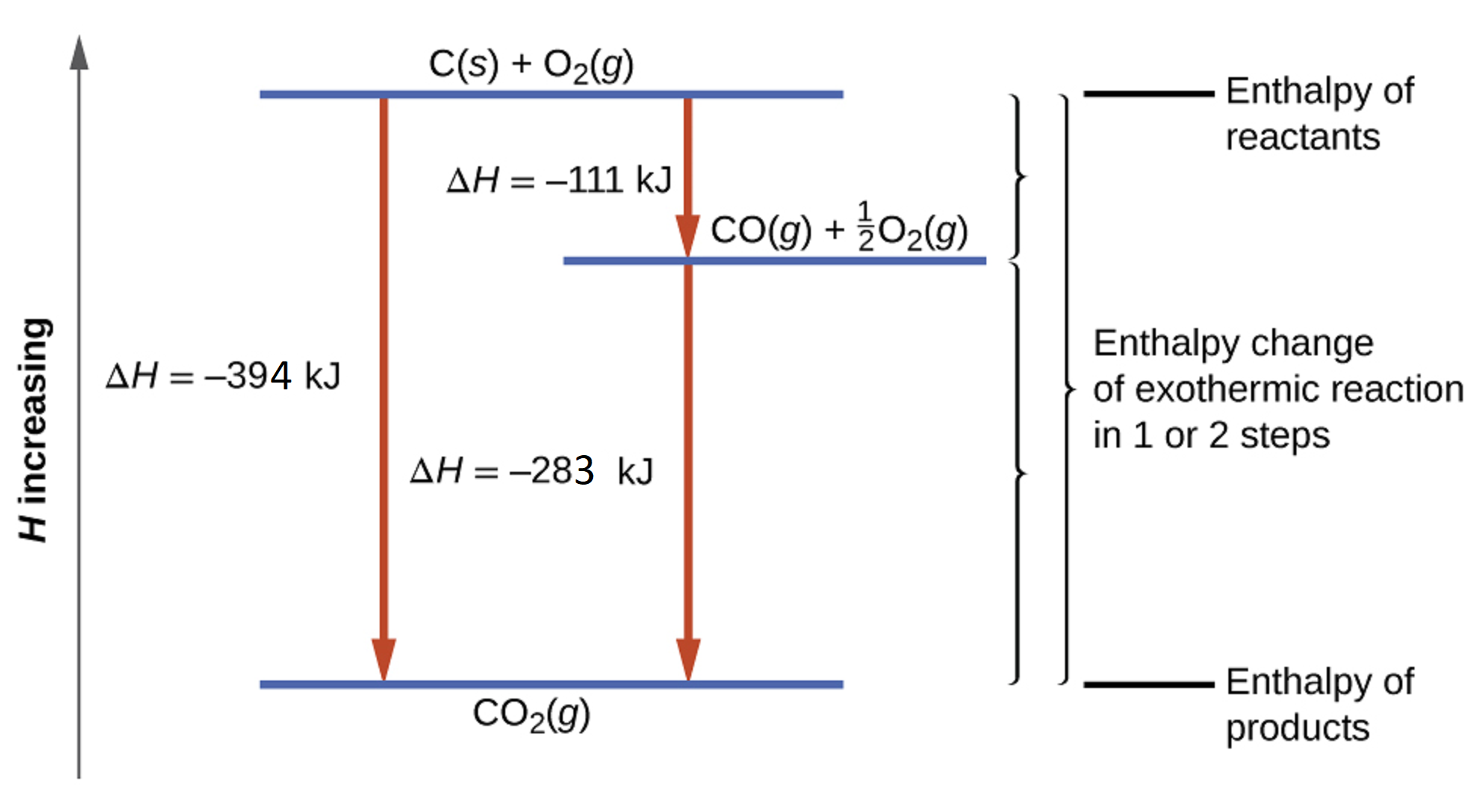
This type of calculation usually involves the use of Hess’s law, which states: if a process can be written as the sum of several stepwise processes, the enthalpy change of the total process equals the sum of the enthalpy changes of the various steps. Hess’s law is valid because enthalpy is a state function: enthalpy changes depend only on where a chemical process starts and ends, but not on the path it takes from start to finish. For example, we can think of the reaction of carbon with oxygen to form carbon dioxide as occurring either directly or by a two-step process. The direct process is written:
C(s) + O2(g) → CO2(g) ΔH° = -394 kJ
In the two-step process, first carbon monoxide is formed:
C(s) + ½ O2(g) → CO(g) ΔH° = -111 kJ
Then, carbon monoxide reacts further to form carbon dioxide:
CO(g) + ½ O2(g) → CO2(g) ΔH° = -283 kJ
The equation describing the overall reaction is the sum of these two chemical changes:
Step 1: C(s) + ½ O2(g) → CO(g)
Step 2: CO(g) + ½ O2(g) → CO2(g)
—————————————————————————————————
Sum: C(s) + ½ O2(g) + CO(g) + ½ O2(g) → CO(g) + CO2(g)
Because the CO produced in Step 1 is consumed in Step 2, the net change is:
C(s) + O2(g) → CO2(g)
According to Hess’s law, the enthalpy change of the reaction will equal the sum of the enthalpy changes of the steps. We can apply the data from the experimental enthalpies in Appendix F to find the enthalpy change of the entire reaction from its two steps (we will discuss how to use Appendix F in the next section):
Step 2: CO(g) + ½ O2(g) → CO2(g) ΔH° = -283 kJ
—————————————————————————————————
Sum: C(s) + O2(g) → CO2(g) ΔH° = -394 kJ
The result is shown in Figure 4. We see that ΔH of the overall reaction is the same whether it occurs in one step or two. This finding (overall ΔH for the reaction = sum of ΔH values for reaction “steps” in the overall reaction) is true in general for chemical and physical processes.
Before we further practice using Hess’s law, let us recall two important features of ΔH.
-
ΔH is directly proportional to the quantities of reactants or products. For example, the enthalpy change for the reaction forming 1 mole of NO2(g) is +33.2 kJ:
½ N2(g) + O2(g) → NO2(g) ΔH = +33.2 kJWhen 2 moles of NO2 (twice as much) are formed, the ΔH will be twice as large:
N2(g) + 2 O2(g) → 2 NO2(g) ΔH = +66.4 kJ
In general, if we multiply or divide an equation by a number, then the enthalpy change should also be multiplied or divided by the same number.
-
ΔH for a reaction in one direction is equal in magnitude and opposite in sign to ΔH for the reaction in the reverse direction. For example, given that:
H2(g) + Cl2(g) → 2 HCl(g) ΔH = -184.6 kJThen, for the “reverse” reaction, the enthalpy change is also “reversed”:
2 HCl(g) → H2(g) + Cl2(g) ΔH = +184.6 kJ
Example 3
Stepwise Calculation of ΔH°rxn Using Hess’s Law
For the reaction:
Fe(s) + [latex]\frac{3}{2}[/latex] Cl2(g) → FeCl3(s) ΔH°rxn = ?
Determine the enthalpy of the reaction, ΔH°rxn, of FeCl3(s) from the enthalpy changes of the following two-step process that occurs under standard state conditions:
FeCl2(s) + [latex]\frac{1}{2}[/latex] Cl2(g) → FeCl3(s) ΔH°rxn = -57.7 kJ
Solution
Looking at the reactions, we see that the reaction for which we want to find ΔH° is the sum of the two reactions with known ΔH values, so we must sum their ΔHs:
FeCl2(s) + [latex]\frac{1}{2}[/latex] Cl2(g) → FeCl3(s) ΔH° = -57.7 kJ
———————————————————————————
Fe(s) + [latex]\frac{3}{2}[/latex] Cl2(g) → FeCl3(s) ΔH° = -399.5 kJ
The enthalpy of reaction, ΔH°rxn, of FeCl3(s) is −399.5 kJ/mol.
Check Your Learning
Calculate ΔH for the process:
from the following information:
NO(g) + ½ O2(g) → NO2(g) ΔH = -57.06 kJ
Answer:
+66.4 kJ
Here is a less straightforward example that illustrates the thought process involved in solving many Hess’s law problems. It shows how we can find many standard enthalpies if they are difficult to determine experimentally.
Example 4
A More Challenging Problem Using Hess’s Law
Chlorine monofluoride can react with fluorine to form chlorine trifluoride:
(i)
ClF(g) + F2(g) → ClF3(g) ΔH° = ?
Use the reactions here to determine the ΔH° for reaction (i):
(ii)
2 OF2(g) → O2(g) + 2 F2(g) ΔH°(ii) = -49.4 kJ
(iii)
2 ClF(g) + O2(g) → Cl2O(g) + OF2(g) ΔH°(iii) = +205.6 kJ
(iv)
ClF3(g) + O2(g) → [latex]\frac{1}{2}[/latex] Cl2O(g) + [latex]\frac{3}{2}[/latex] OF2(g) ΔH°(iii) = +266.7 kJ
Solution
Our goal is to manipulate and combine reactions (ii), (iii), and (iv) such that they add up to reaction (i). Going from left to right in (i), we first see that ClF(g) is needed as a reactant. This can be obtained by multiplying reaction (iii) by ½, which means that the ΔH° change is also multiplied by ½:
Next, we see that F2 is also needed as a reactant. To get this, reverse and halve reaction (ii), which means that the ΔH° changes sign and is halved:
To get ClF3 as a product, reverse (iv), changing the sign of ΔH°:
Now check to make sure that these reactions add up to the reaction we want:
ClF(g) + [latex]\frac{1}{2}[/latex] O2(g) → [latex]\frac{1}{2}[/latex] Cl2O(g) + [latex]\frac{1}{2}[/latex] OF2(g) ΔH° = +102.8 kJ
[latex]\frac{1}{2}[/latex] O2(g) + F2(g) → OF2(g) ΔH° = +24.7 kJ
[latex]\frac{1}{2}[/latex] Cl2O(g) + [latex]\frac{3}{2}[/latex] OF2(g) → ClF3(g) + O2(g) ΔH° = -266.7 kJ
——————————————————————————————————————
ClF(g) + F2(g) → ClF3(g) ΔH° = -139.2 kJ
Reactants [latex]\frac{1}{2}[/latex] O2 and [latex]\frac{1}{2}[/latex] O2 cancel out product O2; product [latex]\frac{1}{2}[/latex] Cl2O cancels reactant [[latex]\frac{1}{2}[/latex] Cl2O; and reactant [latex]\frac{3}{2}[/latex] OF2 is cancelled by products [latex]\frac{1}{2}[/latex] OF2 and OF2. This leaves only reactants ClF(g) and F2(g) and product ClF3(g), which are what we want. Since summing these three modified reactions yields the reaction of interest, summing the three modified ΔH° values will give the desired ΔH°:
Check Your Learning
Aluminum chloride can be formed from its elements:
(i)
2 Al(s) + 3 Cl2(g) → 2 AlCl3(s) ΔH° = ?
Use the reactions here to determine the ΔH° for reaction (i):
(ii)
HCl(g) → HCl(aq) ΔH°(ii) = -74.8 kJ
(iii)
H2(g) + Cl2(g) → 2 HCl(g) ΔH°(iii) = -185 kJ
(iv)
AlCl3(aq) → AlCl3(s) ΔH°(iv) = +323 kJ
(v)
2 Al(s) + 6 HCl(aq) → 2 AlCl3(aq) + 3 H2(g) ΔH°(v) = -1049 kJ
Answer:
−1407 kJ
Key Concepts and Summary
Enthalpy is a state function, meaning it only depends on the initial and final conditions, not the path between the two. The enthalpy change of a reaction can be measured since heat flow at constant pressure (qp = ΔH). The enthalpy change of a reaction can also be calculated using Hess’s law: If a process can be written as the sum of several stepwise processes, the enthalpy change of the total process equals the sum of the enthalpy changes of the various steps. Enthalpy values are tabulated at standard state conditions: 1 bar of pressure, and solutions at 1 molar concentrations, usually at a temperature of 298.15 K. We can use these tabulated enthalpy values and Hess’s law to determine the enthalpy change of reactions that are too difficult or dangerous to measure directly.
Glossary
- enthalpy change (ΔH)
- heat released or absorbed by a system under constant pressure during a chemical or physical process
Hess’s law
If a process can be represented as the sum of several steps, the enthalpy change of the process equals the sum of the enthalpy changes of the steps
- standard state
-
- set of physical conditions as accepted as common reference conditions for reporting thermodynamic properties; 1 bar of pressure, and solutions at 1 molar concentrations, usually at a temperature of 298.15 K
- state function
- property depending only on the state of a system, and not the path taken to reach that state
Chemistry End of Section Exercises
- The following sequence of reactions occurs in the commercial production of aqueous nitric acid. Determine the total energy change for the production of one mole of aqueous nitric acid by this process.
4NH3(g) + 5O2(g) ⟶ 4NO(g) + 6H2O(l) ΔH = -907 kJ 2NO(g) + O2(g) ⟶ 2NO2(g) ΔH = -113 kJ 3NO2(g) + H2O(l) ⟶ 2HNO3(aq) + NO(g) ΔH = -139 kJ - Which produces more heat?
Os(s) + 2O2(g) ⟶ OsO4(s) OR Os(s) + 2O2(g) ⟶ OsO4(g)
The phase change of OsO4: OsO4(s) ⟶ OsO4(g) ΔH = 56.4 kJ - Calculate ΔH°298 for the process: Sb(s) + [latex]\frac{5}{2}[/latex]Cl2(g) ⟶ SbCl5(g) from the following information:
Sb(s) + [latex]\frac{3}{2}[/latex]Cl2(g) ⟶ SbCl3(g) ΔH°298 = -314 kJ SbCl3(g) + Cl2(g) ⟶ SbCl5(g) ΔH°298 = -80 kJ - Calculate ΔH°298 for the process: Zn(s) + S(s) + 2O2(g) ⟶ ZnSO4(s) from the following information:
Zn(s) + S(s) ⟶ ZnS(s) ΔH°298 = -206.0 kJ ZnS(s) + 2O2(g) ⟶ ZnSO4(s) ΔH°298 = -776.8 kJ - Calculate ΔH for the process Hg2Cl2(s) ⟶ 2Hg(l) + Cl2(g) from the following information:
Hg(l) + Cl2(g) ⟶ HgCl2(s) ΔH = -224 kJ Hg(l) + HgCl2(s) ⟶ Hg2Cl2(s) ΔH = -41.2 kJ - Explain how the enthalpy change for a reaction of 1 mol HCl and 1 mol NaOH differs from the enthalpy change for a reaction of 0.5 mol HCl and 0.5 mole NaOH.
- When 100 mL of 0.2 M NaCl(aq) reacts with 100 mL of 0.2 M AgNO3(aq), 1.34 x 103 J are released. Calculate ΔH in kJ/mol of AgNO3(aq) for the reaction:
NaCl(aq) + AgNO3(aq) → AgCl(s) + NaNO3(aq)
- When 3.21 g of solid ammonium nitrate dissolves in a beaker containing 50.0 g of water, 1.33 kJ is absorbed from the surroundings, making the beaker cold. Calculate the enthalpy of solution (ΔH for the dissolution) per mole of NH4NO3.
- When 2.50 g of methane burns in oxygen, 125 kJ of heat is produced. What is the enthalpy of combustion per mole of methane under these conditions?
- The enthalpy of combustion of hard coal averages −35 kJ/g, that of gasoline, 1.28 × 105 kJ/gal. How many kilograms of hard coal provide the same amount of heat as is available from 1.0 gallon of gasoline? Assume that the density of gasoline is 0.692 g/mL (the same as the density of isooctane).
Answers to Chemistry End of Section Exercises
- −495 kJ/mol
- Os(s) + 2O2(g) ⟶ OsO4(s)
- −394 kJ
- -983 kJ
- 265 kJ
- The heat (kJ) released from a 1 mol HCl and 1 mol NaOH reaction is twice as large as the heat released from a 0.5 mol HCl and 0.5 mol NaOH reaction. The same ratio applies for the enthalpy change ratio of both reactions.
- 67 kJ/mol
- 33 kJ/mol
- 802 kJ/mol
- 3.7 kg

