17 Empirical Formula (M4Q4)

Introduction

The section explores empirical formulas and the use of combustion to analyze a compound. This section includes worked examples, sample problems, and a glossary. 

Learning Objectives for Empirical Formulas

| Key Concepts and Summary | Key Equations | Glossary | End of Section Exercises |

Determination of Empirical Formulas

As previously mentioned, the most common approach to determining a compound’s chemical formula is to first measure the masses of its constituent elements. However, we must keep in mind that chemical formulas represent the relative numbers, not masses, of atoms in the substance. Therefore, any experimentally derived data involving mass must be used to derive the corresponding numbers of atoms in the compound. To accomplish this, we can use molar masses to convert the mass of each element to a number of moles. We then consider the moles of each element relative to each other, converting these numbers into a whole-number ratio that can be used to derive the empirical formula of the substance. Consider a sample of compound determined to contain 1.71 g C and 0.287 g H. The corresponding numbers of atoms (in moles) are:

1.71 g C × [latex]\frac{1 \;\text{mol C}}{12.01 \;\text{g C}}[/latex]  =  0.142 mol C

0.287 g H × [latex]\frac{1 \;\text{mol H}}{1.008 \;\text{g H}}[/latex]  =  0.284 mol H

Thus, we can accurately represent this compound with the formula C0.142H0.248. Of course, per accepted convention, formulas contain whole-number subscripts, which can be achieved by dividing each subscript by the smaller subscript:

[latex]\text{C}_{\frac{0.142}{0.142}} \; \text{H}_{\frac{0.248}{0.142}}[/latex] or CH2

(Recall that subscripts of “1” are not written but rather assumed if no other number is present.)

The empirical formula for this compound is thus CH2. This may or not be the compound’s molecular formula as well; however, we would need additional information to make that determination (as discussed later in this section).

Consider as another example a sample of compound determined to contain 5.31 g Cl and 8.40 g O. Following the same approach yields a tentative empirical formula of:

Cl0.150O0.525  =  [latex]\text{Cl}_{\frac{0.150}{0.150}} \; \text{O}_{\frac{0.525}{0.150}}[/latex]  =  ClO3.5

In this case, dividing by the smallest subscript still leaves us with a decimal subscript in the empirical formula. To convert this into a whole number, we must multiply each of the subscripts by two, retaining the same atom ratio and yielding Cl2O7 as the final empirical formula.

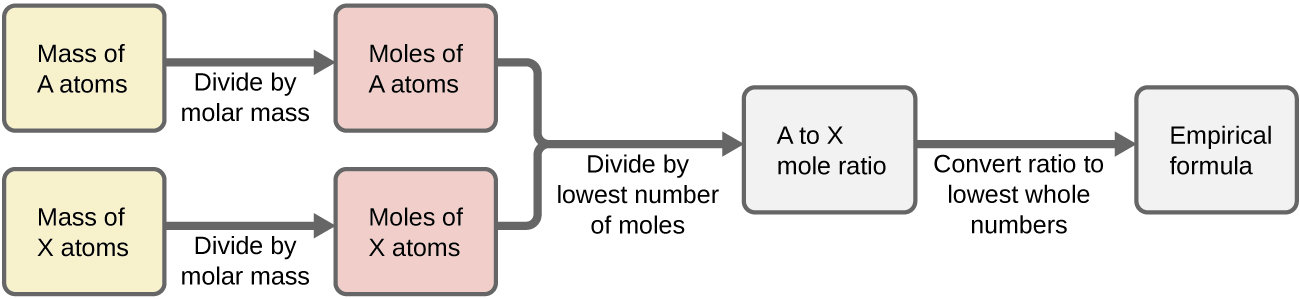
In summary, empirical formulas are derived from experimentally measured element masses by:

  1. Deriving the number of moles of each element from its mass
  2. Dividing each element’s molar amount by the smallest molar amount to yield subscripts for a tentative empirical formula
  3. Multiplying all coefficients by an integer, if necessary, to ensure that the smallest whole-number ratio of subscripts is obtained

Figure 1 outlines this procedure in flow chart fashion for a substance containing elements A and X.

A flow chart is shown that is composed of six boxes, two of which are connected together by a right facing arrow and located above two more that are also connected by a right-facing arrow. These two rows of boxes are connected vertically by a line that leads to a right-facing arrow and the last two boxes, connected by a final right facing arrow. The first two upper boxes have the phrases, “Mass of A atoms” and “Moles of A atoms” respectively, while the arrow that connects them has the phrase, “Divide by molar mass,” written below it. The second two bottom boxes have the phrases, “Mass of X atoms” and “Moles of X atoms” respectively, while the arrow that connects them has the phrase, “Divide by molar mass” written below it. The arrow that connects the upper and lower boxes to the last two boxes has the phrase “Divide by lowest number of moles” written below it. The last two boxes have the phrases, “A to X mole ratio” and “Empirical formula” respectively, while the arrow that connects them has the phrase, “Convert ratio to lowest whole numbers” written below it.
Figure 1. The empirical formula of a compound can be derived from the masses of all elements in the sample.

Example 1

Determining a Compound’s Empirical Formula from the Masses of Its Elements

A sample of the black mineral hematite (Figure 2), an oxide of iron found in many iron ores, contains 34.97 g of iron and 15.03 g of oxygen. What is the empirical formula of hematite?

Two rounded, smooth black stones are shown.
Figure 2. Hematite is an iron oxide that is used in jewelry. (credit: Mauro Cateb)

Solution
For this problem, we are given the mass in grams of each element. Begin by finding the moles of each:

34.97 g Fe × [latex]\frac{1\;\text{mol Fe}}{55.85\;\text{g Fe}}[/latex]  =  0.6261 mol Fe

 

15.03 g O × [latex]\frac{1\;\text{mol O}}{16.00\;\text{g O}}[/latex]  =  0.9394 mol O

Next, derive the iron-to-oxygen molar ratio by dividing by the lesser number of moles:

[latex]\frac{0.6261}{0.6261}[/latex]  =  1.000 mol Fe

 

[latex]\frac{0.9394}{0.6261}[/latex]  =  1.500 mol O

The ratio is 1.000 mol of iron to 1.500 mol of oxygen (Fe1O1.5). Finally, multiply the ratio by two to get the smallest possible whole number subscripts while still maintaining the correct iron-to-oxygen ratio:

2 × Fe1O1.5  =  Fe2O3

The empirical formula is Fe2O3.

Check Your Learning
What is the empirical formula of a compound if a sample contains 0.130 g of nitrogen and 0.370 g of oxygen?

Answer:

N2O5

 

For additional worked examples illustrating the derivation of empirical formulas, watch the brief video clip.

Deriving Empirical Formulas from Percent Composition

Finally, with regard to deriving empirical formulas, consider instances in which a compound’s percent composition is available rather than the absolute masses of the compound’s constituent elements. In such cases, the percent composition can be used to calculate the masses of elements present in any convenient mass of compound; these masses can then be used to derive the empirical formula in the usual fashion. Since the scale for percentages is 100, it is most convenient to assume a 100 g sample to calculate the mass of each element.

Example 2

Determining an Empirical Formula from Percent Composition

The bacterial fermentation of grain to produce ethanol forms a gas with a percent composition of 27.29% C and 72.71% O (Figure 3). What is the empirical formula for this gas?

A picture is shown of four copper-colored industrial containers with a large pipe connecting to the top of each one.
Figure 3. An oxide of carbon is removed from these fermentation tanks through the large copper pipes at the top. (credit: “Dual Freq”/Wikimedia Commons)

Solution
Since the scale for percentages is 100, it is most convenient to calculate the mass of elements present in a sample weighing 100 g. The calculation is “most convenient” because, per the definition for percent composition, the mass of a given element in grams is numerically equivalent to the element’s mass percentage. This numerical equivalence results from the definition of the “percentage” unit, whose name is derived from the Latin phrase per centum meaning “by the hundred.” Considering this definition, the mass percentages provided may be more conveniently expressed as fractions:

27.29% C  =  [latex]\frac{27.29\;\text{g C}}{100\;\text{g compound}}[/latex]

 

72.71% O  =  [latex]\frac{72.71\;\text{g O}}{100\;\text{g compound}}[/latex]

The molar amounts of carbon and hydrogen in a 100-g sample are calculated by dividing each element’s mass by its molar mass:

27.29% C × [latex]\frac{\text{mol C}}{12.01\;\text{g}}[/latex]  =  2.272 mol C

 

72.71% O × [latex]\frac{\text{mol O}}{16.00\;\text{g}}[/latex]  =  4.544 mol O

Coefficients for the tentative empirical formula are derived by dividing each molar amount by the lesser of the two:

[latex]\frac{2.272\;\text{mol C}}{2.272\;\text{mol}}[/latex]  =  1 C

 

[latex]\frac{4.544\;\text{mol O}}{2.272\;\text{mol}}[/latex]  =  2 O

Since the resulting ratio is one carbon to two oxygen atoms, the empirical formula is CO2.

Check Your Learning
What is the empirical formula of a compound containing 40.0% C, 6.71% H, and 53.28% O?

Answer:

CH2O

Derivation of Molecular Formulas

Recall that empirical formulas are symbols representing the relative numbers of a compound’s elements. Determining the absolute numbers of atoms that compose a single molecule of a covalent compound requires knowledge of both its empirical formula and its molecular mass or molar mass. These quantities may be determined experimentally by various measurement techniques. Molecular mass, for example, is often derived from the mass spectrum of the compound (see discussion of this technique in the section on mass spectrometry of molecules from earlier in the semester). Molar mass can be measured by a number of experimental methods, many of which will be introduced in later chapters of this text.

Molecular formulas are derived by comparing the compound’s molecular or molar mass to its empirical formula mass. As the name suggests, an empirical formula mass is the sum of the average atomic masses of all the atoms represented in an empirical formula. If we know the molecular (or molar) mass of the substance, we can divide this by the empirical formula mass in order to identify the number of empirical formula units per molecule, which we designate as n:

[latex]\frac{\text{molecular or molar mass (amu or} \;\frac{\text{g}}{\text{mol}})}{\text{empirical formula mass (amu or} \;\frac{\text{g}}{\text{mol}})}[/latex]  =  n formula units/molecule

The molecular formula is then obtained by multiplying each subscript in the empirical formula by n, as shown by the generic empirical formula AxBy:

(AxBy)n  =  AnxBny

For example, consider a covalent compound whose empirical formula is determined to be CH2O. The empirical formula mass for this compound is approximately 30 amu (the sum of 12 amu for one C atom, 2 amu for two H atoms, and 16 amu for one O atom). If the compound’s molecular mass is determined to be 180 amu, this indicates that molecules of this compound contain six times the number of atoms represented in the empirical formula:

[latex]\frac{180 \;\text{amu/molecule}}{30\;\frac{\text{amu}}{\text{formula unit}}}[/latex]  =  6 formula units/molecule

Molecules of this compound are then represented by molecular formulas whose subscripts are six times greater than those in the empirical formula:

(CH2O)6  =  C6H12O6

Note that this same approach may be used when the molar mass (g/mol) instead of the molecular mass (amu) is used. In this case, we are merely considering one mole of empirical formula units and molecules, as opposed to single units and molecules.

Example 3

Determination of the Molecular Formula for Nicotine

Nicotine, an alkaloid in the nightshade family of plants that is mainly responsible for the addictive nature of cigarettes, contains 74.02% C, 8.710% H, and 17.27% N. If 40.57 g of nicotine contains 0.2500 mol nicotine, what is the molecular formula?

Solution
Determining the molecular formula from the provided data will require comparison of the compound’s empirical formula mass to its molar mass. As the first step, use the percent composition to derive the compound’s empirical formula. Assuming a convenient, a 100-g sample of nicotine yields the following molar amounts of its elements:

(74.02 g C)([latex]\frac{1\;\text{mol C}}{12.01\;\text{g C}}[/latex])  =  6.163 mol C

 

(8.710 g H)([latex]\frac{1\;\text{mol H}}{1.01\;\text{g H}}[/latex])  =  8.624 mol H

 

(17.27 g N)([latex]\frac{1\;\text{mol N}}{14.01\;\text{g N}}[/latex])  =  1.233 mol N

Next, we calculate the molar ratios of these elements relative to the least abundant element, N.

[latex]\frac{6.163\ \text{mol C}}{1.233\ \text{mol N}}[/latex]  ≅  5

[latex]\frac{8.264\ \text{mol H}}{1.233\ \text{mol N}}[/latex]  ≅  7

[latex]\frac{1.233\ \text{mol N}}{1.233\ \text{mol N}}[/latex]  ≅  1

The C-to-N and H-to-N molar ratios are adequately close to whole numbers, and so the empirical formula is C5H7N. The empirical formula mass for this compound is therefore 81.13 amu/formula unit, or 81.13 g/mol formula unit.

We calculate the molar mass for nicotine from the given mass and molar amount of compound:

[latex]\frac{40.57 \;\text{g nicotine}}{0.2500 \;\text{mol nicotine}}  = \frac{162.3 \;\text{g}}{1\;\text{mol}}[/latex]

Comparing the molar mass and empirical formula mass indicates that each nicotine molecule contains two formula units:

[latex]\frac{162.3 \;\text{g/mol}}{81.13 \;\frac{\text{g}}{\text{formula unit}}}[/latex]  =  2 formula units/molecule

Thus, we can derive the molecular formula for nicotine from the empirical formula by multiplying each subscript by two:

(C5H7N)2  =  C10H14N2

Check Your Learning
What is the molecular formula of a compound with a percent composition of 49.47% C, 5.201% H, 28.84% N, and 16.48% O, and a molecular mass of 194.2 amu?

Answer:

C8H10N4O2

Combustion Analysis

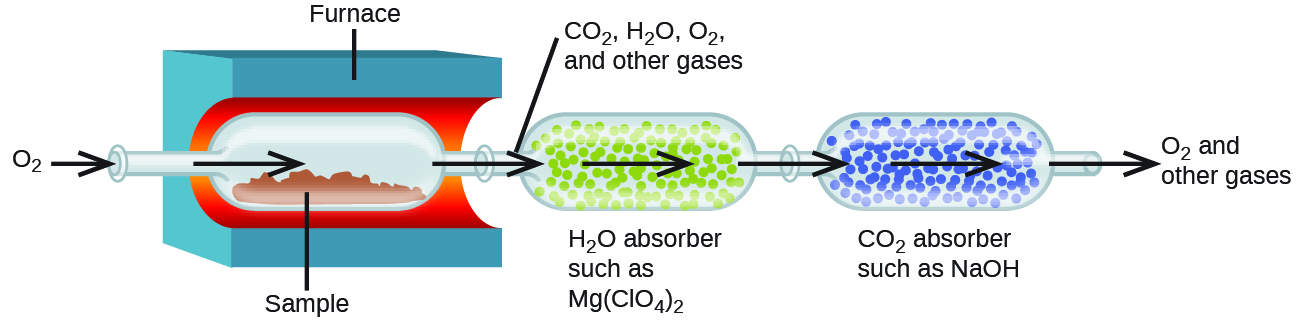
The elemental composition of hydrocarbons and related compounds may be determined via a method known as combustion analysis. In a combustion analysis, a weighed sample of the compound is heated to a high temperature under a stream of oxygen gas, resulting in its complete combustion to yield gaseous products of known identities. The complete combustion of hydrocarbons, for example, will yield carbon dioxide and water as the only products. The gaseous combustion products are swept through separate, preweighed collection devices containing compounds that selectively absorb each product (Figure 4). The mass increase of each device corresponds to the mass of the absorbed product and may be used in an appropriate stoichiometric calculation to derive the mass of the relevant element.

This diagram shows an arrow pointing from O subscript 2 into a tube that leads into a vessel containing a red material, labeled “Sample.” This vessel is inside a blue container with a red inner lining which is labeled “Furnace.” An arrow points from the tube to the right into the vessel above the red sample material. An arrow leads out of this vessel through a tube into a second vessel outside the furnace. An line points from this tube to a label above the diagram that reads “C O subscript 2, H subscript 2 O, O subscript 2, and other gases.” Many small green spheres are visible in the second vessel which is labeled below, “H subscript 2 O absorber such as M g ( C l O subscript 4 ) subscript 2.” An arrow points to the right through the vessel, and another arrow points right heading out of the vessel through a tube into a third vessel. The third vessel contains many small blue spheres. It is labeled “C O subscript 2 absorber such as N a O H.” An arrow points right through this vessel, and a final arrow points out of a tube at the right end of the vessel. Outside the end of this tube at the end of the arrow is the label, “O subscript 2 and other gases.”
Figure 4. This schematic diagram illustrates the basic components of a combustion analysis device for determining the carbon and hydrogen content of a sample.

Example 4

Combustion Analysis

Polyethylene is a hydrocarbon (with formula CxHy) polymer used to produce food-storage bags and many other flexible plastic items. A combustion analysis of a 0.00126-g sample of polyethylene yields 0.00394 g of CO2 and 0.00161 g of H2O. What is the empirical formula of polyethylene?

Solution
The primary assumption in this exercise is that all the carbon in the sample combusted is converted to carbon dioxide, and all the hydrogen in the sample is converted to water:

CxHy(s)   +  excess O2(g)   →   x CO2(g)  +  [latex]\frac{y}{2}[/latex] H2O(g)

Note that a balanced equation is not necessary for the task at hand. To derive the empirical formula of the compound, only the subscripts x and y are needed.

First, calculate the molar amounts of carbon and hydrogen in the sample, using the provided masses of the carbon dioxide and water, respectively. With these molar amounts, the empirical formula for the compound may be written as described earlier. An outline of this approach is given in the following flow chart:

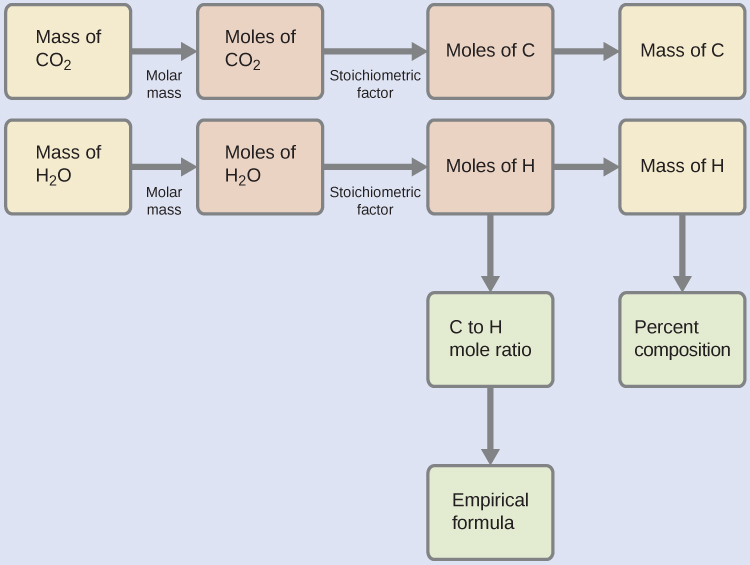
This figure shows two flowcharts. The first row is a single flow chart. In this row, a rectangle at the left is shaded yellow and is labeled, “Mass of C O subscript 2.” This rectangle is followed by an arrow pointing right to a second rectangle. The arrow is labeled, “Molar mass.” The second rectangle is shaded pink and is labeled, “Moles of C O subscript 2.” This rectangle is followed by an arrow pointing right to a third rectangle. The arrow is labeled, “Stoichiometric factor.” The third rectangle is shaded pink and is labeled, “Moles of C.” This rectangle is followed by an arrow labeled “Molar mass” which points right to a fourth rectangle. The fourth rectangle is shaded yellow and is labeled “Mass of C.” Below, is a second flowchart. It begins with a yellow shaded rectangle on the left which is labeled, “Mass of H subscript 2 O.” This rectangle is followed by an arrow labeled, “Molar mass,” which points right to a second rectangle. The second rectangle is shaded pink and is labeled, “Moles of H subscript 2 O.” This rectangle is followed by an arrow pointing right to a third rectangle. The arrow is labeled, “Stoichiometric factor.” The third rectangle is shaded pink and is labeled “Moles of H.” This rectangle is followed to the right by an arrow labeled, “Molar mass,” which points to a fourth rectangle. The fourth rectangle is shaded yellow and is labeled “Mass of H.” An arrow labeled, “Sample mass” points down beneath this rectangle to a green shaded rectangle. This rectangle is labeled, “Percent composition.” An arrow extends beneath the pink rectangle labeled, “Moles of H,” to a green shaded rectangle labeled, “C to H mole ratio.” Beneath this rectangle, an arrow extends to a second green shaded rectangle which is labeled, “Empirical formula.”

mol C  =  0.00394 g CO2 × [latex]\frac{1 \;\text{mol CO}_2}{44.01 \;\text{g/mol}}[/latex] × [latex]\frac{1 \;\text{mol C}}{1 \;\text{mol CO}_2}[/latex]
=  8.95 × 10-5 mol C
mol H  =  0.00161 g H2O × [latex]\frac{1 \;\text{mol H}_2 \text{O}}{18.02 \;\text{g/mol}}[/latex] × [latex]\frac{2 \;\text{mol H}}{1 \;\text{mol H}_2 \text{O}}[/latex]
=  1.79 × 10-4 mol H

The empirical formula for the compound is then derived by identifying the smallest whole-number multiples for these molar amounts. The H-to-C molar ratio is

[latex]\frac{\text{mol H}}{\text{mol C}}[/latex]  =  [latex]\frac{1.79 \times 10^{-4}\;\text{mol H}}{8.95 \times 10^{-5}\;\text{mol C}}[/latex]  =  [latex]\frac{2 \;\text{mol H}}{1 \;\text{mol C}}[/latex]

and the empirical formula for polyethylene is CH2.

Check Your Learning
A 0.00215-g sample of polystyrene, a polymer composed of carbon and hydrogen, produced 0.00726 g of CO2 and 0.00148 g of H2O in a combustion analysis. What is the empirical formula for polystyrene?

Answer:

CH

Example 5

Combustion Analysis of an Organic Compound Containing Oxygen

Combustion analysis of 23.1 mg of a white powder that contains only the elements C, H, and O yields 33.9 mg of CO2 and 13.9 mg of H2O. Determine the empirical formula of the white compound.

Solution

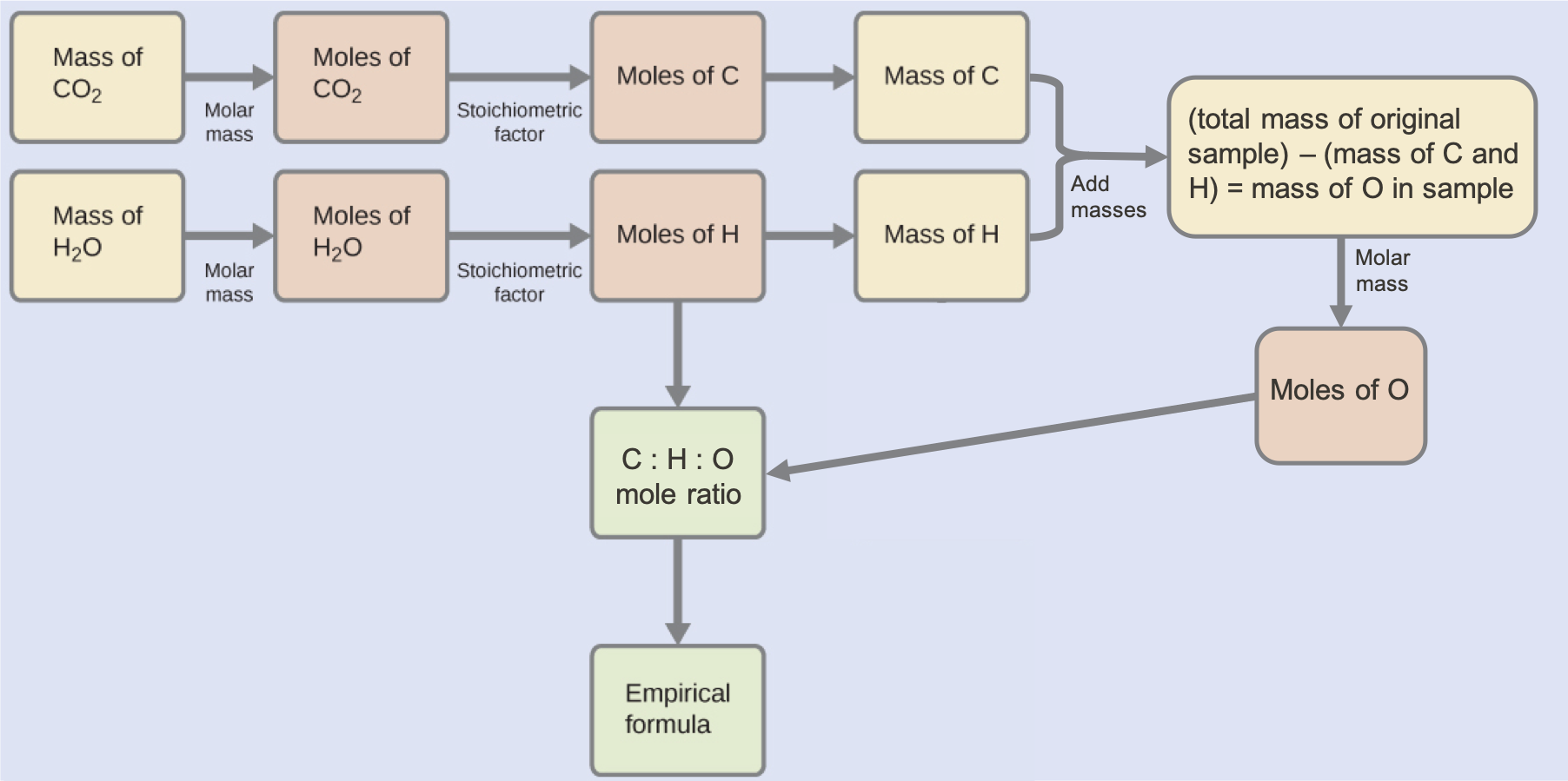
The mass of C and H in the white powder that produced the quantities of CO2 and H2O in the analysis must first be determined. This enables the amount of O in the compound to be calculated by subtraction, as this oxygen does not react in the combustion process.:

mass of C  =  33.9 mg CO2 × [latex]\frac{1 \text{g}}{1000 \text{mg}}[/latex] × [latex]\frac{1 \text{mol CO}_2}{44.01 \text{g}}[/latex] × [latex]\frac{1 \text{mol C}}{1 \text{mol CO}_2}[/latex] × [latex]\frac{12.01 \text{g}}{1 \text{mol C}}[/latex] × [latex]\frac{1000 \text{mg}}{1 \text{g}}[/latex]  =  9.25 mg C

mass of H  =  13.9 mg H2O × [latex]\frac{1 \text{g}}{1000 \text{mg}}[/latex] × [latex]\frac{1 \text{mol H}_2 \text{O}}{18.02 \text{g}}[/latex] × [latex]\frac{2 \text{mol H}}{1 \text{mol H}_2 \text{O}}[/latex] × [latex]\frac{1.008 \text{g}}{1 \text{mol H}}[/latex] × [latex]\frac{1000 \text{mg}}{1 \text{g}}[/latex]  =  1.54 mg H

Because the white powder consists of just three elements and we now know the mass of two of them, the mass of O is the remainder:

mass O  =  23.1 mg – (9.25 mg + 1.54 mg)  =  12.3 mg O

Now the moles of each element can be determined, and the empirical formula determined:

moles C:  9.25 mg C × [latex]\frac{1\;\text{g}}{1000\;\text{mg}}[/latex] × [latex]\frac{1\;\text{mol C}}{12.01\;\text{g}}[/latex]  =  7.70 × 10-4 mol C

moles H:  1.54 mg H × [latex]\frac{1\;\text{g}}{1000\;\text{mg}}[/latex] × [latex]\frac{1\;\text{mol H}}{1.008\;\text{g}}[/latex]  =  1.53 × 10-3 mol H

moles O:  12.3 mg O × [latex]\frac{1\;\text{g}}{1000\;\text{mg}}[/latex] × [latex]\frac{1\;\text{mol C}}{16.00\;\text{g}}[/latex]  =  7.69 × 10-4 mol O

Dividing each of these by the smallest number of moles (7.69 x 10-4 mol) yields the empirical formula: CH2O

This approach is outlined in the following flow chart:

Two flow charts are shown. The first row is a single flow chart. In this row, a rectangle at the left is shaded yellow and is labeled, “Mass of C O subscript 2.” This rectangle is followed by an arrow pointing right to a second rectangle. The arrow is labeled, “Molar mass.” The second rectangle is shaded pink and is labeled, “Moles of C O subscript 2.” This rectangle is followed by an arrow pointing right to a third rectangle. The arrow is labeled, “Stoichiometric factor.” The third rectangle is shaded pink and is labeled, “Moles of C.” This rectangle is followed by an unlabeled arrow pointing right to a fourth rectangle. The fourth rectangle is shaded yellow and labeled, “Mass of C”. Below, is a second flowchart. It begins with a yellow shaded rectangle on the left which is labeled, “Mass of H subscript 2 O.” This rectangle is followed by an arrow labeled, “Molar mass,” which points right to a second rectangle. The second rectangle is shaded pink and is labeled, “Moles of H subscript 2 O.” This rectangle is followed by an arrow pointing right to a third rectangle. The arrow is labeled, “Stoichiometric factor.” The third rectangle is shaded pink and is labeled “Moles of H.” This rectangle is following by an unlabeled arrow pointing right to a fourth rectangle. The fourth rectangle is shaded yellow that is labeled, “Mass of H”. The rectangles labeled “Mass of C” and “Mass of H” have arrows that direct both of these rectangles to a larger rectangle to the right. The arrows are labeled “Add masses” and the larger rectangle is shaded yellow and says, “(total mass of original sample) minus (mass of C and H) equals mass of O in sample”. An arrow points down from this rectangle to another rectangle. The arrow is labeled, “molar mass”. The rectangle below is shaded pink and labeled, “moles of O”. A rectangle shaded green is below the pink rectangle labeled “Moles of H”. This green rectangle has two arrows that enter it, one from the rectangle labeled “Moles of H” and one from the rectangle labeled “Moles of O”. This green rectangle is labeled “C:H:O mole ratio”. An arrow then points down from this rectangle to another green rectangle that says “Empirical formula”.

Check Your Learning

Combustion analysis of 0.112 g of a compound that contains C, H, and O yields 0.0561 g of H2O and 0.205 g of CO2. The hard mass spectrum shows three peaks at 1, 12, and 16 amu, and the soft mass spectrum a single peak at 144 amu. Determine the empirical and actual formula of the compound.

Answer:

The hard mass spectrum indicates the compound consists of the elements C, H, and O.

Empirical Formula C3H4O2, actual Formula C6H8O4

Key Concepts and Summary

The chemical identity of a substance is defined by the types and relative numbers of atoms composing its fundamental entities. To determine an empirical formula, you must find the smallest whole-number ratio of atoms in a molecule. If you begin with the mass of each element in the compound, you must first convert these masses to moles before determining the ratio. A compound’s percent composition provides the mass percentage of each element in the compound, and it is often experimentally determined and used to derive the compound’s empirical formula. The empirical formula mass of a covalent compound may be compared to the compound’s molecular or molar mass to derive a molecular formula.  Combustion analysis can be used to identify an unknown hydrocarbon because the identity of the products are known to be CO2 and H2O.

Key Equations

  • %X  =  [latex]\frac{\text{mass X}}{\text{mass compound}}[/latex] × 100%
  • [latex]\frac{\text{molecular or molar mass (amu or} \;\frac{\text{g}}{\text{mol}})}{\text{empirical formula mass (amu or} \;\frac{\text{g}}{\text{mol}})}[/latex]  =  n formula units/molecule
  • (AxBy)n  =  AnxBny

Glossary

empirical formula mass
sum of average atomic masses for all atoms represented in an empirical formula
combustion analysis
analyical technique used to determine the elemental composition of a compound via the collection and weighing of its gaseous combustion products
percent composition
percentage by mass of the various elements in a compound

Chemistry End of Section Exercises

Empirical Formula

  1. What information do we need to determine the molecular formula of a compound from the empirical formula?
  2. Calculate the following to four significant figures:
    1. the percent composition of ammonia, NH3
    2. the percent composition of photographic “hypo,” Na2S2O3
    3. the percent of calcium ion in Ca3(PO4)2
  3. Determine the percent ammonia, NH3, in Co(NH3)6Cl3, to three significant figures.
  4. Determine the empirical formulas for compounds with the following percent compositions:
    1. 15.8% carbon and 84.2% sulfur
    2. 40.0% carbon, 6.7% hydrogen, and 53.3% oxygen
  5. A compound contains carbon, hydrogen, and chlorine. It has a molar mass of 99 g/mol. Analysis of a sample shows that it contains 24.3% carbon and 4.1% hydrogen. What is its molecular formula?
  6. Determine the empirical and molecular formula for chrysotile asbestos. Chrysotile has the following percent composition: 28.03% Mg, 21.60% Si, 1.16% H, and 49.21% O. The molar mass for chrysotile is 520.8 g/mol.
  7. Polymers are large molecules composed of simple units repeated many times. Thus, they often have relatively simple empirical formulas. Calculate the empirical formulas of the following polymers:
    1. Lucite (Plexiglas); 59.9% C, 8.06% H, 32.0% O
    2. Saran; 24.8% C, 2.0% H, 73.1% Cl
    3. polyethylene; 86% C, 14% H
    4. polystyrene; 92.3% C, 7.7% H
    5. Orlon; 67.9% C, 5.70% H, 26.4% N
  8. A major textile dye manufacturer developed a new yellow dye. The dye has a percent composition of 75.95% C, 17.72% N, and 6.33% H by mass with a molar mass of about 240 g/mol. Determine the molecular formula of the dye.

Combustion Analysis

  1. A 0.025-g sample of a compound composed of boron and hydrogen, with a molecular mass of ~28 amu, burns spontaneously when exposed to air, producing 0.063 g of B2O3. What are the empirical and molecular formulas of the compound? The general reaction is
    BxHy + O2 → B2O3 + H2O (not balanced)
  2. A compound has a molecular mass of about 130 amu, and contains only carbon and hydrogen. A 3.000-mg sample of this compound burns to give 10.3 mg of CO2. Determine its empirical and molecular formulas.
  3. Combustion analysis of 0.112 g of a compound that contains C, H, and O yields 0.0561 g of H2O and 0.205 g of CO2. The hard mass spectrum shows three peaks at 1, 12, and 16 amu, and the soft mass spectrum shows a single peak at 144 amu. Determine the empirical and actual formula of the compound.

Answers to Chemistry End of Section Exercises

  1. You need a given mass and the molar amount of the compound to get the molar mass so it can be compared to the empirical mass
  2. (a) % N = 82.24%, % H = 17.76%; (b) % Na = 29.08%, % S = 40.56%, % O = 30.36%; (c) % Ca2+ = 38.76%
  3. % NH3 = 38.2%
  4. (a) CS2; (b) CH2O
  5. C2H4Cl2
  6. Mg3Si2H3O8 (empirical formula), Mg6Si4H6O16 (molecular formula)
  7. (a) C5H8O2; (b) CHCl; (c) CH2; (d) CH; (e) C3H3N
  8. C15H15N3
  9. The empirical formula is BH3. The molecular formula is B2H6.
  10. Empirical formula: C5H4, molecular formula: C10H8
  11. The hard mass spectrum indicates the compound consists of the elements C, H, and O. Empirical formula: C3H4O2, molecular formula: C6H8O4

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

UW-Madison Chemistry 103/104 Resource Book Copyright © by crlandis is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book