35 Photoelectric Effect (M7Q2)

The Photoelectric Effect

It had been observed since the late 1800s that electrons could be ejected from the clean surface of a metal if irradiated with light. This phenomena is called the photoelectric effect (Figure 1). They observed that electrons could only be ejected when the frequency of the incident light was greater than some threshold frequency, and that the kinetic energy of the ejected electrons increased with increasing frequency of the incident light.  The electrons in the metal had a certain amount of binding energy keeping them bound. Thus, the incident light needed to have more energy than the binding energy in order to free the electrons.

According to classical wave theory, a wave’s energy depends on its intensity (which depends on its amplitude), not its frequency. Therefore, if the photoelectric effect were to be explained in terms of classical wave theory, changing the intensity of the incident light should have determined whether electrons could be ejected, not the frequency. Therefore, a pure classical wave theory explanation of the photoelectric effect was not possible. Scientists did note, however, that the intensity of the light did affect something—the number of electrons ejected in a given time period. In 1905, Albert Einstein was able to resolve the paradox. 

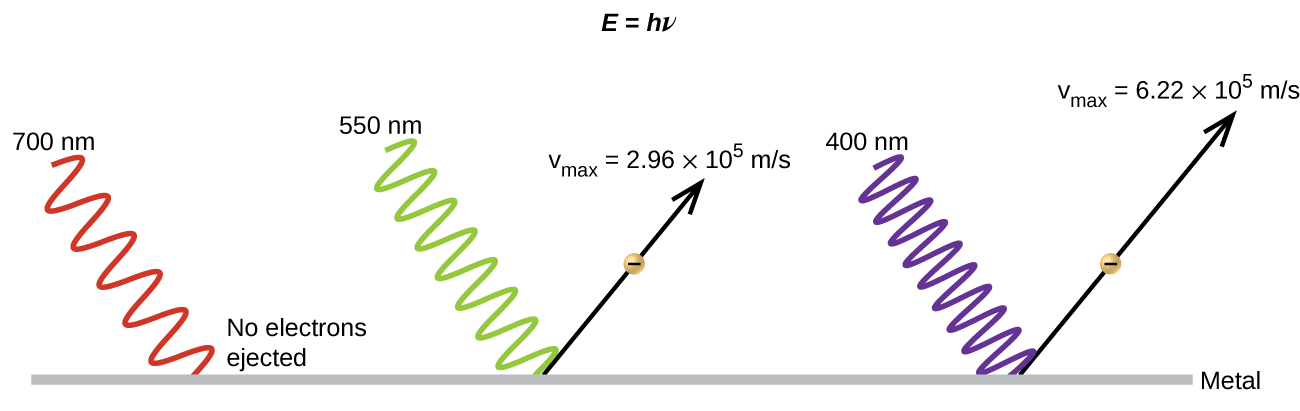
Einstein argued that the light striking the metal surface should not be viewed as a wave (as in the view of classical wave theory), but instead as a stream of particles (later called photons) whose energy depends on their frequency according to the equation, E =  hν (where h is a fundamental physical constant known as Planck’s constant, 6.626 × 10^-34 J·s). Another common form of this equation is in terms of wavelength using c = νλ, E  =  [latex]\frac{hc}{\lambda}[/latex] (the E in these equations is the energy for a single photon). Einstein explained that electrons were ejected when hit by photons having sufficient energy (a frequency greater than the threshold). The greater the frequency of the incident photon (and thus the greater the energy of the photon), the greater the kinetic energy imparted to the escaping electrons. Einstein argued that if we think of light consisting of photons, then the intensity of light depends on the number of photons striking the surface times the energy per photon, as opposed to the amplitude of the incoming wave.This explains why the number of ejected electrons increased with increasing intensity of incident light, since the greater the number of incoming photons, the greater the likelihood that they would collide with some of the electrons.

Einstein postulated that each metal has a particular electrostatic attraction for its electrons that must be overcome before an electron can be emitted from its surface. This value is called the binding energy (E_BE). If photons of light with energy less than E_BE strike a metal surface, no single photon has enough energy to eject an electron, so no electrons are emitted regardless of the intensity of the light. This is an important observation since it showed that the energy of the photons was quantized, or had discrete amounts of energy, and could not be added together to eject a single electron. One photon could eject, at most, one electron. If a photon with energy greater than E_BE strikes the metal, then part of its energy is used to overcome the forces that hold the electron to the metal surface, and the excess energy appears as the kinetic energy (E_KE) of the ejected electron:

E_photon  =  E_BE + E_KE

Recall from physics (and from the previous module) that E_KE = ½ mv², where m in this case is the mass of the electron (9.11 × 10^-31 kg)  and v is the velocity of the electron (in m/s).

Because the photoelectric effect could not be described using wavelike properties, it suggested a particle-like nature of light where the energy of the electromagnetic radiation depends on the frequency (or wavelength) of light, not the intensity of the light. This was the first time that scientists had encountered something that exhibited both wave-like and particle properties. Sometimes it was better to treat electromagnetic radiation as a wave and sometimes as a stream of photons, two seemingly contradictory pictures of reality which independently could not fully explain the phenomena of light, but together they could. It took many years for the scientific community to accept the wave/particle nature of light, and even today the full meaning of wave/particle duality is still debated.

Blackbody Radiation and the Ultraviolet Catastrophe

You have just seen that electromagnetic radiation demonstrates properties of particles called photons. The concept of photons was originally described by Einstein for the purposes of the photoelectric effect, however, several years earlier (1900) Max Planck, in an effort to describe blackbody radiation, developed mathematical expressions that, in hindsight, suggested the particle properties of light to Einstein.  His discovery resolved the apparent contradiction of blackbody radiation, the first phenomenon which caused scientists to recognize the fundamental limitations of classical physics.

A blackbody is a convenient, ideal emitter that approximates the behavior of many materials when heated. A blackbody is “ideal” in the same sense that an ideal gas is a convenient, simple representation of real gases that works well, provided that the pressure is not too high nor the temperature too low. A good approximation of a blackbody that can be used to observe blackbody radiation is a metal oven that can be heated to very high temperatures. The oven has a small hole allowing for the light being emitted within the oven to be observed with a spectrometer, an instrument that can measure the wavelengths and intensities of light. Figure 2 shows the resulting curves for some representative temperatures. Each distribution depends only on a single parameter: the temperature. The wavelength at which the maximum intensity is observed in the blackbody curves, λ_max, shift to shorter wavelengths as the temperature increases, reflecting the observation that metals being heated to high temperatures begin to glow a darker red that becomes brighter as the temperature increases, eventually becoming white hot at very high temperatures as the intensities of all of the visible wavelengths become appreciable.

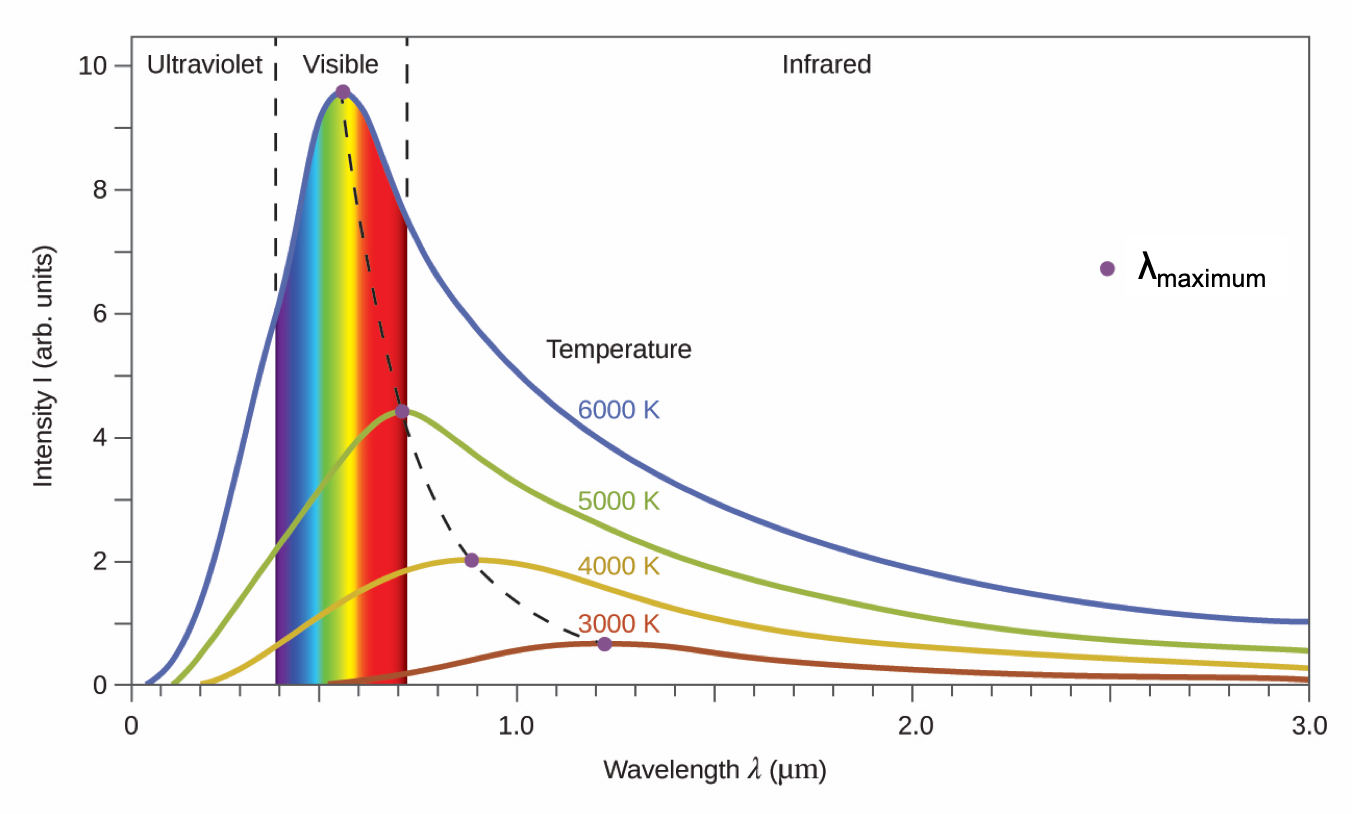
Physicists derived mathematical expressions for the blackbody curves using well-accepted concepts from the theories of classical mechanics and classical electromagnetism. The theoretical expressions as functions of temperature fit the observed experimental blackbody curves well at longer wavelengths, but showed significant discrepancies at shorter wavelengths. Not only did the theoretical curves not show a peak, they absurdly showed the intensity becoming infinitely large as the wavelength became smaller and approached the UV region. This became known as the “ultraviolet catastrophe” because no one could find any problems with the theoretical treatment that could lead to such unrealistic short-wavelength behavior.

Finally, Max Planck derived a theoretical expression for blackbody radiation that fit the experimental observations exactly (within experimental error). Planck developed his theoretical treatment by extending the earlier work that had been based on the premise that the atoms composing the oven vibrated at increasing frequencies (or decreasing wavelengths) as the temperature increased, with these vibrations being the source of the emitted electromagnetic radiation. But where the earlier treatments had allowed the vibrating atoms to have any energy values obtained from a continuous set of energies (perfectly reasonable, according to classical physics), Planck found that by restricting the vibrational energies to discrete values for each frequency, he could derive an expression for blackbody radiation that correctly had the intensity dropping rapidly for the short wavelengths in the UV region: E  =  hν. We used this equation above to calculate the energy of a photon, but it originated with Planck in his description of blackbody radiation. The quantity h is a constant now known as Planck’s constant, in his honor. Although Planck was pleased he had resolved the blackbody radiation paradox, he was disturbed that to do so, he needed to assume the vibrating atoms required quantized energies, which he was unable to explain. The value of Planck’s constant is very small, 6.626 × 10⁻³⁴ Joule seconds (J·s), which helps explain why energy quantization had not been observed previously in macroscopic phenomena.