60 Types of Unit Cells: Primitive Cubic Cell (M11Q4)

Introduction

In this section, we take a closer look at crystalline solids by looking at elemental metals. The structure of these solids can be described by their unit cells. We will look at the most basic unit cell here — the primitive cubic cell.

Learning Objectives for Types of Unit Cells: Primitive Cubic Cell

 

| Key Concepts and Summary | Glossary | End of Section Exercises |

Over 90% of naturally occurring and man-made solids are crystalline. Most solids form with a regular arrangement of their particles because the overall attractive interactions between particles are maximized, and the total intermolecular energy is minimized, when the particles pack in the most efficient manner. The regular arrangement at an atomic level is often reflected at a macroscopic level.

The Structures of Metals

We will begin our discussion of crystalline solids by considering elemental metals, which are relatively simple because each contains only one type of atom. A pure metal is a crystalline solid with metal atoms packed closely together in a repeating pattern. Some of the properties of metals in general, such as their malleability and ductility, are largely due to having identical atoms arranged in a regular pattern. The different properties of one metal compared to another partially depend on the sizes of their atoms and the specifics of their spatial arrangements.

Unit Cells of Metals

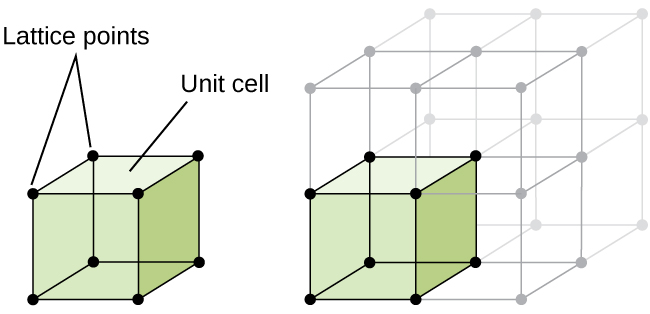
The structure of a crystalline solid, whether a metal or not, is best described by considering its simplest repeating unit, which is referred to as its unit cell. The unit cell consists of lattice points that represent the locations of atoms or ions. The entire structure then consists of this unit cell repeating in three dimensions, as illustrated in Figure 1.

A diagram of two images is shown. In the first image, a cube with a sphere at each corner is shown. The cube is labeled “Unit cell” and the spheres at the corners are labeled “Lattice points.” The second image shows the same cube, but this time it is one cube amongst eight that make up a larger cube. The original cube is shaded a color while the other cubes are not.
Figure 1. A unit cell shows the locations of lattice points repeating in all directions.

Primitive Cubic (PC) Cell

Let us begin our investigation of crystal lattice structure and unit cells with the most straightforward structure and the most basic unit cell. To visualize this, imagine taking a large number of identical spheres, such as tennis balls, and arranging them uniformly in a container. The simplest way to do this would be to make layers in which the spheres in one layer are directly above those in the layer below, as illustrated in Figure 2. This arrangement is called primitive cubic structure, and the unit cell is called the primitive cubic unit cell or simple cubic unit cell.

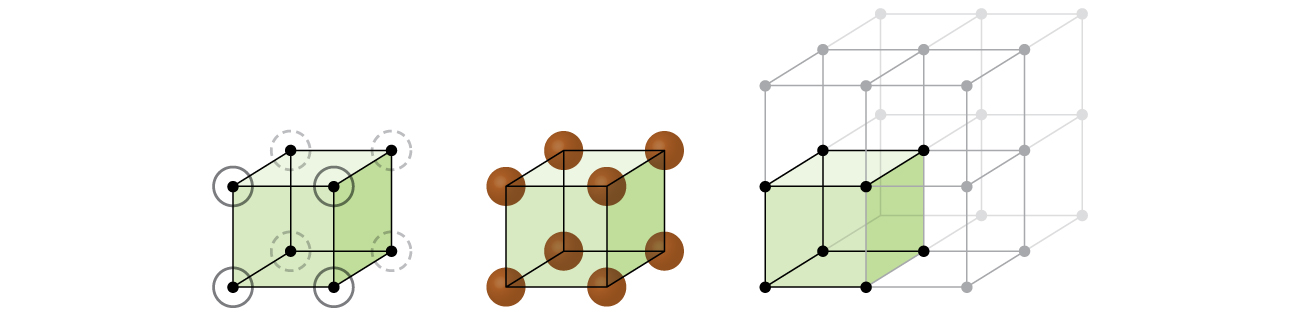
A diagram of three images is shown. In the first image, a cube with a sphere at each corner is shown. The spheres at the corners are circled. The second image shows the same cube, but this time the spheres at the corners are larger and shaded in. In the third image, the cube is one cube amongst eight that make up a larger cube. The original cube is shaded a color while the other cubes are not.
Figure 2. When metal atoms are arranged with spheres in one layer directly above or below spheres in another layer, the lattice structure is called primitive cubic. Note that the spheres are in contact.

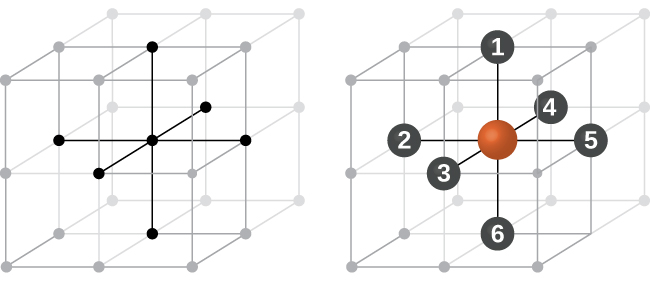
In a primitive cubic structure, the spheres are not packed as closely as they could be, and they only “fill” about 52% of the volume of the container. This is a relatively inefficient arrangement, and only one metal (polonium, Po) crystallizes in a simple cubic structure. As shown in Figure 3, a solid with this type of arrangement consists of planes (or layers) in which each atom contacts only the four nearest neighbors in its layer; one atom directly above it in the layer above; and one atom directly below it in the layer below. The number of other particles that each particle in a crystalline solid contacts is known as its coordination number. For a polonium atom in a primitive cubic array, the coordination number is six.

A diagram of two images is shown. In the first image, eight stacked cubes that make up one large cube are shown. Three lines that run from top to bottom, front to back and sided to side in the middle of the structure are shaded darker than the rest of the lines. The second image shows the same set of cubes, but this time spheres at the end of each line are numbered; the horizontal line that goes left to right is labeled with a “2” and a “5,” the vertical line is labeled with a “1” and a “6” and the line that goes horizontally front to back is labeled with a “3” and a “4.”
Figure 3. An atom in a primitive cubic lattice structure contacts six other atoms, so it has a coordination number of six.

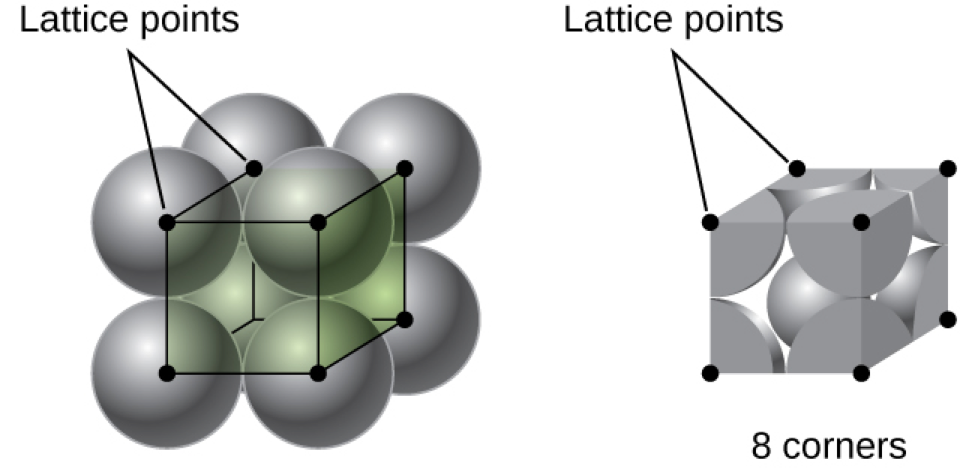
In a primitive cubic lattice, the unit cell that repeats in all directions is a cube defined by the centers of eight atoms, as shown in Figure 4. Atoms at adjacent corners of this unit cell contact each other, so the edge length of this cell is equal to two atomic radii, or one atomic diameter. A cubic unit cell contains only the parts of these atoms that are within it. Since an atom at a corner of a primitive cubic unit cell is contained by a total of eight unit cells, only one-eighth of that atom is within a specific unit cell. And since each primitive cubic unit cell has one atom at each of its eight “corners,” there is [latex]8\;\times\;\frac{1}{8} = 1[/latex] atom within one simple cubic unit cell.

 

A diagram of two images is shown. In the first image, eight spheres are stacked together to form a cube and dots at the center of each sphere are connected to form a cube shape. The dots are labeled “Lattice points”. The second image shows the portion of each sphere that lie inside the cube. The corners of the cube are shown with small circles labeled “Lattice points” and the phrase “8 corners” is written below the image.
Figure 4. A primitive cubic lattice unit cell contains one-eighth of an atom at each of its eight corners, so it contains one atom total.

Example 1

Calculation of Atomic Radius and Density for Metals, Part 1
The edge length of the unit cell of alpha polonium is 336 pm.

(a) Determine the radius of a polonium atom.

(b) Determine the density of alpha polonium.

Solution
Alpha polonium crystallizes in a simple cubic unit cell:

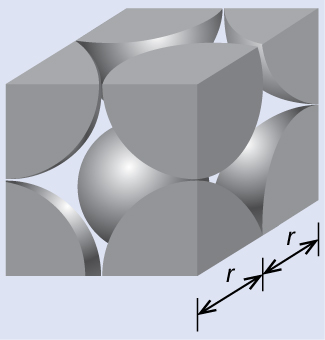
A diagram shows a cube with a one eighth portion of eight spheres inside the cube, one section in each corner. Along the bottom right side of the cube are two double ended arrows that each stretch along half of the total distance across the cube. Each arrow is labeled “r.”

(a) Two adjacent Po atoms contact each other, so the edge length of this cell is equal to two Po atomic radii: l = 2r. Therefore, the radius of Po is r = [latex]\frac{\text{l}}{2}[/latex] = [latex]\frac{336\;\text{pm}}{2}[/latex] = 168 pm.

(b) Density is given by density = [latex]\frac{\text{mass}}{\text{volume}}[/latex]. The density of polonium can be found by determining the density of its unit cell (the mass contained within a unit cell divided by the volume of the unit cell). Since a Po unit cell contains one-eighth of a Po atom at each of its eight corners, a unit cell contains one Po atom.

The mass of a Po unit cell can be found by:

1 Po unit cell ×  [latex]\frac{1\;\text{Po atom}}{1\;\text{Po unit cell}}[/latex]  ×  [latex]\frac{1\;\text{mol Po}}{6.022\;\times\;10^{23}\;\text{Po atoms}}[/latex] ×  [latex]\frac{208.998\;\text{g}}{1\;\text{mol Po}}[/latex] = 3.47 ×  10-22 g

The volume of a Po unit cell can be found by:

V = l3 = (336 ×  10-10 cm)3 = 3.79 ×  10-23 cm3

(Note that the edge length was converted from pm to cm to get the usual volume units for density.)

Therefore, the density of Po = [latex]\frac{3.471\;\times\;10^{-22}\;\text{g}}{3.79\;\times\;10^{-23}\;\text{cm}^3}[/latex] = 9.16 g/cm3

Check Your Learning
The edge length of the unit cell for nickel is 0.3524 nm. The density of Ni is 8.90 g/cm3. Does nickel crystallize in a simple cubic structure? Explain.

Answer:

No. If Ni was simple cubic, its density would be given by:

1 Ni atom ×  [latex]\frac{1\;\text{mol Ni}}{6.022\;\times\;10^{23}\;\text{Ni atoms}}[/latex] ×  [latex]\frac{58.693\;\text{g}}{1\;\text{mol Ni}}[/latex] = 9.746 ×  10-23 g

V = l3 = (3.524 ×  10-8 cm)3 = 4.376 ×  10-23 cm3

Then the density of Ni would be = [latex]\frac{9.746\;\times\;10^{-23}\;\text{g}}{4.376\;\times\;10^{-23}\;\text{cm}^3}[/latex] = 2.23 g/cm3

Since the actual density of Ni is not close to this, Ni does not form a simple cubic structure.

Key Concepts and Summary

A unit cell is the simplest repeating unit of a crystalline solid. The simplest unit cell is the primitive cubic unit cell in which there are atoms at each of the 8 corners of a cube. In this type of unit cell: the coordination number is 6, there is 1 atom per cell, and the length of the edge of a cell is equal to 2r.

Glossary

coordination number
number of atoms closest to any given atom in a crystal or to the central metal atom in a complex
primitive cubic unit cell
(also, simple cubic unit cell) unit cell in the simple cubic structure
primitive cubic structure
crystalline structure with a cubic unit cell with lattice points only at the corners
unit cell
smallest portion of a space lattice that is repeated in three dimensions to form the entire lattice

Chemistry End of Section Exercises

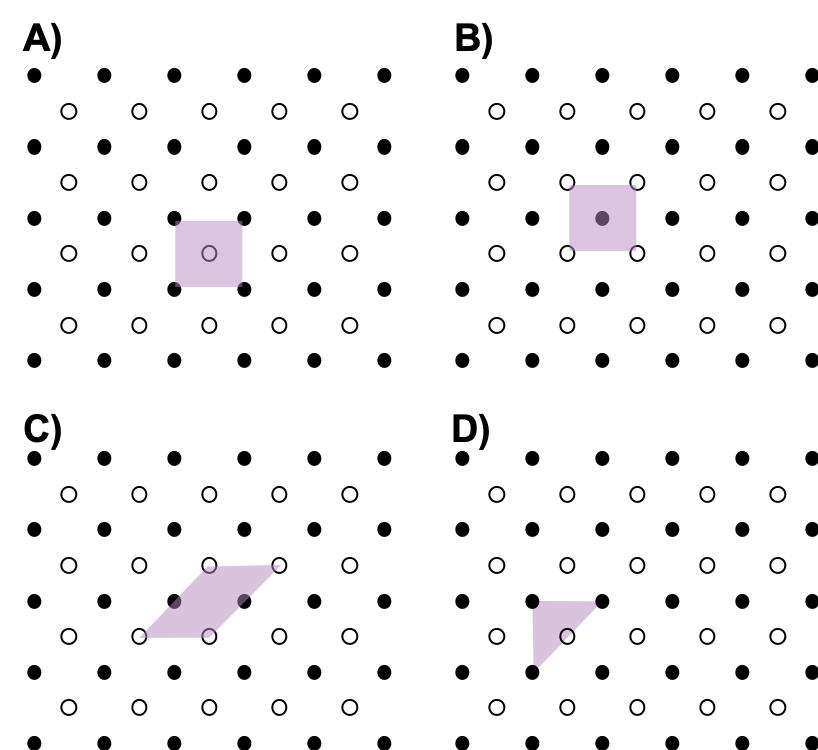
  1. Which of the following is not a unit cell for the following array? Explain.
    There are 4 options shown, labeled “A” through “D”. The grid in each option is the same. There is a row of 6 black circles. Below this row is a row of 5 white circles. The white circles are situated so that they are offset with the black circles above. These two rows alternate so that the third row has black circles and is directly beneath the first row of black circles, and the fourth row has white circles and is directly beneath the second row of white circles. Option “A” shows purple boxes drawn that connect four black circles in a square, with one white circle contained inside the square. Option “B” shows purple boxes drawn that connect four white circles in a square, with one black circle inside the square. Option “C” shows parallelograms with two adjacent white circles connected horizontally, then each circle is connected to a black circle in the row beneath and to the left. Then the black circles are connected to two white circles in the row beneath and to the left. The white circles are then connected together so that the final shape is a slanted rectangle. Option “D” shows triangles. The first black circle is connected to a black circle to its right (circle 2) and a black circle directly beneath it (circle 3). Circles 2 and 3 are then connected, and the line that connects them bisects a white circle.
  2. Show that only about 52% of the volume of a primitive cubic unit cells is occupied. The volume of a sphere is Vsphere = [latex]\frac{4}{3}[/latex]πr3.

Answers to Chemistry End of Section Exercises

  1. Usually the smallest unit cell that completely describes the order is chosen. The only requirement for a valid unit cell is that repeating it in space must produce the regular lattice. Thus the unit cell in (D) is not a valid choice because repeating it in space does not produce the desired lattice (there are triangular holes).
  2. Let length of cube = a = 2r (r = radius of sphere). Volume of the unit cell (Vcell) = a3 = 8r3. Therefore, Vsphere/Vcell = (4/3)πr3/8r3 = π/6 = 0.52, or 52%

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

UW-Madison Chemistry 103/104 Resource Book Copyright © by crlandis is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book