Unit Three

Day 22: Elementary Reactions

D22.1 Elementary Reactions

A balanced equation for a chemical reaction indicates which substances react, which substances are produced when the reaction is over, and how the amounts of reactants and products are related. But it does not necessarily show what happens on the atomic scale as the reaction takes place. Although it is not obvious on the laboratory scale, most chemical reactions occur as a series of atomic-scale steps; that is, as a sequence of simpler reactions, each of which often involving collisions between molecules. The step-by-step sequence of simple reactions by which an overall reaction occurs is called a reaction mechanism.

For example, ozone in the stratosphere protects Earth’s surface from harmful ultraviolet radiation. Ultraviolet photons cause ozone molecules to decompose to oxygen molecules. The overall reaction equation is:

2 O3(g) [latex]\overset{h\nu}{\rightarrow}[/latex] 3 O2(g)

However, at the atomic scale this reaction does not involve collision and reaction between two O3 molecules. Rather, there are two steps that occur one after the other:

step 1: O3(g) [latex]\overset{h\nu}{\rightarrow}[/latex] O2(g) + O(g)
step 2: O(g) + O3(g) ⟶ 2 O2(g)
overall: 2 O3(g) ⟶ 3 O2(g)

In step 1, upon absorption of an UV photon, a bond breaks in an O3 molecule producing an O2 molecule and an O atom:

In step 2, the O atom formed in step 1 reacts with a second O3 molecule, producing two O2 molecules:

The overall reaction is the sum of the two steps. Write reactants from all steps to the left of a reaction arrow; write products from all steps to the right of the arrow; then cancel formulas that appear on both sides of the arrow. This gives

O3(g) + O(g) + O3(g) ⟶ O2(g) + O(g) + 2O2(g)

which is the overall reaction equation given above: 2 O3(g) ⟶ 3 O2(g). An atom or molecule that is a product in an earlier step and reacts away in a later step of a reaction mechanism is called a reaction intermediate.

Each step in a reaction mechanism is called an elementary reaction, which is a chemical reaction that has only a single transition state. An elementary reaction shows which atomic-scale particles collide, break apart, or rearrange their structures to form reaction products and/or intermediates.

The equation for an elementary reaction specifies exactly which atoms or molecules are involved in that reaction. For example, step 2 in the ozone decomposition reaction mechanism above states that one O atom reacts with one O3 molecule and two O2 molecules are formed. That is, for this elementary reaction to occur, one O atom must collide with (come very close to) one O3 molecule.

In contrast, the overall reaction equation does not necessarily specify which atoms or molecules collide and react. Even though the overall ozone reaction is 2 O3(g) ⟶ 3 O2(g), two O3 molecules do not have to collide for products to appear.

Because each elementary reaction has a single transition state, in an overall reaction that consists of several sequential elementary reaction steps there is a series of transition states, one for each step in the mechanism. For example, Figure 1 shows the overall reaction energy diagram for the ozone decomposition reaction.

Figure 1. Reaction energy diagram for the overall 2 O3(g) → 3 O2(g) reaction. This reaction proceeds via a mechanism consisting of two elementary reaction steps. Click on each + sign to identify each chemical species in the diagram.

Note that although one of the O3 molecules does not react until step 2, you still need to include it as a reactant in the reaction energy diagram. In other words, in a reaction energy diagram, all the atoms and molecules that are involved in the reaction are accounted for from the very beginning to the end. Hence, step 1 could be written 2 O3(g) ⟶ O2(g) + O(g) + O3(g), to emphasize that one O3 molecule has not yet reacted, and step 2 becomes O2(g) + O(g) + O3(g) ⟶ 3 O2(g). This is because there is a significant quantity of energy associated with each atom or molecule; to omit one, or suddenly add one in the middle of the diagram would change the energy (y-axis) a lot.

Exercise 1: Reaction Mechanism

D22.2 Unimolecular Elementary Reactions

A unimolecular elementary reaction involves the rearrangement of a single reactant molecule to produce one or more product molecules. The isomerization of cis-1,2-difluoroethene (Section 21.2), step 1 in the mechanism for ozone decomposition given above, and many radioactive decay reactions (Day 20), are all examples of unimolecular elementary reactions.

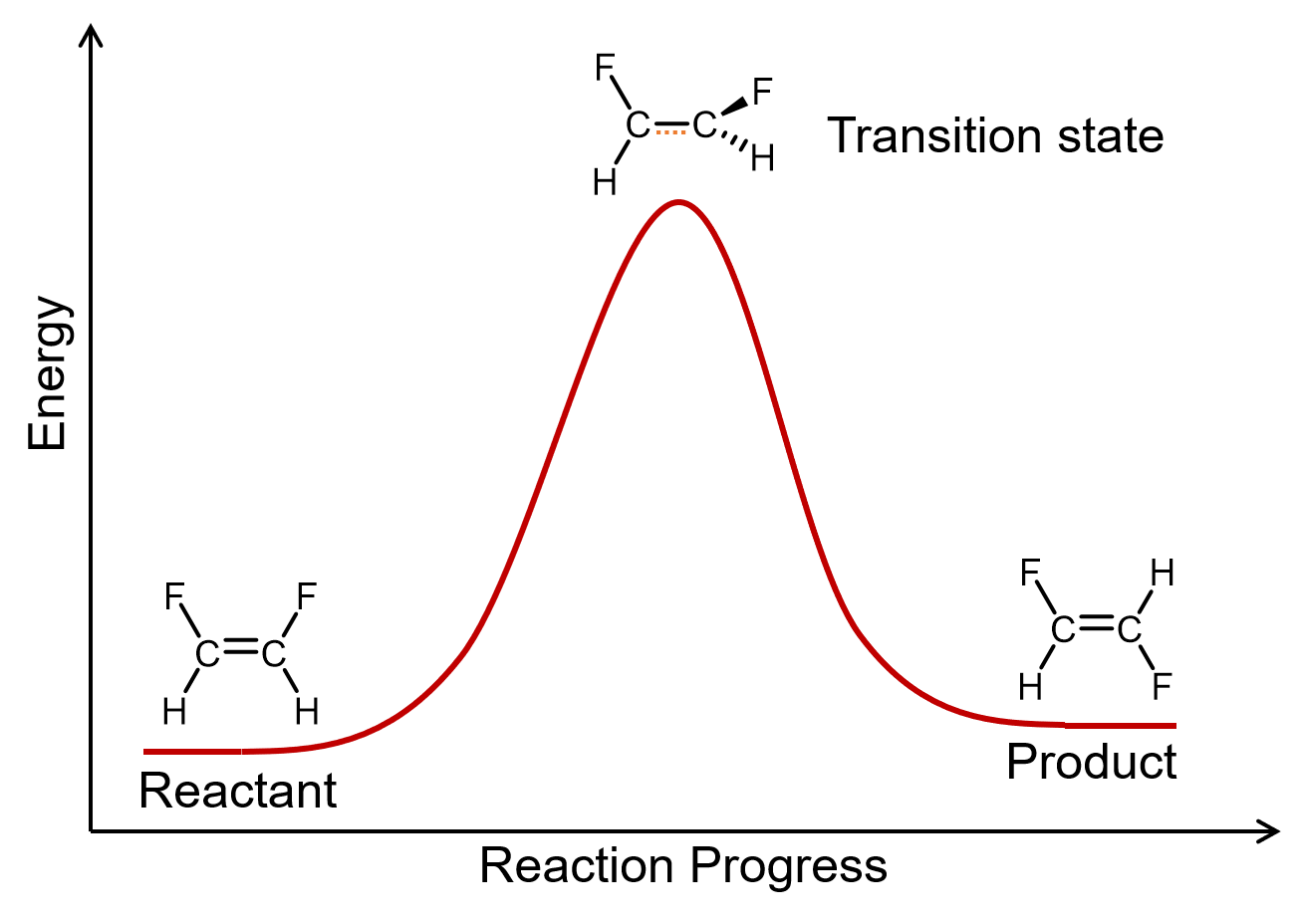
Figure 2. Reaction energy diagram of the cis-trans isomerization of cis-1,2-difluoroethene, an example of a unimolecular elementary reaction. In the transition state, the bond that is breaking (π bond) is shown as a dash and it is highlighted in orange.

A general equation for a unimolecular elementary reaction is:

A → products

Suppose that a 1.0-L flask contains 0.0010 mol of reactant A. The concentration of A is 0.0010 mol/1.0 L = 0.0010 M. At any given temperature a tiny fraction of the A molecules has enough energy to overcome the activation-energy barrier and react. If we add another 0.0010 mol A to the flask, the number of A molecules doubles and the concentration of A doubles to 0.0020 M. If the temperature remains the same, the fraction of molecules that has enough energy to react remains the same, but now there are twice as many molecules so the number of molecules reacting (and the rate of reaction) doubles; that is, the rate of reaction is directly proportional to the concentration of A. Thus, the rate equation for a unimolecular reaction is:

rate = k[A]

If a reaction is known to be a unimolecular elementary reaction, its reaction rate is directly proportional to the concentration of the reactant and the reaction is overall first-order. We see here that because an elementary reaction describes exactly the reaction that is occurring, it is possible to determine the order of an elementary reaction solely by looking at the equation. This is true for all elementary reactions.

Exercise 2: Unimolecular Reactions

D22.3 Bimolecular Elementary Reactions

The collision and reaction of two molecules or atoms in an elementary reaction is a bimolecular elementary reaction. There are two general types of bimolecular elementary reactions. In one type, the two reactants are different:

A + B → products

The rate law for such a reaction is first-order in [A] and [B]:

rate = k[A][B]

In the other type of bimolecular elementary reaction, the two reactants are the same:

A + A → products          or          2 A → products

The rate law for such a reaction is second-order in [A]:

rate = k[A]2

If a reaction is known to be a bimolecular elementary reaction, then its rate law can be derived by considering how concentration of each reactant affects the number of collisions. This is shown in Figure 3. Assuming that the fraction of collisions that results in reaction is the same in all three cases, the rate of reaction doubles when the number (and concentration) of each type of molecule doubles. The rate law derived from number of collisions agrees with the rate law derived from the reaction equation. A bimolecular reaction is overall second-order.

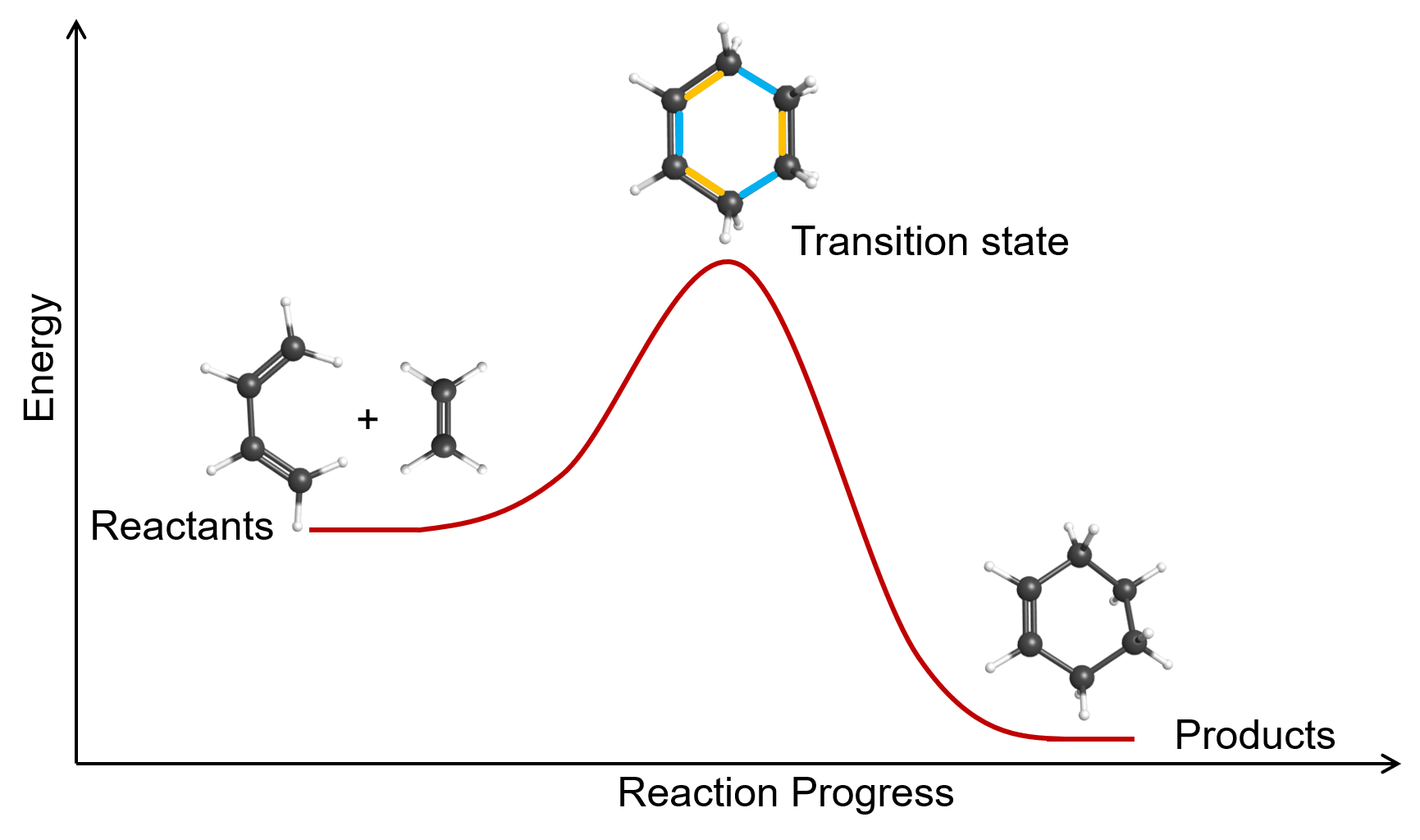
Figure 3. The effect of concentration on the frequency of collisions for a bimolecular reaction. (a) A single black molecule moving among 50 white molecules traces the path shown and collides with 5 white molecules in 1 s. Each white molecule that has been struck by a moving black molecule is shown in color. (b) If the number of white molecules is doubled, the frequency of collisions rises to 10 per second. (c) Two black molecules moving among 50 white ones produce 10 collisions per second. The number of collisions can thus be seen to be proportional to both the concentration of white molecules and the concentration of black molecules.

Some chemical reactions have mechanisms that consist of a single bimolecular elementary reaction. An example is the gas-phase reaction of 1,3-butadiene with ethene to form cyclohexene, shown in Figure 4.

C4H6(g) + C2H4(g) → C6H10(g)               rate = k[C4H6][C2H4]
Figure 4. The probable mechanism for the reaction of 1,3-butadiene with ethene to produce cyclohexene. In the transition state, bonds that are breaking (three π bonds) are shown in orange and bonds that are forming (one π bond and two σ bonds) are shown in cyan.

Another example of a bimolecular elementary reaction is step 2 in the ozone decomposition mechanism given earlier:

O(g) + O3(g) → 2O2(g)               rate = k[O][O3]

Exercise 3: Bimolecular Reactions

Exercise 4: Steric Factor

D22.4 Trimolecular Elementary Reactions

An trimolecular (or termolecular) elementary reaction involves the simultaneous collision of three atoms or molecules. Trimolecular elementary reactions are very unlikely, because the probability of three particles colliding simultaneously is less than 0.1% of the probability of two particles colliding. When a reaction involves three reactant molecules, it is much more likely for it to proceed via a multi-step mechanism involving unimolecular and/or bimolecular elementary reaction steps.

While there are rare examples of trimolecular elementary reaction occurring under certain conditions, in general, the individual steps in reaction mechanisms for gas-phase reactions are restricted to unimolecular and bimolecular reactions.

Exercise 5: Rate Law for an Elementary Reaction

Day 22 Pre-class Podia Problem: Activated Complex (Transition State)

Consider the gas-phase decomposition of cyclobutane, C4H8, to ethylene, C2H4, which occurs via a unimolecular elementary reaction:

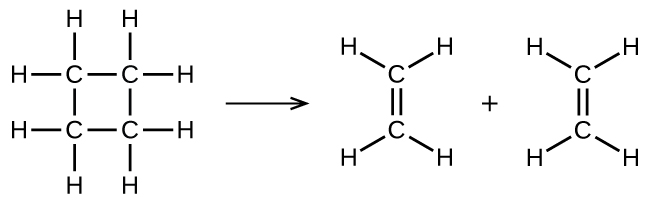
In this figure, structural formulas are used to illustrate a chemical reaction. On the left, a structural formula for cyclobutane is shown. This structure is composed of 4 C atoms connected with single bonds in a square shape. Each C atom is bonded to two other C atoms in the structure, leaving two bonds for H atoms pointing outward above, below, left, and right. An arrow points right to two identical ethane molecules with a plus symbol between them. Each of these molecules contains two C atoms connected with a double bond oriented vertically between them. The C atom at the top of these molecules has H atoms bonded above to the right and left. Similarly, the lower C atom has two H atoms bonded below to the right and left.

1. Write the rate law for this reaction. Express the rate of reaction in terms of concentration. (Don’t just write “rate =”, use Δ[A]/Δt.)

2. Describe in words which bonds must break and which bonds must form when this reaction occurs.

3. Based on your description in part 2, suggest a structure for the activated complex (transition state) for this reaction. Use dotted lines to indicate existing bonds that are partially broken or new bonds that are partially formed.

4. At the temperature of the kinetic study the reaction energy change, ΔrE = – 300 kJ/mol. The activation energy, Ea = 261 kJ/mol. Use this information to draw a reaction energy diagram. Make the vertical axis scale as accurate as possible. Draw the structures of the reactant, the transition state, and the product molecules at appropriate positions on the diagram.

Two days before the next whole-class session, this Podia question will become live on Podia, where you can submit your answer.

Comments. If you found any inconsistencies, errors, or other things you would like to report about this module, please use this link to report them. A similar link will be included in each day’s material. We appreciate your comments.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chemistry 109, Fall 2020 Copyright © by John Moore; Jia Zhou; and Etienne Garand is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.