D24.1 Enzymes

Millions of chemical reactions occur within each of our cells every minute. Without catalysts, many of these reactions proceed at an extremely slow rate. For example, the dissociation of carbonic acid that takes place in the lungs:

only proceeds at a rate of ~10^-7 M/s at room temperature. However, CO₂ needs to be produced in our body at a much higher rate than this. While it’s theoretically possible to accelerate the reaction by raising the temperature, unfortunately, most life is only compatible with a limited temperature range.

Biological catalysts, known as enzymes, are crucial for life as they can accelerate reactions by factors of 10⁶-10²⁰. For example, the enzyme carbonic anhydrase accelerates the above reaction at room temperature by more than a million times the rate of the uncatalyzed reaction.

Like all catalysts, enzymes act by combining with reactant(s) and thereby forming lower energy transition states. In an enzyme-catalyzed reaction, the reactant(s) with which the enzyme combines is called the substrate(s). Unlike chemical catalysts, an enzyme’s interactions with substrate molecules are often partly or entirely noncovalent; that is, the interactions involve hydrogen bonding, ionic attractions, or dipole-dipole attractions.

In addition, enzyme-catalyzed reactions are highly specific to a particular substrate or a particular category of substrate molecules. Enzymes are said to “recognize” the substrate, or class of substrates, for which the enzyme serves as a catalyst. Enzyme interactions with substrates are sometimes so specific that an enzyme does not recognize a molecule that differs from its preferred substrate by as little as a single methyl (-CH₃) group, and many enzymes will recognize one enantiomer but not its mirror image.

How do enzymes accelerate chemical reactions and achieve their specificity? The answer to both questions lies in how enzymes interact with their substrates. Typically an enzyme is a protein molecule—a macromolecule. Usually only part of the large enzyme molecule interacts with a substrate. The part of an enzyme molecule that interacts with a substrate is called the active site.

In 1890, the chemist Emil Fischer proposed that the substrate fits into the enzyme’s active site as a key fits into a lock. The key (substrate) has a specific molecular shape (arrangement of functional groups and other atoms) that allows it, and no other key, to fit into the lock (the enzyme).

In 1958, Daniel E. Koshland Jr. modified this lock-and-key model by proposing that binding of the substrate to the enzyme alters the configuration of both, providing a better fit. This induced-fit model explains both the large increase in reaction rates and the specificity of enzyme-catalyzed reactions:

• As the substrate interacts with the enzyme, the substrate is distorted (atoms are shifted, bonds are stretched, and reactive groups are brought close together) to a structure closer to the transition state of the reaction. This lowers the energy of the transition state, accelerating the reaction.
• Only molecules with the correct functional groups in the correct configurations are able to be induced to fit the active site of the enzyme.

For many years, it was believed that the only enzymes were proteins. Recently, however, several RNA enzymes have been discovered. These enzymes are called ribozymes and exhibit all the same features as protein enzymes (Figure 2).

D24.2 Enzyme Kinetics: Michaelis-Menten Mechanism

The Michaelis-Menten mechanism is a two-step reaction mechanism that applies to many enzyme-catalyzed reactions. An enzyme (E) binds with a substrate (S) to form an enzyme-substrate complex (ES), which then separates to give the product (P) and regenerates the enzyme. The overall reaction is:

with the simple two-step mechanism:

The second step is rate determining. Enzyme kinetics studies are typically carried out by measuring the reaction rate as a function of the concentration of substrate and the concentration of enzyme. The rate of the catalyzed reaction can be measured by observing the rate of the production of the product:

but ES is a reactive intermediate whose concentration is not easily determined. We need to express the reaction rate in terms of concentrations that are easily measured. This can be done by assuming that, once the reactive intermediate, ES, forms, its concentration remains approximately constant throughout the rest of the reaction; this is called the steady-state approximation. It differs from the equilibrium approximation we discussed in Section D23.3 in that it is not necessary to assume step 1 has reached equilibrium. The steady-state approximation is reasonable, because once [ES] builds up enough, the reactions that consume ES become faster and prevent the concentration from increasing further.

When the concentration of the enzyme-substrate complex reaches a steady state:

The ES complex is formed by the forward reaction in step 1, and is reacted away in the reverse reaction of step 1 and forward reaction of step 2. Summing the rates of these reactions:

Rearranging the equation to solve for [ES] gives:

or:

where K_M is the Michaelis constant:

It is difficult to know the exact concentration of the free enzyme ([E]) at any given moment. However, we do know the total concentration of enzyme, [E]_total (the enzyme must be either in its unreacted form (E) or combined with substrate (ES)):

Substituting into the above equation gives:

Rearranging the variables gives:

Substituting the expression for [ES] into the expression for the reaction rate in terms of [ES} gives

or

where V_max = k₂[E]_total is the maximum rate the reaction can achieve. There are two limiting cases for this equation, depending on the relative sizes of [S] and K_M.

If there is a lot of substrate, [S] ≫ K_M, and therefore [S] + K_M ≈ [S]. In this case the Michaelis-Menten equation becomes

[latex]\text{rate}=\dfrac{V_{\text{max}}[S]}{[S]}=V_{\text{max}}=k_2[E]_{\text{total}}[/latex]

The reaction reaches its maximum rate, rate = V_max. The reaction rate depends only on [E]_total and is independent of [S]. This happens when almost all of the enzyme molecules have a substrate molecule in the active site, which means that increasing the concentration of substrate can no longer increase the concentration of enzyme-substrate complex (and thus can no longer increase the rate).

If there is a very small concentration of substrate, [S]≪K_M, we have [S] + K_M ≈ K_M, and the Michaelis-Menten equation becomes first-order in [S]:

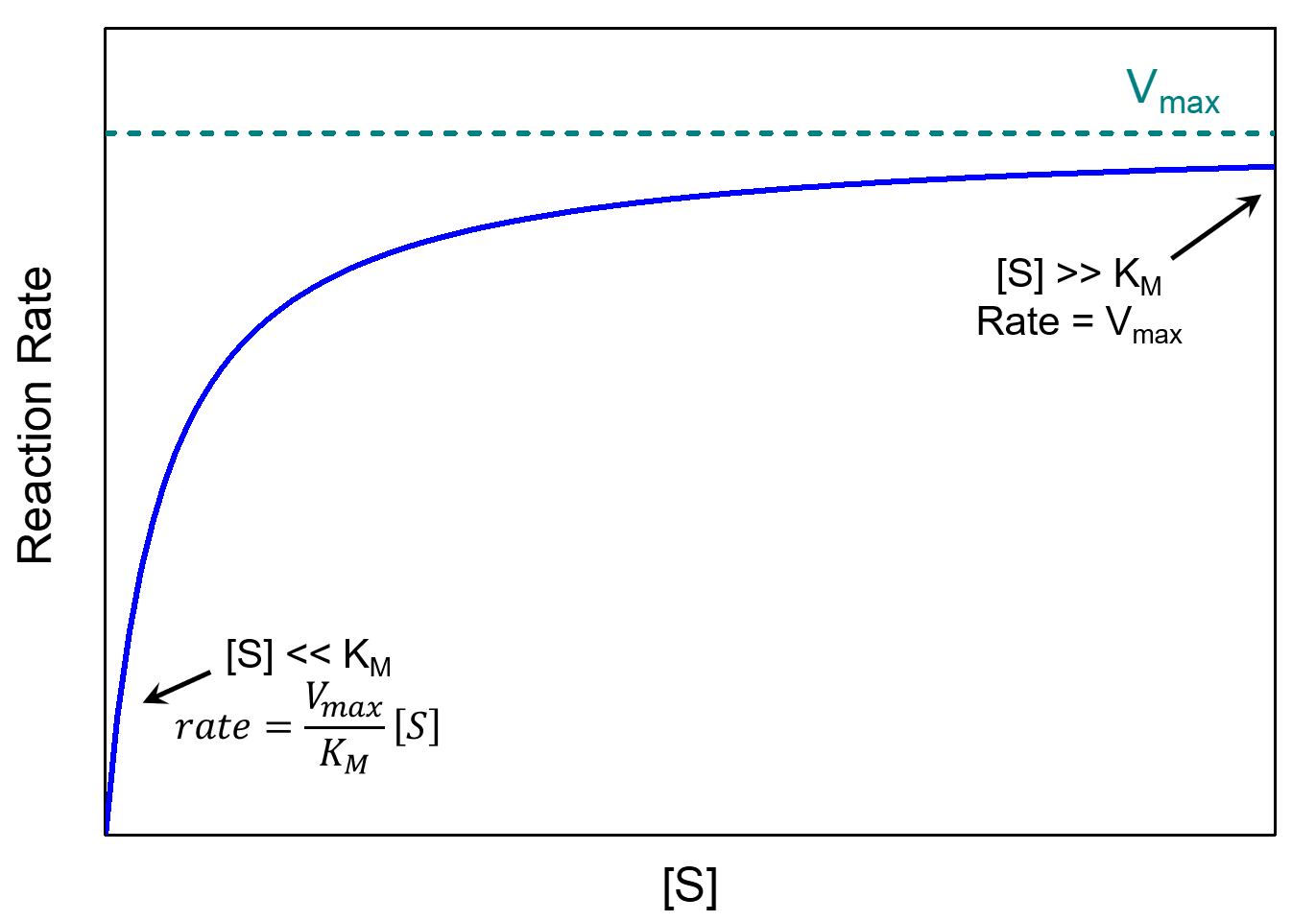
The Michaelis constant is an inverse measure of the substrate’s affinity for the enzyme—a small K_M indicates high affinity, meaning that the rate approaches V_max more quickly. The value of K_M depends on both the enzyme and the substrate, as well as reaction conditions such as temperature and pH.

D24.3 Enzyme Denaturation and Inhibitors

Denaturation is a process in which proteins lose their quaternary, tertiary and secondary structure (see Section D15.6). Enzymes must be folded into the right 3D shape to function. But hydrogen bonds, which play a big part in protein folding, are rather weak, and it does not take much heat, acidity, or other stress to break some hydrogen bonds and denature the enzyme.

Hence, enzyme-catalyzed reactions exhibit an unusual temperature dependence. At relatively low temperatures, the reaction rate increases with temperature, as expected. However, at higher temperatures, the reaction rate drops dramatically due to denaturation of the enzyme, as shown in Figure 4.

Usually enzymes will not denature at temperatures typically encountered by the living organism in which they are found. As a result, enzymes from bacteria living in high-temperature environments such as hot springs are prized by industrial users for their ability to function at high temperatures.

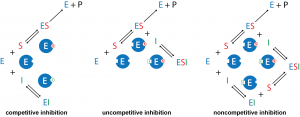
An inhibitor (I) interacts with an enzyme to decreases the enzyme’s catalytic efficiency. An irreversible inhibitor covalently binds to the enzyme’s active site, producing a permanent loss in catalytic efficiency even if the inhibitor’s concentration is later decreased. A reversible inhibitor forms a noncovalent complex with the enzyme, resulting in a temporary decrease in catalytic efficiency. Reducing the concentration of a reversible inhibitor returns the enzyme’s catalytic efficiency to its normal level.

There are several kinds of reversible inhibition. In competitive inhibition the substrate and the inhibitor compete for the same active site on the enzyme. Because the substrate cannot bind to an enzyme–inhibitor complex (EI), the concentration of enzyme available to form enzyme-substrate complex is lower and the enzyme-catalyzed reaction is slower. With uncompetitive inhibition the inhibitor binds to the enzyme-substrate complex but not to the active site, forming an enzyme–substrate–inhibitor (ESI) complex. The formation of an ESI complex decreases catalytic efficiency because some of the enzyme-substrate complex has reacted with inhibitor. This reduces the concentration of ES, which reduces the rate of the rate-limiting step in the mechanism. Finally, in noncompetitive inhibition the inhibitor binds to both the enzyme itself and the enzyme–substrate complex at a site different from the active site. As in uncompetitive inhibition, this forms an inactive ESI complex and reduces the concentration of ES.