Unit Four
Day 27: Thermochemistry and Enthalpy
D27.1 Energy, Temperature, and Heat
Thermal energy is kinetic energy associated with the random motion of atoms and molecules. When thermal energy is transferred into an object, its atoms and molecules move faster on average (higher KEaverage), the object's temperature increases, and we say that the object is “hotter”. When thermal energy is transferred out of an object, its atoms and molecules move more slowly on average (lower KEaverage), the object's temperature decreases, and we say that the object is “colder”.
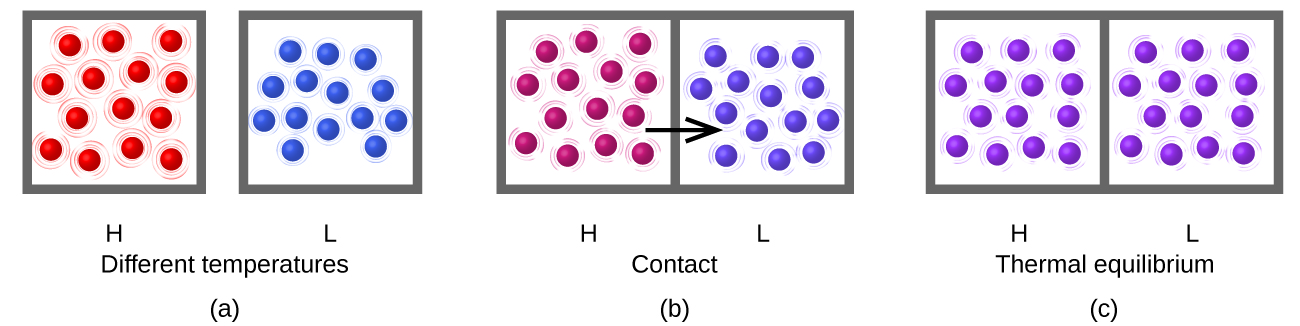
Heating (or heat), represented by q, is the transfer of thermal energy between two bodies at different temperatures (Figure 1).
The heat capacity (C) of an object is the heating required when the object's temperature changes by 1 °C. (Because 1 K is the same size as 1 °C, ΔT has the same numeric value whether expressed in K or °C.) It typically has units of J/°C. Heat capacity depends on both the type and the quantity of substance, and therefore is an extensive property—its value is proportional to the quantity of the substance.
The specific heat capacity (c) of a substance is the heating required to raise the temperature of 1 g of a substance by 1 °C. It typically has units of J/g·°C. Specific heat capacity depends only on the type of substance and therefore is an intensive property. The molar heat capacity, also an intensive property, is the heat capacity per mole of a particular substance and typically has units of J/mol·°C.
Specific heat capacities of some common substances are listed in Table 1.
| Substance | Symbol (state) | Specific Heat Capacity (J/g·°C) |
|---|---|---|
| helium | He(g) | 5.193 |
| water | H2O(l) | 4.184 |
| ethanol | C2H6O(l) | 2.376 |
| ice | H2O(s) | 2.093 (at −10 °C) |
| water vapor | H2O(g) | 1.864 |
| nitrogen | N2(g) | 1.040 |
| oxygen | O2(g) | 0.918 |
| aluminum | Al(s) | 0.897 |
| carbon dioxide | CO2(g) | 0.853 |
| argon | Ar(g) | 0.522 |
| iron | Fe(s) | 0.449 |
| copper | Cu(s) | 0.385 |
| lead | Pb(s) | 0.130 |
| gold | Au(s) | 0.129 |
| silicon | Si(s) | 0.712 |
| Table 1. Specific Heat Capacities of Common Substances at 25 °C and 1 bar | ||
If we know the mass, m, of a sample and its specific heat capacity, c, we can calculate the heat transferred to or from the sample by measuring the temperature change during heating or cooling:
The sign of ΔT tells us whether the substance is being heated (positive value for q) or cooled (negative q ).
Exercise 1: Heat Transfer of Energy
Exercise 2: Specific Heat Capacity and Temperature Change
Exercise 3: Heating a Hot Tub
D27.2 Calorimetry
Calorimetry is an experimental technique used to quantitatively measure heat transfer of energy. Energy is exchanged with a calorimeter, a device with known heat capacity that therefore can relate ΔT to q. A calorimeter must be insulated thermally so that energy does not transfer beyond its physical boundaries. In calorimetry it is useful to define a system, the substance(s) undergoing the chemical or physical change, and the surroundings, everything else that can exchange energy with the system.
For example, if we place a piece of hot metal (M) into cool water (W), heat transfer of energy occurs from metal to water until the two substances reach the same temperature (Figure 2).
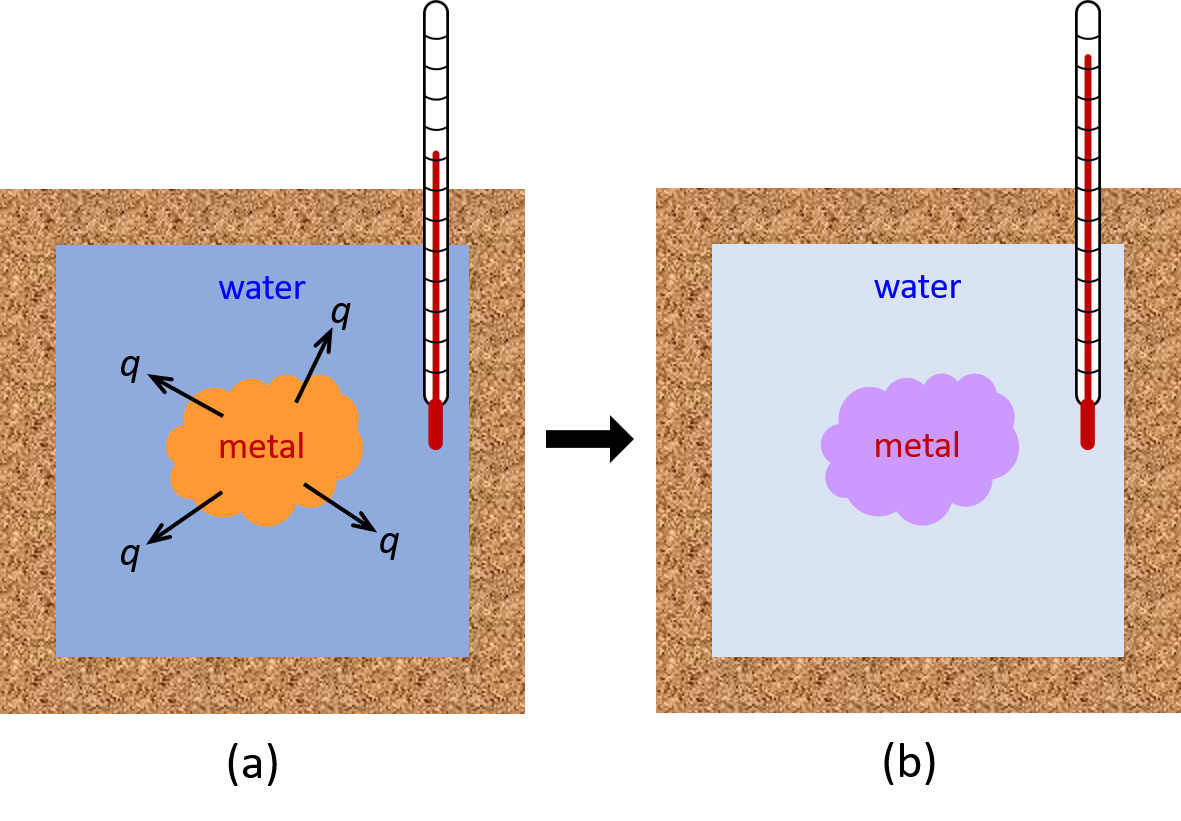
If this occurs in a well insulated calorimeter, this heat transfer would ideally occur only between the two substances. Thus, the magnitude of q is the same for both substances.
The arithmetic sign of q is determined by whether the substance loses or gains energy. In our example, energy is transferred from the metal (qM is negative) to the water (qW is positive).
Exercise 4: Energy Transfer in a Calorimeter
The same principles apply when we apply calorimetry to determine the heat transfer of energy involved in chemical reactions:
Here, qreaction is defined as the change in energy of all atoms present in reactants and products.
A reaction in which there is heat transfer from the reacting substances to their surroundings (a reaction that heats the surroundings) is an exothermic reaction. For example, the combustion reaction that occurs in the flame of a lit match is exothermic. A reaction in which there is heat transfer from the surroundings to the system (a reaction that cools the surroundings) is an endothermic reaction. For example, when the substances in a cold pack (water and a salt such as ammonium nitrate) are mixed, the resulting process transfers energy from the surroundings, making the surroundings colder.
Exercise 5: Energy Transfer to a Cold Pack
If the heat capacity of a calorimeter is too large to neglect or if we require more accurate results, then we must take into account energy transferred to or from the calorimeter as well as energy transfers within the the calorimeter. For example, a type of calorimeter that operates at constant volume, colloquially known as a bomb calorimeter because it involves a strong, steel container that will not explode when an exothermic reaction occurs inside it (the "bomb"). Bomb calorimetry is used to measure energy transfers for reactions such as combustion reactions. The reaction occurs inside the bomb (Figure 3), which is immersed in a water bath and the temperature change of the water bath is measured. Energy has to be transferred to the bomb so the bomb can heat the water, so you need to account for the heat capacity of the bomb as well as the water. That is,
[latex]q_{\text{reaction}} = -[q_{\text{water}} + q_{\text{bomb}}][/latex]

Exercise 6: Bomb Calorimetry
D27.3 Enthalpy
Chemical thermodynamics deals with the relationships between heat, work, and other means of energy transfer in the context of chemical and physical processes. Work, represented by w, is a process that transfers kinetic energy to or from a macroscopic object. When a golf club strikes a golf ball, for example, the club does work on the ball, accelerating the ball to a high speed.
Substances act as reservoirs of energy. The total of all possible kinds of energy present in a substance is called the internal energy (U). (The symbol U, instead of E, represents a sum over several different kinds of energy within the substance.) Energy is transferred into a system when it is heated (q) by the surroundings or when the surroundings does work (w) on the system. For example, energy can be transferred into room-temperature metal wire if it is immersed in hot water (the water heats the wire), or if you rapidly bend the wire back and forth (the wire becomes warmer because of the work done on it). Both processes increase the internal energy of the wire, which is reflected in an increase in the wire’s temperature.
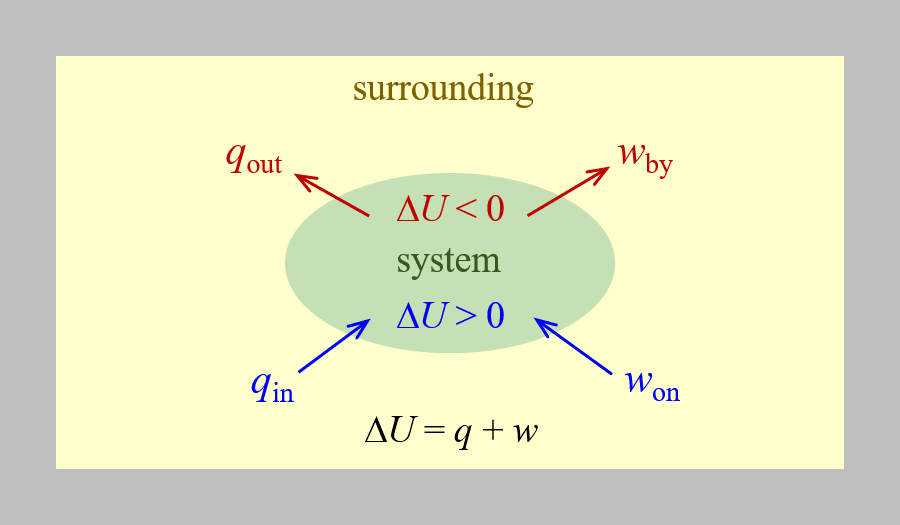
The relationship between internal energy, heat, and work can be represented by the equation:
assuming there are no energy transfers other than heat and work. This is one version of the first law of thermodynamics, the law of conservation of energy. The equation shows that the internal energy of a system changes through heat transfer into or out of the system (positive q is heat transfer in; negative q is heat transfer out) or work done on or by the system. The work, w, is positive if it is done on the system (increases the system's internal energy) and negative if it is done by the system. This is summarized in the figure below.
Chemists ordinarily use a property known as enthalpy (H) to describe the thermodynamics of chemical and physical processes. Enthalpy is defined by this equation:
where P is pressure and V is volume. Enthalpy is closely related to energy, differing by the quantity PV.
Enthalpy values for specific substances cannot be measured directly. Only enthalpy changes for chemical or physical processes can be determined. For processes that take place at constant pressure (a common condition for many chemical and physical changes that take place at atmospheric pressure), the enthalpy change (ΔH) is:
(where P is factored out of Δ(PV) because P is constant).
The mathematical product PΔV represents pressure-volume work, also called expansion work. For example, consider a gas (the system) confined in a cylinder by a piston, as shown in the figure. The pressure exerted by the gas results from many collisions of gas molecules with the bottom of the piston and the walls of the cylinder. If the pressure of the gas causes the piston to move upward, the gas does work on the piston (part of the surroundings). This reference shows that the work done by the system on the surroundings equals PΔV. Work done by the system is the negative of w, which is defined as work done on the system, so
Substituting yields:
| ΔH | = | ΔU + PΔV |
| = | (qP + w) - w | |
| = | qP |
where qp is the heat of reaction under constant pressure. Therefore, if a chemical or physical process is carried out at constant pressure with the only work done caused by expansion or contraction, then the heat transfer of energy (qp) equals the enthalpy change (ΔH) for the process.
The heat transfer to the surroundings when you operate a Bunsen burner is equal to the enthalpy change of the methane combustion reaction that takes place, because the reaction occurs at the essentially constant pressure of the atmosphere. Chemists usually perform experiments under normal atmospheric conditions, at constant external pressure with qp = ΔH, which makes enthalpy the most convenient choice for determining heat transfer of energy as a result of a chemical reaction. The enthalpy change for a chemical reaction is symbolized ΔrH, where the subscript r indicates that the change is for a reaction.
On the other hand, the heat transfer of energy by a reaction measured in a bomb calorimeter is not equal to ΔH because the closed, constant-volume metal container prevents expansion work from occurring. In a constant-volume system w = 0 and ΔU = qv + w = qv, where the subscript v indicates constant volume.
D27.4 Standard-state Reaction Enthalpy Change, ΔrH°
Heat effects of a chemical reaction are summarized in thermochemical expressions, balanced chemical equations together with values of ΔrH°, the standard-state reaction enthalpy change, and a temperature. The standard-state reaction enthalpy change, ΔrH°, is the standard-state enthalpy of pure, unmixed products minus the standard-state enthalpy of pure, unmixed reactants; that is, the enthalpy change for the reaction under standard-state conditions.
ΔrH° = H°(products) - H°(reactants)
A standard state is a commonly accepted set of conditions used as a reference point. For chemists, the standard state refers to substances under a pressure of 1 bar and solutions at a concentration of 1 mol/L (1 M). (Note that some thermochemical tables may list values with a standard state of 1 atm. Because 1 bar = 0.987 atm, thermochemical values are nearly the same under both sets of standard conditions; however, for accurate work the standard state should be checked.)
The standard state does not specify a temperature. Because ΔrH° can vary with temperature, temperature is typically specified in a thermochemical expression.
We will include a superscript “º” to designate standard state. Thus, the symbol [latex]{\Delta}_\text{r}H^{\circ}_{\text {298 K}}[/latex] indicates an enthalpy change for a process occurring under standard-state conditions and at 298 K.
For example, consider this thermochemical expression:
2 H2(g) + O2(g) ⟶ 2 H2O(g) ΔrH° = 8.031 × 10−22 kJ = −483.6 kJ/mol (25 °C)
This refers to reaction of two molecules of hydrogen with 1 molecule of oxygen to form two molecules of water, all in the gas phase at 1 bar pressure. If this reaction equation took place once, the two hydrogen molecules and the one oxygen molecule would react to form two water molecules and 8.031 × 10−22 kJ would be transferred to the surroundings. Because we are interested in laboratory-scale reactions, where moles of reactants are involved, ΔrH° is always reported per mole of reaction rather than for a single reaction event. A mole of reaction involves a chemical reaction equation happening 6.022 × 1023 times; in this case that is 2 mol H2(g) reacting with 1 mol O2(g) to give 2 mol H2O(g). The heat transfer of energy to the surroundings is then 8.031 × 10−22 kJ × 6.022 × 1023 mol−1 = 483.6 kJ/mol. Because the energy transfer is from system to surroundings, the sign is negative and ΔrH° = −483.6 kJ/mol.
These conventions apply to thermochemical expressions:
- In a thermochemical expression, the listed ΔrH° value indicates the heat transfer of energy for the coefficients in the chemical equation. If the coefficients are multiplied by some factor, ΔrH° must be multiplied by that same factor. In other words, ΔrH° is an extensive property. For example:
2 H2(g) + O2(g) ⟶ 2 H2O(g) ΔrH° = −483.6 kJ/mol two-fold increase: 4 H2(g) + 2 O2(g) ⟶ 4 H2O(g) ΔrH° = 2(−483.6 kJ/mol) = -967.2 kJ/mol two-fold decrease: H2(g) + ½ O2(g) ⟶ H2O(g) ΔrH° = ½(−483.6 kJ/mol) = -241.8 kJ/mol - ΔrH° of a reaction depends on the physical state of the reactants and products (whether we have gases, liquids, solids, or aqueous solutions), so physical states must be shown.
- A negative ΔrH° indicates an exothermic reaction; a positive ΔrH° indicates an endothermic reaction. If the direction of a chemical equation is reversed, the arithmetic sign of its ΔrH° is changed. (A process that is endothermic when reactants change into products is exothermic when products change into reactants).
Be sure to take both stoichiometry and limiting reactants into account when determining the ΔrH° for a chemical reaction.
Exercise 7: Standard-state Reaction Enthalpy
D27.5 Bond Enthalpy and Reaction Enthalpy Change
The enthalpy change for a gas-phase chemical reaction, ΔrH, equals the sum of the enthalpy required to break each of the bonds in the reactant molecules (energy in, positive sign) plus the sum of the enthalpy released when each of the bonds in the product molecules forms (energy out, negative sign). This can be expressed mathematically as:
ΔrH = ∑Ebonds broken - ∑Ebonds formed
Because the bond enthalpy values provided in the Appendix are averaged over many different molecules for each type of bond, this calculation is not exact, but it provides a good estimate for the enthalpy change of any specific reaction. Also, bond enthalpy calculations assume that all molecules are far from each other (which means that reactants and products must be in the gas phase). Additional enthalpy changes occur when a gas condenses to a liquid or solid or dissolves into a solution; these transformations are not accounted for by bond enthalpies.
Consider this balanced reaction:
H2(g) + Cl2(g) → 2 HCl(g)
One H–H bond (436 kJ/mol) and one Cl–Cl bond (242 kJ/mol) are broken; two H-Cl bonds (431 kJ/mol each) are formed. Representing bond enthalpies by Dbond, we have:
ΔrH = [436 kJ/mol + 242 kJ/mol] - 2(431 kJ/mol) = -184 kJ/mol
There are the same number of bonds formed as were broken. Because the bonds in the products are stronger than those in the reactants, the reaction has a net release (negative sign) of about 184 kJ for every mole of reaction as written. The energy released increases the temperature of the surroundings (the reaction is exothermic).
Here are two general rules to predict whether a chemical reaction releases energy (is exothermic):
- If there are more bonds in the product molecules than in the reactant molecules and the bonds have about the same strength, the reaction is exothermic.
- If there are stronger bonds in the product molecules than in the reactant molecules and the number of bonds is the same in reactants and products, the reaction is exothermic.
Exercise 8: Enthalpy Change from Bond Enthalpies
Check Your Learning
D27.6 Hess’s Law
The enthalpy change for a particular reaction is the same regardless of which or how many steps the reaction is carried out in. This conveniently allows us to calculate the heat transfer for a chemical change from other experimentally determined enthalpy changes. This type of calculation usually involves Hess’s law: If a process can be written as the sum of several stepwise processes, the enthalpy change of the total process equals the sum of the enthalpy changes of the various steps.
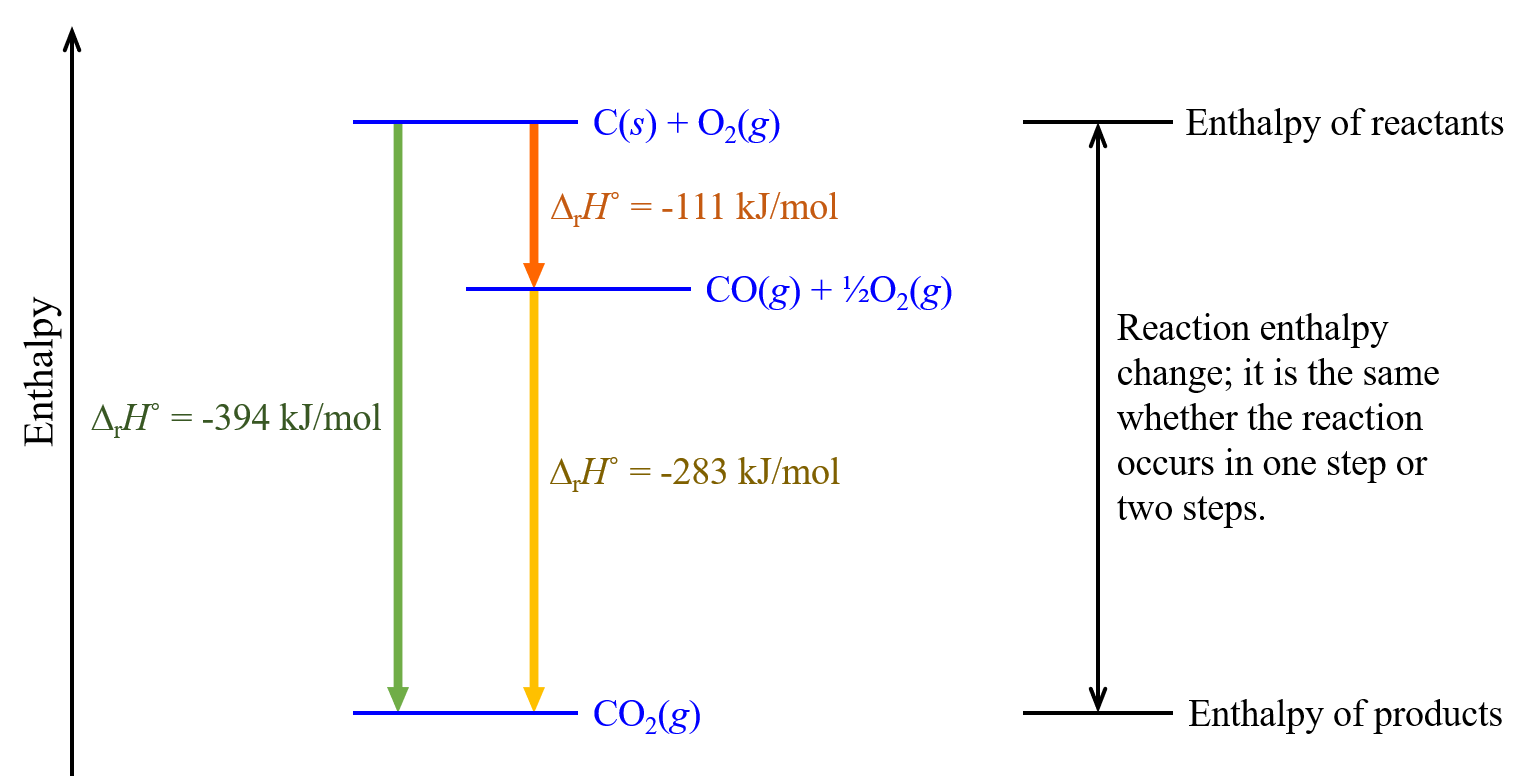
For example, we can think of this reaction occurring in a single step:
or in a two-step process:
| step 1: | C(s) + ½O2(g) | ⟶ | CO(g) | ΔrH° = -111 kJ/mol |
| step 2: | CO(g) + ½O2(g) | ⟶ | CO2(g) | ΔrH° = -283 kJ/mol |
According to Hess’s law, the ΔrH° of the one-step reaction equals the sum of the ΔrH° of the two steps in the two-step reaction:
| step 1: | C(s) + ½O2(g) | ⟶ | CO(g) | ΔrH° = -111 kJ/mol |
| step 2: | CO(g) + ½O2(g) | ⟶ | CO2(g) | ΔrH° = -283 kJ/mol |
| Sum: | C(s) + O2(g) | ⟶ | CO2(g) | ΔrH° = -394 kJ/mol |
This concept is illustrated in Figure 4.
D27.7 Standard Enthalpy of Formation
Standard enthalpy of formation, ΔfH°, is the enthalpy change for a reaction in which exactly one mole of a pure substance in a specified state (s, l, or g) is formed from free elements in their most stable states under standard-state conditions. ΔfH° is also referred to as the standard heat of formation.
For example, ΔfH° of CO2(g) at 25 °C is −393.5 kJ/mol. This is the enthalpy change for the exothermic reaction:
The gaseous reactant and product are at a pressure of 1 bar, the carbon is present as graphite, which is the most stable form of carbon under standard conditions.
For nitrogen dioxide, NO2(g), ΔfH° is 33.2 kJ/mol at 25 °C:
A reaction equation with ½ mole of N2 and 1 mole O2 is appropriate in this case because the standard enthalpy of formation always refers to formation of 1 mol NO2(g).
By definition, the standard enthalpy of formation of an element in its most stable form is 0 kJ/mol under standard conditions. A table of ΔfH° values for many common substances can be found in the Appendix.
Exercise 9: Equations for Standard Formation Enthalpy
Hess’s law can be used to determine the ΔrH° of any reaction if the ΔfH° of the reactants and products are available. In other words, we can think of any reaction as occurring via step-wise decomposition of the reactants into their component elements followed by re-combination of the elements to give the products. (Almost no reaction would actually occur via such a mechanism because some of the reactions would have large activation-energy barriers and consequently very small rates, but we can imagine such a path for the sole purpose of using Hess's law to calculate ΔrH°.)
The ΔrH° of the overall reaction is therefore equal to:
Exercise 10: Using Standard Formation Enthalpies
Activity 1: Applying Hess's Law to Standard Formation Enthalpies
Podia Question
Chlorine monofluoride can react with fluorine to form chlorine trifluoride:
(i) [latex]\text{ClF}(g) + \text{F}_2(g) \longrightarrow \text{ClF}_3(g) \;\;\;\;\; \Delta _\text{r}H\text{°}= \;?[/latex]
Use the reactions here to determine the ΔrH° for reaction (i):
(ii) [latex]2\text{OF}_2(g) \longrightarrow \text{O}_2(g) + 2\text{F}_2(g) \;\;\;\;\; \Delta _\text{r}H\text{°}_{(ii)} = -49.4 \;\text{kJ/mol}[/latex]
(iii) [latex]2\text{ClF}(g) + \text{O}_2(g) \longrightarrow \text{Cl}_2 \text{O}(g) + \text{OF}_2(g) \;\;\;\;\; \Delta _\text{r}H\text{°}_{(iii)} = +205.6 \;\text{kJ/mol}[/latex]
(iv) [latex]\text{ClF}_3(g) + \text{O}_2(g) \longrightarrow \frac{1}{2}\text{Cl}_2 \text{O}(g) + \frac{3}{2} \text{OF}_2(g) \;\;\;\;\; \Delta _\text{r}H\text{°}_{(iv)} = +266.7 \;\text{kJ/mol}[/latex]
Two days before the next whole-class session, this Podia question will become live on Podia, where you can submit your answer.

