D36.1 Buffer Solutions

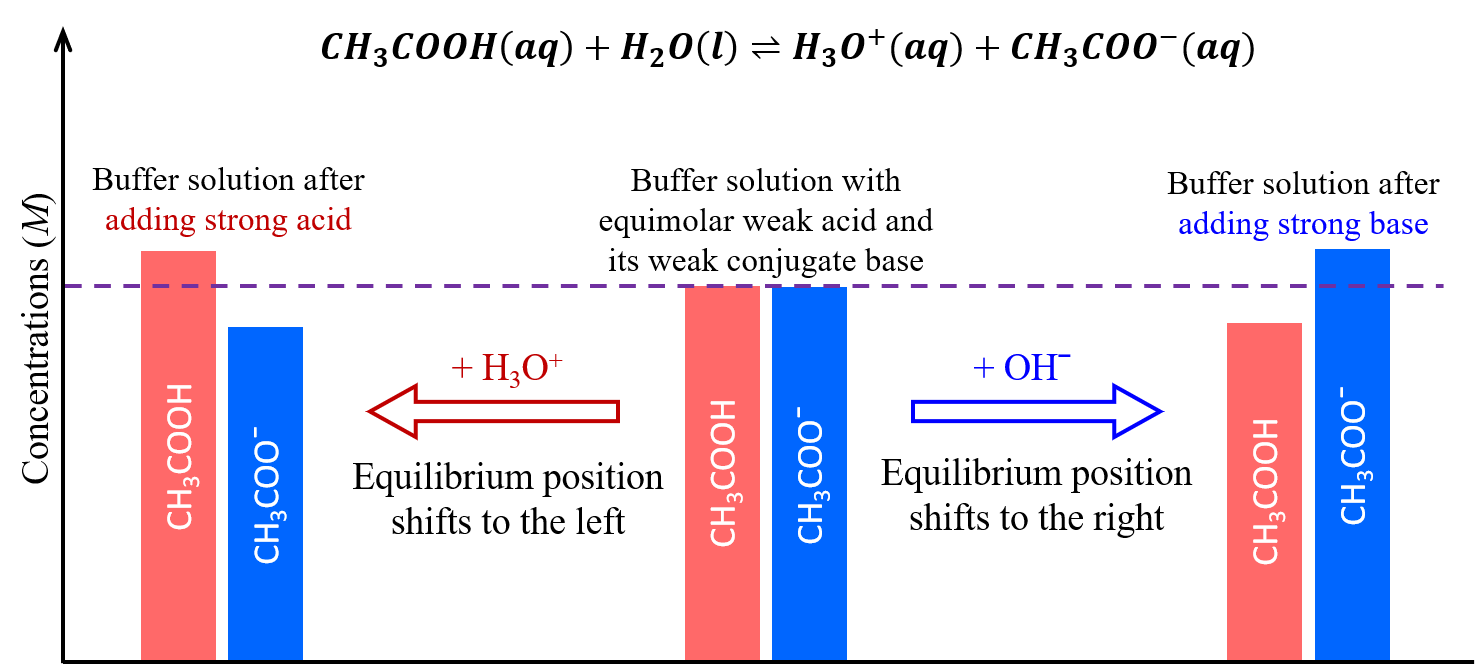
A mixture of a weak acid and its conjugate base, such as acetic acid and sodium acetate (CH₃COOH + CH₃COONa), or a mixture of a weak base and its conjugate acid, such as ammonia and ammonium chloride (NH₃ + NH₄Cl), is a buffer solution. A buffer solution resists changes in pH when small amounts of a strong acid or a strong base are added (Figure 1).

A solution of equal concentrations of CH₃COOH and CH₃COONa is slightly acidic because the K_{a,acetic acid} > K_{b, acetate anion}. When a strong base, such as NaOH, is added to this solution, the OH^– anions react with the few H₃O⁺ cations, decreasing concentrations of H₃O⁺. This shifts the following equilibrium to the right:

restoring H₃O⁺ concentration to almost the value it had before the NaOH was added. The net effect of most of the added NaOH is to convert some of the weak acid, CH₃COOH, to a weak base, CH₃COO⁻:

Hence, there is only a minimal decrease in H₃O⁺ concentration.

When a strong acid, such as HCl, is added, the net effect of most of the added H₃O⁺ is to convert acetate anions to acetic acid molecules:

And again, there is only a minimal increase in H₃O⁺ concentration.

As illustrated in Figure 2, a buffer solution can moderate changes to pH because it consists of a weak acid that can react with added strong base as well as a weak base that can react with added strong acid.

The weak base and weak acid in a buffer solution are typically a conjugate acid-base pair, which maintains one dynamic equilibrium that responds to additions of other acids and bases. If they are not a conjugate acid-base pair, then there would be two dynamic equilibria at play, which significantly complicates the buffering actions.

D36.2 Henderson-Hasselbalch Equation

The ionization constant expression for a weak acid HA is:

Rearranging gives:

Taking the negative logarithm of both sides, we have:

It is much more convenient to deal with the initial concentrations of the weak acid and weak base when preparing a buffer solution. (The initial concentration is the amount of weak acid and weak base added to the solution mixture divide by the volume.) Therefore:

“x” is the increase in concentration of H₃O⁺ as the solution reaches equilibrium (see activity 1 above) and [HA]₀ and [A⁻]₀ are the concentration of HA and A⁻ before any reaction occurs. When the approximation that x is at least 100 times smaller than the concentrations of HA and A⁻ is valid, we have the Henderson-Hasselbalch equation:

[latex]\text{pH} = \text{p}K_a\;+\;\text{log}\dfrac{[\text{A}^{-}]_0}{[\text{HA}]_0}[/latex]

Note that when [A−]₀ = [HA]₀, pH = pK_a + log(1) = pK_a.

The Henderson-Hasselbalch equation can be used to calculate the buffer solution pH, given the K_a and the initial concentrations, or it can be used to determine the ratio of initial concentrations of weak acid and base required to achieve a desired pH.

The Henderson-Hasselbalch equation applies only to buffer solutions in which the ratio [latex]\dfrac{[\text{A}^{-}]_0}{[\text{HA}]_0}[/latex] is between 0.1 and 10. If enough strong acid or strong base is added to the buffer solution to exceed this range, the pH begins to change significantly (in other words, the solution is no longer a buffer solution).

D36.3 Selection of a Suitable Buffer

A buffer solution moderates changes in pH because it contains both a weak acid that can react with added strong base and a weak base that can react with added strong acid. This leads to several criteria for selecting a suitable buffer solution for a given purpose.

1. The pK_a of the weak acid in the buffer should be close to the desired pH of the buffer solution. According to the Henderson-Hasselbalch equation, if the concentrations of weak acid and weak base are equal, the pH of the buffer solution equals the pK_a of the weak acid involved.
2. A buffer solution should have approximately equal concentrations of the weak acid and weak base. A [latex]\dfrac{[\text{A}^{-}]_0}{[\text{HA}]_0}[/latex] ratio of >10 or <0.1 makes for a poor buffer solution. Figure 3 shows how the pH of an acetic acid-acetate ion buffer increases as strong base is added. The initial pH is pK_a = 4.74. When pH reaches 5.74, a change of 1 pH unit, the ratio [latex]\dfrac{[\text{acetic acid}]}{[\text{acetate anion}]} = 0.11 = 11\text{%}[/latex]. After that the pH increases more rapidly and the solution no longer provides significant buffering.
   

   

3. The larger the amounts (mol) of weak acid and weak base are the greater is the amount (mol) of strong base or strong acid that can be added before there is a significant change in pH .

When designing a buffer system, look for weak conjugate acid-base pairs that have pK_a of the weak acid near the desired pH. Then adjust the ratio of the weak base to weak acid concentrations to achieve the exact pH desired. Make certain that the concentrations of weak base and weak acid are large enough to react with the quantities of acid or base that might be added to the buffer solution.

D36.4 Buffer Capacity

We can see how a buffer solution works by comparing quantitatively the pH of a buffered solution with the pH of a unbuffered solution upon addition of a strong acid or base.

We can see from the above activities that the change in pH is much more significant in the unbuffered solution compared to the buffered solution.

However, buffer solutions do not have an unlimited capacity to keep the pH relatively constant (Figure 4). For example, if we add sufficient strong base to a buffer that all the weak acid has reacted, no more buffering action toward the base is possible. Similarly, if we add an excess of strong acid, the weak base would all be reacted, and no more buffering action toward any additional acid would be possible. In fact, we do not even need to react away all the weak acid or base in a buffer to make significant change in pH: buffering action diminishes rapidly as a given component nears depletion. This was seen in Figure 3 in the above section, where reducing the concentration of weak acid to 11% of the concentration of weak base caused a change of 1 pH unit. The curve in Figure 3 goes up rapidly after that, indicating that the buffer has been “broken” and no longer resists changes in pH.

The buffer capacity is the amount (mol) of acid or base that can be added to a given volume of a buffer solution before the pH changes by ±1 from the pK_a of the weak acid. (Recall that if equal concentrations of weak acid and conjugate base are in a buffer solution, pH = pK_a.)

Buffer capacity depends on the amount (mol) of weak acid and its conjugate base that are in a buffer mixture. For example, a 1 L solution of 1.0 M CH₃COOH and 1.0 M CH₃COONa has a greater buffer capacity than a 1 L solution of 0.10 M CH₃COOH and 0.10 M CH₃COONa, even though both solutions have the same pH. The first solution has more buffer capacity because it contains more moles of acetic acid and acetate ion.

It takes 0.82 mol HCl to change the buffer pH from 4.74 to 3.74 in the first solution:

On the other hand, for the solution where the concentrations of weak acid and conjugate base are 0.10 M, it takes only one-tenth as much HCl, 0.082 mol HCl, to change the buffer pH from 4.74 to 3.74:

If a buffer solution does not have equal concentrations of weak acid and weak base, the buffer capacity when strong acid is added is different from the buffer capacity when strong base is added.