Unit Five
Day 38: Oxidation-Reduction Reactions, Voltaic Cells
D38.1 Oxidation-reduction Reactions and Electrochemistry
Electrochemistry deals with chemical reactions that involve transfer of electron density; in other words, the reactions either produce electricity or are caused by passage of electrical current through matter. These reactions are called oxidation-reduction (abbreviated redox) reactions.
Here’s a brief list of units and definitions used when discussing redox reactions and their applications.
- The SI unit of electric charge is the coulomb, C.
- The elementary unit of charge is the charge of a single electron, which is equal to 1.602 × 10−19 C.
- Movement of electrons (or ions) carries electric charges from one place to another, and the quantity of such charge transferred per unit time is the electric current.
- Current has the SI unit ampere, A, which is the transfer of one coulomb per second (1 A = 1 C/s).
- Typically, electric current flows in a closed path, called an electric circuit.
- It is necessary to maintain a closed circuit for current to flow. If the circuit is open, current will not flow.
- Electrical potential, SI unit volt, V, is the ability of an electric field to do work on a charge.
- A flow of charge is caused by an electrical potential difference between two points in the circuit.
- When 1 coulomb of charge moves through a potential difference of 1 volt, it gains or loses 1 joule of energy (1 J = 1 C × 1 V).
- Electric power is the quantity of energy transferred per unit time and is measured in watts, W (1 W = 1 J / 1 s).
Exercise 1: Electric Energy and Flow of Charge
D38.2 Redox Reactions and Oxidation Number
Some redox reactions involve transfer of electrons between reactant atoms to yield ionic products. For example, formation of a crystal lattice of sodium chloride (a lattice of Na+ ions and Cl− ions) requires transfer of electrons from sodium atoms to chlorine atoms:
It is useful to consider the electron transfer as two concurrent processes. The processes are called half-reactions, one in which electrons are lost and one in which electrons are gained. The half-reactions for reaction of sodium with chlorine are:
| 2Na(s) | ⟶ | 2Na+(s) + 2e− |
| Cl2(g) + 2e− | ⟶ | 2Cl−(s) |
The half-reactions allow us to see that the number of electrons lost equals the number of electrons gained—we cannot create or destroy electrons in a chemical reaction. The half-reactions also show which species gains electrons (Cl atoms in Cl2) and which species loses electrons (Na atoms). The species that loses electrons is said to be oxidized and the loss of electrons is called oxidation; the species that gains electrons is said to be reduced and the gain of electrons is called reduction.
The species that causes reduction to occur is called the reducing agent (or reductant). In this reaction sodium is the reducing agent because it causes Cl2 to gain electrons. The species that causes oxidation to occur is called the oxidizing agent (or oxidant). In this reaction chlorine functions as an oxidant, causing sodium to lose electrons.
Some redox processes do not involve obvious transfer of electrons because no ions are involved in the reaction. For example:
To systematically classify redox reactions of all types, we define oxidation number (or oxidation state) of an element in a compound as the charge its atoms would possess if the compound was ionic, that is, if all electrons in each polar covalent bond were assigned to the more electronegative atom.
The steps below can be used to assign oxidation numbers to each element in a compound.
- The oxidation number of an atom in an elemental substance is zero.
- The oxidation number of a monoatomic ion is equal to the ion’s charge.
- The sum of oxidation numbers over all atoms in a neutral compound is zero.
- The sum of the oxidation numbers over all atoms in a polyatomic ion equals the ion’s charge. If a compound includes more than one polyatomic ion, the oxidation number of an atom in one ion can differ from the oxidation number in the other polyatomic ion.
- Atoms of some elements have the same oxidation number in almost all compounds.
- Fluorine always has oxidation number −1 when present in a compound
- Atoms of alkali metals (Li, Na, K, Rb, Cs) have oxidation number +1 in nearly all compounds
- Atoms of alkaline earth metals (Be, Mg, Ca, Sr, Ba) have oxidation number +2 in nearly all compounds
- Hydrogen has oxidation number +1 when combined with nonmetals, −1 when combined with metals
- Apply these two rules only if rules 1-5 have not determined all oxidation numbers.
- Oxygen has oxidation number −2 unless rules 1-5 have already given O a different oxidation number
- In binary compounds of nonmetals, the more electronegative element is given a negative oxidation number equal to the charge on its monoatomic ion; for example in PCl3, the more electronegative Cl is assigned oxidation number −1 and P is assigned +3 (by rule 3).
Activity 1
Exercise 2: Assigning Oxidation Numbers
Using oxidation numbers we can identify redox reactions by looking for one or more elements whose oxidation numbers change during the course of the reaction. When its oxidation number increases, an element has been oxidized; when its oxidation number decreases, the element has been reduced.
In this reaction
sodium is oxidized (its oxidation number increases from 0 in Na to +1 in NaCl) and chlorine is reduced (its oxidation number decreases from 0 in Cl2 to −1 in NaCl).
In this reaction
hydrogen is oxidized (its oxidation number increases from 0 in H2 to +1 in HCl) and chlorine is reduced (its oxidation number decreases from 0 in Cl2 to −1 in HCl).
Several subclasses of redox reactions can be identified. One example is combustion reactions in which the reductant (fuel) and oxidant (often, O2) react vigorously and produce significant temperature increase, often in the form of a flame. Another class of redox reaction is a rocket propellant reaction such as this one in which solid aluminum is oxidized by ammonium perchlorate:
Exercise 3: Recognizing Oxidation-Reduction Reactions
Exercise 4: Recognizing Oxidizing and Reducing Agents
For the reaction below, identify which species is oxidized and which is reduced, and identify the oxidizing agent and the reducing agent.
[Enter your answers without subscripts, superscripts, or states, and put charges in parentheses. For example, SO42-(aq) would be entered as SO4(2-).]
D38.3 Balancing Redox Reactions
Redox reactions frequently occur in aqueous solutions, which can be acidic, basic, or neutral. Moreover, H2O molecules may actively participate in the reaction, and depending on the conditions, H3O+ (present under acidic conditions) and OH− (present under basic conditions) may also be a reactant or a product.
Half-reactions make it easier to balance redox reactions because you can balance the oxidation half-reaction separately from the reduction half-reaction, and make certain that the number of electrons lost in the oxidation process equals the number of electrons gained in the reduction process.
We will balance an example redox reaction in acidic solution and one in basic solution to illustrate the process of balancing redox reactions, and highlight how the nature of the solution can play a role. (A neutral solution may be treated as acidic or basic, though treating it as acidic is usually easier.)
Acidic Solution
Consider the unbalanced reaction:
where iron underwent oxidation because Fe2+ has lost an electron to become Fe3+, and manganese underwent reduction because it gained five electrons to change from an oxidation state of +7 to an oxidation state of +2.
| Oxidation (unbalanced): | Fe2+(aq) | ⟶ | Fe3+(aq) |
| Reduction (unbalanced): | MnO4‾(aq) | ⟶ | Mn2+(aq) |
For redox reactions, it is a useful simplification to represent H3O+(aq) as H+(aq)—where there is a need for balancing O atoms, we can involve H2O(l), and then use H+(aq) to balance the H atoms.
For instance, in the above reduction half-reaction, there are four O atoms on the left side and none on the right side. To balance the elements, we can add 4 H2O(l) to the product side, and then to balance H atoms, add 8 H+(aq) to the reactant side:
Once the atoms have been balanced, we need to balance the electric charge for each half-reaction. For the oxidation half-reaction, the total charge on the left side is +2 and the total charge on the right side is +3, so charge is unbalanced. We use electrons to balance the charge. Adding a single electron on the right side gives a balanced oxidation half-reaction:
In oxidation half-reactions, electrons appear on the right side of the equation. Because iron is oxidized, iron is the reducing agent in this redox reaction.
You should always check that the half-reaction is balanced for the number of atoms of each element and the total charge:
| Fe: | (1 atom in Fe2+)·(1 Fe2+) = 1 | ⟶ | (1 atom in Fe3+)·(1 Fe3+) = 1 | 1 = 1 ✓ |
| Charge: | 1·(+2) = +2 | ⟶ | 1·(+3) + 1·(-1) = +2 | +2 = +2 ✓ |
If the atoms and charges are balanced, then the half-reaction itself is balanced.
For the reduction half-reaction, we have balanced the atoms but not the charge. The total charge on the reactant-side is +7, the total charge on the product-side is +2. Therefore, it is necessary to add five electrons to the left side to achieve charge balance:
In all reduction half-reactions, electrons appear on the left side. The species that was reduced, MnO4−, is the oxidizing agent in this redox reaction.
Again, check that the half-reaction is balanced for the number of atoms of each element and the total charge:
| Mn: | (1 atom in MnO4−)·(1 MnO4−) = 1 | ⟶ | (1 atom in Mn2+)·(1 Mn2+) = 1 | 1 = 1 ✓ |
| O: | (4 atoms in MnO4−)·(1 MnO4−) = 4 | ⟶ | (1 atom in H2O)·(4 H2O) = 4 | 4 = 4 ✓ |
| H: | (1 atom in H+)·(8 H+) = 8 | ⟶ | (2 atoms in H2O)·(4 H2O) = 8 | 8 = 8 ✓ |
| Charge: | 1·(-1) + 8·(+1) + 5·(-1) = +2 | ⟶ | 1·(+2) + 4·(0) = +2 | +2 = +2 ✓ |
We now have two balanced half-reactions:
| Oxidation: | Fe2+(aq) | ⟶ | Fe3+(aq) + e‾ |
| Reduction: | MnO4−(aq) + 8H+(aq) + 5e− | ⟶ | Mn2+(aq) + 4H2O(l) |
The key to combining the half-reactions is the electrons: the number of electrons generated by the oxidation half-reaction must equal the number of electrons consumed by the reduction half-reaction. Here, the oxidation half-reaction generates one electron, while the reduction half-reaction requires five. The lowest common multiple of one and five is five. Therefore, it is necessary to first multiply the oxidation half-reaction by five and the reduction half-reaction by one, then sum the resulting half-reactions:
| Oxidation: | 5 × (Fe2+(aq) | ⟶ | Fe3+(aq) + e‾) |
| Reduction: | MnO4−(aq) + 8 H+(aq) + 5e− | ⟶ | Mn2+(aq) + 4 H2O(l) |
| overall: | 5 Fe2+(aq) + MnO4−(aq) + 8 H+(aq) | ⟶ | 5 Fe3+(aq) + Mn2+(aq) + 4 H2O(l) |
This is the overall balanced equation in acidic solution. Electrons do not appear in the overall reaction equation because all electrons lost in the oxidation half-reaction are gained in the reduction half-reaction. On each side of the overall equation there should be the same number of atoms of each element and the same total electric charge. Be sure to carefully check each side to verify everything has been balanced correctly.
Basic Solution
The simplest way to balance redox reaction in basic solution is to start with the balanced equation in acidic solution, then “convert” H+(aq) to OH−(aq) (there is an excess of OH− ions instead of H3O+ ions in basic solutions). For example, when balancing the following reaction in basic solution:
start by collecting the species given into unbalanced oxidation and reduction half-reactions:
| Oxidation (unbalanced): | Cr(OH)3(s) | ⟶ | CrO42-(aq) |
| Reduction (unbalanced): | MnO4‾(aq) | ⟶ | MnO2(s) |
For the oxidation half-reaction, we can add one H2O molecule to the left side to balance oxygen atoms, and then balance hydrogen atoms with five H+(aq) on the right side (again, we do the initial balancing by assuming acidic solution):
The left side of the equation has a total charge of 0, and the right side a total charge of +3. Adding three electrons to the right side produces a mass- and charge-balanced oxidation half-reaction (in acidic solution):
Checking the half-reaction:
| Cr: | (1 atom in Cr(OH)3)·(1 Cr(OH)3) = 1 | ⟶ | (1 atom in CrO42-)·(1 CrO42-) = 1 | 1 = 1 ✓ |
| O: | (3 atoms in Cr(OH)3)·(1 Cr(OH)3) + (1 atom in H2O)·(1 H2O) = 4 | ⟶ | (4 atoms in CrO42-)·(1 CrO42-) = 4 | 4 = 4 ✓ |
| H: | (3 atoms in Cr(OH)3)·(1 Cr(OH)3) + (2 atoms in H2O)·(1 H2O) = 5 | ⟶ | (1 atom in H+)·(5 H+) = 5 | 5 = 5 ✓ |
| Charge: | 1·(0) + 1·(0) = 0 | ⟶ | 1·(-2) + 5·(+1) + 3·(-1) = 0 | 0 = 0 ✓ |
For the reduction half-reaction, we need two H2O molecules on the right to balance oxygen atoms. Then to balance hydrogen atoms, we need to add four H+(aq) on the left:
Then add three electrons to the left side to balance the charge:
Make sure to check the half-reaction:
| Mn: | (1 atom in MnO4–)·(1 MnO4–) = 1 | ⟶ | (1 atom in MnO2)·(1 MnO2) = 1 | 1 = 1 ✓ |
| O: | (4 atoms in MnO4–)·(1 MnO4–) = 4 | ⟶ | (2 atoms in MnO2)·(1 MnO2) + (1 atom in H2O)·(2 H2O) = 4 | 4 = 4 ✓ |
| H: | (1 atom in H+)·(4 H+) = 4 | ⟶ | (2 atoms in H2O)·(2 H2O) = 4 | 4 = 4 ✓ |
| Charge: | 1·(-1) + 4·(+1) + 3·(-1) = 0 | ⟶ | 1·(0) + 2·(0) = 0 | 0 = 0 ✓ |
Collecting what we have so far:
| Oxidation: | Cr(OH)3(s) + H2O(l) | ⟶ | CrO42-(aq) + 5H+(aq) + 3e‾ |
| Reduction: | MnO4–(aq) + 4H+(aq) + 3e‾ | ⟶ | MnO2(s) + 2H2O(l) |
In this case, both half-reactions involve the same number of electrons, and therefore we can simply add the two half-reactions together and simplify:
| Cr(OH)3(s) + |
⟶ | CrO42-(aq) + |
| Cr(OH)3(s) + MnO4–(aq) | ⟶ | CrO42-(aq) + H+(aq) + MnO2(s) + H2O(l) |
This is the balanced redox equation in an acidic solution. To “convert” to basic solution, add OH−(aq) to both sides of the equation to “react” with all the H+(aq). This converts H+(aq) to H2O(l) on one side and adds OH−(aq) on the other side:
| Cr(OH)3(s) + MnO4–(aq) + OH−(aq) | ⟶ | CrO42-(aq) + H+(aq) + OH−(aq) + MnO2(s) + H2O(l) |
| Cr(OH)3(s) + MnO4–(aq) + OH−(aq) | ⟶ | CrO42-(aq) + MnO2(s) + 2H2O(l) |
This is the balanced equation in basic solution. Checking each side of the equation:
| Cr: | (1 atom in Cr(OH)3)·(1 Cr(OH)3) = 1 | ⟶ | (1 atom in CrO42-)·(1 CrO42-) = 1 | 1 = 1 ✓ |
| Mn: | (1 atom in MnO4–)·(1 MnO4–) = 1 | ⟶ | (1 atom in MnO2)·(1 MnO2) = 1 | 1 = 1 ✓ |
| O: | (3 in Cr(OH)3)·(1) + (4 in MnO4–)·(1) + (1 in OH–)·(1) = 8 | ⟶ | (4in CrO42-)·(1) + (2 in MnO2)·(1) + (1 in H2O)·(2) = 8 | 8 = 8 ✓ |
| H: | (3 in Cr(OH)3)·(1) + (1 in OH–)·(1) = 4 | ⟶ | (2 atoms in H2O)·(2 H2O) = 4 | 4 = 4 ✓ |
| Charge: | 1·(0) + 1·(-1) + 1·(-1) = -2 | ⟶ | 1·(-2) + 1·(0) + 2·(0) = -2 | -2 = -2 ✓ |
Exercise 5: Balancing Oxidation-Reduction Reactions
D38.4 Introduction to Voltaic Cells
A voltaic cell (or galvanic cell) is an electrochemical cell in which a spontaneous redox reaction produces an electric current. Consider what happens when a clean piece of copper metal is placed in a solution of silver nitrate.
When the copper metal contacts the silver nitrate solution, silver metal begins to form on the copper surface and Cu2+ ions pass into the solution (indicated by the blue-green color of the solution). The net ionic equation for the reaction is:
which may be split into its two half-reactions that sum to the overall reaction:
| Oxidation: | Cu(s) | ⟶ | Cu2+(aq) + 2 e‾ |
| Reduction: | 2 Ag+(aq) + 2 e‾ | ⟶ | 2 Ag(s) |
The half-reactions make clear that two electrons are transferred from a copper atom, which forms a Cu2+ ion. Each of the two electrons is then transferred to one Ag+ ion, which forms a silver atom. Because a flow of electrons constitutes an electric current, this electron transfer can generate an electric current if we devise a way to carry out the two half-reactions in separate vessels and connect them with a metal (electrically conductive) wire. This is in essence how a voltaic cell is designed. Figure 1 shows one way to do this.
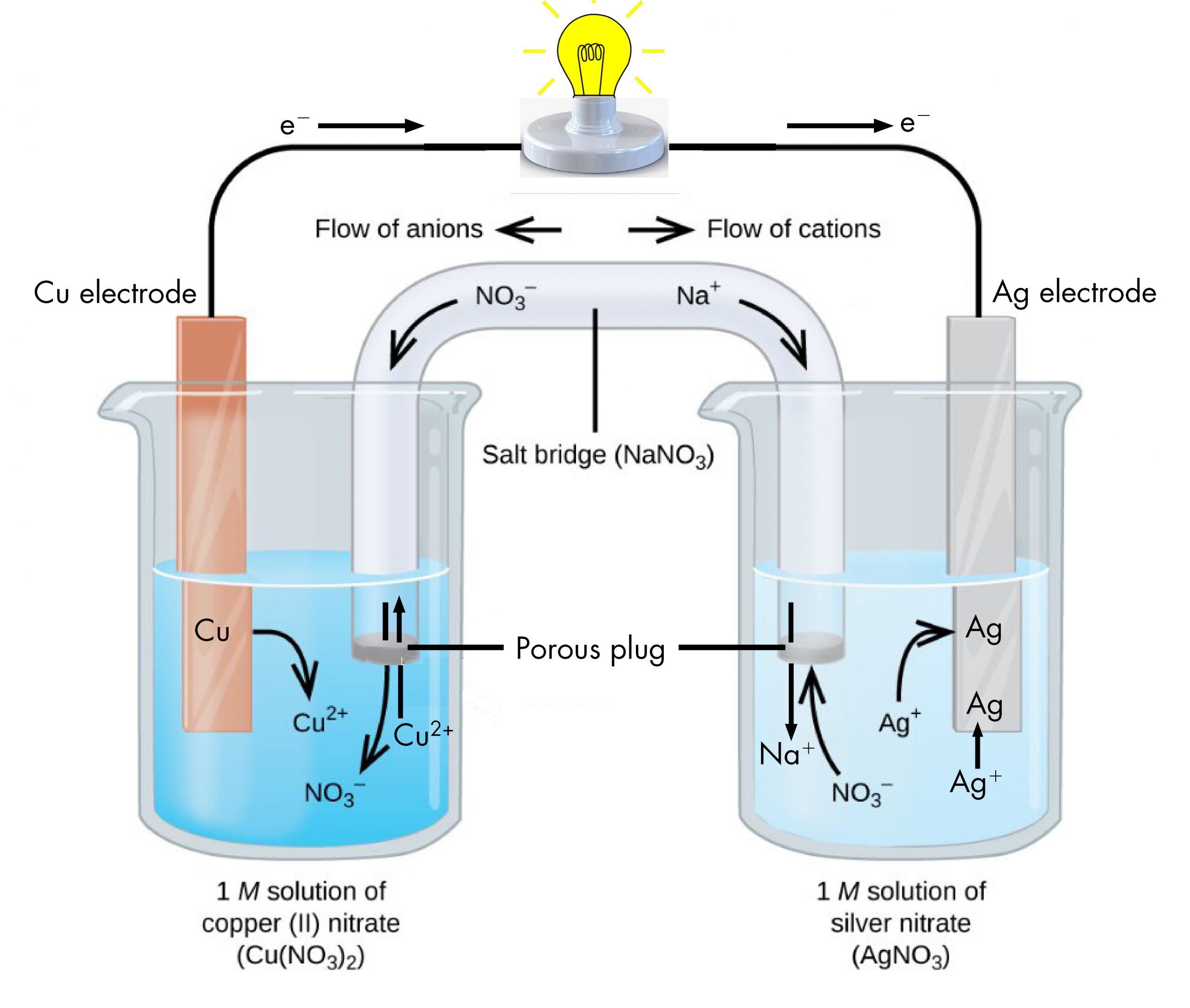
The beaker on the left contains a 1-M solution of copper(II) nitrate [Cu(NO3)2] with a strip of copper metal partially submerged in the solution. The copper strip is an electrode, a means for conducting electrons into or out of the solution. At the surface of the copper strip, the oxidation half-reaction occurs:
The flow of electrons (electric current) passes out of the solution via the copper strip, flows through the light bulb, and moves into the silver strip in the beaker on the right. In the right-hand beaker, the reduction half-reaction occurs near the surface of the silver strip:
Thus, with the two half-reactions occurring in separate beakers, an electric current can be generated. The container in which each half-reactions occurs is called a half-cell.
If this were all that happened, the electric current would not flow for long. In the left-hand beaker, one Cu2+ ion is added to the solution for every two electrons conducted into the external wire. This means that the solution is continuously accumulating excess positive ions as the reaction occurs and an electric charge is building up. Such a charge build up would prevent further oxidation reaction from occurring. This can be mitigated if some positive ions move out of the beaker or some negative ions move into the beaker. A similar issue is occurring in the right-hand beaker, where Ag+ ions are being removed from the solution. Balancing total ionic charges requires either negative ions move out of the right-hand solution or positive ions move in.
This balancing of ion charges in the two separated half-reactions is maintained by the salt bridge, a solution of a salt that does not mix with either half-cell solution but allows ions to pass into or out of the half-cells. By allowing ions to conduct charge into or out of the half-cells, the salt bridge completes the electrical circuit involving the two half-cells. Without it, current cannot flow for more than an instant. Notice that negative ions in the salt bridge move in the same direction as electrons around the circuit and positive ions move in the opposite direction.
The half-cell in which oxidation occurs is called the anode. The half-cell in which reduction occurs is called the cathode. It is easy to remember that the anode involves oxidation because both words begin with vowels. It is easy to remember that the cathode involves reduction because both words begin with consonants. These definitions, anode/oxidation and cathode/reduction, are true for any electrochemical cell, not just a voltaic cell.
Exercise 6: Reactions for a Voltaic Cell
Podia Question
Make a diagram of a voltaic cell that generates electric current from this product-favored chemical reaction:
Fe(s) + Cu(NO3)2(aq) → Fe(NO3)2(aq) + Cu(s)
Choose an appropriate salt solution for the salt bridge. Make sure that the oxidation half-reaction is in the left-hand beaker. Label each electrode with an element symbol. Label the anode half-cell and the cathode half-cell. Label the direction of movement of electrons, positive ions, and negative ions in the electrical circuit.
As this voltaic cell operates, one electrode gains mass and one electrode loses mass. Identify which electrode gains mass. Explain why that electrode gains mass and why the other electrode loses mass.
Two days before the next whole-class session, this Podia question will become live on Podia, where you can submit your answer.

