Unit One
Day 5: Ionic Compounds; Covalent Bonding
Applying Core Ideas: Two Substances, Some Similarities, Some Big Differences


Compare iron, which melts at 1811 K (1538 °C), and calcium fluoride, which melts at 1691 K (1418 °C). Are the forces between atomic-level particles similar in iron and calcium fluoride? Write in your notebook an explanation of your answer to this question.
Consider some other properties of iron and calcium fluoride.
Iron has typical metallic properties: pure solid iron has metallic luster, is malleable, and conducts electricity.
Calcium fluoride has significantly different properties: as a solid it is brittle, does not look metallic, and does not conduct electricity; when molten, calcium fluoride does conduct electricity though.
It appears that these two substances have similar attractions between atomic-level particles, but quite different properties. We need a better atomic-scale model to make sense of these differences.
D5.1 Ionic Compounds
In metals, which have low effective nuclear charges (and low ionization energies), it is relatively easy to form positive ions within a sea of electrons so that attractions among the ions and the electrons hold the atoms together. What happens when an atom with a low ionization energy interacts with an atom with a large negative electron affinity? In such a case, transfer of one or more electrons from the atom with the low ionization energy to the one with the high electron affinity can be energetically favorable. For example, consider transfer of an electron from a Li atom to a F atom to form a cation and anion close together: an ion pair, Li+F–.
From the activity above, you've worked out that the formation of the ion pair is associated with a negative ΔE: the joined ion pair is lower in total energy (more stable) than the two atoms from which it formed.
The gain and loss of electron(s) in forming an ion-pair typically results in a full octet for the cation and anion. For example:
When a large number of ions form, anions and cations form a structure, called an ionic crystal lattice, where there are equal numbers of anions and cations (so there is zero total electric charge); in the lattice each anion has several cations as its nearest neighbors, and each cation has several anions as its nearest neighbors (see example in Figure 1). This arrangement maximizes anion-cation attractions (smaller r results in lower Coulomb's law energy) and minimizes anion-anion and cation-cation repulsions (greater r between anions and between cations). A compound made up of anions and cations is called an ionic compound and the overall attraction making an ionic crystal lattice stable is called ionic bonding.
For example, when sodium cations (Na+) and bromide anions (Br−) come together, the crystal lattice of the compound sodium bromide, Figure 1, contains one Na+ (green) for each Br− (violet). The chemical formula representing the part of the lattice shown in Figure 1 is Na75Br75 because there are 75 Na+ and 75 Br− ions. The actual crystal is much larger so the subscripts in the formula of a real crystal would be huge. A formula unit is a group of chemical symbols that indicates the smallest whole number ratio of ions of each kind that make up the substance, and is typically used as the formula for ionic compounds. Thus, the formula unit (and the formula) for sodium bromide is NaBr.
All chemical substances are overall electrically neutral. Thus, in an ionic compound, the positive charge from all the cations must equal to the negative charge from all the anions. In other words, the subscripts in a formula unit of an ionic compound must result in equal quantities of positive and negative charges. If we know the charges of the ions, then we can write the formula.
Some ions consist of a group of atoms with an overall charge. Examples are sulfate dianion, SO42−, dihydrogen phosphate anion, H2PO4−, and ammonium cation, NH4+. It is quite useful to be able to recognize such polyatomic ions and their charges. If you need to refresh your knowledge of polyatomic ions, use the reference table as you do the next two exercises.
Exercise 1: Ionic Compounds with Polyatomic Ions
Exercise 2: Formulas for Ionic Compounds
D5.2 Lattice Energy
Refer back to Activity 1. The third step involved bringing one Li+ ion close to one F− ion, which lowered the energy. When a large number of oppositely charged ions are brought close together to form a crystal lattice (Figure 1), the energy is lowered even more, because more ions are close together in a structure where attractive forces predominate over repulsive forces.
The lattice energy of an ionic compound is defined as the decrease in energy when the ionic crystal lattice forms from the separated ions. Lattice energy can be calculated using a modified form of Coulomb's law; some calculated lattice energies are in Table 1. (Note that because lattice energy is defined as a decrease in energy, a large positive lattice energy corresponds to a large negative ΔE, that is, a very stable (low energy) ionic solid.)
| Substance | Lattice Energy (kJ/mol) | ||||||
|---|---|---|---|---|---|---|---|
| NaI | 682 | ||||||
| CaI2 | 1971 | ||||||
| MgI2 | 2293 | ||||||
| NaOH | 887 | ||||||
| Na2O | 2481 | ||||||
| NaNO3 | 755 | ||||||
| Ca3(PO4)2 | 10,602 | ||||||
| CaCO3 | 2804 | ||||||
| Table 1. Representative calculated lattice energies. Data from CRC Handbook of Chemistry and Physics (2004). | |||||||
Lattice energies have a wide range of values depending on which ions make up a compound. Consider, for example, why the lattice energy increases as you go from NaI, to CaI2, to MgI2 (first three rows in Table 1).
According to Coulomb's law, [latex]E_{\text{p}} = k_e\frac{Q_1Q_2}{r}[/latex], the lattice energy is directly proportional to the sizes of the charges on the ions and inversely proportional to the distance between them (the sum of their ionic radii). Thus, we can compare NaI, CaI2, and MgI2 with respect to magnitudes of charges and sizes of ions.
Magnitudes of Charges: NaI consists of 1+ ions and 1− ions; CaI2 and MgI2 consist of 2+ ions and 1− ions.
Because the magnitude of Q1Q2 is larger, the lattice energies of CaI2 and MgI2 should be larger than for NaI.
Sizes of ions: All three compounds contain I− anions, so we only need to compare cation radii.
The radii of Ca2+ and Na+ are similar. This can be estimated from the periodic table: Na+ and Ca2+ are both smaller than K+, Na+ because it is above K+ in the periodic table, and Ca2+ because it is isoelectronic with K+ but has more protons in the nucleus. It is reasonable to assume that the radii are not very different, and the ionic-radius table confirms this: Na+ 116 pm; Ca2+ 114 pm. Thus, r is not a major factor affecting lattice energy for NaI and CaI2.
The radius of Mg2+ is significantly smaller than for Ca2+ (and Na+) because Mg is directly above Ca in the periodic table and the ions have the same charge. Thus, MgI2 should have a larger lattice energy than CaI2, which is consistent with the values in the table.
When looking at Table 1, you may have noticed that lattice energies for compounds containing 2+ and 2− ions are nearly quadruple those for similar compounds containing 1+ and 1− ions of similar size (compare NaNO3 and CaCO3). This observation is consistent with the general rule that lattice energies are highest for substances with small, highly charged ions.
D5.3 Properties of Ionic Compounds
The physical and chemical properties of an ionic compound are determined by the ions that that constitute the compound. The compound's properties are quite different from the properties of the elements that reacted to form the compound. For example, both sodium and chlorine react with water, but sodium chloride (NaCl) dissolves in water without reacting. In other words, sodium ions and chloride ions do not react with water, but sodium atoms and Cl2 molecules do.
Ionic compounds have many physical properties in common:
- they usually have melting points and boiling points well above room temperature.
- they are crystalline solids with distinct crystal shapes
- they are brittle, will shatter if struck by a hammer, and can easily be cleaved (cleave means to break along smooth planes, as shown in this video).
- they are electrical insulators when solid but conduct electricity when molten (liquid). (See this video.)
- when an ionic compound dissolves in water, the solution conducts electricity much more effectively than pure water.
Because all ionic compounds have similar properties, it is useful to be able to identify an ionic compound from its chemical formula. In general, ionic compounds contain cations of metals from the left side of the periodic table and anions of nonmetals from the right side of the periodic table. If a compound’s chemical formula contains a polyatomic ion, then the compound is an ionic compound.
Exercise 3: Identifying Ionic Compounds
The properties of ionic compounds can be interpreted in terms of ions. In the solid phase, ions are essentially fixed in their positions in a crystal lattice. Lattice shapes depend on the number and type of ions in the formula, but each lattice has a distinctive shape that results in the lowest energy (maximum lattice energy). Because distances between ions are small, lattice energies are large. It requires a lot of energy to overcome attractions among the ions, making the crystal hard. The lattice shape is related to the shape of the macroscopic crystal. When a crystal cleaves, the cleavage planes are parallel to planes in the crystal lattice. (To see why, watch this video.)
When an ionic solid melts, the anions and cations are free to move randomly among each other. Although the average minimum distance between ions is still small (just a little larger than in the crystalline solid), some anions may be next to other anions and some cations near other cations. Hence, the electrostatic attractions are not as strong and the electrostatic repulsions are greater than in the solid phase; that is, part of the lattice energy needs to be overcome before an ionic compound melts.
When an ionic compound boils to form a gas, the ions continue to move randomly but also are so far apart that their electrostatic attractions are negligible. All of the lattice energy must be overcome for an ionic compound to boil.
Electric current is the movement of electric charge from one place to another. Electric charge is carried by any moving charged particle. In a liquid ionic compound, where ions can move independently, electric charge is conducted by ions. When a solid ionic compound dissolves in water, the ions separate and can move independently throughout the solution. Movement of ions conducts electricity through the solution, just as it does in the molten liquid.
Applying Core Ideas: Comparing Hydrogen Atoms and Helium Atoms
The boiling point of helium is 4.22 K (−268.93 °C), a consequence of very weak London dispersion forces (LDFs) between He atoms. Even when two He atoms are only a short distance apart, there is very little attraction.
When two H atoms get close there is a much stronger attraction: the two atoms become a H2 molecule by forming a covalent chemical bond. For the H2 molecules to have enough energy to break that bond, separating the two H atoms, the temperature needs to be similar to the temperature of the Sun (5778 K)!
Why do He atoms behave so differently from H atoms? We need to refine our models of structure and energy still further. This is done in the next sections.
D5.4 Covalent Bonding: Molecular Orbitals
Activity 6: Covalent Chemical Bonds
If you wrote that a covalent bond involves sharing electrons between atoms, that's a good start. But how does sharing electrons hold atoms together?
Just as a balance of Coulomb's-law attractions and repulsions affects the electron(s) and nucleus in an atom, coulombic interactions affect electrons and nuclei in a molecule. The major difference is that in a molecule, each electron interacts with two or more nuclei; this additional interaction provides the stabilization that allows the molecule to exist. If a collection of separate atoms were more stable than a molecule, the molecule would simply fall apart into individual atoms.
Just as electron(s) occupy stable atomic orbitals around a single nucleus in an atom, electrons occupy stable orbitals around multiple nuclei in a molecule. An orbital that extends over two or more atomic nuclei is called a molecular orbital (MO); in the MO model, a molecular orbital forms when atomic orbitals (AOs) overlap (or interpenetrate).
To understand this better, think about the formation of a H2 molecule from two ground-state hydrogen atoms (labeled as HA and HB in Figure 3) . When HA is sufficiently far away from HB—for example, more than 400 pm apart (top of Figure 3)—its electron (eA) occupies the lowest-energy atomic orbital, the 1s orbital. The same is true for HB.
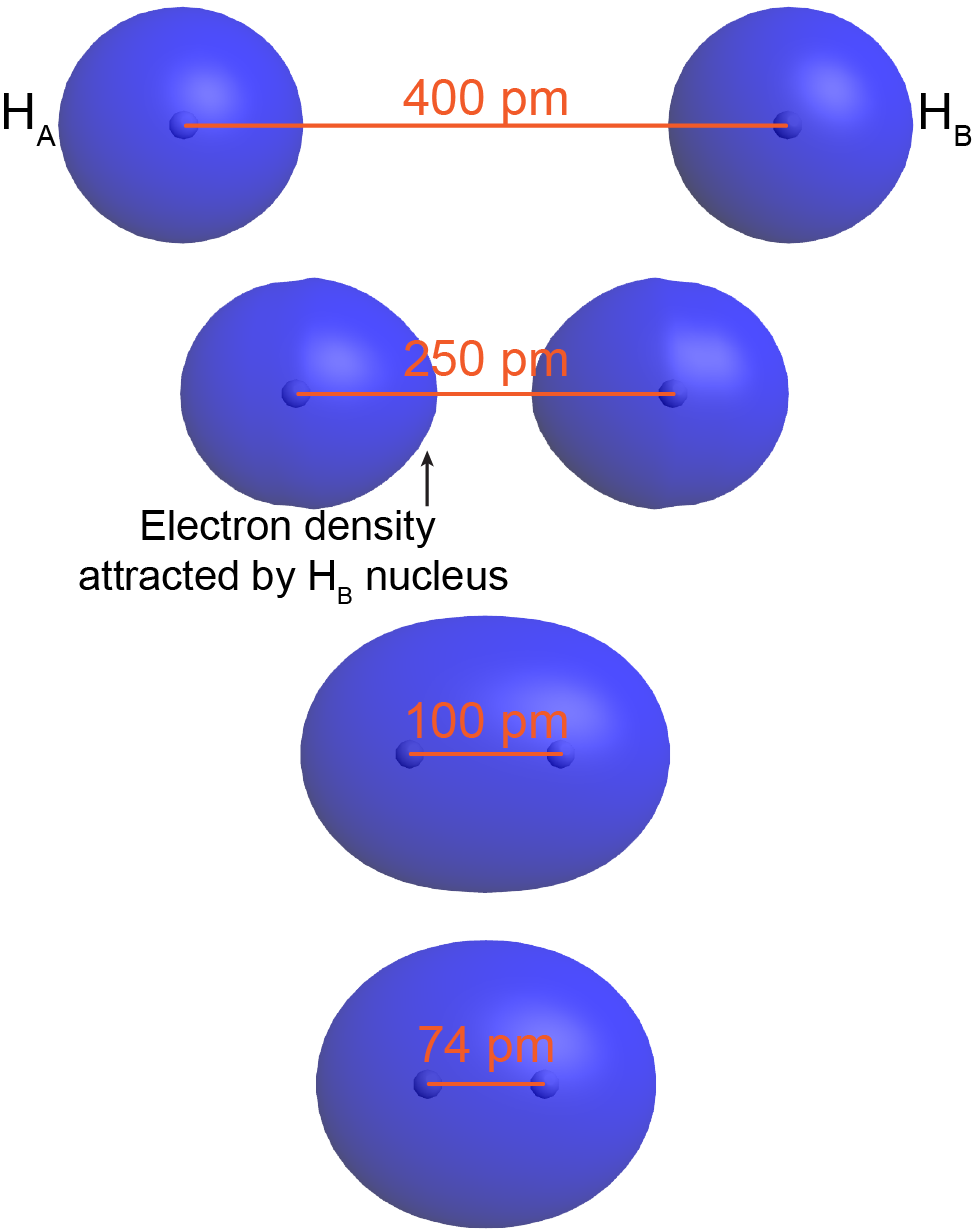
When HA and HB are closer, eA begins to experience significant Coulomb's-law attraction towards HB's nucleus. For example, at 250 pm apart (Figure 3, second from top) the orbital occupied by eA is no longer spherical around HA's nucleus but rather is distorted—there is more electron density on the side toward HB. Although HA's nucleus attracts eA more strongly than HB's nucleus does (because HB's nucleus is screened by eB), there is a net increase in the positive charge interacting with eA. This lowers eA's potential energy. The same argument applies to eB.
When the two atoms are even closer—for example, 100 pm apart—eA and eB become delocalized over both nuclei: both electrons occupy a molecular orbital, which surrounds both nuclei. Notice that in this H2 molecular orbital, there is significant electron density in between the two nuclei, attracting both nuclei. This lowers the overall energy relative to the energy of the two separate hydrogen atoms.
As the two atoms get closer still, there is a minimum in the overall energy for the molecule. For H2 the minimum is at 74 pm (bottom of Figure 3). At internuclear distances smaller than 0.74 Å, the energy rises again due to increasing nucleus-nucleus repulsion. In a ground-state H2 molecule the distance between nuclei of two bonded atoms, the bond length, is 74 pm.
Figure 4 allows you to explore how the electron density changes as two H atoms interact to form H2 (or how an H2 molecule dissociates into two separate H atoms). The blue dot on the potential energy curve shows the corresponding internuclear distance (bond length) and potential energy of the molecule. The ground-state H2 molecule is more stable than the two separated ground-state H atoms. (The energy of the separated atoms is set to be 0 kJ/mol in Figure 4.) The magnitude of the energy reduction, 436 kJ/mol, is called the bond energy, the energy required to break the bond, completely separating the atoms.
What we have just described is one of two ways that the two H 1s atomic orbitals can overlap/combine to form an H2 molecular orbital. It occurs when the two 1s atomic orbitals are in-phase. In-phase means that wave functions describing electrons A and B both have maxima in the same direction at the same time.
The second possibility is that the two overlapping 1s atomic orbitals are out-of-phase, which means that one atomic wave function is positive and the other atomic wave function is negative. This is shown in Figure 5, where the two phases (positive and negative) are shown in green and yellow.

The result is a molecular orbital with a node halfway between the two H atoms. (The node, where electron density is zero, is a plane perpendicular to a line connecting the two nuclei, the internuclear axis). Note that the bottom depiction in Figure 5 is a single molecular orbital with one node, just as the bottom depiction in Figure 3 is a single molecular orbital but without a node.
As is true of atomic orbitals, a molecular orbital with more nodes has higher energy, which makes sense because the presence of the node reduces electron density between the nuclei (compared to the electron densities of the individual atoms). This reduction in electron density results in less electron-nucleus attraction than if the atomic orbitals had not interacted at all.
D5.5 Molecular Orbital (MO) Diagram
When two H atoms come together to form H2, both in-phase overlap and out-of-phase overlap of 1s atomic orbitals are possible and both occur. Hence, two 1s atomic orbitals (AOs) overlap to form two molecular orbitals (MOs). This is true in general: the number of MOs formed equals the total number of AOs from which they are derived.
A MO diagram shows the relative energies of MOs and AOs and indicates which MOs form from overlap of which AOs. For example, Figure 6 shows the MO diagram of the H2 molecule. A MO lower in energy than the AOs from which it is derived is called a bonding MO. An electron occupying this bonding MO increases the stability of the bond (strengthens the bond). The H2 bonding MO is labeled "σ1s"; the subscript "1s" designates that it is derived from the 1s AOs.
A MO higher in energy than the AOs from which it is derived is called an antibonding MO—an electron occupying this MO decreases the stability of the bond (weakens the bond). The H2 antibonding MO is labeled as "[latex]\sigma^*_{1s}[/latex]."; the "*" denotes that it is an antibonding MO.
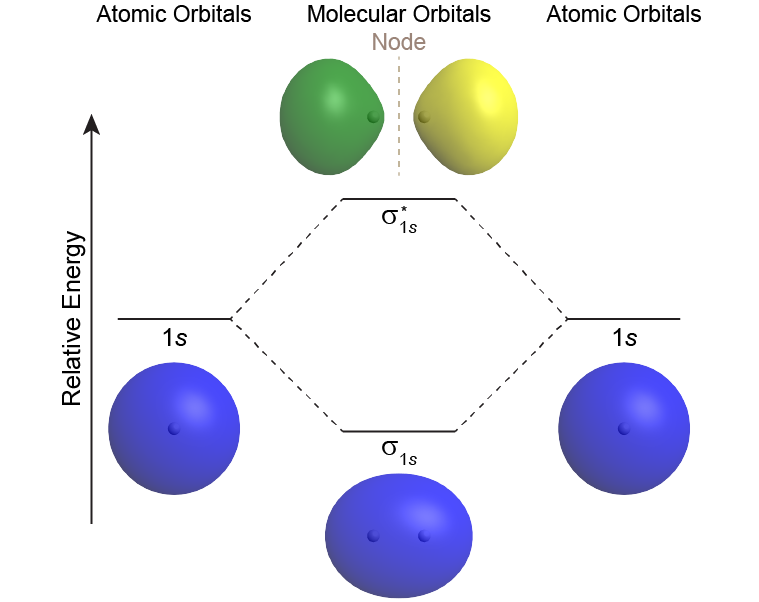
The Greek letter in the MO labels denotes the symmetry of the MO with respect to the internuclear axis (the line connecting the two nuclei). Greek letters σ, π, δ are analogous to the Roman letters s, p, d that designate shapes of atomic orbitals. A MO that is cylindrically symmetric is called a sigma MO and designated σ. (Cylindrically symmetric means that if you stood the molecule on end and spun it around the internuclear axis it would look the same all the time—just as a cylinder would look if you stood it on end and spun it).
Chemists often use simple 2D drawings to show both the shape and phase of AOs and MOs. So the sphere of a 1s AO is drawn as a circle and its phase is indicated by two different colors or shading/no shading or plus/minus sign. For example, formation of the σ1s MO from two 1s AOs can be drawn as:

where the black dots represent H nuclei, the circles with hatching (or + sign) represent boundary-surface plots of H 1s AOs, each with positive phase, and the oval with hatching (or + sign) represents the H2 σ1s MO, also with positive phase.
Exercise 4: Molecular Orbital Formation
D5.6 Electron Configurations and Bond Order
Just as an atom has an electron configuration, so does a molecule. The molecular ground-state electron configuration can be obtained by filling MOs, facilitated by MO diagrams such as the one shown in Figure 6, following rules similar to those for atomic electron configurations:
- Sum all the electrons from all the atoms that make up the molecule.
- Each MO can hold at most two electrons. (Two electrons occupying the same orbital must have opposite spin.)
- In the MO diagram the MOs are arranged in order of increasing energy.
- Add electrons to the lowest-energy MO first and then to successively higher-energy MOs (Aufbau principle)
- If two or more MOs have the same energy (are degenerate), apply Hund's rule: assign one electron to each degenerate MO before pairing any electrons
For the H2 molecule: there is one electron from each H atom, so there are two electrons in H2. There is only one lowest-energy MO, σ1s, therefore the two electrons, with opposite spin, will fill it. The ground state electron configuration of H2 is (σ1s)2.
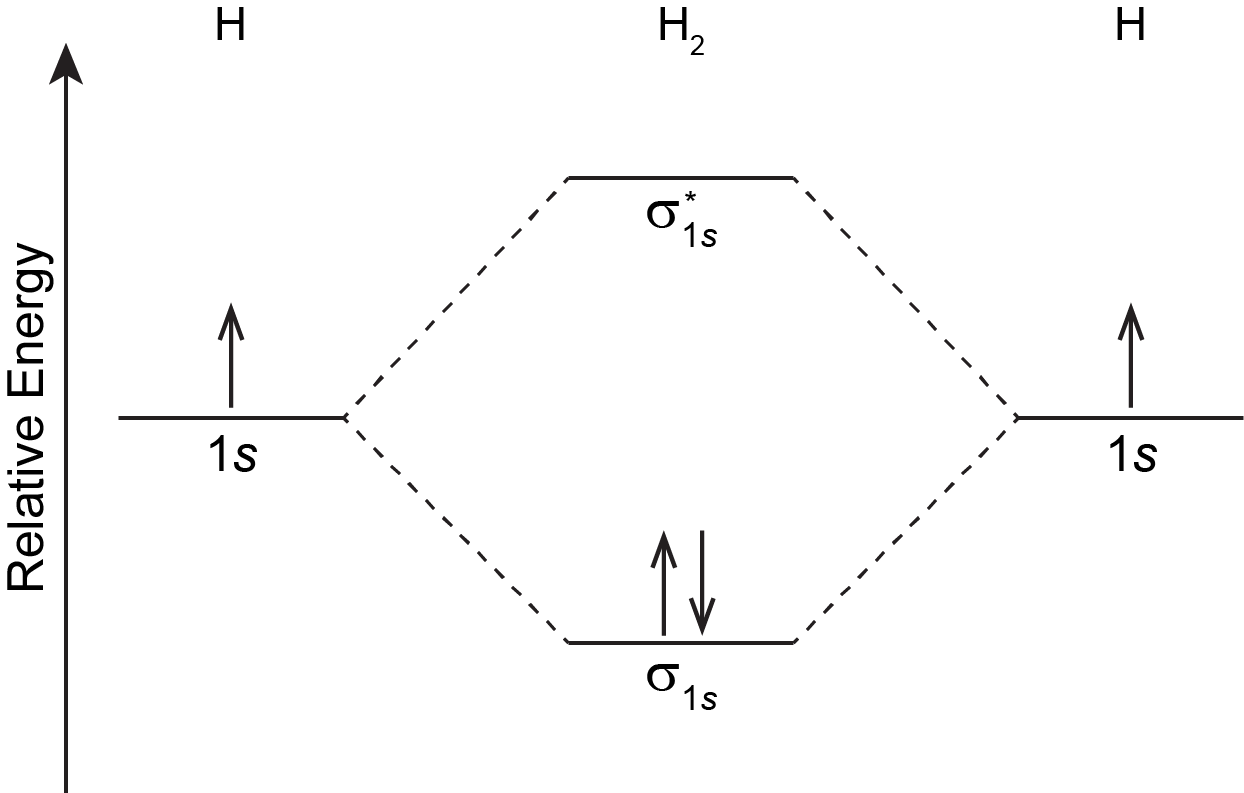
In Figure 6 in the previous section, and by convention in general, phases for occupied MOs are indicated by blue and red (when needed), while phases for unoccupied MOs are indicated by green and yellow. That is, [latex]\sigma_{1s}[/latex] is blue because it has two electrons and is all the same phase; [latex]\sigma^*_{1s}[/latex] is green and yellow because there are no electrons in this MO and one part is opposite phase from the other.
Activity 7: Molecular Orbitals and Electromagnetic Radiation
The two electrons in the σ1s MO, which are shared between the two H atoms, form a covalent bond. The configuration (σ1s)2 indicates a single, sigma covalent bond. In general, a covalent bond involves overlap of two or more AOs that leads to increased electron densities close to atomic nuclei so that the electrons' energies are lowered. Electrons are shared between pairs of atomic nuclei, or more widely among several nuclei within a molecule.
In some cases more than two electrons can be shared between two nuclei. This gives rise to the idea of bond order, which is the number of shared electron pairs between two atoms. Using a MO diagram, bond order can be defined as:
where nbonding e‾ is the number of electrons in bonding MOs and nantibonding e‾ is the number of electrons in antibonding MOs. There is a factor [latex]\frac{1}{2}[/latex] because two shared electrons make one bond. In general a greater number of shared electrons means a stronger bond, so the larger the bond order is, the stronger the bond is.
Exercise 5: Bond Order
Activity 8: Molecular Orbitals for He2
This Podia problem is based on today's pre-class material; working through that material will help you solve the problem.
The formulas and melting points of four salts are listed below. All four compounds have the same crystal lattice as NaCl. Write a clear, concise explanation of the differences in melting points using scientifically appropriate language and including any relevant data.
NaF 996 °C NaCl 801 °C KCl 770 °C CaO 2572 °C
Two days before the next whole-class session, this Podia question will become live on Podia, where you can submit your answer.

