Additional Reading Materials
Chapter 15: Acid and Base Reactions
Ch15.1 Brønsted-Lowry Acids and Bases
Acids and bases have been known for a long time. When Robert Boyle characterized them in 1680, he noted that acids dissolve many substances, change the color of certain natural dyes (for example, they change litmus from blue to red), and lose these characteristic properties after coming into contact with alkalis (bases). In the eighteenth century, it was recognized that acids have a sour taste, react with limestone to liberate a gaseous substance (now known to be CO2), and interact with alkalis to form neutral substances. In 1815, Humphry Davy contributed greatly to the development of the modern acid-base concept by demonstrating that hydrogen is the essential constituent of acids. Around that same time, Joseph Louis Gay-Lussac concluded that acids are substances that can neutralize bases and that these two classes of substances can be defined only in terms of each other. The significance of hydrogen was reemphasized in 1884 when Carl Axel Arrhenius defined an acid as a compound that dissolves in water to yield hydrogen cations (now recognized to be hydronium ions, H3O+) and a base as a compound that dissolves in water to yield hydroxide anions (OH−). This definition is not wrong; it is simply limited.
A more general definition was proposed in 1923 by the Danish chemist Johannes Brønsted and the English chemist Thomas Lowry. Their definition centers on the proton, H+. A proton is what remains when a normal hydrogen atom loses an electron. A compound that donates a proton to another compound is called a Brønsted-Lowry acid, and a compound that accepts a proton is called a Brønsted-Lowry base. An acid-base reaction is the transfer of a proton from a proton donor (acid) to a proton acceptor (base). Although we will not discuss it much in this course, there is an even more general model of acid-base behavior introduced by the American chemist G. N. Lewis, in which acids and bases are identified by their ability to accept or to donate a pair of electrons instead.
Acids may be compounds such as HCl or H2SO4, organic acids like acetic acid (CH3COOH) or ascorbic acid (vitamin C), or H2O. Anions (such as HSO4–, H2PO4–, HS–, and HCO3–) and cations (such as H3O+, NH4+, and [Al(H2O)6]3+) may also act as acids. Bases fall into the same three categories. Bases may be neutral molecules (such as H2O, NH3, and CH3NH2), anions (such as OH–, HS–, HCO3–, CO32-, F–, and PO43-), or cations (such as [Al(H2O)5OH]2+). The most familiar bases are ionic compounds such as NaOH and Ca(OH)2, which contain the hydroxide ion, OH−. The hydroxide ion in these compounds accepts a proton from acids to form water:
We call the product that remains after an acid donates a proton the conjugate base of that acid. This species is a base because it can accept a proton, thereby re-forming the acid:
We call the product that results when a base accepts a proton that base’s conjugate acid. This species is an acid because it can give up a proton and thus re-form the base:
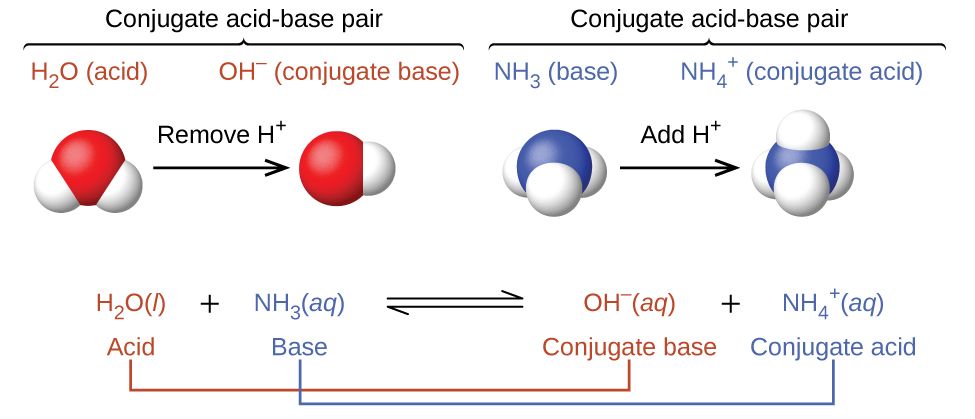
In the above reaction equations, the behaviors of acids as proton donors and bases as proton acceptors are represented in isolation. In reality, all acid-base reactions involve the transfer of protons between acids and bases. For example, consider the acid-base reaction that takes place when ammonia is dissolved in water. A water molecule (functioning as an acid) transfers a proton to an ammonia molecule (functioning as a base), yielding the conjugate base of water, OH−, and the conjugate acid of ammonia, NH4+:
The reaction between a Brønsted-Lowry acid and water is called acid ionization. For example, when hydrogen fluoride dissolves in water and ionizes, protons are transferred from HF molecules to water molecules, yielding hydronium ions and fluoride ions:

When we add a base to water, a base ionization reaction occurs in which protons are transferred from water molecules to base molecules. For example, adding pyridine to water yields hydroxide ions and pyridinium ions:
![This figure has two rows. In both rows, a chemical reaction is shown. In the first, structural formulas are provided. In this model, in red, is an O atom which has H atoms singly bonded above and to the right. The O atom has lone pairs of electron dots on its left and lower sides. This is followed by a plus sign. The plus sign is followed, in blue, by an N atom with one lone pair of electron dots. The N atom forms a double bond with a C atom, which forms a single bond with a C atom. The second C atom forms a double bond with another C atom, which forms a single bond with another C atom. The fourth C atom forms a double bond with a fifth C atom, which forms a single bond with the N atom. This creates a ring structure. Each C atom is also bonded to an H atom. An equilibrium arrow follows this structure. To the right, in brackets is a structure where an N atom bonded to an H atom, which is red, appears. The N atom forms a double bond with a C atom, which forms a single bond with a C atom. The second C atom forms a double bond with another C atom, which forms a single bond with another C atom. The fourth C atom forms a double bond with a fifth C atom, which forms a single bond with the N atom. This creates a ring structure. Each C atom is also bonded to an H atom. Outside the brackets, to the right, is a superscript positive sign. This structure is followed by a plus sign. Another structure that appears in brackets also appears. An O atom with three lone pairs of electron dots is bonded to an H atom. There is a superscript negative sign outside the brackets. To the right, is the equation: k equals [ C subscript 5 N H subscript 6 superscript positive sign ] [ O H superscript negative sign] all divided by [ C subscript 5 N H subscript 5 ]. Under the initial equation, is this equation: H subscript 2 plus C subscript 5 N H subscript 5 equilibrium arrow C subscript 5 N H subscript 6 superscript positive sign plus O H superscript negative sign. H subscript 2 O is labeled, “acid,” in red. C subscript 5 N H subscript 5 is labeled, “base,” in blue. C subscript 5 N H subscript 6 superscript positive sign is labeled, “acid” in blue. O H superscript negative sign is labeled, “base,” in red.](https://wisc.pb.unizin.org/app/uploads/sites/126/2017/08/CNX_Chem_14_01_NH3_img.jpg)
Notice that both these ionization reactions are represented as equilibrium processes. The relative extent to which these acid and base ionization reactions proceed is an important topic in a later section.
Ch15.2 Autoionization of Water
In the two above examples, we also saw that water can function as either an acid or a base, depending on the nature of the solute dissolved in it. In fact, in pure water or in any aqueous solution, water acts both as an acid and a base. A very small fraction of water molecules donate protons to other water molecules to form hydronium ions and hydroxide ions:
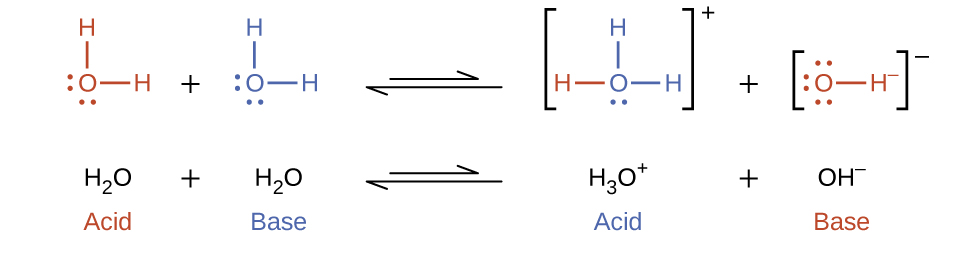
This type of reaction, in which a substance ionizes when one molecule of the substance reacts with another molecule of the same substance, is referred to as autoionization.
Pure water undergoes autoionization to a very slight extent. Only about two out of every 109 molecules in a sample of pure water are ionized at 25 °C. The equilibrium constant for the ionization of water is called the ionization constant for water (Kw):
The slight ionization of pure water is reflected in the small value of the equilibrium constant; at 25 °C, Kw has a value of 1.0 × 10−14. The process is endothermic, and so the extent of ionization and the resulting concentrations of hydronium ion and hydroxide ion increase with temperature. For example, at 100 °C, the value for Kw is about 5.6 × 10−13, roughly 50 times larger than the value at 25 °C.
Example 1
Ion Concentrations in Pure Water
What are the H3O+ concentration and the OH– concentration in pure water at 25 °C?
Solution
The autoionization of water yields the same number of hydronium and hydroxide ions. Therefore, in pure water, [H3O+] = [OH−]. At 25 °C:
So:
The hydronium ion concentration and the hydroxide ion concentration are the same, and we find that both equal 1.0 × 10−7M.
Check Your Learning
At 80 °C is Kw = 2.4 × 10−13. What are the concentrations of hydronium and hydroxide ions in pure water at 80 °C?
Answer:
[H3O+] = [OH−] = 4.9 × 10−7M
It is important to realize that the autoionization equilibrium for water is established in all aqueous solutions. Adding an acid or base to water will not change the position of the equilibrium. Example 2 demonstrates the quantitative aspects of this relation between hydronium and hydroxide ion concentrations.
Example 2
The Inverse Proportionality of [H3O+] and [OH−]
A solution of carbon dioxide in water has [H3O+] = 2.0 × 10−6M. What is the concentration of OH– at 25 °C?
Solution
We know the value of the ion-product constant for water at 25 °C:
Thus, we can calculate the missing equilibrium concentration.
Rearrangement of the Kw expression yields:
The hydroxide ion concentration is reduced to 5.0 × 10−9M as the hydronium ion concentration increases to 2.0 × 10−6M. This is expected from Le Châtelier’s principle: the autoionization reaction shifts to the left to reduce the stress of the increased hydronium ion concentration and the [OH−] is reduced relative to that in pure water.
A check of these concentrations confirms that our arithmetic is correct:
Check Your Learning
What is the hydronium ion concentration in an aqueous solution with a hydroxide ion concentration of 0.001 M at 25 °C?
Answer:
[H3O+] = 1 × 10−11M
Ch15.3 Amphiprotic Species
Like water, many molecules and ions may either gain or lose a proton under the appropriate conditions. Such species are said to be amphiprotic. Another term used to describe such species is amphoteric, which is a more general term for a species that may act either as an acid or a base by any definition (not just the Brønsted-Lowry one). Consider for example the bicarbonate ion, which may either donate or accept a proton as shown here:
Example 3
Representing the Acid-Base Behavior of an Amphoteric Substance
Write separate equations representing the reaction of HSO3–
(a) as an acid with OH−
(b) as a base with HI
Solution
(a) [latex]\text{HSO}_3^{\;\;-}(aq)\;+\;\text{OH}^{-}(aq)\;{\leftrightharpoons}\;\text{SO}_3^{\;\;2-}(aq)\;+\;\text{H}_2\text{O}(l)[/latex]
(b) [latex]\text{HSO}_3^{\;\;-}(aq)\;+\;\text{HI}(aq)\;{\leftrightharpoons}\;\text{H}_2\text{SO}_3(aq)\;+\;\text{I}^{-}(aq)[/latex]
Check Your Learning
Write separate equations representing the reaction of H2PO4–
(a) as a base with HBr
(b) as an acid with OH−
Answer:
(a) [latex]\text{H}_2\text{PO}_4^{\;\;-}(aq)\;+\;\text{HBr}(aq)\;{\leftrightharpoons}\;\text{H}_3\text{PO}_4(aq)\;+\;\text{Br}^{-}(aq)[/latex];
(b) [latex]\text{H}_2\text{PO}_4^{\;\;-}(aq)\;+\;\text{OH}^{-}(aq)\;{\leftrightharpoons}\;\text{HPO}_4^{\;\;2-}(aq)\;+\;\text{H}_2\text{O}(l)[/latex]
Ch15.4 pH and pOH
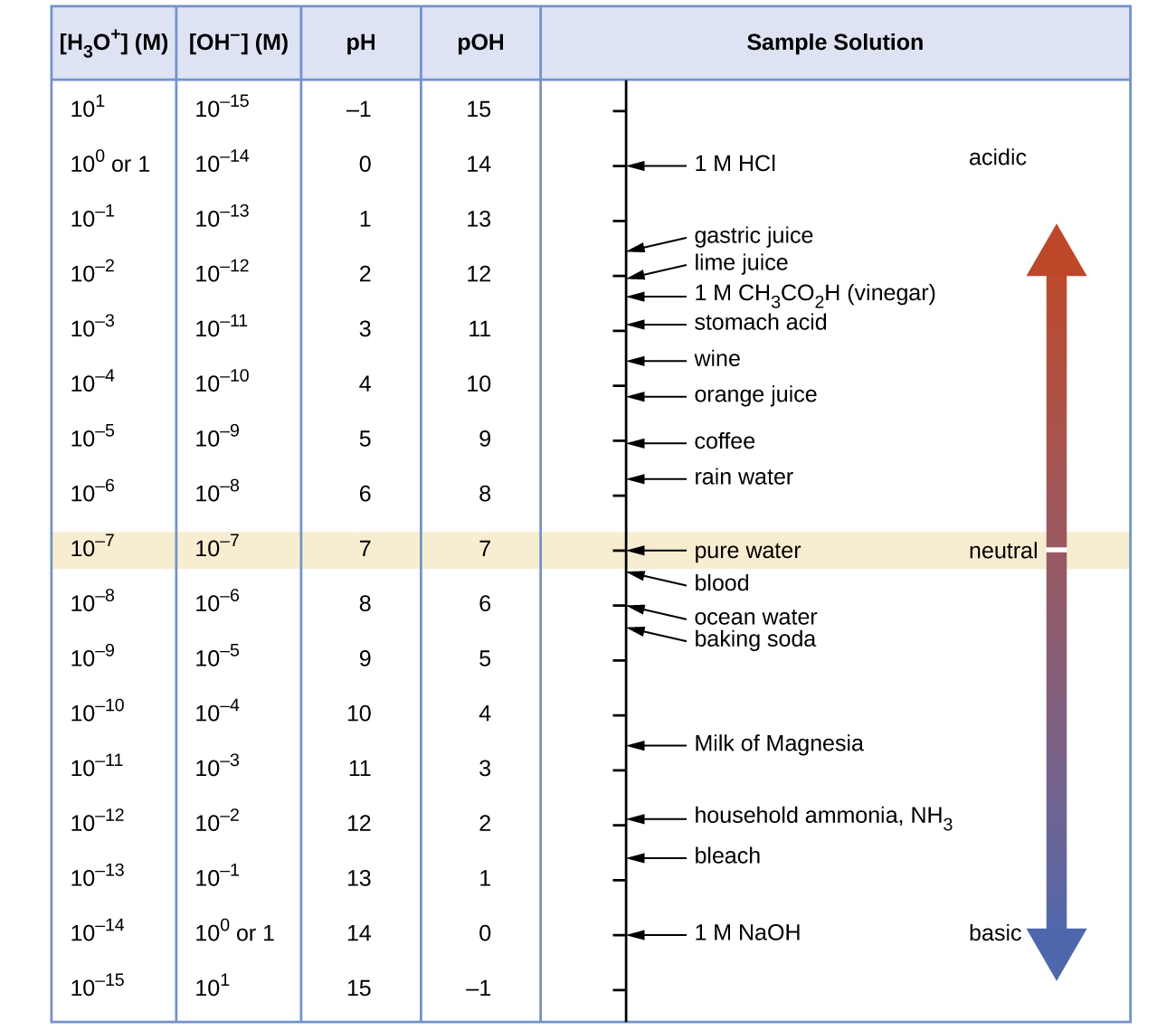
The concentrations of hydronium and hydroxide ions in a solution are often critical determinants of the solution’s properties and the chemical behaviors of its other solutes, and specific vocabulary has been developed to describe these concentrations in relative terms. A solution is neutral if it contains equal concentrations of hydronium and hydroxide ions; acidic if it contains a greater concentration of hydronium ions than hydroxide ions; and basic if it contains a lesser concentration of hydronium ions than hydroxide ions.
A common means of expressing values that may span many orders of magnitude is to use a logarithmic scale. One such scale that is very popular for chemical concentrations and equilibrium constants is based on the p-function:
where “X” is the quantity of interest and “log” is the base-10 logarithm. The pH of a solution is therefore defined as:
Rearranging this equation to isolate the hydronium ion molar concentration yields the equivalent expression:
Likewise, the hydroxide ion molarity may be expressed as pOH:
Finally, the relation between pH and pOH is easily derived from the Kw expression:
At 25 °C, the value of Kw is 1.0 × 10−14, and so:
The pH and pOH of a neutral solution at this temperature are therefore:
Therefore, at this temperature, acidic solutions are those with [H3O+] > 1.0 × 10−7M and [OH–] < 1.0 × 10−7M (corresponding to pH < 7.00 and pOH > 7.00). Basic solutions are those with [H3O+] < 1.0 × 10−7M and [OH–] > 1.0 × 10−7M (corresponding to pH > 7.00 and pOH < 7.00).
Since the autoionization constant Kw is temperature dependent, these correlations between pH values and the acidic/neutral/basic adjectives will be different at temperatures other than 25 °C. For example, the hydronium molarity of pure water at 80 °C is 4.9 × 10−7M, which corresponds to pH and pOH values of:
At this temperature, then, neutral solutions exhibit pH = pOH = 6.31, acidic solutions exhibit pH < 6.31 and pOH > 6.31, whereas basic solutions exhibit pH > 6.31 and pOH < 6.31. This distinction can be important when studying certain processes that occur at nonstandard temperatures, such as enzyme reactions in warm-blooded organisms. Unless otherwise noted, references to pH values are presumed to be those at standard temperature (25 °C) (Table 1).
| Classification | Relative Ion Concentrations | pH at 25 °C |
|---|---|---|
| acidic | [H3O+] > [OH−] | pH < 7 |
| neutral | [H3O+] = [OH−] | pH = 7 |
| basic | [H3O+] < [OH−] | pH > 7 |
| Table 1. Summary of Relations for Acidic, Basic and Neutral Solutions | ||
Figure 1 shows the relationships between [H3O+], [OH−], pH, and pOH, and gives values for these properties at standard temperatures for some common substances.
Example 4
Calculation of pH from [H3O+]
What is the pH of stomach acid, a solution of HCl with a hydronium ion concentration of 1.2 × 10−3M?
Solution
(When taking the log of a value, keep as many decimal places in the result as there are significant figures in the value.)
Check Your Learning
Water exposed to air contains carbonic acid, H2CO3, due to the reaction between carbon dioxide and water:
Air-saturated water has a hydronium ion concentration caused by the dissolved CO2 of 2.0 × 10−6M, about 20-times larger than that of pure water. Calculate the pH of the solution at 25 °C.
Answer:
5.70
Example 5
Calculation of Hydronium Ion Concentration from pH
Calculate the hydronium ion concentration of blood, the pH of which is 7.3 (slightly alkaline).
Solution
(On a calculator take the antilog, or the “inverse” log, of −7.3, or calculate 10−7.3.)
Check Your Learning
Calculate the hydronium ion concentration of a solution with a pH of −1.07.
Answer:
12 M
Environmental Science
Normal rainwater has a pH between 5 and 6 due to the presence of dissolved CO2 which forms carbonic acid:
Acid rain is rainwater that has a pH of less than 5, due to a variety of nonmetal oxides, including CO2, SO2, SO3, NO, and NO2 being dissolved in the water and reacting with it to form not only carbonic acid, but sulfuric acid and nitric acid. The formation and subsequent ionization of sulfuric acid are shown here:
Carbon dioxide is naturally present in the atmosphere because we and most other organisms produce it as a waste product of metabolism. Carbon dioxide is also formed when fires release carbon stored in vegetation or when we burn wood or fossil fuels. Sulfur trioxide in the atmosphere is naturally produced by volcanic activity, but it also stems from burning fossil fuels, which have traces of sulfur, and from the process of “roasting” ores of metal sulfides in metal-refining processes. Oxides of nitrogen are formed in internal combustion engines where the high temperatures make it possible for the nitrogen and oxygen in air to chemically combine.
Acid rain is a particular problem in industrial areas where the products of combustion and smelting are released into the air without being stripped of sulfur and nitrogen oxides. In North America and Europe until the 1980s, it was responsible for the destruction of forests and freshwater lakes, when the acidity of the rain actually killed trees, damaged soil, and made lakes uninhabitable for all but the most acid-tolerant species. Acid rain also corrodes statuary and building facades that are made of marble and limestone (Figure 2). Regulations limiting the amount of sulfur and nitrogen oxides that can be released into the atmosphere by industry and automobiles have reduced the severity of acid damage to both natural and manmade environments in North America and Europe. It is now a growing problem in industrial areas of China and India.
For further information on acid rain, visit this website hosted by the US Environmental Protection Agency.

Example 6
Calculation of pOH
What are the pOH and the pH of a 0.0125-M solution of potassium hydroxide, KOH?
Solution
Potassium hydroxide is a highly soluble ionic compound and completely dissociates when dissolved in dilute solution, yielding [OH−] = 0.0125 M:
The pH can be found from the pOH:
Check Your Learning
The hydronium ion concentration of vinegar is approximately 4 × 10−3M. What are the corresponding values of pOH and pH?
Answer:
pOH = 11.6, pH = 2.4
The acidity of a solution is typically assessed experimentally by measurement of its pH. The pOH of a solution is not usually measured, as it is easily calculated from an experimentally determined pH value. The pH of a solution can be directly measured using a pH meter (Figure 3).

The pH of a solution may also be visually estimated using colored indicators (Figure 4).

Ch15.5 Relative Strength of Acids and Bases
We can rank the strengths of acids by the extent to which they ionize in aqueous solution. The reaction of an acid with water is given by the general expression:
Water is the base that reacts with the acid HA, A− is the conjugate base of the acid HA, and the hydronium ion is the conjugate acid of water. A strong acid yields 100% (or very nearly so) of H3O+ and A− when the acid ionizes in water; Figure 5 lists several strong acids. A weak acid gives small amounts of H3O+ and A−.
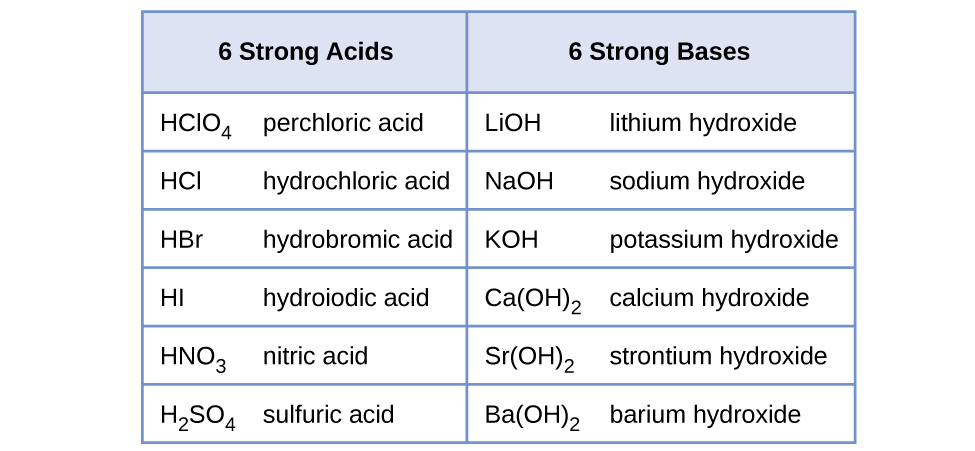
The relative strengths of acids may be determined by measuring their equilibrium constants in aqueous solutions. In solutions of the same concentration, stronger acids ionize to a greater extent, and so yield higher concentrations of hydronium ions than do weaker acids. The equilibrium constant for an acid is called the acid-ionization constant, Ka. For the reaction of an acid HA:
we write the equation for the ionization constant as:
where the concentrations are those at equilibrium. Although water is a reactant in the reaction, it is the solvent as well, so we do not include [H2O] in the equation. The larger the Ka of an acid, the larger the concentration of H3O+ and A− relative to the concentration of the nonionized acid, HA. Thus a stronger acid has a larger ionization constant than does a weaker acid.
For example, the following data on acid-ionization constants indicate the order of acid strength:
We can rank the strengths of bases by their tendency to form hydroxide ions in aqueous solution. The reaction of a Brønsted-Lowry base with water is given by:
Water is the acid that reacts with the base, HB+ is the conjugate acid of the base B, and the hydroxide ion is the conjugate base of water. As we did with acids, we can measure the relative strengths of bases by measuring their base-ionization constant (Kb) in aqueous solutions. We write the equation for the ionization constant as:
where the concentrations are those at equilibrium.
In solutions of the same concentration, stronger bases ionize to a greater extent, and so yield higher hydroxide ion concentrations than do weaker bases. A stronger base has a larger ionization constant than does a weaker base. Figure 5 lists several strong bases; soluble ionic hydroxides such as NaOH are considered strong bases because they dissociate nearly completely when dissolved in water.
View the simulation of strong and weak acids and bases at the molecular level.
For example, the chemical reactions and ionization constants of the three bases are:
Consider the ionization reactions for a conjugate acid-base pair, HA and A−:
Adding these two chemical equations yields the equation for the autoionization of water:
The K expression for a chemical equation derived from adding two or more other equations is the mathematical product of the other equations’ K expressions. Multiplying the mass-action expressions together and cancelling common terms, we see that:
For example, the acid ionization constant of acetic acid (CH3COOH) is 1.8 × 10−5, and the base ionization constant of its conjugate base, acetate ion (CH3COO–), is 5.6 × 10−10. The product of these two constants is indeed equal to Kw:
The extent to which an acid, HA, donates protons to water molecules depends on the strength of its conjugate base, A−. If A− is a strong base, any protons that are donated to water molecules are recaptured by A−. Thus there is relatively little A− and H3O+ in solution, and the acid, HA, is weak. If A− is a weak base, water binds the protons more strongly, and the solution contains primarily A− and H3O+—the acid is strong. Strong acids form weak conjugate bases, and weak acids form strong conjugate bases (Figure 6).
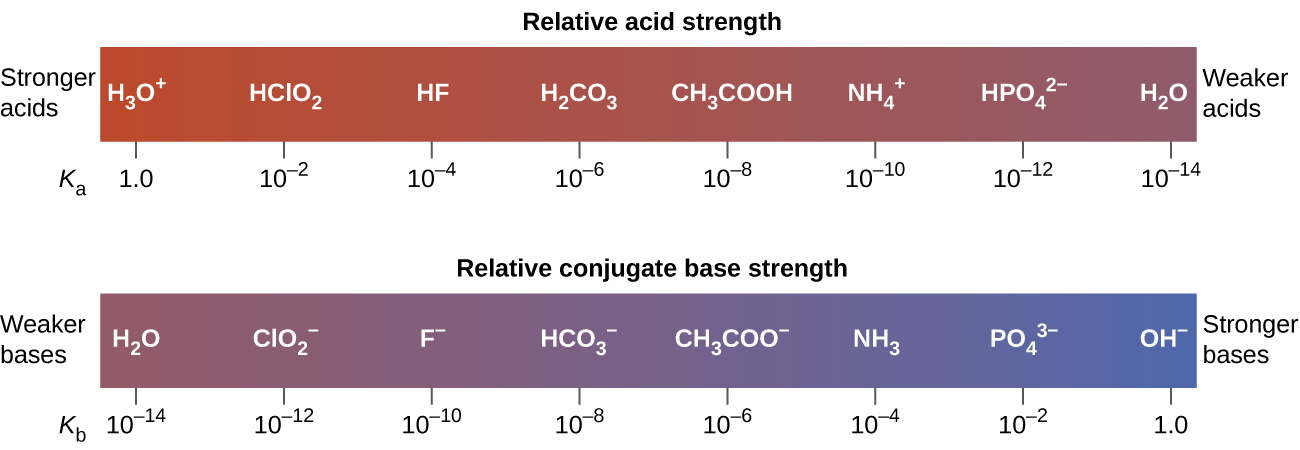
Figure 7 lists a series of acids and bases in order of the decreasing strengths of the acids and the corresponding increasing strengths of the bases. The acid and base in a given row are conjugate to each other.
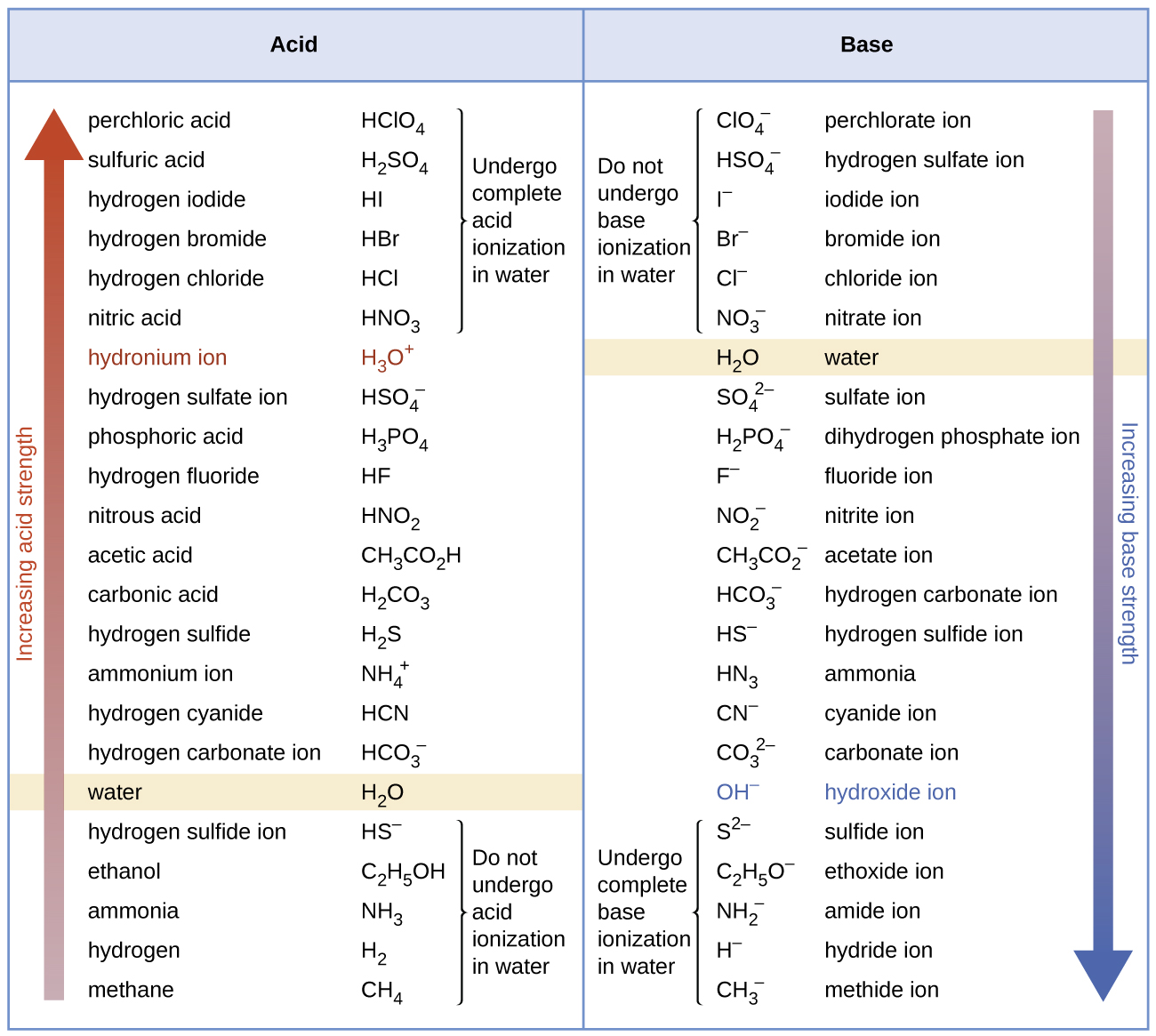
The first six acids in Figure 7 are the most common strong acids. These acids are neary completely dissociated in aqueous solution. The conjugate bases of these acids are weaker bases than water. When these acids dissolves in water, their protons are transferred to water, the stronger base.
The acids that lie between the hydronium ion and water in Figure 7 form conjugate bases that can compete with water for possession of a proton. Both hydronium ions and nonionized acid molecules are present in equilibrium in a solution of one of these acids.
Compounds that are weaker acids than water (those found below water in the column of acids) in Figure 7 exhibit almost no observable acidic behavior when dissolved in water. Their conjugate bases are stronger than the hydroxide ion, and if any conjugate base were formed, it would react with water to re-form the acid.
Similarly, the extent to which a base forms hydroxide ion in aqueous solution depends on the strength of the base relative to that of the hydroxide ion, as shown in the last column in Figure 7. A strong base, such as one lying below hydroxide ion, accepts protons from water to yield the conjugate acid and hydroxide ion. Those bases lying between water and hydroxide ion accept protons from water, but a mixture of the hydroxide ion and the base results. Bases that are weaker than water (those that lie above water in the column of bases) show no observable basic behavior in aqueous solution.
Example 7
The Product Ka × Kb = Kw
Use the Kb for the nitrite ion, NO2–, to calculate the Ka for its conjugate acid.
Solution
Kb for NO2– is given in this section as 2.17 × 10−11. The conjugate acid of NO2– is HNO2; Ka for HNO2 can be calculated using the relationship:
Solving for Ka, we get:
Check Your Learning
We can determine the relative acid strengths of NH4+ and HCN by comparing their ionization constants. The ionization constant of HCN is 4.9 × 10−10. The ionization constant of the conjugate base of NH4+, NH3, is 1.8 × 10−5. Determine the ionization constant of NH4+, and decide which is the stronger acid, HCN or NH4+.
Answer:
NH4+ is the slightly stronger acid (Ka for NH4+ = 5.6 × 10−10).
Ch15.6 Ionization of Weak Acids and Weak Bases
Many acids and bases are weak; that is, they do not ionize fully in aqueous solution. A solution of a weak acid in water is a mixture of the nonionized acid, hydronium ion, and the conjugate base of the acid, with the nonionized acid present in the greatest concentration. Thus, a weak acid increases the hydronium ion concentration in an aqueous solution (but not as much as the same amount of a strong acid).
Acetic acid, CH3CO2H, is a weak acid. When we add acetic acid to water, it ionizes to a small extent according to the equation:
and at equilibrium:
This equilibrium, like any other equilibria, is dynamic—acetic acid molecules donate protons to water molecules and form hydronium ions and acetate ions at the same rate that hydronium ions donate protons to acetate ions to reform acetic acid molecules and water molecules. We can tell by measuring the pH of an aqueous solution of known concentration that only a fraction of the weak acid is ionized at any moment (Figure 8).

Table 2 gives the ionization constants for several weak acids.
| Ionization Reaction | Ka at 25 °C |
|---|---|
| [latex]\text{HSO}_4^{\;\;-}\;+\;\text{H}_2\text{O}\;{\rightleftharpoons}\;\text{H}_3\text{O}^{+}\;+\;\text{SO}_4^{\;\;2-}[/latex] | 1.2 × 10−2 |
| [latex]\text{HF}\;+\;\text{H}_2\text{O}\;{\rightleftharpoons}\;\text{H}_3\text{O}^{+}\;+\;\text{F}^{-}[/latex] | 3.5 × 10−4 |
| [latex]\text{HNO}_2\;+\;\text{H}_2\text{O}\;{\rightleftharpoons}\;\text{H}_3\text{O}^{+}\;+\;\text{NO}_2^{\;\;-}[/latex] | 4.6 × 10−4 |
| [latex]\text{HCNO}\;+\;\text{H}_2\text{O}\;{\rightleftharpoons}\;\text{H}_3\text{O}^{+}\;+\;\text{NCO}^{-}[/latex] | 2 × 10−4 |
| [latex]\text{HCO}_2\text{H}\;+\;\text{H}_2\text{O}\;{\rightleftharpoons}\;\text{H}_3\text{O}^{+}\;+\;\text{HCO}_2^{\;\;-}[/latex] | 1.8 × 10−4 |
| [latex]\text{CH}_3\text{CO}_2\text{H}\;+\;\text{H}_2\text{O}\;{\rightleftharpoons}\;\text{H}_3\text{O}^{+}\;+\;\text{CH}_3\text{CO}_2^{\;\;-}[/latex] | 1.8 × 10−5 |
| [latex]\text{HCIO}\;+\;\text{H}_2\text{O}\;{\rightleftharpoons}\;\text{H}_3\text{O}^{+}\;+\;\text{CIO}^{-}[/latex] | 2.9 × 10−8 |
| [latex]\text{HBrO}\;+\;\text{H}_2\text{O}\;{\rightleftharpoons}\;\text{H}_3\text{O}^{+}\;+\;\text{BrO}^{-}[/latex] | 2.8 × 10−9 |
| [latex]\text{HCN}\;+\;\text{H}_2\text{O}\;{\rightleftharpoons}\;\text{H}_3\text{O}^{+}\;+\;\text{CN}^{-}[/latex] | 4.9 × 10−10 |
| Table 2. Ionization Constants of Some Weak Acids | |
At equilibrium, a solution of a weak base in water is a mixture of the nonionized base, the conjugate acid of the weak base, and hydroxide ion, with the nonionized base present in the greatest concentration. For example, a solution of the weak base trimethylamine, (CH3)3N, in water reacts according to the equation:
We can confirm by measuring the pH of an aqueous solution of a weak base of known concentration that only a fraction of the base reacts with water (Figure 9). The remaining weak base is present as the unreacted form.
The ionization constants of several weak bases are given in Table 3.
| Ionization Reaction | Kb at 25 °C |
|---|---|
| [latex](\text{CH}_3)_2\text{NH}\;+\;\text{H}_2\text{O}\;{\rightleftharpoons}\;(\text{CH}_3)_2\text{NH}_2^{\;\;+}\;+\;\text{OH}^{-}[/latex] | 5.9 × 10−4 |
| [latex]\text{CH}_3\text{NH}_2\;+\;\text{H}_2\text{O}\;{\rightleftharpoons}\;\text{CH}_3\text{NH}_3^{\;\;+}\;+\;\text{OH}^{-}[/latex] | 4.4 × 10−4 |
| [latex](\text{CH}_3)_3\text{N}\;+\;\text{H}_2\text{O}\;{\rightleftharpoons}\;(\text{CH}_3)_3\text{NH}^{+}\;+\;\text{OH}^{-}[/latex] | 6.3 × 10−5 |
| [latex]\text{NH}_3\;+\;\text{H}_2\text{O}\;{\rightleftharpoons}\;\text{NH}_4^{\;\;+}\;+\;\text{OH}^{-}[/latex] | 1.8 × 10−5 |
| [latex]\text{C}_6\text{H}_5\text{NH}_2\;+\;\text{H}_2\text{O}\;{\rightleftharpoons}\;\text{C}_6\text{N}_5\text{NH}_3^{\;\;+}\;+\;\text{OH}^{-}[/latex] | 4.3 × 10−10 |
| Table 3. Ionization Constants of Some Weak Bases | |
Example 8
Determination of Ka from Equilibrium Concentrations
Acetic acid is the principal ingredient in vinegar (Figure 10); that’s why it tastes sour. At equilibrium, a solution contains [CH3CO2H] = 0.0787 M and [H3O+] = [CH3CO2–] = 0.00118 M. What is the value of Ka for acetic acid?

Solution
We are asked to calculate an equilibrium constant from equilibrium concentrations for the reaction:
Check Your Learning
What is the equilibrium constant for the ionization of the HSO4– ion, the weak acid used in some household cleansers:
In one mixture of NaHSO4 and Na2SO4 at equilibrium, [H3O+] = 0.027 M; [HSO4–] = 0.29 M; and [SO42–] = 0.13 M.
Answer:
Ka for HSO4– = 1.2 x 10-2
Example 9
Determination of Kb from Equilibrium Concentrations
Caffeine, C8H10N4O2 is a weak base. What is the value of Kb for caffeine if a solution at equilibrium has [C8H10N4O2] = 0.050 M, [C8H10N4O2H+] = 5.0 × 10−3M, and [OH−] = 2.5 × 10−3M?
Solution
At equilibrium, for the reaction:
Check Your Learning
What is the equilibrium constant for the ionization of the HPO42- ion, a weak base:
In a solution containing a mixture of NaH2PO4 and Na2HPO4 at equilibrium, [OH−] = 1.3 × 10−6M; [H2PO4–] = 0.042 M; and [HPO42-] = 0.341 M.
Answer:
Kb for HPO42- = 1.6 x 10-7
Example 10
Determination of Ka or Kb from pH
The pH of a 0.0516-M solution of nitrous acid, HNO2, is 2.34. What is its Ka?
Solution
We determine an equilibrium constant starting with the initial concentrations of HNO2, H3O+, and NO2– as well as one of the final concentrations, the concentration of hydronium ion at equilibrium. (Remember that pH is simply another way to express the concentration of hydronium ion.)
We can solve this problem with the following steps in which x is a change in concentration of a species in the reaction:
![A diagram is shown that includes six rust-red rectangles. The first rectangle is labeled, “p H,” and there is an arrow that points to the right to the second rectangle. The second rectangle is labeled, “[ H subscript 3 O superscript plus ].” There is an arrow that points right to the third rectangle. The third rectangle is labeled, “Calculate x subscript [ H subscript 3 O superscript plus ].” There is an arrow that points right to the fourth rectangle. The fourth rectangle is labeled, “Calculate x subscript [ H N O subscript 2 ] and x subscript [ N O subscript 2 superscript negative sign ].” There is an arrow that points down to the fifth rectangle. The fifth rectangle is labeled, “Calculate equilibrium concentrations.” There is an arrow that points down to the sixth rectangle. The sixth rectangle is labeled, “Calculate K subscript a.”](https://wisc.pb.unizin.org/app/uploads/sites/126/2017/08/CNX_Chem_14_03_steps_img.jpg)
To get the various values in the ICE table, we first calculate [H3O+] at equilibrium from the pH:
The change in [H3O+], [latex]x_{[\text{H}_3\text{O}^{+}]}[/latex], is the difference between the equilibrium concentration of H3O+, which we determined from the pH, and the initial concentration. The initial concentration of H3O+ is its concentration in pure water, which is so much less than the final concentration that we approximate it as zero (~0).
The change in concentration of NO2– is equal to the change in concentration of H3O+. The equilibrium concentration of HNO2 is equal to its initial concentration plus the change in its concentration.
Now we can fill in the ICE table with the concentrations at equilibrium:
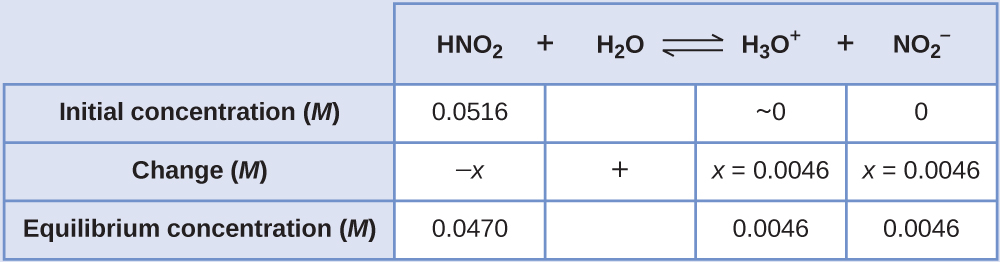
Finally, we calculate the value of the equilibrium constant using the data in the table:
Check Your Learning.
The pH of a solution of household ammonia, a 0.950-M solution of NH3, is 11.612. What is Kb for NH3.
Answer:
Kb = 1.8 × 10−5
Example 11
Equilibrium Concentrations in a Solution of a Weak Acid
Formic acid, HCO2H, is the irritant that causes the body’s reaction to ant bites (Figure 11).

What is the concentration of hydronium ion and the pH in a 0.534-M solution of formic acid?
Solution
- Determine x and equilibrium concentrations.The table shows initial concentrations (concentrations before the acid ionizes), changes in concentration, and equilibrium concentrations (the data given in the problem appear in color):
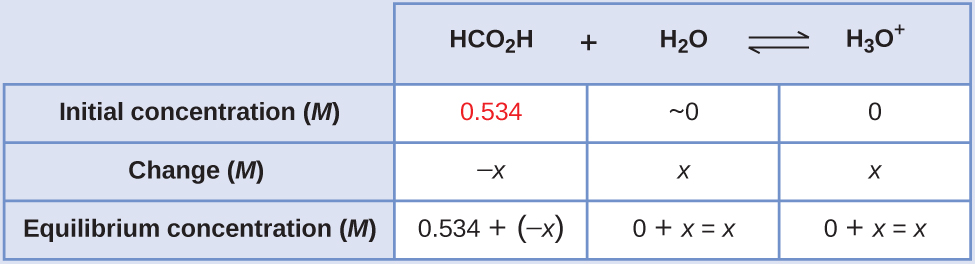
- Solve for x and the equilibrium concentrations.
At equilibrium:[latex]K_{\text{a}} = 1.8\;\times\;10^{-4} = \frac{[\text{H}_3\text{O}^{+}][\text{HCO}_2^{\;\;-}]}{[\text{HCO}_2\text{H}]}[/latex][latex]= \frac{(x)(x)}{0.534\;-\;x} = 1.8\;\times\;10^{-4}[/latex]solving this quadratic equation gives:
[latex]x = 9.7\;\times\;10^{-3}[/latex]We find the equilibrium concentration of hydronium ion in this formic acid solution from its initial concentration and the change in that concentration:
[latex][\text{H}_3\text{O}^{+}] = {\sim}0\;+\;x = 0\;+\;9.7\;\times\;10^{-3}\;M[/latex].[latex]= 9.7\;\times\;10^{-3}\;M[/latex]The pH of the solution can be found by taking the negative log of the [H3O+]:
[latex]-\text{log}(9.7\;\times\;10^{-3}) = 2.01[/latex]
The following example shows that the concentration of products produced by the ionization of a weak base can be determined by the same series of steps used with a weak acid.
Example 12
Equilibrium Concentrations in a Solution of a Weak Base
Find the concentration of hydroxide ion in a 0.25-M solution of trimethylamine, a weak base:
Solution
This problem requires that we calculate an equilibrium concentration by determining concentration changes as the ionization of a base goes to equilibrium. The solution is approached in the same way as that for the ionization of formic acid. The reactants and products will be different and the numbers will be different, but the logic will be the same:

- Determine x and equilibrium concentrations. The table shows the changes and concentrations
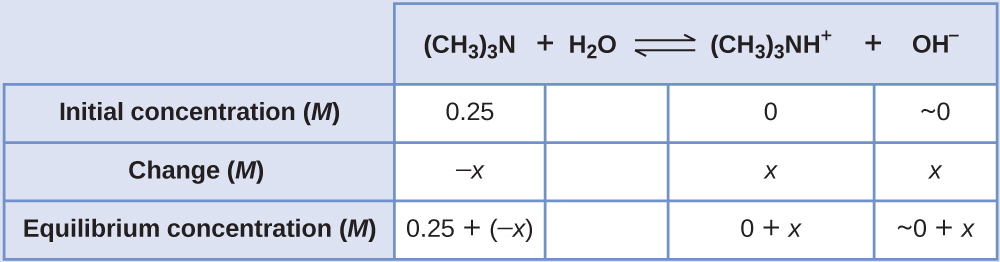
- Solve for x and the equilibrium concentrations. At equilibrium:
[latex]K_{\text{b}} = \frac{[(\text{CH}_3)_3\text{NH}^{+}][\text{OH}^{-}]}{[(\text{CH}_3)_3\text{N}]} = \frac{(x)(x)}{0.25\;-\;x} = 6.3\;\times\;10^{-5}[/latex]
If we assume that x is small relative to 0.25, then we can approximate 0.25 − x ≈ 0.25. Solving the simplified equation gives:
[latex]x = 4.0\;\times\;10^{-3}[/latex]To check the validity of the approximation: 0.25 – 0.0040 = 0.25, so the assumption is justified.
To obtain [OH–] and pOH:
[latex][\text{OH}^{-}] = {\sim}0\;+\;x = x = 4.0\;\times\;10^{-3}\;M[/latex][latex]\text{pOH} = -\text{log}(4.0\;\times\;10^{-3}) = 2.40[/latex]Using:
[latex]\text{pH}\;+\;\text{pOH} = \text{p}K_{\text{w}} = 14.00[/latex]we can also compute pH:
[latex]\text{pH} = 14.00\;-\;\text{pOH} = 14.00\;-\;2.40 = 11.60[/latex] - Check the work. A check of our arithmetic shows that Kb = 6.3 × 10−5.
Check Your Learning
Find the concentration of hydroxide ion in a 0.0325-M solution of ammonia, a weak base with a Kb of 1.76 × 10−5.
Answer:
7.56 × 10−4M
Example 13
Equilibrium Concentrations in a Solution of a Weak Acid
Sodium bisulfate, NaHSO4, is used in some household cleansers because it contains the HSO4–, a weak acid. What is the pH of a 0.50-M solution of HSO4−?
Solution
We need to determine the equilibrium concentration of the hydronium ion that results from the ionization of HSO4– so that we can use [H3O+] to determine the pH. As in the previous examples, we can approach the solution by the following steps:

- Determine x and equilibrium concentrations. This table shows the changes and concentrations:
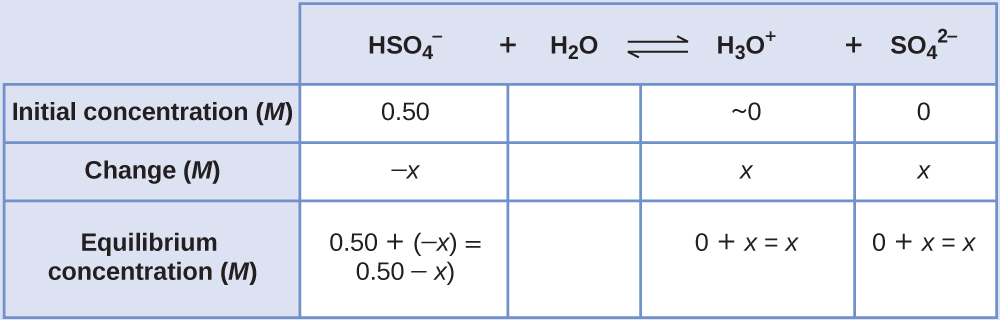
- Solve for x and the concentrations. At equilibrium:
[latex]K_{\text{a}} = 1.2\;\times\;10^{-2} = \frac{[\text{H}_3\text{O}^{+}][\text{SO}_4^{\;\;2-}]}{[\text{HSO}_4^{\;\;-}]} = \frac{(x)(x)}{0.50\;-\;x}[/latex]
which gives:
[latex]6.0\;\times\;10^{-3}\;-\;1.2\;\times\;10^{-2}x = x^{2}[/latex]or
[latex]x^{2}\;+\;1.2\;\times\;10^{-2}x\;-\;6.0\;\times\;10^{-3} = 0[/latex]This equation can be solved using the quadratic formula. For an equation of the form
[latex]ax^{2}\;+\;bx\;+\;c = 0[/latex],x is given by the equation:
[latex]x = \frac{-b\;{\pm}\;\sqrt{b^{2}\;-\;4\text{ac}}}{2a}[/latex]In this problem, a = 1, b = 1.2 × 10−3, and c = −6.0 × 10−3.
Solving for x gives a negative root (which cannot be correct since concentration cannot be negative) and a positive root:
[latex]x = 7.2\;\times\;10^{-2}[/latex]Now determine the hydronium ion concentration and the pH:
[latex][\text{H}_3\text{O}^{+}] = {\sim}0\;+\;x = 0\;+\;7.2\;\times\;10^{-2}\;M[/latex][latex]= 7.2\;\times\;10^{-2}\;M[/latex]The pH of this solution is:
[latex]\text{pH} = -\text{log}[\text{H}_3\text{O}^{+}] = -\text{log}\;(7.2\;\times\;10^{-2}) = 1.14[/latex]
Check Your Learning
(b) Calculate the pH in a 0.010-M solution of caffeine, a weak base:
(Hint: It will be necessary to convert [OH−] to [H3O+] or pOH to pH toward the end of the calculation.)
Answer:
pH 11.16
Ch15.7 Relative Strengths of Strong Acids and Bases
Strong acids, such as HCl, HBr, and HI, all exhibit the same strength in water. The water molecule is such a strong base compared to the conjugate bases Cl−, Br−, and I− that ionization of these strong acids is essentially complete in aqueous solutions. In solvents less basic than water, we find HCl, HBr, and HI differ markedly in their tendency to give up a proton to the solvent. For example, when dissolved in ethanol (a weaker base than water), the extent of ionization increases in the order HCl < HBr < HI, and so HI is demonstrated to be the strongest of these acids. The inability to discern differences in strength among strong acids dissolved in water is known as the leveling effect of water.
Water also exerts a leveling effect on the strengths of strong bases. For example, the oxide ion, O2−, and the amide ion, NH2–, are such strong bases that they react completely with water:
Thus, O2− and [latex]\text{NH}_2^{\;\;-}[/latex] appear to have the same base strength in water; they both give a 100% yield of hydroxide ion.
Ch15.8 Acid Strength and Molecular Structure
If we consider a generic acid:
In general, the stronger the A–H bond, the less likely the bond is to break to form H+ ions and thus the less acidic the substance. This effect can be illustrated using the hydrogen halides:
| Relative Acid Strength | HF | HCl | HBr | HI |
|---|---|---|---|---|
| H–X Bond Energy (kJ/mol) | 570 | 432 | 366 | 298 |
| pKa | 3.20 | −6.1 | −8.9 | −9.3 |
The trend in bond energies is due to a steady decrease in overlap between the 1s orbital of hydrogen and the valence orbital of the halogen atom as the size of the halogen increases. The larger the atom to which H is bonded, the weaker the bond. Thus the bond between H and a large atom in a given family, such as I or Te, is weaker than the bond between H and a smaller atom in the same family, such as F or O. As a result, acid strengths of binary hydrides increase as we go down a column of the periodic table. For example, the order of acidity for the binary hydrides of Group 16 elements is as follows, with pKa values in parentheses:
The stability of the conjugate base also has an effect on the acidity. For the acid HA, the conjugate base (A−) contains one more lone pair of electrons than the parent acid. Any factor that stabilizes the lone pair (i.e. the excess negative charge) on the conjugate base favors dissociation of H+ and makes the parent acid a stronger acid. Let’s see how this explains the relative acidity of the binary hydrides of the elements in the second row of the periodic table. The observed order of increasing acidity is the following, with pKa values in parentheses:
Consider, for example, the compounds at both ends of this series: methane and hydrogen fluoride. The conjugate base of CH4 is CH3–, and the conjugate base of HF is F−. Because fluorine is much more electronegative than carbon, fluorine can better stabilize the negative charge in the F− ion than carbon can stabilize the negative charge in the CH3− ion. Consequently, HF has a greater tendency to dissociate to form H+ and F− than does methane to form H+ and CH3–, making HF a much stronger acid than CH4.
The same trend is predicted by analyzing the properties of the conjugate acids. For a series of compounds of the general formula HA, as the electronegativity of “A” increases, the A–H bond becomes more polar, favoring dissociation to form A− and H+. Due to both the increasing stability of the conjugate base and the increasing polarization of the A–H bond in the conjugate acid, acid strengths of binary hydrides increase as we go from left to right across a row of the periodic table.
The effect of stability of conjugate base is also at play when we consider the acidity of carboxylic acids. The pKa ‘s of some typical carboxylic acids are listed in the following table. When we compare these values with those of comparable alcohols, such as ethanol (pKa = 16) and 2-methyl-2-propanol (pKa = 19), it is clear that carboxylic acids are stronger acids by over ten powers of ten.
| Compound | pKa | Compound | pKa | |
|---|---|---|---|---|
| HCO2H | 3.75 | CH3CH2CH2CO2H | 4.82 | |
| CH3CO2H | 4.74 | ClCH2CH2CH2CO2H | 4.53 | |
| FCH2CO2H | 2.65 | CH3CHClCH2CO2H | 4.05 | |
| ClCH2CO2H | 2.85 | CH3CH2CHClCO2H | 2.89 | |
| BrCH2CO2H | 2.90 | C6H5CO2H | 4.20 | |
| ICH2CO2H | 3.10 | p-O2NC6H4CO2H | 3.45 | |
| Cl3CCO2H | 0.77 | p-CH3OC6H4CO2H | 4.45 |
Why should the presence of a carbonyl group adjacent to a hydroxyl group have such a profound effect on the acidity of the hydroxyl proton? To answer this question we must return to the nature of acid-base equilibria and the definition of pKa , illustrated by the general equations given below.
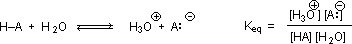

We know that an equilibrium favors the thermodynamically more stable side, and that the magnitude of the equilibrium constant reflects the energy difference between the components of each side. In an acid base equilibrium the equilibrium always favors the weaker acid and base (these are the more stable components). Consequently, anything that stabilizes the conjugate base (A–) of an acid will necessarily make that acid (H–A) stronger and shift the equilibrium to the right. Both the carboxyl group and the carboxylate anion are stabilized by resonance, but the stabilization of the anion is much greater than that of the neutral function, as shown in the following diagram. In the carboxylate anion the two contributing structures have equal weight in the hybrid, and the C–O bonds are of equal length (between a double and a single bond). This stabilization leads to a markedly increased acidity.

Atoms (or groups of atoms) in a molecule that are not directly bonded to the acidic H can also influence the molecule’s acidity, by inducing a change in the distribution of electrons within the molecule. This is called an inductive effect. This can be seen in the table above where electronegative substituents near the carboxyl group act to increase the acidity. The magnitude of the inductive effect depends on both the nature and the number of halogen substituents, as shown by the pKa values for several acetic acid derivatives:
As you might expect, fluorine, which is more electronegative than chlorine, causes a larger effect than chlorine, and the effect of three halogens is greater than the effect of two or one. Notice from these data that inductive effects can be quite large. For instance, replacing the –CH3 group of acetic acid by a –CF3 group results in about a 10,000-fold increase in acidity!
In another example, the hypohalous acids (general formula HOX, with X representing a halogen) all have a hydrogen atom bonded to an oxygen atom. In aqueous solution, they all produce the following equilibrium:
The acidities of these acids vary by about three orders of magnitude due to the difference in electronegativity of the halogen atoms:
| HOX | Electronegativity of X | pKa |
|---|---|---|
| HOCl | 3.0 | 7.40 |
| HOBr | 2.8 | 8.55 |
| HOI | 2.5 | 10.5 |
As the electronegativity of X increases, the distribution of electron density within the molecule changes: the electrons are drawn more strongly toward the halogen atom and, in turn, away from the H in the O–H bond, thus weakening the O–H bond and allowing dissociation of hydrogen as H+.
The acidity of oxoacids, with the general formula HOXOn (with n = 0−3), depends strongly on the number of terminal oxygen atoms attached to the central atom X. As shown in Figure 12, the Ka values of the oxoacids of chlorine increase by a factor of about 104 to 106 with each oxygen as successive oxygen atoms are added. The increase in acid strength with increasing number of terminal oxygen atoms is due to both an inductive effect and increased stabilization of the conjugate base.
Any inductive effect that withdraws electron density from an O–H bond increases the acidity of the compound. Because oxygen is the second most electronegative element, adding terminal oxygen atoms causes electrons to be drawn away from the O–H bond, making it weaker and thereby increasing the strength of the acid. The colors in Figure 12 show how the electrostatic potential, a measure of the strength of the interaction of a point charge at any place on the surface of the molecule, changes as the number of terminal oxygen atoms increases. In Figure 12 and Figure 13, blue corresponds to low electron densities, while red corresponds to high electron densities. The oxygen atom in the O–H unit becomes steadily less red from HClO to HClO4, while the H atom becomes steadily bluer, indicating that the electron density on the O–H unit decreases as the number of terminal oxygen atoms increases. The decrease in electron density in the O–H bond weakens it, making it easier to lose hydrogen as H+ ions, thereby increasing the strength of the acid.

At least as important is also the effect of delocalization of the negative charge in the conjugate base. As shown in Figure 13, the number of important resonance structures that can be written for the oxoanions of chlorine increases as the number of terminal oxygen atoms increases, indicating that the single negative charge is delocalized over successively more oxygen atoms.
Electron delocalization in the conjugate base increases acid strength. The electrostatic potential plots in Figure 13 demonstrate that the electron density on the terminal oxygen atoms decreases steadily as their number increases. The oxygen atom in ClO− is red, indicating that it is electron rich, and the color of oxygen progressively changes to green in ClO4–, indicating that the oxygen atoms are becoming steadily less electron rich through the series. For example, in the perchlorate ion (ClO4–), the single negative charge is delocalized over all four oxygen atoms, whereas in the hypochlorite ion (ClO−), the negative charge is largely localized on a single oxygen atom. As a result, the perchlorate ion has no localized negative charge to which a proton can bind. Consequently, the perchlorate anion has a much lower affinity for a proton than does the hypochlorite ion, and perchloric acid is one of the strongest acids known.

Inductive effects are also responsible for the trend in the acidities of oxoacids that have the same number of oxygen atoms as we go across a row of the periodic table from left to right. For example, H3PO4 is a weak acid, H2SO4 is a strong acid, and HClO4 is one of the strongest acids known. The number of terminal oxygen atoms increases steadily across the row, consistent with the observed increase in acidity. In addition, the electronegativity of the central atom increases steadily from P to S to Cl, which causes electrons to be drawn from oxygen to the central atom, weakening the O–H bond and increasing the strength of the oxoacid.
Ch15.9 Percent Ionization
Another measure of the strength of an acid is its percent ionization. The percent ionization of a weak acid is the ratio of the concentration of the ionized acid to the initial acid concentration, times 100:
Because the ratio includes the initial concentration, the percent ionization for a solution of a given weak acid varies depending on the original concentration of the acid, and actually decreases with increasing acid concentration.
Example 14
Calculation of Percent Ionization from pH
Calculate the percent ionization of a 0.125-M solution of nitrous acid (a weak acid), with a pH of 2.09.
Solution
The percent ionization for an acid is:
The chemical equation for the dissociation of the nitrous acid is:
Since
we find that 10−2.09 = 8.1 × 10−3M, so that percent ionization is:
(the logarithm 2.09 indicates a hydronium ion concentration with only two significant figures.)
Check Your Learning
Calculate the percent ionization of a 0.10-M solution of acetic acid with a pH of 2.89.
Answer:
1.3% ionized
Ch15.10 Polyprotic Acids
We can classify acids by the number of protons per molecule that they can give up in an acid-base reaction. Acids such as HCl, HNO3, and HCN that contain one ionizable hydrogen atom in each molecule are called monoprotic acids. Their reactions with water are:
Even though it contains four hydrogen atoms, acetic acid, CH3CO2H, is also monoprotic because only the hydrogen atom from the carboxyl group (-COOH) reacts with bases:

Similarly, monoprotic bases are bases that will accept a single proton.
Diprotic acids contain two ionizable hydrogen atoms per molecule; ionization of such acids occurs in two steps. The first ionization always takes place to a greater extent than the second ionization. For example, sulfuric acid, a strong acid, ionizes as follows:
This stepwise ionization process occurs for all polyprotic acids. When we make a solution of a weak diprotic acid, we get a solution that contains a mixture of acids. Carbonic acid, H2CO3, is an example of a weak diprotic acid. The first ionization of carbonic acid yields hydronium ions and bicarbonate ions in small amounts.
The bicarbonate ion can also act as an acid. It ionizes and forms hydronium ions and carbonate ions in even smaller quantities.
[latex]K_{\text{H}_2\text{CO}_3}[/latex] is larger than [latex]K_{\text{HCO}_3^{\;-}}[/latex] by a factor of 104, so H2CO3 is the dominant producer of hydronium ion in the solution. This means that little of the HCO3– formed by the ionization of H2CO3 ionizes to give hydronium ions (and carbonate ions), and the concentrations of H3O+ and HCO3– are practically equal in a pure aqueous solution of H2CO3.
If the first ionization constant of a weak diprotic acid is larger than the second by a factor of at least 20, it is appropriate to treat the first ionization separately and calculate concentrations resulting from it before calculating concentrations of species resulting from subsequent ionization. This can simplify our work considerably because we can determine the concentration of H3O+ and the conjugate base from the first ionization, then determine the concentration of the conjugate base of the second ionization in a solution with concentrations determined by the first ionization.
Example 15
Ionization of a Diprotic Acid
When we buy soda water (carbonated water), we are buying a solution of carbon dioxide in water. The solution is acidic because CO2 reacts with water to form carbonic acid, H2CO3. What are [H3O+], [HCO3–], and [CO32-] in a saturated solution of CO2 with an initial [H2CO3] = 0.033 M?
Solution
As indicated by the ionization constants, H2CO3 is a much stronger acid than HCO3–, so H2CO3 is the dominant producer of hydronium ion in solution. Thus there are two parts in the solution of this problem: (1) Using the customary four steps, we determine the concentration of H3O+ and HCO3– produced by ionization of H2CO3. (2) Then we determine the concentration of CO32- in a solution with the concentration of H3O+ and HCO3– determined in (1). To summarize:
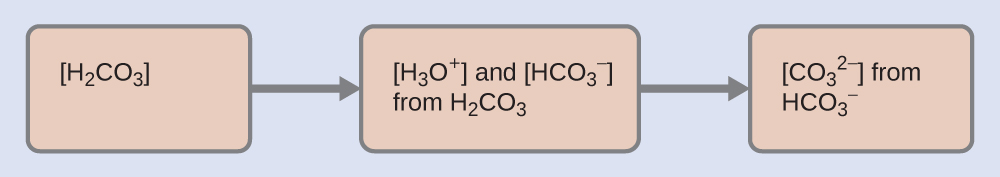
- Determine the concentrations of H3O+ and HCO3–.
[latex]\text{H}_2\text{CO}_3(aq)\;+\;\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;\text{H}_3\text{O}^{+}(aq)\;+\;\text{HCO}_3^{\;\;-}(aq)\;\;\;\;\;\;\;K_{\text{a}1} = 4.3\;\times\;10^{-7}[/latex]
For the ionization of weak acid:

An ICE table shows:
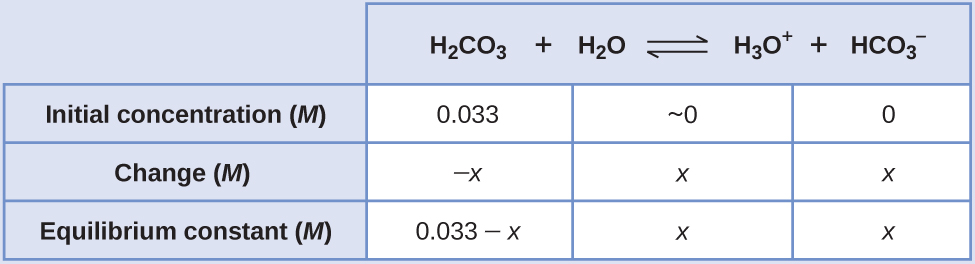
Substituting in the equilibrium concentrations gives us:
[latex]K_{\text{H}_2\text{CO}_3} = \frac{[\text{H}_3\text{O}^{+}][\text{HCO}_3^{\;\;-}]}{[\text{H}_2\text{CO}_3]} = \frac{(x)(x)}{0.033\;-\;x} = 4.3\;\times\;10^{-7}[/latex]Solving for x gives:
[latex]x = 1.2\;\times\;10^{-4}[/latex]Thus:
[latex][\text{H}_2\text{CO}_3] = 0.033\;M[/latex][latex][\text{H}_3\text{O}^{+}] = [\text{HCO}_3^{\;\;-}] = 1.2\;\times\;10^{-4}\;M[/latex] - Determine the concentration of CO32- in a solution at equilibrium with [H3O+] and [HCO3–], both equal to 1.2 ×10−4 M.
[latex]\text{HCO}_3^{\;\;-}(aq)\;+\;\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;\text{H}_3\text{O}^{+}(aq)\;+\;\text{CO}_3^{\;\;2-}(aq)\;\;K_{\text{a}2} = 5.6\;\times\;10^{-11}[/latex][latex]K_{\text{HCO}_3^{\;\;-}} = \frac{[\text{H}_3\text{O}^{+}][\text{CO}_3^{\;\;2-}]}{[\text{HCO}_3^{\;\;-}]} = \frac{(1.2\;\times\;10^{-4})[\text{CO}_3^{\;\;2-}]}{1.2\;\times\;10^{-4}}[/latex][latex][\text{CO}_3^{\;\;2-}] = \frac{(5.6\;\times\;10^{-11})(1.2\;\times\;10^{-4})}{1.2\;\times\;10^{-4}} = 5.6\;\times\;10^{-11}\;M[/latex]
To summarize: In part 1 of this example, we found that the H2CO3 in a 0.033-M solution ionizes slightly and at equilibrium [H2CO3] = 0.033 M; [latex][\text{H}_3\text{O}^{+}] = 1.2\;\times\;10^{-4}\;M[/latex]; and [latex][\text{HCO}_3^{\;\;-}] = 1.2\;\times\;10^{-4}\;M[/latex]. In part 2, we determined that [latex][\text{CO}_3^{\;\;2-}] = 5.6\;\times\;10^{-11}\;M[/latex].
Check Your Learning
The concentration of H2S in a saturated aqueous solution at room temperature is approximately 0.1 M. Calculate [H3O+], [HS−], and [S2−] in the solution:
Answer:
[H2S] = 0.1 M; [H3O+] = [HS−] = 0.000094 M; [S2−] = 1 × 10−19M
We note that the concentration of the sulfide ion is the same as Ka2. This is due to the fact that each subsequent dissociation occurs to a lesser degree (as acid gets weaker).
A triprotic acid is an acid that has three dissociable protons that undergo stepwise ionization: Phosphoric acid is a typical example:
As with the diprotic acids, the differences in the ionization constants of these reactions tell us that in each successive step the degree of ionization is significantly weaker. This is a general characteristic of polyprotic acids.
This set of three dissociation reactions may appear to make calculations of equilibrium concentrations in a solution of H3PO4 complicated. However, because the successive ionization constants differ by a factor of 105 to 106, the calculations can be broken down into a series of parts similar to those for diprotic acids.
Polyprotic bases can accept more than one hydrogen ion in solution. The carbonate ion is an example of a diprotic base, since it can accept up to two protons. Solutions of alkali metal carbonates are quite alkaline, due to the reactions:
Ch15.11 Strong Acid Reacting with Strong Base
When we mix solutions of an acid and a base, an acid-base neutralization reaction occurs.
A strong acid and a strong base, such as HCl(aq) and NaOH(aq), will react to form a neutral solution if we mix stoichiometrically equivalent quantities, since the conjugate partners produced are of negligible strength:
A solution is neutral when it contains equal concentrations of hydronium and hydroxide ions.
Stomach Antacids
Our stomachs contain a solution of roughly 0.03 M HCl, which helps us digest the food we eat. The burning sensation associated with heartburn is a result of the stomach acid leaking through the muscular valve at the top of the stomach into the lower reaches of the esophagus. The lining of the esophagus is not protected from the corrosive effects of stomach acid the way the lining of the stomach is, and the results can be very painful. When we have heartburn, it feels better if we reduce the excess acid in the esophagus by taking an antacid. As you may have guessed, antacids are bases. One of the most common antacids is calcium carbonate, CaCO3. The reaction
not only neutralizes stomach acid, it also produces CO2(g), which may result in a satisfying belch.
Milk of Magnesia is a suspension of the sparingly soluble base magnesium hydroxide, Mg(OH)2. It works according to the reaction:
The hydroxide ions generated in this equilibrium then go on to react with the hydronium ions from the stomach acid, so that :
This reaction does not produce carbon dioxide, but magnesium-containing antacids can have a laxative effect.
Several antacids have aluminum hydroxide, Al(OH)3, as an active ingredient. The aluminum hydroxide tends to cause constipation, and some antacids use aluminum hydroxide in concert with magnesium hydroxide to balance the side effects of the two substances.
Ch15.12 Strong Acid Reacting with Weak Base
When we mix a weak base with a strong acid, the product is a salt containing the conjugate acid of the weak base. This conjugate acid is a weak acid. For example, ammonium chloride, NH4Cl, is a salt formed by the reaction of the weak base ammonia with the strong acid HCl:
A solution of this salt contains ammonium ions and chloride ions. The chloride ion has no effect on the acidity of the solution since HCl is a strong acid. Chloride is a very weak base and will not accept a proton to a measurable extent. However, the ammonium ion, the conjugate acid of ammonia, reacts with water and increases the hydronium ion concentration:
The equilibrium equation for this reaction is simply the ionization constant, Ka, for the acid NH4+:
Example 16
The pH of a Solution of a Weak Base and a Strong Acid
Aniline is an amine that is used to manufacture dyes. It is isolated as aniline hydrochloride, [C6H5NH3]Cl, a salt prepared by the reaction of the weak base aniline and hydrochloric acid. What is the pH of a 0.233 M solution of aniline hydrochloride? (Kb for aniline, C6H5NH2, is 4.3 × 10−10)
Solution
The new step in this example is to determine Ka for the C6H5NH3+ ion, the conjugate acid of a weak base. We can determine value of Ka for this acid from the value of Kb for aniline:
Now we have the ionization constant and the initial concentration of the weak acid, the information necessary to determine the equilibrium concentration of H3O+, and the pH:

With these steps we find [H3O+] = 2.3 × 10−3M and pH = 2.64
Check Your Learning
(a) Do the calculations and show that the hydronium ion concentration for a 0.233-M solution of C6H5NH3+ is 2.3 × 10−3 and the pH is 2.64.
(b) What is the hydronium ion concentration in a 0.100-M solution of ammonium nitrate, NH4NO3, a salt composed of the ions NH4+ and NO3–. The Kb for ammonia is 1.8 × 10−5. Which is the stronger acid C6H5NH3+ or NH4+?
Answer:
(a) Ka(forNH4+) = 5.6 × 10-10, [H3O+] = 7.5 × 10−6 M; (b) C6H5NH3+ is the stronger acid.
Ch15.13 Weak Acid Reacting with Strong Base
When we mix a weak acid with a strong base, we get a salt that contains the conjugate base of the weak acid. This conjugate base is usually a weak base. For example, sodium acetate, NaCH3CO2, is a salt formed by the reaction of the weak acid acetic acid with the strong base sodium hydroxide:
A solution of this salt contains sodium ions and acetate ions. The sodium ion, as the conjugate acid of a strong base, has no effect on the acidity of the solution. However, the acetate ion, the conjugate base of acetic acid, reacts with water and increases the concentration of hydroxide ion:
The equilibrium equation for this reaction is the ionization constant, Kb, for the base CH3CO2–.
Some reference tables do not report values of Kb. They only report ionization constants for acids. The value of Kb can be calculated from the value of the ionization constant of water, Kw, and Ka, the ionization constant of the conjugate acid of the base.
Example 17
Equilibrium in a Solution of a Weak Acid and a Strong Base
Determine the acetic acid concentration in a solution with [CH3CO2–] = 0.050 M and [OH−] = 2.5 × 10−6M at equilibrium. (Ka for acetic acid is 1.8 × 10-5) The reaction is:
Solution
We are given two of three equilibrium concentrations and asked to find the missing concentration. If we can find the equilibrium constant for the reaction, the process is straightforward.
The acetate ion behaves as a base in this reaction; hydroxide ions are a product. We determine Kb as follows:
Now find the missing concentration:
Solving this equation we get [CH3CO2H] = 1.1 × 10−5M.
Check Your Learning
What is the pH of a 0.083-M solution of CN−? Use 4.9 × 10−10 as Ka for HCN. Hint: We will probably need to convert pOH to pH or find [H3O+] using [OH−] in the final stages of this problem.
Answer:
11.11
Ch15.14 Weak Acid Reacting with Weak Base
In a solution of a salt formed by the reaction of a weak acid and a weak base, to predict the pH, we must know both the Ka of the weak acid and the Kb of the weak base. If Ka > Kb, the solution is acidic, and if Kb > Ka, the solution is basic.
Example 18
Determining the Acidic or Basic Nature of Salts
Determine whether aqueous solutions of the following salts are acidic, basic, or neutral:
(a) KBr
(b) NaHCO3
(c) NH4Cl
(d) Na2HPO4
(e) NH4F
Solution
Consider each of the ions separately in terms of its effect on the pH of the solution:
(a) The K+ cation and the Br− anion are both spectators, since they are the conjugate acid of a strong base (KOH) and the conjugate base of a strong acid (HBr), respectively. The solution is neutral.
(b) The Na+ cation is a spectator, and will not affect the pH of the solution. The HCO3– anion is amphiprotic, it could either behave as an acid or a base. The Ka of HCO3– is 4.7 × 10−11, the Kb of HCO3– (from Ka of H2CO3) is [latex]\frac{1.0\;\times\;10^{-14}}{4.3\;\times\;10^{-7}} = 2.3\;\times\;10^{-8}[/latex].
Since Kb > Ka, the solution is basic.
(c) The NH4+ ion is acidic and the Cl− ion is a spectator. The solution will be acidic.
(d) The Na+ ion is a spectator. while the HPO42- is amphiprotic, with a Ka of 4.2 × 10−13 and a Kb of 1.6 × 10^-7. Because Kb > Ka, the solution is basic.
(e) The NH4+ ion is acidic, and the F− ion is a base, so we must directly compare the Ka and the Kb of the two ions. Ka of NH4+ is 5.6 × 10−10, which seems very small, but the Kb of F− is 1.4 × 10−11, even smaller. So the solution is acidic, since Ka > Kb.
Check Your Learning
Determine whether aqueous solutions of the following salts are acidic, basic, or neutral:
(a) K2CO3
(b) CaCl2
(c) KH2PO4
(d) (NH4)2CO3
(e) AlBr3
Answer:
(a) basic; (b) neutral; (c) acidic; (d) basic; (e) acidic
Ch15.15 Reaction Between Amphiprotic Species
Acid-base reactions can also occur between two amphiprotic species. For example, when you mix hydrogen sulfite (HSO3–) and bicarbonate (HCO3–) solutions, acid-base reaction will occur. But if both species can act as either an acid or a base, how do you tell which species will act as which? In the example mixture, we can envision two scenarios:
scenario II: HSO3–(aq) + HCO3–(aq) ⇌ H2SO3(aq) + CO32-(aq)
Quantitatively, we can make use of the ionization constants to determine which set of products is more favored and hence which scenario is the dominant one. In scenario I, we have:
HCO3–(aq) + H3O+(aq) ⇌ H2CO3(aq) + H2O(l) [latex]K_2 = \dfrac{1}{K_{\text{a, H}_2\text{CO}_3}} = \dfrac{1}{4.3\;\times\;10^{-7}}[/latex]
Hence, the reaction HSO3–(aq) + HCO3–(aq) ⇌ SO32-(aq) + H2CO3(aq) has a total equilibrium constant of:
In scenario II, we have:
HCO3–(aq) + H2O(l) ⇌ CO32-(aq) + H3O+(aq) [latex]K_2 = K_{\text{a, HCO}_3^-} = 4.7\;\times\;10^{-11}[/latex]
Hence, the reaction HSO3–(aq) + HCO3–(aq) ⇌ H2SO3(aq) + CO32-(aq) has a total equilibrium constant of:
Scenario I is significantly more product-favored than scenario II, Ktotal, I >> Ktotal, II. Therefore, we would expect HSO3– to act as the acid and to HCO3– act as the base.
Qualitatively, H2CO3 (with Ka = 4.3 × 10-7) is less acidic than H2SO3 (with Ka = 1.7 × 10-2); SO32- (with Kb = 1.6 × 10-7) is less basic than CO32- (with Kb = 2.1 × 10-4). Hence, the reaction leading to the formation of H2CO3 and SO32- (scenario I) is thermodynamically more favorable than the reaction leading to the formation of H2SO3 and CO32- (scenario II).
Ch15.16 Amino Acids
Another important group of amphiprotic species is the amino acids. Each amino acid molecule contains an carboxyl group and an amino group. We have seen that carboxylic acids are moderately acidic. Most of them have pKa in the range of 3 to 5. We have also seen that organic amines are somewhat basic, and are easily protonated if protons are available.
Because the carboxylic acid is a pretty good source of protons and because protons bind to amines pretty well, it seems reasonable that a proton transfer may occur from one site to the other.
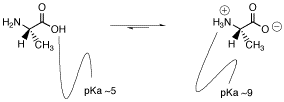
Does one of these forms dominate the equilibrium? Compare the pKa values. The pKa of the acid is near 5, and the pKa of the ammonium is near 9. The ammonium holds the proton more tightly than does the acid. The proton stays on the nitrogen.
This is analogous to the acid-base reaction between methylamine (Kb = 4.4 × 10-4) and acetic acid (Ka = 1.8 × 10-5):
where the equilibrium would favor the product-side because:
In fact, amino acids usually exist in zwitterion (German for “double ion”) form, where the proton has transferred from the carboxyl to the amino group. A zwitterion is a compound with no overall electrical charge, but which contains separate parts which are positively and negatively charged.
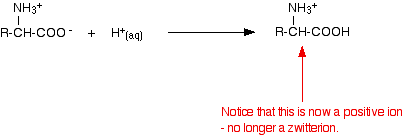
If you increase the pH of a solution of an amino acid by adding hydroxide ions, the hydrogen ion is removed from the -NH3+ group.

If you decrease the pH by adding an acid to a solution of an amino acid, the -COO– part of the zwitterion picks up a hydrogen ion.