Additional Reading Materials
Chapter 11: Thermochemistry and Enthalphy
Ch11.1 Thermal Energy, Temperature, and Heat
Thermal energy is kinetic energy associated with the random motion of atoms and molecules. Temperature is a quantitative measure of “hot” or “cold.” When the atoms and molecules in an object are moving or vibrating quickly, they have a higher average kinetic energy (KE), and we say that the object is “hot.” When the atoms and molecules are moving slowly, they have lower KE, and we say that the object is “cold”. Assuming that no chemical reaction or phase change (such as melting or vaporizing) occurs, increasing the amount of thermal energy in a sample of matter will cause its temperature to increase. Similarly, decreasing thermal energy will cause temperature to decrease.
Click on this interactive simulation to view the effects of temperature on molecular motion.
Most substances expand as their temperature increases and contract as their temperature decreases. This property can be used to measure temperature changes, as shown in Figure 1. The operation of many thermometers depends on the expansion and contraction of substances in response to temperature changes.
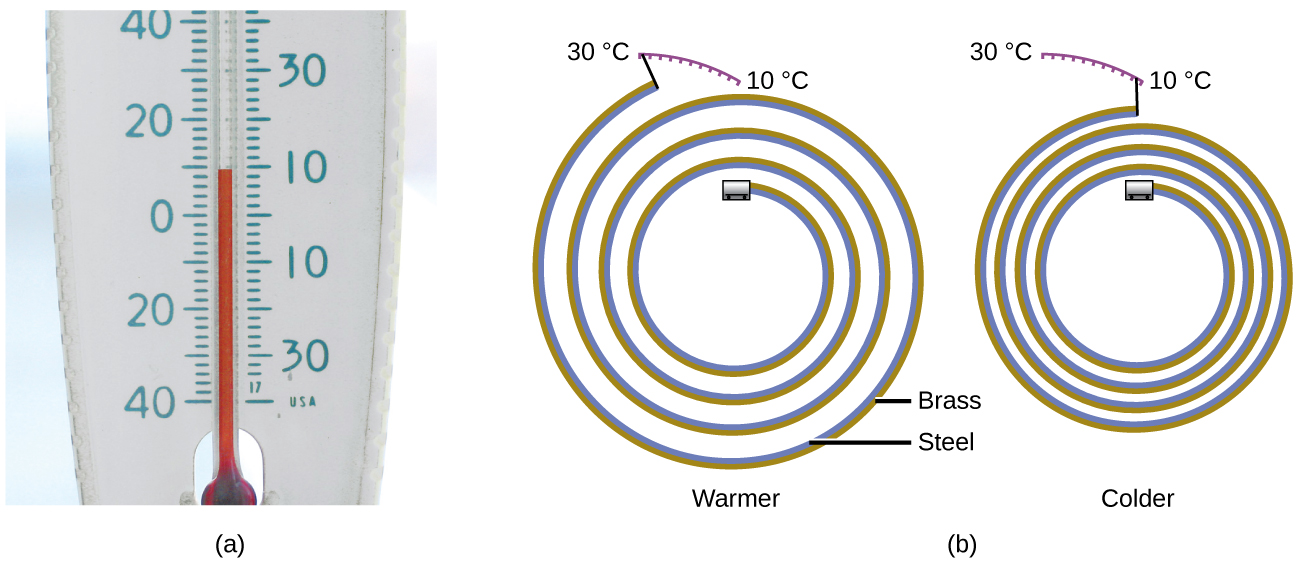
The following demonstration allows one to view the effects of heating and cooling a coiled bimetallic strip.
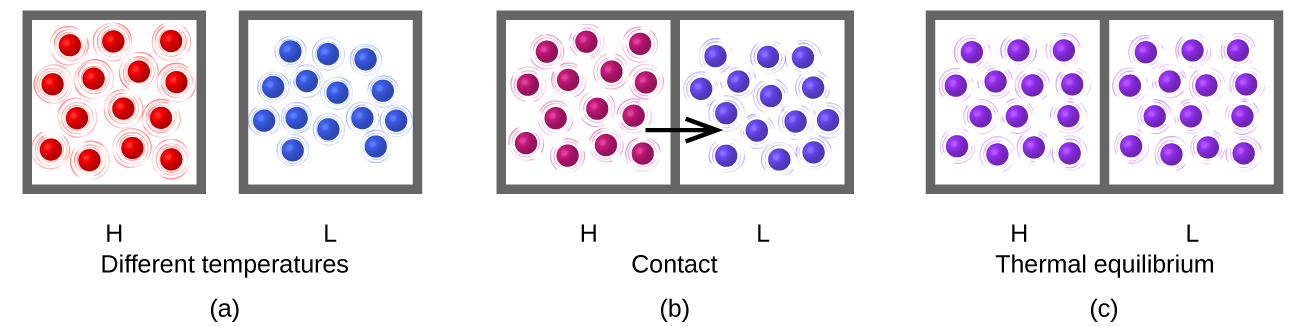
Heat (q) is the transfer of thermal energy between two bodies at different temperatures. Suppose we initially have a high temperature (and high thermal energy) substance (H) and a low temperature (and low thermal energy) substance (L). The molecules in H have a higher average KE than those in L. If we place substance H in contact with substance L, the thermal energy will flow from substance H to substance L. The temperature of substance H will decrease, as will the average KE of its molecules; the temperature of substance L will increase, along with the average KE of its molecules. Thermal energy transfer will continue until the two substances are at the same temperature (Figure 2).
Click on the PhET simulation to explore energy forms and changes. Visit the Energy Systems tab to create combinations of energy sources, transformation methods, and outputs. Click on Energy Symbols to visualize the transfer of energy.
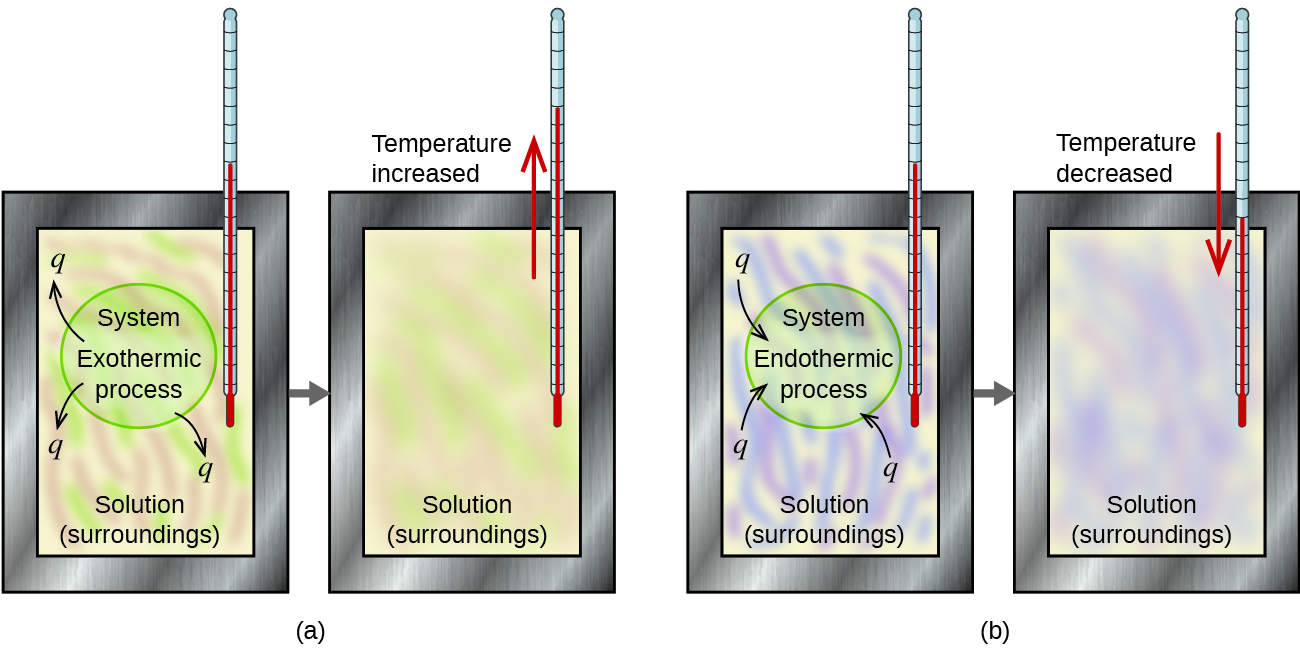
Matter undergoing chemical reactions and physical changes can release or absorb heat. A change that releases heat is called an exothermic process. For example, the combustion reaction that occurs when using an oxyacetylene torch is an exothermic process—this process also releases energy in the form of light as evidenced by the torch’s flame (Figure 3). A reaction or change that absorbs heat is an endothermic process. A cold pack used to treat muscle strains provides an example of an endothermic process. When the substances in the cold pack (water and a salt such as ammonium nitrate) are brought together, the resulting process absorbs heat, making the pack cold.

Historically, energy was measured in units of calories (cal). A calorie is the amount of energy required to raise one gram of water by 1 degree C (1 kelvin). However, this quantity depends on the atmospheric pressure and the starting temperature of the water. The ease of measurement of energy changes in calories has meant that the calorie is still frequently used. The Calorie (with a capital C), or large calorie, commonly used in quantifying food energy content, is a kilocalorie. The SI unit of heat, work, and energy is the joule. A joule (J) is defined as the amount of energy used when a force of 1 newton moves an object 1 meter. It is named in honor of the English physicist James Prescott Joule. One joule is equivalent to 1 kg m2/s2, which is also called 1 newton–meter. To standardize its definition, 1 calorie has been set to equal 4.184 joules.
The heat capacity (C) of a body of matter is the quantity of heat (q) it absorbs or releases when it experiences a temperature change (ΔT) of 1 degree Celsius (or equivalently, 1 kelvin):
Heat capacity is determined by both the type and the amount of substance that absorbs or releases heat. It is therefore an extensive property—its value is proportional to the amount of the substance.
For example, consider the heat capacities of two cast iron frying pans.(Figure 4) Although both are made of the same material, the mass of the large pan is five times greater, and more mass means more atoms are present in the larger pan, so it takes more energy to make all of those atoms vibrate faster.
The heat capacity of the small cast iron frying pan is found by observing that it takes 18,150 J of energy to raise the temperature of the pan by 50.0 °C:
The larger cast iron frying pan requires 90,700 J of energy to raise its temperature by 50.0 °C. The larger pan has a five times larger heat capacity because the larger amount of material requires a (proportionally) larger amount of energy to yield the same temperature change:
The specific heat capacity (c) of a substance, commonly called its “specific heat,” is the quantity of heat required to raise the temperature of 1 gram of a substance by 1 degree Celsius (or 1 kelvin):
Specific heat capacity depends only on the kind of substance absorbing or releasing heat. It is an intensive property—the type, but not the amount, of the substance is all that matters. For example, the small cast iron frying pan has a mass of 808 g. The specific heat of iron (the material used to make the pan) is therefore:
The large frying pan has a mass of 4040 g. Using the data for this pan, we can also calculate the specific heat of iron:
Since both are made of the same material, they both yield the same value for specific heat. (Figure 4) Note that specific heat is measured in units of energy per temperature per mass and is an intensive property, being derived from a ratio of two extensive properties (heat and mass). The molar heat capacity, also an intensive property, is the heat capacity per mole of a particular substance and has units of J/mol °C.

Liquid water has a relatively high specific heat (about 4.2 J/g °C); most metals have much lower specific heats (usually less than 1 J/g °C). The specific heat of a substance varies somewhat with temperature. However, this variation is usually small enough that we will treat specific heat as constant over the range of temperatures that will be considered in this course. Specific heats of some common substances are listed in Table 1.
| Substance | Symbol (state) | Specific Heat (J/g °C) |
|---|---|---|
| helium | He(g) | 5.193 |
| water | H2O(l) | 4.184 |
| ethanol | C2H6O(l) | 2.376 |
| ice | H2O(s) | 2.093 (at −10 °C) |
| water vapor | H2O(g) | 1.864 |
| nitrogen | N2(g) | 1.040 |
| oxygen | O2(g) | 0.918 |
| aluminum | Al(s) | 0.897 |
| carbon dioxide | CO2(g) | 0.853 |
| argon | Ar(g) | 0.522 |
| iron | Fe(s) | 0.449 |
| copper | Cu(s) | 0.385 |
| lead | Pb(s) | 0.130 |
| gold | Au(s) | 0.129 |
| silicon | Si(s) | 0.712 |
| Table 1. Specific Heats of Common Substances at 25 °C and 1 bar | ||
If we know the mass of a substance and its specific heat, we can determine the amount of heat, q, entering or leaving the substance by measuring the temperature change before and after the heat is gained or lost:
If a substance gains thermal energy, its temperature increases, its ΔT is positive, and the value of q is positive. If a substance loses thermal energy, its temperature decreases, its ΔT is negative, and the value of q is negative.
Example 1
Measuring Heat
A flask containing 8.0 × 102 g of water is heated, and the temperature of the water increases from 21 °C to 85 °C. How much heat did the water absorb?
Solution
To answer this question, consider these factors:
- the specific heat of the substance being heated (in this case, water)
- the amount of substance being heated (in this case, 800 g)
- the magnitude of the temperature change (in this case, from 21 °C to 85 °C).
The specific heat of water is 4.184 J/g °C. Since 4.184 J is required to heat 1 g of water by 1 °C, we will need 800 times as much to heat 800 g of water by 1 °C. And, we will need 64 times as much to heat it by 64 °C (that is, from 21 °C to 85 °C).
This can be summarized using the equation:
Because the temperature increased, the water absorbed heat and q is positive.
Check Your Learning
How much heat, in joules, must be added to a 5.00 × 102-g iron skillet to increase its temperature from 25 °C to 250 °C? The specific heat of iron is 0.451 J/g °C.
Answer:
5.07 × 104 J
Note that the relationship between heat, specific heat, mass, and temperature change can be used to determine any of these quantities (not just heat) if the other three are known or can be deduced.
Example 2
Determining Other Quantities
A piece of unknown metal weighs 348 g. When the metal piece absorbs 6.64 kJ of heat, its temperature increases from 22.4 °C to 43.6 °C. Determine the specific heat of this metal (which might provide a clue to its identity).
Solution
Since mass, heat, and temperature change are known for this metal, we can determine its specific heat using the relationship:
Substituting the known values:
Solving:
Comparing this value with the values in Table 1, this value matches the specific heat of aluminum, which suggests that the unknown metal may be aluminum.
Check Your Learning
A piece of unknown metal weighs 217 g. When the metal piece absorbs 1.43 kJ of heat, its temperature increases from 24.5 °C to 39.1 °C. Determine the specific heat of this metal, and predict its identity.
Answer:
c = 0.45 J/g °C; the metal is likely to be iron
Note: Solar Thermal Energy Power Plants
The sunlight that reaches the earth contains thousands of times more energy than we presently capture. Solar thermal systems provide one possible solution to the problem of converting energy from the sun into energy we can use. Large-scale solar thermal plants have different design specifics, but all concentrate sunlight to heat some substance; the heat “stored” in that substance is then converted into electricity.
The Solana Generating Station in Arizona’s Sonora Desert produces 280 megawatts of electrical power. It uses parabolic mirrors that focus sunlight on pipes filled with a heat transfer fluid (HTF) (Figure 5). The HTF then does two things: It turns water into steam, which spins turbines, which in turn produces electricity, and it melts and heats a mixture of salts, which functions as a thermal energy storage system. After the sun goes down, the molten salt mixture can then release enough of its stored heat to produce steam to run the turbines for 6 hours. Molten salts are used because they possess a number of beneficial properties, including high heat capacities and thermal conductivities.
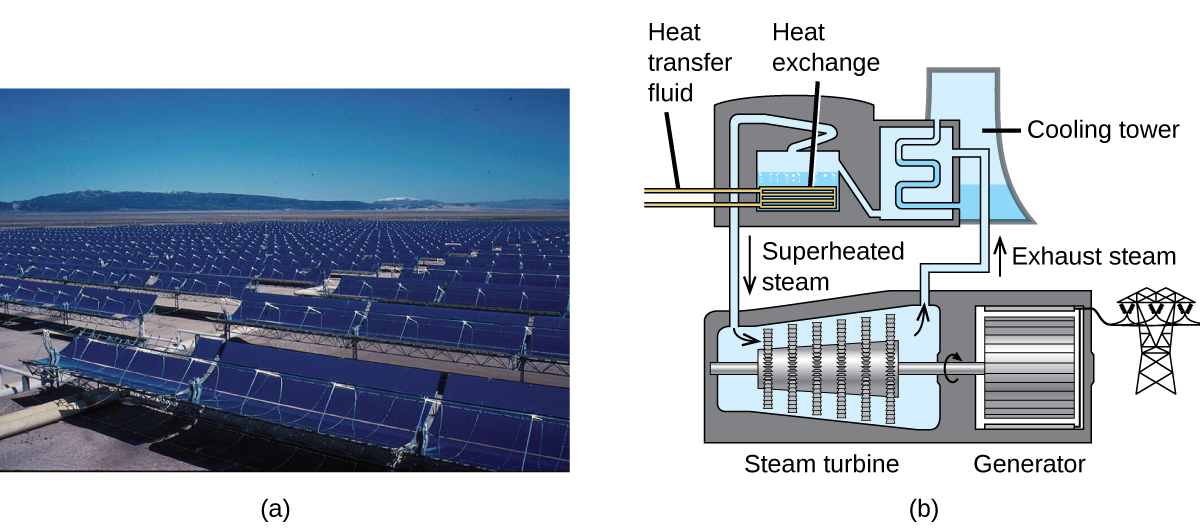
The 377-megawatt Ivanpah Solar Generating System, located in the Mojave Desert in California, is the largest solar thermal power plant in the world (Figure 6). Its 170,000 mirrors focus huge amounts of sunlight on three water-filled towers, producing steam at over 538 °C that drives electricity-producing turbines. It produces enough energy to power 140,000 homes. Water is used as the working fluid because of its large heat capacity and heat of vaporization.

Ch11.2 Calorimetry
Calorimetry is used to measure amounts of heat transferred to or from a substance. To do so, the heat is exchanged with a calibrated object (calorimeter). The change in temperature of the measuring part of the calorimeter is converted into the amount of heat. The measurement of heat transfer using this approach requires the definition of a system (the substance or substances undergoing the chemical or physical change) and its surroundings (the other components of the measurement apparatus that serve to either provide heat to the system or absorb heat from the system). Knowledge of the heat capacity of the surroundings, and careful measurements of the masses of the system and surroundings and their temperatures before and after the process allows one to calculate the heat transferred.
For example, when an exothermic reaction occurs in solution in a calorimeter, the heat produced by the reaction is absorbed by the solution, which increases its temperature. When an endothermic reaction occurs, the heat required is absorbed from the thermal energy of the solution, which decreases its temperature (Figure 7). The temperature change, along with the specific heat and mass of the solution, can then be used to calculate the amount of heat involved in either case.
Scientists use well-insulated calorimeters that all but prevent the transfer of heat between the calorimeter and its environment. This enables the accurate determination of the heat involved in chemical processes, the energy content of foods, and so on. General chemistry students often use simple calorimeters constructed from polystyrene cups (Figure 8). These easy-to-use “coffee cup” calorimeters allow more heat exchange with their surroundings, and therefore produce less accurate energy values.
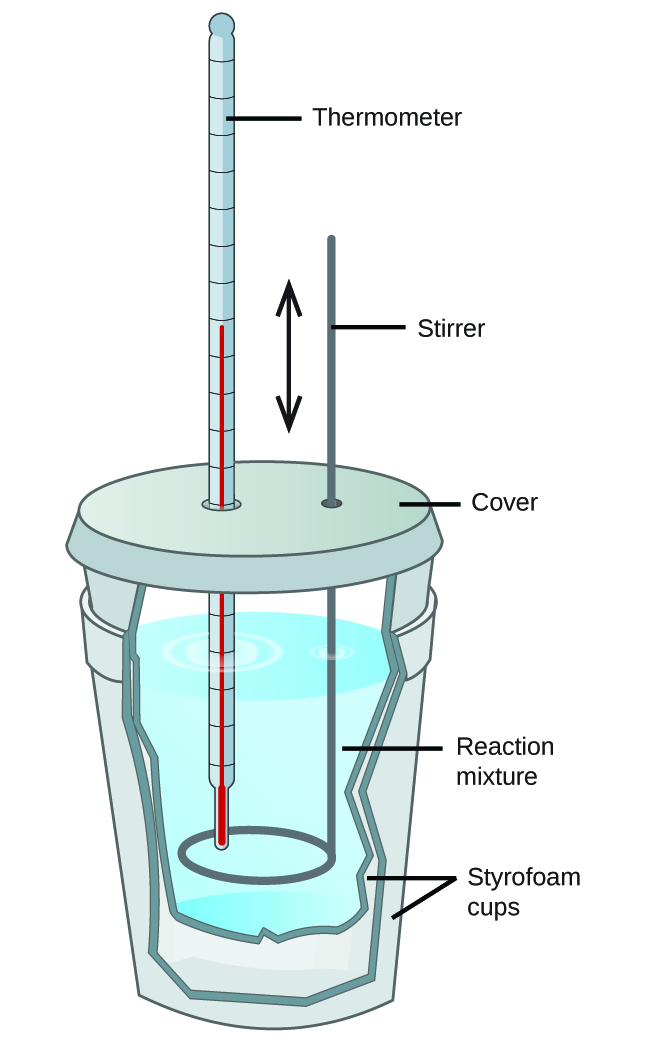
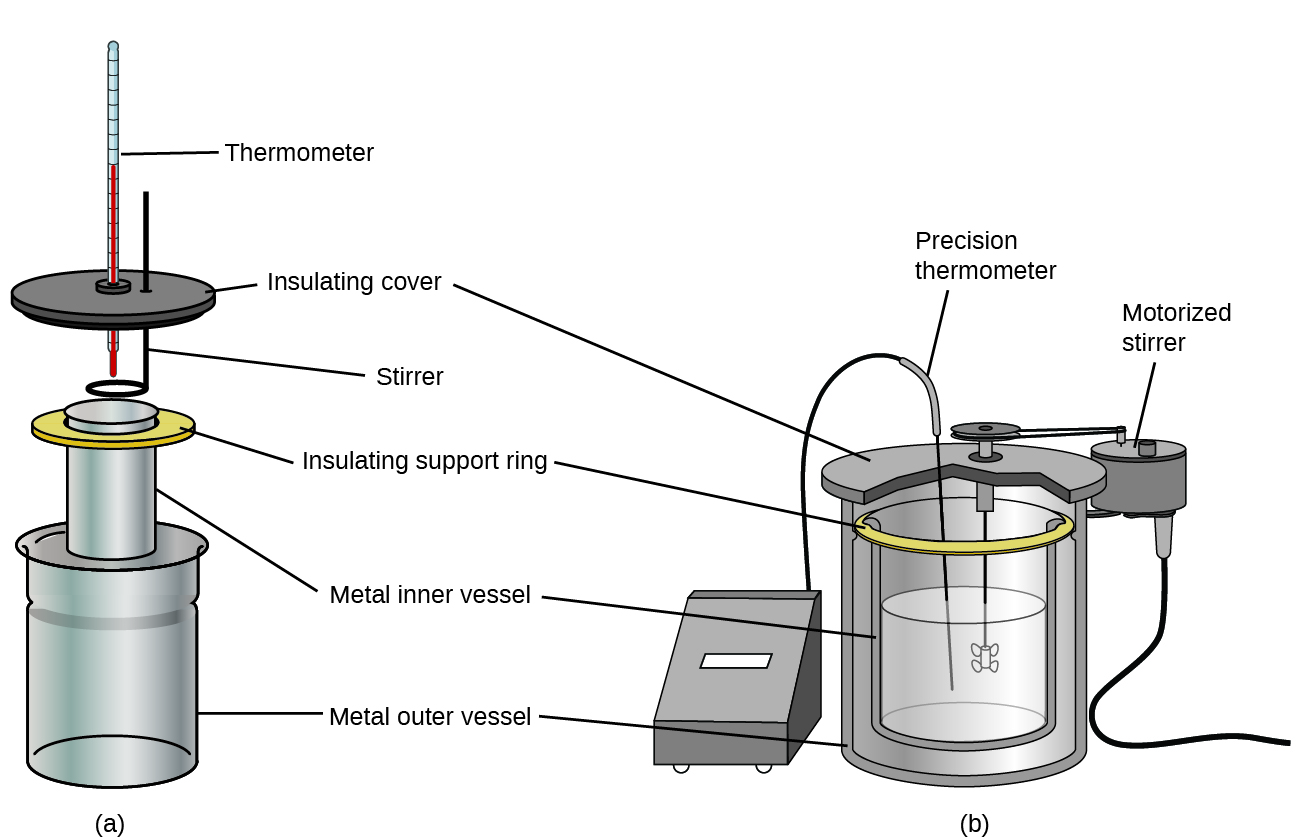
Commercial solution calorimeters are also available. Relatively inexpensive calorimeters often consist of two thin-walled cups that are nested in a way that minimizes thermal contact during use, along with an insulated cover, handheld stirrer, and simple thermometer. More expensive calorimeters used for industry and research typically have a well-insulated, fully enclosed reaction vessel, motorized stirring mechanism, and a more accurate temperature sensor (Figure 9).
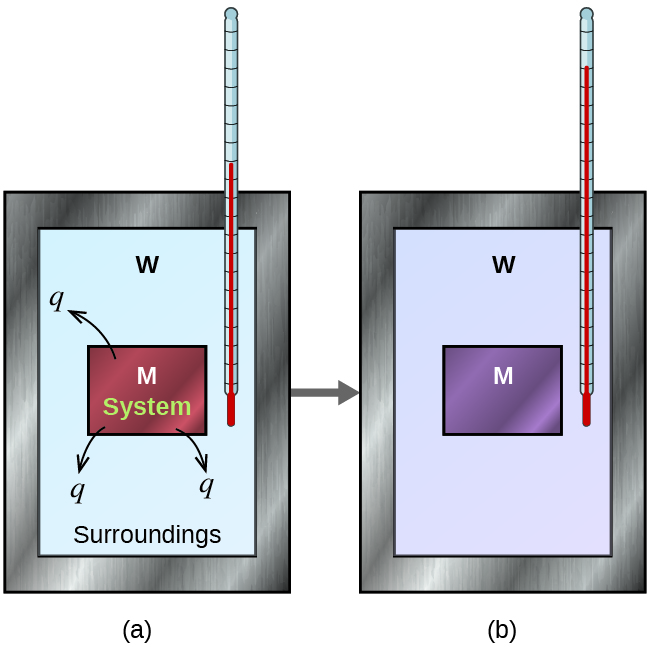
Before we practice calorimetry problems involving chemical reactions, consider a simpler example that illustrates the core idea behind calorimetry. Suppose we initially have a hot piece of metal (M) and cool water (W). If we place the metal in the water, heat will flow from M to W. The temperature of M will decrease, and the temperature of W will increase, until the two substances have the same temperature—that is, when they reach thermal equilibrium (Figure 10). If this occurs in a calorimeter, ideally all of this heat transfer occurs between the two substances, with no heat gained or lost by either the calorimeter or the calorimeter’s surroundings. Under these ideal circumstances, the net heat change is zero:
qM + qW = 0
This relationship can be rearranged to show that the heat gained by W is equal to the heat lost by M:
qW = -qM
The magnitude of the heat (change) is therefore the same for both substances, and the negative sign merely shows that qM and qW are opposite in direction of heat flow (gain or loss) but does not indicate the arithmetic sign of either q value (that is determined by whether the matter in question gains or loses heat). In the situation described, qM is negative and qW is positive.
Example 3
Heat Transfer between Substances at Different Temperatures
A 360-g piece of rebar (a steel rod used for reinforcing concrete) is dropped into 425 g of water at 24.0 °C. The final temperature of the water was measured as 42.7 °C. Calculate the initial temperature of the piece of rebar. Assume the specific heat of steel is approximately 0.449 J/g ºC, and that all heat transfer occurs between the rebar and the water.
Solution
The temperature of the water increases from 24.0 °C to 42.7 °C, so the water absorbs heat. That heat came from the piece of rebar, which initially was at a higher temperature. Assuming that all heat transfer was between the rebar and the water, then heat given off by rebar = −heat taken in by water, or:
Letting f = final and i = initial, in expanded form, this becomes:
Noting that the final temperature of both the rebar and water is 42.7 °C, substituting known values yields:
[latex]T_{\text{i, rebar}} = \frac{(4.184 \;\text{J/g} \;^\circ\text{C})(425 \;\text{g})(42.7 \;^\circ\text{C} - 24.0 \;^\circ\text{C})}{(0.449 \;\text{J/g} \;^\circ\text{C})(360 \;\text{g})} + 42.7 \;^\circ\text{C}[/latex]
Solving this gives Ti,rebar= 248 °C.
Check Your Learning
A 248-g piece of copper is dropped into 390 g of water at 22.6 °C. The final temperature of the water was measured as 39.9 °C. Calculate the initial temperature of the piece of copper. Assume that all heat transfer occurs between the copper and the water.
Answer:
The initial temperature of the copper was 335.6 °C.
Check Your Learning
A 248-g piece of copper initially at 314 °C is dropped into 390 g of water initially at 22.6 °C. Assuming that all heat transfer occurs between the copper and the water, calculate the final temperature.
Answer:
The final temperature (reached by both copper and water) is 38.7 °C.
Example 4
Identifying a Metal by Measuring Specific Heat
A 59.7 g piece of metal that had been submerged in boiling water was quickly transferred into 60.0 g of water initially at 22.0 °C. The final temperature is 28.5 °C. Use these data to determine the specific heat of the metal. Use this result to identify the metal.
Solution
Assuming perfect heat transfer:
Noting that since the metal was submerged in boiling water, its initial temperature was 100.0 °C, we have:
Solving this:
Comparing this with values in Table 1, our experimental specific heat is closest to the value for copper (0.385 J/g °C), so we identify the metal as copper.
Check Your Learning
A 92.9-g piece of a silver/gray metal is heated to 178.0 °C, and then quickly transferred into 75.0 g of water initially at 24.0 °C. After 5 minutes, both the metal and the water have reached the same temperature: 29.7 °C. Determine the specific heat and the identity of the metal. (Note: You should find that the specific heat is close to that of two different metals. Explain how you can confidently determine the identity of the metal).
Answer:
cmetal= 0.13 J/g °C
This specific heat is close to that of either gold or lead. It would be difficult to determine which metal this was based solely on the numerical values. However, the observation that the metal is silver/gray in addition to the value for the specific heat indicates that the metal is lead.
The same principles apply when we use calorimetry to determine the heat involved in a chemical reaction: the heat produced or consumed in the reaction (the “system”), qreaction, plus the heat absorbed or lost by the solution (the “surroundings”), qsolution, add up to zero:
This means that the amount of heat produced or consumed in the reaction equals the amount of heat absorbed or lost by the solution:
This concept lies at the heart of all calorimetry problems and calculations.
Example 5
Heat Produced by an Exothermic Reaction
When 50.0 mL of 0.10 M HCl(aq) and 50.0 mL of 0.10 M NaOH(aq), both at 22.0 °C, are added to a coffee cup calorimeter, the temperature of the mixture reaches a maximum of 28.9 °C. What is the approximate amount of heat produced by this reaction?
Solution
To visualize what is going on, imagine that you could combine the two solutions so quickly that no reaction took place; then after mixing, the reaction took place. At the instant of mixing, you have 100.0 mL of a mixture of HCl and NaOH at 22.0 °C. The HCl and NaOH then react until the solution temperature reaches 28.9 °C.
The heat given off by the reaction is equal to that taken in by the solution. Therefore:
(It is important to remember that this relationship only holds if the calorimeter does not absorb any heat from the reaction, and there is no heat exchange between the calorimeter and its surroundings.)
Next, we know that the heat absorbed by the solution depends on its specific heat, mass, and temperature change:
To proceed with this calculation, we need to make a few more reasonable assumptions or approximations. Since the solution is aqueous, we can proceed as if it were water in terms of its specific heat and mass values. The density of water is approximately 1.0 g/mL, so 100.0 mL has a mass of about 1.0 × 102 g (two significant figures). The specific heat of water is approximately 4.18 J/g °C, so we use that for the specific heat of the solution. Substituting these values gives:
Finally, since we are trying to find the heat of the reaction, we have:
The negative sign indicates that the reaction is exothermic. It produces 2.89 kJ of heat.
Check Your Learning
When 100 mL of 0.200 M NaCl(aq) and 100 mL of 0.200 M AgNO3(aq), both at 21.9 °C, are mixed in a coffee cup calorimeter, the temperature increases to 23.5 °C as solid AgCl forms. How much heat is produced by this precipitation reaction? What assumptions did you make to determine your value?
Answer:
1.34 × 103 J; assume no heat is absorbed by the calorimeter, no heat is exchanged between the calorimeter and its surroundings, and that the specific heat and mass of the solution are the same as those for water
Thermochemistry of Hand Warmers
When working or playing outdoors on a cold day, you might use a hand warmer to warm your hands (Figure 11). A common reusable hand warmer contains a supersaturated solution of NaC2H3O2 (sodium acetate) and a metal disc. Bending the disk creates nucleation sites around which the metastable NaC2H3O2 quickly crystallizes.
The process [latex]\text{NaC}_2 \text{H}_3 \text{O}_2 (aq) \longrightarrow \text{NaC}_2 \text{H}_3 \text{O}_2 (s)[/latex] is exothermic, and the heat produced by this process is absorbed by your hands, thereby warming them (at least for a while). If the hand warmer is reheated, the NaC2H3O2 redissolves and can be reused.

Another common hand warmer produces heat when it is ripped open, exposing iron and water in the hand warmer to oxygen in the air. One simplified version of this exothermic reaction is [latex]2\text{Fe}(s) + \frac{3}{2}\text{O}_2(g) \longrightarrow \text{Fe}_2\text{O}_3(s)[/latex]. Salt in the hand warmer catalyzes the reaction, so it produces heat more rapidly; cellulose, vermiculite, and activated carbon help distribute the heat evenly. Other types of hand warmers use lighter fluid (a platinum catalyst helps lighter fluid oxidize exothermically), charcoal (charcoal oxidizes in a special case), or electrical units that produce heat by passing an electrical current from a battery through resistive wires.
This link shows the precipitation reaction that occurs when the disk in a chemical hand warmer is flexed.
Example 6
Heat Flow in an Instant Ice Pack
When solid ammonium nitrate dissolves in water, the solution becomes cold. This is the basis for an “instant ice pack” (Figure 12). When 3.21 g of solid NH4NO3 dissolves in 50.0 g of water at 24.9 °C in a calorimeter, the temperature decreases to 20.3 °C.
Calculate the value of q for this reaction and explain the meaning of its arithmetic sign. State any assumptions that you made.

Solution
We assume that the calorimeter prevents heat transfer between the solution and its external environment (including the calorimeter itself), in which case:
Assuming also that the specific heat of the solution is the same as that for water, we have:
The positive sign for q indicates that the dissolution is an endothermic process.
Check Your Learning
When a 3.00-g sample of KCl was added to 3.00 × 102 g of water in a coffee cup calorimeter, the temperature decreased by 1.05 °C. How much heat is involved in the dissolution of the KCl? What assumptions did you make?
Answer:
1.33 kJ; assume that the calorimeter prevents heat transfer between the solution and its external environment (including the calorimeter itself) and that the specific heat of the solution is the same as that for water
If the amount of heat absorbed by a calorimeter is too large to neglect or if we require more accurate results, then we must take into account the heat absorbed both by the solution and by the calorimeter.
The calorimeters described are designed to operate at constant (atmospheric) pressure and are convenient to measure heat flow accompanying processes that occur in solution. A different type of calorimeter that operates at constant volume, colloquially known as a bomb calorimeter, is used to measure the energy produced by reactions that yield large amounts of heat and gaseous products, such as combustion reactions. (The term “bomb” comes from the observation that these reactions can be vigorous enough to resemble explosions that would damage other calorimeters.) This type of calorimeter consists of a robust steel container (the “bomb”) that contains the reactants and is itself submerged in water (Figure 13). The sample is placed in the bomb, which is then filled with oxygen at high pressure. A small electrical spark is used to ignite the sample. The energy produced by the reaction is trapped in the steel bomb and the surrounding water. The temperature increase is measured and, along with the known heat capacity of the calorimeter, is used to calculate the energy produced by the reaction. Bomb calorimeters require calibration to determine the heat capacity of the calorimeter and ensure accurate results. The calibration is accomplished using a reaction with a known q, such as a measured quantity of benzoic acid ignited by a spark from a nickel fuse wire that is weighed before and after the reaction. The temperature change produced by the known reaction is used to determine the heat capacity of the calorimeter. The calibration is generally performed each time before the calorimeter is used to gather research data.
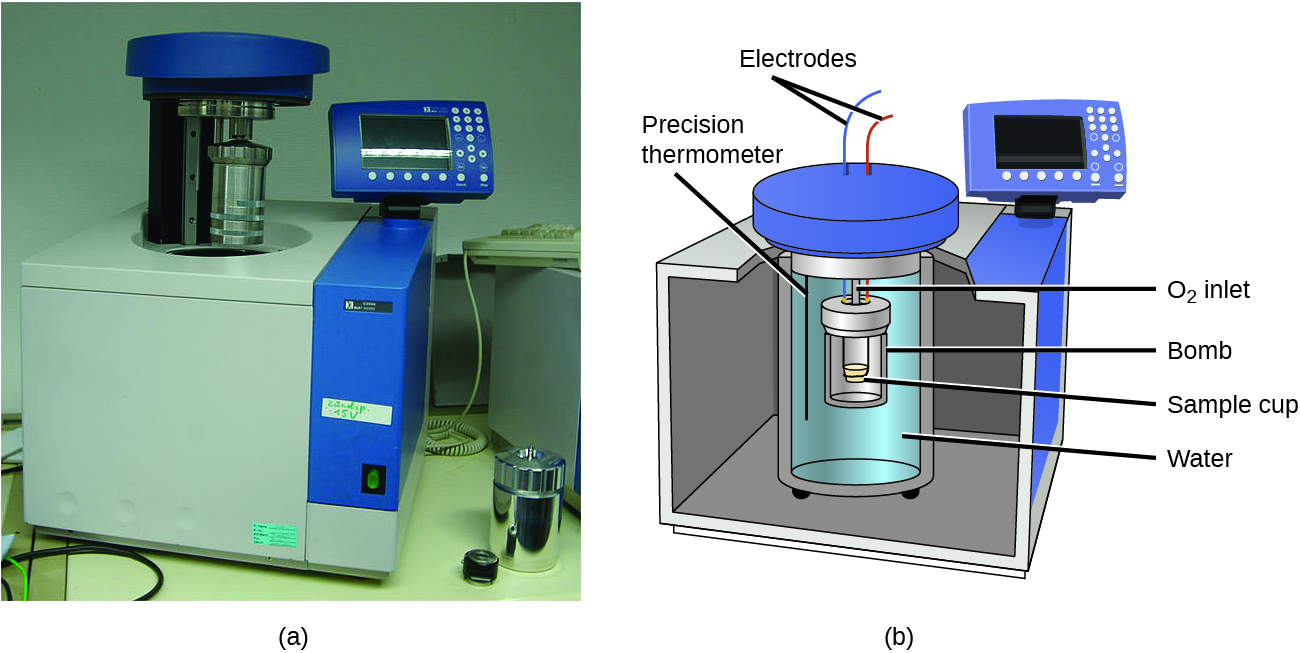
Click on this link to view how a bomb calorimeter is prepared for action.
This site shows calorimetric calculations using sample data.
Example 7
Bomb Calorimetry
When 3.12 g of glucose, C6H12O6, is burned in a bomb calorimeter, the temperature of the calorimeter increases from 23.8 °C to 35.6 °C. The calorimeter contains 775 g of water, and the bomb itself has a heat capacity of 893 J/°C. How much heat was produced by the combustion of the glucose sample?
Solution
The combustion produces heat that is primarily absorbed by the water and the bomb. (The amounts of heat absorbed by the reaction products and the unreacted excess oxygen are relatively small and dealing with them is beyond the scope of this text. We will neglect them in our calculations.)
The heat produced by the reaction is absorbed by the water and the bomb:
This reaction released 48.7 kJ of heat when 3.12 g of glucose was burned.
Check Your Learning
When 0.963 g of benzene, C6H6, is burned in a bomb calorimeter, the temperature of the calorimeter increases by 8.39 °C. The bomb has a heat capacity of 784 J/°C and is submerged in 925 g of water. How much heat was produced by the combustion of the glucose sample?
Answer:
39.0 kJ
Since the first one was constructed in 1899, 35 calorimeters have been built to measure the heat produced by a living person. These whole-body calorimeters of various designs are large enough to hold an individual human being. More recently, whole-room calorimeters allow for relatively normal activities to be performed, and these calorimeters generate data that more closely reflect the real world. These calorimeters are used to measure the metabolism of individuals under different environmental conditions, different dietary regimes, and with different health conditions, such as diabetes. In humans, metabolism is typically measured in Calories per day. A nutritional calorie (1 Calorie = 1 kcal) is the energy unit used to quantify the amount of energy derived from the metabolism of foods.
Measuring Nutritional Calories
In your day-to-day life, you may be more familiar with energy being given in Calories, or nutritional calories, which are used to quantify the amount of energy in foods. One calorie (cal) = exactly 4.184 joules, and one Calorie (note the capitalization) = 1000 cal, or 1 kcal. (This is approximately the amount of energy needed to heat 1 kg of water by 1 °C.)
The macronutrients in food are proteins, carbohydrates, and fats or oils. Proteins provide about 4 Calories per gram, carbohydrates also provide about 4 Calories per gram, and fats and oils provide about 9 Calories/g. Nutritional labels on food packages show the caloric content of one serving of the food, as well as the breakdown into Calories from each of the three macronutrients (Figure 14).
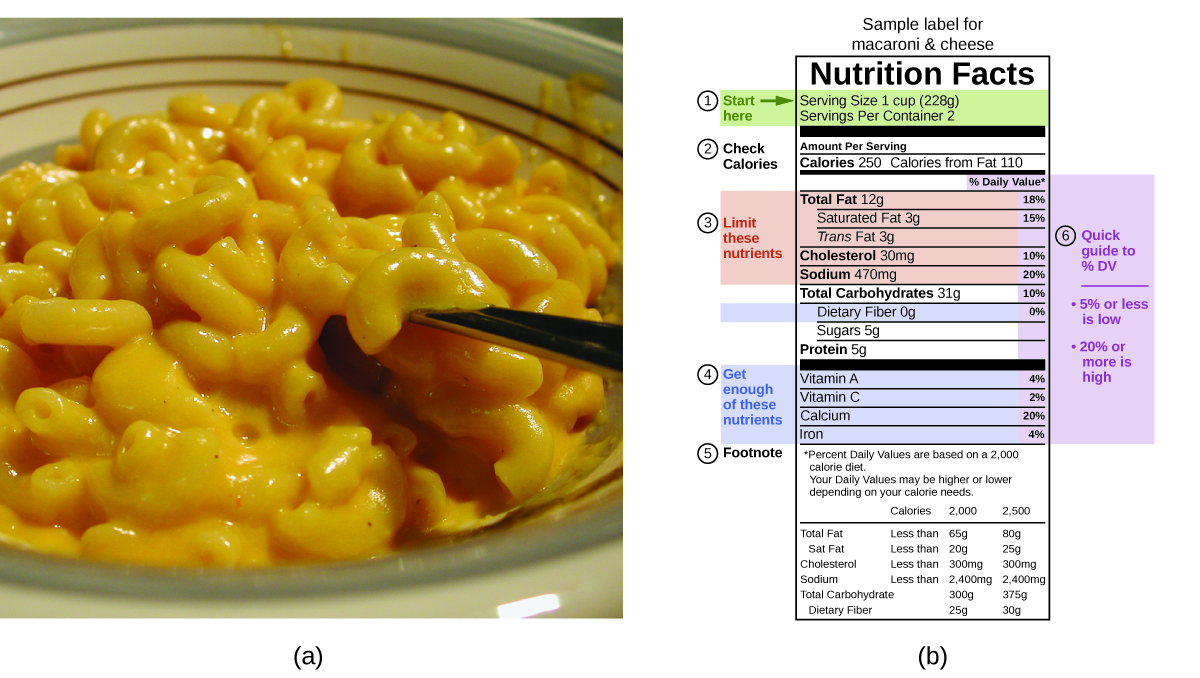
For the example shown in (b), the total energy per 228-g portion is calculated by:
So, you can use food labels to count your Calories. But where do the values come from? And how accurate are they? The caloric content of foods can be determined by using bomb calorimetry; that is, by burning the food and measuring the energy it contains. A sample of food is weighed, mixed in a blender, freeze-dried, ground into powder, and formed into a pellet. The pellet is burned inside a bomb calorimeter, and the measured temperature change is converted into energy per gram of food.
Today, the caloric content on food labels is derived using a method called the Atwater system that uses the average caloric content of the different chemical constituents of food, protein, carbohydrate, and fats. The average amounts are those given in the equation and are derived from the various results given by bomb calorimetry of whole foods. The carbohydrate amount is discounted a certain amount for the fiber content, which is indigestible carbohydrate. To determine the energy content of a food, the quantities of carbohydrate, protein, and fat are each multiplied by the average Calories per gram for each and the products summed to obtain the total energy.
Click on this link to access the US Department of Agriculture (USDA) National Nutrient Database, containing nutritional information on over 8000 foods.
Ch11.3 Enthalpy
Chemical thermodynamics is the science that deals with the relationships between heat, work, and other forms of energy in the context of chemical and physical processes.
Substances act as reservoirs of energy, meaning that energy can be added to them or removed from them. Energy is stored in a substance when the kinetic energy of its atoms or molecules is raised. The greater kinetic energy may be in the form of increased translations (travel or straight-line motions), vibrations, or rotations of the atoms or molecules. When thermal energy is lost, the intensities of these motions decrease and the kinetic energy decreases. The total of all possible kinds of energy present in a substance is called the internal energy (U), sometimes symbolized as E.
As a system undergoes a change, its internal energy can change, and energy can be transferred from the system to the surroundings, or vice versa. Energy is transferred into a system when it absorbs heat (q) from the surroundings or when the surroundings do work (w) on the system. For example, energy is transferred into room-temperature metal wire if it is immersed in hot water (the wire absorbs heat from the water), or if you rapidly bend the wire back and forth (the wire becomes warmer because of the work done on it). Both processes increase the internal energy of the wire, which is reflected in an increase in the wire’s temperature. Conversely, energy is transferred out of a system when heat is lost from the system, or when the system does work on the surroundings.
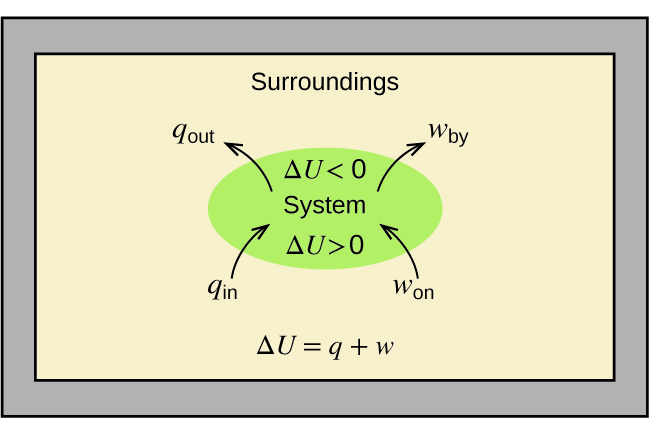
The relationship between internal energy, heat, and work can be represented by the equation (Figure 15):
This is one version of the first law of thermodynamics, and it shows that the internal energy of a system changes through heat flow into or out of the system (positive q is heat flow in; negative q is heat flow out) or work done on or by the system. The work, w, is positive if it is done on the system and negative if it is done by the system.
A type of work called expansion work (or pressure-volume work) occurs when a system pushes back the surroundings against a restraining pressure, or when the surroundings compress the system. An example of this occurs during the operation of an internal combustion engine. The reaction of gasoline and oxygen is exothermic. Some of this energy is given off as heat, and some does work pushing the piston in the cylinder. The substances involved in the reaction are the system, while the engine and the rest of the universe are the surroundings. The system loses energy by both heating and doing work on the surroundings, and its internal energy decreases. (The engine is able to keep the car moving because this process is repeated many times per second while the engine is running.)
This view of an internal combustion engine illustrates the conversion of energy produced by the exothermic combustion reaction of a fuel such as gasoline into energy of motion.
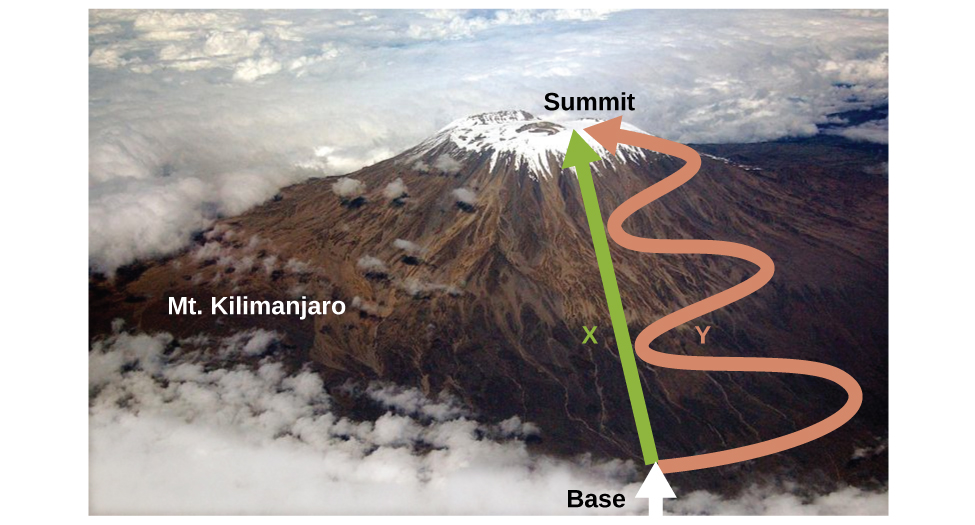
Internal energy is a type of quantity known as a state function (or state variable), whereas heat and work are not state functions. The value of a state function depends only on the state that a system is in, and not on how that state is reached. If a quantity is not a state function, then its value does depend on how the state is reached. An example of a state function is altitude or elevation. If you stand on the summit of Mt. Kilimanjaro, you are at an altitude of 5895 m, and it does not matter whether you hiked there or parachuted there. The distance you traveled to the top of Kilimanjaro, however, is not a state function. You could climb to the summit by a direct route or by a more roundabout, circuitous path (Figure 16).
Chemists ordinarily use a property known as enthalpy (H) to describe the thermodynamics of chemical and physical processes. Enthalpy is defined as the sum of a system’s internal energy (U) and the mathematical product of its pressure (P) and volume (V):
Since it is derived from three state functions (U, P, and V), enthalpy is also a state function. Enthalpy values for specific substances cannot be measured directly; only enthalpy changes for chemical or physical processes can be determined. For processes that take place at constant pressure (a common condition for many chemical and physical changes), the enthalpy change (ΔH) is:
The mathematical product PΔV represents work (w), namely, expansion or pressure-volume work. By their definitions, the arithmetic signs of ΔV and w will always be opposite:
Substituting yields:
where qp is the heat of reaction under constant pressure. Therefore, if a chemical or physical process is carried out at constant pressure with the only work done caused by expansion or contraction, then the heat flow (qp) equals enthalpy change (ΔH) for the process.
The heat given off when you operate a Bunsen burner is equal to the enthalpy change of the methane combustion reaction that takes place, since it occurs at the essentially constant pressure of the atmosphere. On the other hand, the heat produced by a reaction measured in a bomb calorimeter is not equal to ΔH because the closed, constant-volume metal container prevents expansion work from occurring. Chemists usually perform experiments under normal atmospheric conditions, at constant external pressure with q = ΔH, which makes enthalpy the most convenient choice for determining heat.
The following conventions apply when we use ΔH:
-
Chemists use a thermochemical equation to represent the changes in both matter and energy. In a thermochemical equation, the enthalpy change of a reaction is shown as a ΔH value following the equation for the reaction. This ΔH value indicates the amount of heat associated with the reaction involving the number of moles of reactants and products as shown in the chemical equation. For example:
[latex]\text{H}_2(g) + \frac{1}{2} \text{O}_2(g) \longrightarrow \text{H}_2 \text{O} (l) \;\; \Delta H = -286 \;\text{kJ}[/latex]which indicates that when 1 mole of hydrogen gas and [latex]\frac{1}{2}[/latex] mole of oxygen gas at some temperature and pressure change to 1 mole of liquid water at the same temperature and pressure, 286 kJ of heat are released to the surroundings. If the coefficients of the chemical equation are multiplied by some factor, ΔH must be multiplied by that same factor (ΔH is an extensive property):
[latex]\begin{array}{l l} (\text{two-fold increase in amounts}) \\ 2 \text{H}_2(g) + \text{O}_2(g) \longrightarrow 2 \text{H}_2 \text{O}(l) & \Delta H = 2 \times (-286 \;\text{kJ}) = -572 \;\text{kJ} \\[1em] (\text{two-fold decrease in amounts}) \\ \frac{1}{2} \text{H}_2(g) + \frac{1}{4} \text{O}_2(g) \longrightarrow \frac{1}{2} \text{H}_2 \text{O}(l) & \Delta H = \frac{1}{2} \times (-286 \;\text{kJ}) = -143 \;\text{kJ} \end{array}[/latex] -
ΔH of a reaction depends on the physical state of the reactants and products of the reaction (whether we have gases, liquids, solids, or aqueous solutions), so these must be shown. For example, when 1 mole of hydrogen gas and [latex]\frac{1}{2}[/latex] mole of oxygen gas change to 1 mole of gaseous water at the same temperature and pressure, only 242 kJ of heat are released.
[latex]\text{H}_2(g) + \frac{1}{2} \text{O}_2(g) \longrightarrow \text{H}_2 \text{O}(g) \;\;\;\;\; \Delta H = -242 \;\text{kJ}[/latex] -
A negative value of ΔH indicates an exothermic reaction; a positive value of ΔH indicates an endothermic reaction. If the direction of a chemical equation is reversed, the arithmetic sign of its ΔH is changed (a process that is endothermic in one direction is exothermic in the opposite direction).
Example 8
Measurement of an Enthalpy Change
When 0.0500 mol of HCl(aq) reacts with 0.0500 mol of NaOH(aq) to form 0.0500 mol of NaCl(aq), 2.9 kJ of heat are produced. What is ΔH, the enthalpy change, per mole of acid reacting?
Solution
For the reaction of 0.0500 mol acid (HCl), q = −2.9 kJ. This means:
Since that is the number of moles in the chemical equation, we write the thermochemical equation as:
Check Your Learning
When 1.34 g Zn(s) reacts with 60.0 mL of 0.750 M HCl(aq), 3.14 kJ of heat are produced. Determine the enthalpy change per mole of zinc reacting for the reaction:
Answer:
ΔH = −153 kJ per mol of Zn
Be sure to take both stoichiometry and limiting reactants into account when determining the ΔH for a chemical reaction.
Example 9
Another Example of the Measurement of an Enthalpy Change
A gummy bear contains 2.67 g sucrose, C12H22O11. When it reacts with 7.19 g potassium chlorate, KClO3, 43.7 kJ of heat are produced. Determine the enthalpy change for the reaction
Solution
We have:
[latex]7.19 \;\rule[0.5ex]{0.6em}{0.1ex}\hspace{-0.6em}\text{g} \times \frac{1 \;\text{mol}}{122.5 \;\rule[0.25ex]{0.55em}{0.1ex}\hspace{-0.55em}\text{g}} = 0.0587 \;\text{mol KClO}_3[/latex]
Since
C12H22O11 is the excess reactant and KClO3 is the limiting reactant.
The reaction uses 8 mol KClO3, so we have:
The thermochemical equation is:
Check Your Learning
When 1.42 g of iron reacts with 1.80 g of chlorine, 3.22 g of FeCl2(s) and 8.60 kJ of heat is produced. What is the enthalpy change for the reaction when 1 mole of FeCl2(s) is produced?
Answer:
ΔH = −339 kJ
Ch11.4 Hess’s Law
There are two ways to determine the amount of heat involved in a chemical change: measure it experimentally, or calculate it from other experimentally determined enthalpy changes. Some reactions are difficult, if not impossible, to investigate and make accurate measurements. And even when a reaction is not hard to perform or measure, it is convenient to be able to determine the heat involved in a reaction without having to perform an experiment.
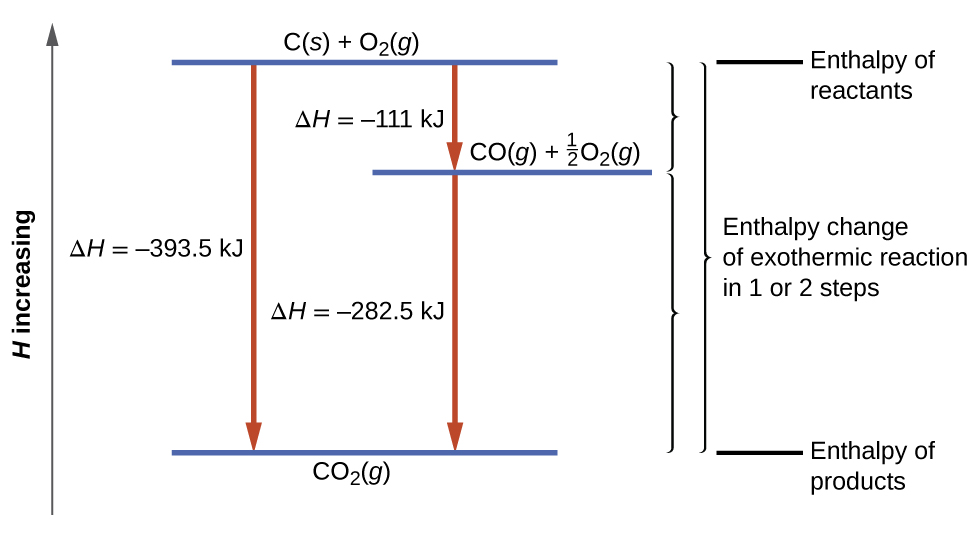
This type of calculation usually involves the use of Hess’s law, which states: If a process can be written as the sum of several stepwise processes, the enthalpy change of the total process equals the sum of the enthalpy changes of the various steps. Hess’s law is valid because enthalpy is a state function: Enthalpy changes depend only on where a chemical process starts and ends, but not on the path it takes from start to finish. For example, we can think of the reaction of carbon with oxygen to form carbon dioxide as occurring either directly:
or in a two-step process:
[latex]\text{CO}(g) + \frac{1}{2} \text{O}_2 (g) \longrightarrow \text{CO}_2(g) \;\;\;\;\; \Delta H = -283 \;\text{kJ}[/latex]
According to Hess’s law, the enthalpy change of the reaction will equal the sum of the enthalpy changes of the steps. We can find the enthalpy change of the entire reaction from its two steps:
The application of Hess's law is illustrated in Figure 17. This finding (overall ΔH for the reaction = sum of ΔH values for reaction “steps” in the overall reaction) is true in general for chemical and physical processes.
Example 10
Stepwise Calculation of [latex]\Delta H[/latex] Using Hess’s Law
Determine the enthalpy of the reaction
from the enthalpy changes of the following two-step process:
Solution
We see that the reaction for which we want to find ΔH is the sum of the two reactions with known ΔH values, so to sum:
Check Your Learning
Calculate ΔH for the process:
from the following information:
Answer:
66.4 kJ
Here is a less straightforward example that illustrates the thought process involved in solving many Hess’s law problems.
Example 11
A More Challenging Problem Using Hess’s Law
Chlorine monofluoride can react with fluorine to form chlorine trifluoride:
(i) [latex]\text{ClF}(g) + \text{F}_2(g) \longrightarrow \text{ClF}_3(g) \;\;\;\;\; \Delta H = ?[/latex]
Use the reactions here to determine the ΔH for reaction (i):
(ii) [latex]2\text{OF}_2(g) \longrightarrow \text{O}_2(g) + 2\text{F}_2(g) \;\;\;\;\; \Delta H_{(ii)} = -49.4 \;\text{kJ}[/latex]
(iii) [latex]2\text{ClF}(g) + \text{O}_2(g) \longrightarrow \text{Cl}_2 \text{O}(g) + \text{OF}_2(g) \;\;\;\;\; \Delta H_{(iii)} = +205.6 \;\text{kJ}[/latex]
(iv) [latex]\text{ClF}_3(g) + \text{O}_2(g) \longrightarrow \frac{1}{2}\text{Cl}_2 \text{O}(g) + \frac{3}{2} \text{OF}_2(g) \;\;\;\;\; \Delta H_{(iv)} = +266.7 \;\text{kJ}[/latex]
Solution
Our goal is to manipulate and combine reactions (ii), (iii), and (iv) such that they add up to reaction (i). Going from left to right in (i), we first see that ClF(g) is needed as a reactant. This can be obtained by multiplying reaction (iii) by [latex]\frac{1}{2}[/latex], which means that the ΔH is also multiplied by [latex]\frac{1}{2}[/latex]:
Next, we see that F2 is also needed as a reactant. To get this, reverse and halve reaction (ii), which means that the ΔH° changes sign and is halved:
To get ClF3 as a product, reverse (iv), changing the sign of ΔH°:
Now check to make sure that these reactions add up to the reaction we want:
Reactants [latex]\frac{1}{2} \text{O}_2[/latex] and [latex]\frac{1}{2} \text{O}_2[/latex] cancel out product O2; product [latex]\frac{1}{2} \text{Cl}_2 \text{O}[/latex] cancels reactant [latex]\frac{1}{2} \text{Cl}_2 \text{O}[/latex]; and reactant [latex]\frac{3}{2} \text{OF}_2[/latex] is cancelled by products [latex]\frac{1}{2} \text{OF}_2[/latex] and OF2. This leaves only reactants ClF(g) and F2(g) and product ClF3(g), which are what we want. Since summing these three modified reactions yields the reaction of interest, summing the three modified ΔH values will give the desired ΔH:
Check Your Learning
Aluminum chloride can be formed from its elements:
(i) [latex]2 \text{Al}(s) + 3\text{Cl}_2(g) \longrightarrow 2\text{AlCl}_3(s) \;\;\;\;\; \Delta H = ?[/latex]
Use the reactions here to determine the ΔH° for reaction (i):
(ii) [latex]\text{HCl}(g) \longrightarrow \text{HCl}(aq) \;\;\;\;\; \Delta H_{(ii)} = -74.8 \;\text{kJ}[/latex]
(iii) [latex]\text{H}_2(g) + \text{Cl}_2(g) \longrightarrow 2\text{HCl}(g) \;\;\;\;\; \Delta H_{(iii)} = -185 \;\text{kJ}[/latex]
(iv) [latex]\text{AlCl}_3(aq) \longrightarrow \text{AlCl}_3(s) \;\;\;\;\; \Delta H_{(iv)} = +323 \;\text{kJ/mol}[/latex]
(v) [latex]2\text{Al}(s) + 6\text{HCl}(aq) \longrightarrow 2\text{AlCl}_3(aq) + 3\text{H}_2 (g) \;\;\;\;\; \Delta H_{(v)} = -1049 \;\text{kJ}[/latex]
Answer:
−1407 kJ
Ch11.5 Standard State
Enthalpy changes are typically tabulated for reactions in which both the reactants and products are at the same conditions. A standard state is a commonly accepted set of conditions used as a reference point for the determination of properties under other different conditions. For chemists, the IUPAC standard state refers to materials under a pressure of 1 bar and solutions at 1 M, and does not specify a temperature. Many thermochemical tables list values with a standard state of 1 atm. Because the ΔH of a reaction changes very little with such small changes in pressure (1 bar = 0.987 atm), ΔH values (except for the most precisely measured values) are essentially the same under both sets of standard conditions. We will include a superscript “º” in the enthalpy change symbol to designate standard state. Since the usual (but not technically standard) temperature is 298.15 K, we will use a subscripted “298” to designate this temperature. Thus, the symbol ([latex]{\Delta}H^{\circ}_{298}[/latex]) is used to indicate an enthalpy change for a process occurring under these conditions. (The symbol ΔH is used to indicate an enthalpy change for a reaction occurring under nonstandard conditions.)
The enthalpy changes for many types of chemical and physical processes are available in the reference literature, including those for combustion reactions, phase transitions, and formation reactions. As we discuss these quantities, it is important to pay attention to the extensive nature of enthalpy and enthalpy changes. Since the enthalpy change for a given reaction is proportional to the amounts of substances involved, it may be reported on that basis (i.e., as the ΔH for specific amounts of reactants). However, we often find it more useful to divide one extensive property (ΔH) by another (amount of substance), and report a per-amount intensive value of ΔH, often “normalized” to a per-mole basis. (Note that this is similar to determining the intensive property specific heat from the extensive property heat capacity.)
Ch11.6 Standard Enthalpy of Formation
A standard enthalpy of formation [latex]\Delta H^\circ_\text{f}[/latex] is an enthalpy change for a reaction in which exactly 1 mole of a pure substance is formed from free elements in their most stable states under standard state conditions. These values are especially useful for computing or predicting enthalpy changes for chemical reactions that are impractical or dangerous to carry out, or for processes for which it is difficult to make measurements. If we have values for the appropriate standard enthalpies of formation, we can determine the enthalpy change for any reaction using Hess’s law.
The standard enthalpy of formation of CO2(g) is −393.5 kJ/mol. This is the enthalpy change for the exothermic reaction:
starting with the reactants at a pressure of 1 bar and 25 °C (with the carbon present as graphite, the most stable form of carbon under these conditions) and ending with one mole of CO2, also at 1 bar and 25 °C.
For nitrogen dioxide, NO2(g), [latex]\Delta H^\circ_\text{f}[/latex] is 33.2 kJ/mol. This is the enthalpy change for the reaction:
A reaction equation with [latex]\frac{1}{2}[/latex] mole of N2 and 1 mole of O2 is correct in this case because the standard enthalpy of formation always refers to 1 mole of product, NO2(g).
By definition, the standard enthalpy of formation of an element in its most stable form is equal to zero under standard conditions, which is 1 bar for gases and 1 M for solutions. You can find a table of standard enthalpies of formation of many common substances in the Appendix.
Example 12
Evaluating an Enthalpy of Formation
Ozone, O3(g), forms from oxygen, O2(g), by an endothermic process. Ultraviolet radiation is the source of the energy that drives this reaction in the upper atmosphere. Assuming that both the reactants and products of the reaction are in their standard states, determine the standard enthalpy of formation, [latex]\Delta H^{\circ}_\text{f}[/latex] of ozone from the following information:
Solution
[latex]\Delta H^\circ_\text{f}[/latex] is the enthalpy change for the formation of one mole of a substance in its standard state from the elements in their standard states. Thus, [latex]\Delta H^\circ_\text{f}[/latex] for O3(g) is the enthalpy change for the reaction:
For the formation of 2 mol of O3(g), [latex]\Delta H^\circ_{298} = +286 \;\text{kJ}[/latex]. Hence:
Therefore, [latex]\Delta H^\circ_\text{f} [\text{O}_3(g)] = +143 \;\text{kJ/mol}[/latex].
Check Your Learning
Hydrogen gas, H2, reacts explosively with gaseous chlorine, Cl2, to form hydrogen chloride, HCl(g). What is the enthalpy change for the reaction of 1 mole of H2(g) with 1 mole of Cl2(g) if both the reactants and products are at standard state conditions? The standard enthalpy of formation of HCl(g) is −92.3 kJ/mol.
Answer:
For the reaction [latex]\text{H}_2(g) + \text{Cl}_2(g) \longrightarrow 2\text{HCl}(g) \;\;\;\;\; \Delta H^\circ_{298} = -184.6 \;\text{kJ}[/latex]
Example 13
Writing Reaction Equations for [latex]\Delta H^\circ_\text{f}[/latex]
Write the heat of formation reaction equations for:
(a) C2H5OH(l)
(b) Ca3(PO4)2(s)
Solution
Remembering that [latex]\Delta H^\circ_\text{f}[/latex] reaction equations are for forming 1 mole of the compound from its constituent elements under standard conditions, we have:
(a) [latex]2\text{C}(s, \;\text{graphite}) + 3\text{H}_2(g) + \frac{1}{2} \text{O}_2(g) \longrightarrow \text{C}_2 \text{H}_5 \text{OH}(l)[/latex]
(b) [latex]3\text{Ca}(s) + \frac{1}{2} \text{P}_4(s) + 4\text{O}_2(g) \longrightarrow \text{Ca}_3 (\text{PO}_4)_2(s)[/latex]
Note: The standard state of carbon is graphite, and phosphorus exists as P4.
Check Your Learning
Write the heat of formation reaction equations for:
(a) C2H5OC2H5(l)
(b) Na2CO3(s)
Answer:
(a) [latex]4\text{C}(s, \;\text{graphite}) + 5\text{H}_2(g) + \frac{1}{2} \text{O}_2(g) \longrightarrow \text{C}_2 \text{H}_5 \text{O} \text{C}_2 \text{H}_5(l)[/latex];
(b) [latex]2\text{Na}(s) + \text{C}(s, \;\text{graphite}) + \frac{3}{2} \text{O}_2(s) \longrightarrow \text{Na}_2 \text{CO}_3(s)[/latex]
We also can use Hess’s law to determine the enthalpy change of any reaction if the corresponding enthalpies of formation of the reactants and products are available. The stepwise reactions we consider are: (i) decompositions of the reactants into their component elements (for which the enthalpy changes are proportional to the negative of the enthalpies of formation of the reactants), followed by (ii) re-combinations of the elements to give the products (with the enthalpy changes proportional to the enthalpies of formation of the products). The standard enthalpy change of the overall reaction is therefore equal to: (ii) the sum of the standard enthalpies of formation of all the products plus (i) the sum of the negatives of the standard enthalpies of formation of all the reactants. This is usually rearranged slightly to be written as follows (n is the stoichiometric coefficients):
The following example shows in detail why this equation is valid, and how to use it to calculate the enthalpy change for a reaction of interest.
Example 14
Using Hess’s Law
What is the standard enthalpy change for the reaction:
Solution:
Using the Equation:
Supporting Why the General Equation Is Valid
Alternatively, we can write this reaction as the sum of the decompositions of 3NO2(g) and 1H2O(l) into their constituent elements, and the formation of 2HNO3(aq) and 1NO(g) from their constituent elements. Writing out these reactions, and noting their relationships to the [latex]\Delta H^{\circ}_\text{f}[/latex] values for these compounds, we have:
Summing these reaction equations gives the reaction we are interested in:
Summing their enthalpy changes gives the value we want to determine:
So the standard enthalpy change for this reaction is ΔH° = −138.4 kJ.
Note that this result was obtained by (1) multiplying the [latex]\Delta H^{\circ}_\text{f}[/latex] of each product by its stoichiometric coefficient and summing those values, (2) multiplying the [latex]\Delta H^{\circ}_\text{f}[/latex] of each reactant by its stoichiometric coefficient and summing those values, and then (3) subtracting the result found in (2) from the result found in (1). This is also the procedure in using the general equation, as shown.
Check Your Learning
Calculate the heat of combustion of 1 mole of ethanol, C2H5OH(l), when H2O(l) and CO2(g) are formed.
C2H5OH(l) + 3O2(g) → 3H2O(l) + 2CO2(g)
Answer:
−1367 kJ/mol

