Unit Two
Day 10: Bond Properties
As you work through this section, if you find that you need a bit more background material to help you understand the topics at hand, you can consult "Chemistry: The Molecular Science" (5th ed. Moore and Stanitski) Chapter 6-6 through 6-8 and Chapter 6-10, and/or Chapter 5.1-5.6 in the Additional Reading Materials section.
D10.1 Covalent Bonds: Bond Length and Bond Enthalpy
In D6.1, you learned that as two atoms approach each other, electrons are shared between the nuclei and energy decreases. Bond length is the distance between two atomic nuclei at the minimum in a graph of energy versus nuclear separation. For example, the bond length in a H2 molecule is 74 pm, as shown in Figure 1.
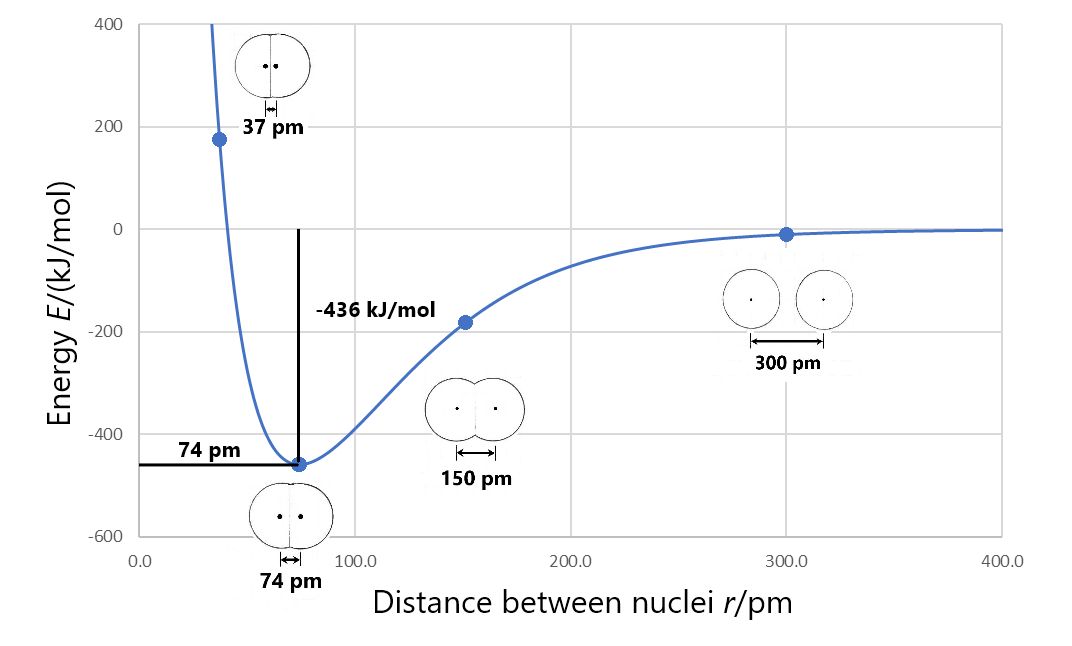
Bond enthalpy (also called bond energy) is the enthalpy change when the a chemical bond is broken; that is, when two bonded atoms are separated to a very large distance. For example, Figure 1 shows that the bonded hydrogen atoms have energy of −436 kJ/mol relative to the separated atoms. This means that the energy of the molecule must be increased by 436 kJ/mol to separate the atoms (break the bond) so the bond enthalpy for H2 is 436 kJ/mol.
Exercise 1: Bond Enthalpy
Bond lengths can be estimated by using the covalent radii (D5.1) of the bonded atoms. For example, if we add the covalent radius of C (77 pm) to that of O (74 pm), we obtain an estimate for the length of the C―O bond, 151 pm. (This is an estimate because covalent radii are averaged over many molecules and therefore are not exact for a specific molecule.) In general, the bigger the atoms are, the longer the bond between them will be.
Bond length also depends on bond order. For example, the N—O single bond length is 136 pm, but a N=O double bond is 115 pm long and a triple bond between N and O is 108 pm long.
You can find tables of average bond length and bond enthalpy in the appendix. Comparison of these two tables show a general trend where shorter bond lengths correspond to larger bond enthalpies.
Exercise 2: Bond Length and Atomic Radius
For each pair of bonds given below predict which bond is shorter. Use periodic-table trends in atomic radius and bond order to make your prediction.
D10.2 Reaction Enthalpy Change
The enthalpy change for a chemical reaction, ΔrH, is approximately equal to the sum of the enthalpies required to break each of the bonds in the reactant molecules (energy in, positive sign) plus the sum of the enthalpies released when each of the bonds in the product molecules forms (energy out, negative sign). This can be expressed mathematically:
ΔrH = ∑Ebonds broken - ∑Ebonds formed
Because the bond enthalpy values provided in the Appendix are averages over many different molecules for a type of bond, this calculation provides a rough estimate, not an exact value, for the enthalpy of reaction. It is also important that bond enthalpy calculations assume that all molecules are far from each other (which means that reactants and products must be in the gas phase). There would be additional enthalpy changes if the molecules came together and condensed to a liquid or formed a solid.
Consider this reaction, in which one H2 molecule and one Cl2 molecule react to form two HCl molecules:
H2(g) + Cl2(g) → 2HCl(g)
To form two H-Cl bonds (431 kJ/mol each), one H–H bond (436 kJ/mol) and one Cl–Cl bond (242 kJ/mol) are broken:
ΔrH = [EH-H + ECl-Cl] - 2EH-Cl = [436 kJ/mol + 242 kJ/mol] - 2(431 kJ/mol) = -184 kJ/mol
Because the bonds in the products are stronger than those in the reactants, the reaction has a net release of 184 kJ energy for every mole of reaction. The energy release increases the temperature of the surroundings (the reaction is exothermic). The experimental value for the quantity of energy released is 184.614 kJ/mol, slightly different from the value estimated using bond energies.
Based on bond enthalpy arguments, we can state general rules to predict qualitatively whether a chemical reaction releases energy (is exothermic):
- If there are more bonds in the product molecules than in the reactant molecules and the bonds have about the same strength, the reaction will be exothermic.
- If there are stronger bonds in the product molecules than in the reactant molecules and the number of bonds is the same in reactants and products, the reaction will be exothermic.
Example 1
Using Bond Energies to Calculate Approximate Enthalpy Changes
Methanol, CH3OH, may be an excellent alternative fuel. The high-temperature reaction of steam and carbon produces a mixture of the gases carbon monoxide, CO, and hydrogen, H2, from which methanol can be produced. Using the bond enthalpy table, calculate the approximate enthalpy change, ΔrH, for the reaction:
CO(g) + 2H2(g) → CH3OH(g)
Solution
First, consider the Lewis structures of the reactants and the products:
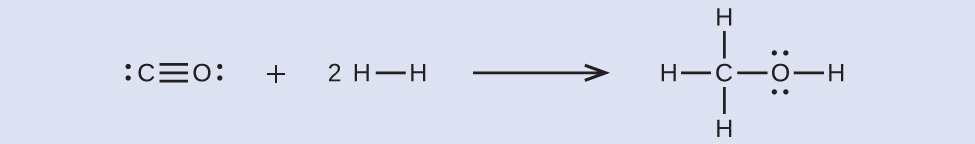
From this, we see that this reaction involves breaking a C≡O triple bond and two H–H single bonds, as well as forming three C–H single bonds, a C–O single bond, and an O–H single bond. We can express the enthalpy change as follows:
ΔrH = [EC≡O + 2(EH-H)] - [3(EC-H) + EC-O + EO-H]
Using the bond enthalpy values in the table, we obtain:
ΔrH = [1073 kJ/mol + 2(436 kJ/mol)] - [3(416 kJ/mol) + 336 kJ/mol + 467 kJ/mol] = -106 kJ/mol
Check Your Learning
Ethyl alcohol, CH3CH2OH, was one of the first organic chemicals deliberately synthesized by humans. It has many uses in industry, and it is the alcohol contained in alcoholic beverages. It can be obtained by the fermentation of sugar or synthesized by the hydration of ethylene in the following reaction:
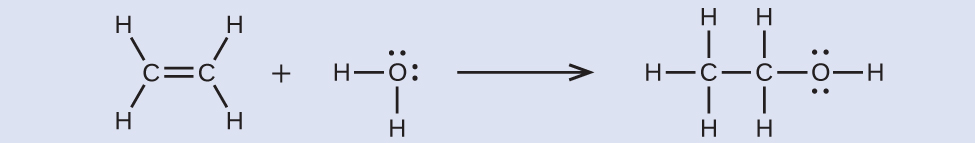
Using the bond enthalpy values, calculate an approximate enthalpy change, ΔrH, for this reaction.
Answer:
–43 kJ/mol
D10.3 Covalent Bonds: Bond Polarity
If the atoms that form a covalent bond are identical, as in H2 or Cl2, then the electrons in the bond must be shared equally. We refer to this as a pure covalent bond. Electrons shared in pure covalent bonds have an equal probability of being near each nucleus.
When different atoms are linked by a covalent bond, the bonding electrons can be more attracted by one atom than the other. This unequal distribution of bond electrons is known as a polar covalent bond. For example, in HCl, the Cl atom attracts the bond pair of electrons slightly more than does the H atom, and electron density of the H–Cl bond is shifted toward the chlorine atom. The chlorine atom, which has 17 protons, has electron density equivalent to 17.28 electrons and a partial negative charge, δ– = −0.28. The hydrogen atom has a partial positive charge, δ+ = +0.28.
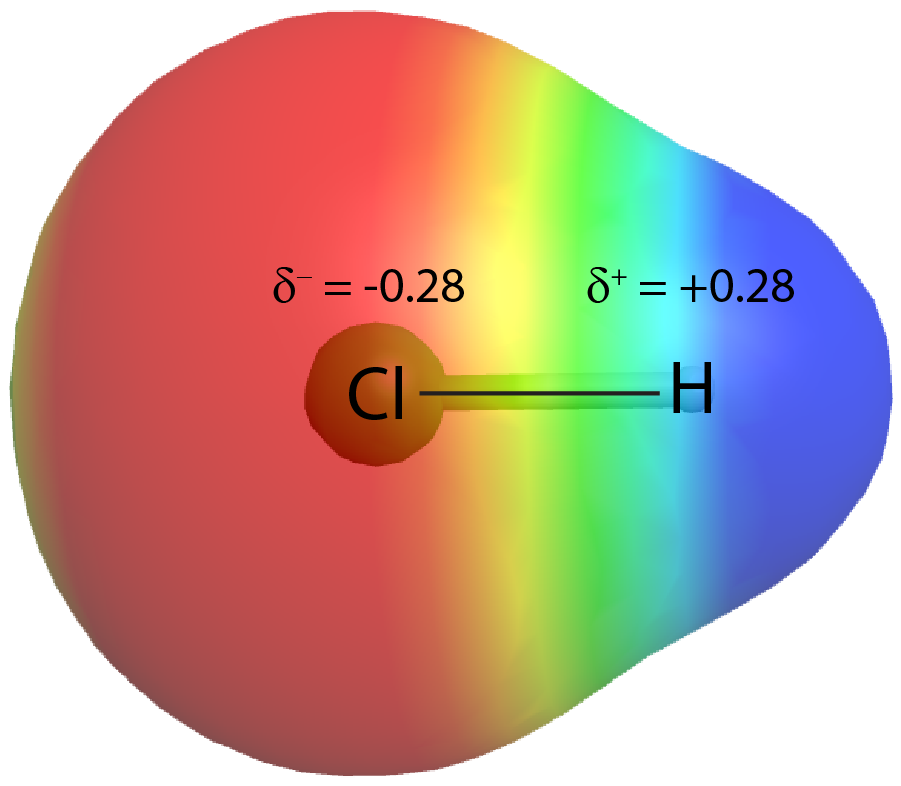
This unequal distribution of charge on two bonded atoms produces a bond dipole moment, the magnitude of which is represented by µ (Greek letter mu). The dipole moment is equal to:
μ = Qr
where Q is the magnitude of the partial charges (for HCl this is 0.28 times the charge of an electron) and r is the distance between the charges (the bond length).
The bond dipole moment has both direction and magnitude and can be represented as a vector. A dipole vector is shown as an arrow with a small + sign on the partially positive end and a point at the partially negative end. The length of the arrow is proportional to the dipole moment, µ.
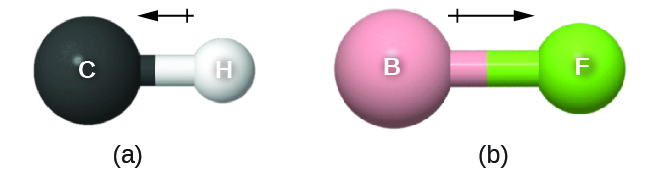
D10.4 Electronegativity
The polarity of a covalent bond is determined by the difference in electronegativity of the bonded atoms. Electronegativity (EN) is the tendency of an atom to attract bond electron density. Thus, the more electronegative atom in a bond is the one with the δ– charge. The greater the difference in electronegativity between two bonded atoms the more the electron density in the bond shifts toward the more electronegative atom and the larger the partial charges on the atoms are.
In general, electronegativity increases from left to right across a period in the periodic table and decreases down a group. Thus, elements in the upper right corner of the periodic table tend to have the highest electronegativities, with fluorine being the most electronegative element of all (EN = 4.0). (Note that we do not typically consider the EN values of noble gases because these atoms usually do not form molecules.) Also, it is hard to predict the electronegativity of hydrogen using the periodic table; based on its electronegativity of 2.1, H should be above and between B (1.9) and C(2.4), which is far from its typical location at the upper left corner.
Electronegativity values of most elements are tabulated in the appendix.
Electronegativity Differs from Electron Affinity
Electron affinity is an experimentally measurable physical quantity—the energy absorbed when an isolated gas-phase atom acquires an electron—usually expressed in kJ/mol. Electronegativity describes how strongly an atom attracts electrons in a bond. It is calculated, not measured, has an arbitrary relative scale, and has no units.
Electronegativity and Bond Type
The difference in electronegativity (ΔEN) of two bonded atoms provides a rough estimate of the bond polarity to be expected and, thus, the bond type. When ΔEN is very small (or zero), the bond is covalent and nonpolar. When it is large, the bond is polar covalent or ionic.
ΔEN spans a continuous scale and serves as a general guide; there is no definitive cutoff that defines a bond type. For example, HF has a ΔEN of 1.9 and is considered a polar covalent molecule, while NaCl has a ΔEN of 1.8 and forms an ionic compound. When considering the covalent or ionic character of a bond, you should also take into account the types of atoms involved and their relative positions in the periodic table. Bonds between two nonmetals are usually described as covalent; bonding between a metal and a nonmetal is often ionic.
Some compounds contain both covalent and ionic bonds. For example, potassium nitrate, KNO3, contains the K+ cation and the polyatomic NO3− anion.
Exercise 3: Polarity and Electronegativity Difference
Based on electronegativity alone, identify three elements that you expect would carry a partial negative charge when bonded to bromine.
Example 2
Electronegativity and Bond Polarity
Bond polarities play an important role in determining the structure of proteins. Using the electronegativity values provided in the Appendix, arrange these covalent bonds—all commonly found in amino acids—in order of increasing polarity. Then designate the positive and negative atoms using the symbols δ+ and δ–:
C–N, C–O, N–H, O–H, S–H
Solution
The polarity of these bonds increases as the absolute value of the electronegativity difference increases. The atom with the δ– designation is the more electronegative of the two.
| Bond | ΔEN | Polarity |
|---|---|---|
| S–H | 0.2 | [latex]\overset{\delta -}{\text{S}} - \overset{\delta +}{\text{H}}[/latex] |
| C–N | 0.6 | [latex]\overset{\delta +}{\text{C}} - \overset{\delta -}{\text{N}}[/latex] |
| N–H | 0.9 | [latex]\overset{\delta -}{\text{N}} - \overset{\delta +}{\text{H}}[/latex] |
| C–O | 1.0 | [latex]\overset{\delta +}{\text{C}} - \overset{\delta -}{\text{O}}[/latex] |
| O–H | 1.3 | [latex]\overset{\delta -}{\text{O}} - \overset{\delta +}{\text{H}}[/latex] |
Check Your Learning
Silicones are polymeric compounds containing, among others, the following types of covalent bonds: Si–O, Si–C, C–H, and C–C. Use electronegativity values to arrange the bonds in order of increasing polarity and designate the positive and negative atoms using the symbols δ+ and δ–.
Answer:
| Bond | Electronegativity Difference | Polarity |
|---|---|---|
| C–C | 0.0 | nonpolar |
| C–H | 0.3 | [latex]\overset{\delta -}{\text{C}} - \overset{\delta +}{\text{H}}[/latex] |
| Si–C | 0.8 | [latex]\overset{\delta +}{\text{Si}} - \overset{\delta -}{\text{C}}[/latex] |
| Si–O | 1.8 | [latex]\overset{\delta +}{\text{Si}} - \overset{\delta -}{\text{O}}[/latex] |
D10.5 Formal Charge
The formal charge of an atom in a molecule is the charge the atom would have if the electrons in the bonds are evenly distributed between the atoms. It is calculated by considering the number of valence electrons of an atom, and subtracting from it the number of nonbonding electrons and half the number of bonding electrons associated with that atom in the Lewis structure of the molecule:
formal charge = # valence electrons in an unbonded atom - # lone-pair electrons - 0.5(# bonding electrons)
The sum of the formal charges of all atoms in an uncharged molecule must be zero; the sum of the formal charges in an ion should equal the charge of the ion.
The formal charge calculated for an atom is not the actual charge of the atom in the molecule. Formal charge is only a useful bookkeeping tool; it does not correspond to the actual partial charges such as those calculated in Figure 2.
Exercise 4: Calculating Formal Charge
Calculate the formal charge on nitrogen in each of the following Lewis structures.
Example 3
Calculating Formal Charge from Lewis Structures
Assign formal charges to each atom in the interhalogen ion ICl4−.
Solution
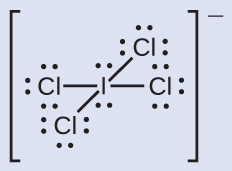
- We divide the bonding electron pairs equally for all I–Cl bonds:
- We assign lone pairs of electrons to their atoms.
- Each Cl atom now has seven electrons assigned to it, and the I atom has eight.
- Subtract this number from the number of valence electrons for the neutral atom:
- I: 7 – 8 = –1; Cl: 7 – 7 = 0. The sum of the formal charges of all the atoms equals –1, which is identical to the charge of the ion (–1).
Check Your Learning
Calculate the formal charge for each atom in the carbon monoxide molecule: ![]()
Answer:
C −1, O +1
Example 4
Calculating Formal Charge from Lewis Structures
Assign formal charges to each atom in the interhalogen molecule BrCl3.
Solution
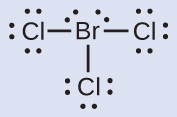
- Assign one of the electrons in each Br–Cl bond to the Br atom and one to the Cl atom in that bond:
- Assign the lone pairs to their atom.
- Now each Cl atom is assigned seven electrons and the Br atom is assigned seven electrons.
- Subtract this number from the number of valence electrons for the neutral atom.
- This gives the formal charge: Br: 7 – 7 = 0; Cl: 7 – 7 = 0. All atoms in BrCl3 have a formal charge of zero, and the sum of the formal charges totals zero, as it must be in a neutral molecule.
Check Your Learning
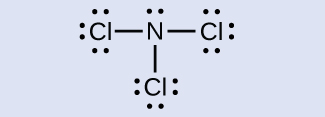
Determine the formal charge for each atom in NCl3.
Answer:
N: 0; all three Cl atoms: 0
Using Formal Charge to Predict Lewis Structure
In many cases, following the steps for writing Lewis structures may lead to more than one possible electron and/or atomic arrangement. Formal charge can be helpful in deciding which of the possible structures is most likely for a particular molecule:
- For an uncharged molecule a Lewis structure in which all formal charges are zero is preferable.
- The smaller the number of atoms with nonzero formal charges, the better.
- The smaller the magnitude of the formal charges, the better.
- A structure with formal charges of the same sign (both + or both −) on adjacent atoms is less stable.
- Structures with the negative formal charges on the more electronegative atoms are preferable.
For example, consider the following three possible Lewist structure of carbon dioxide, CO2:
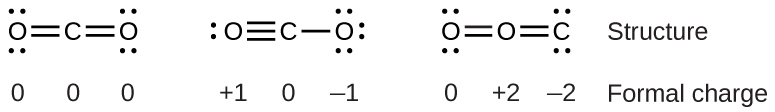
Comparing the three formal charges, we can identify the structure on the left as preferable because it has only formal charges of zero. the structure on the right is least likely because of the larger formal charges.
Exercise 5: Formal Charge and Lewis Structure
In the best Lewis structure for BeCl2, what is the formal charge on the beryllium atom?
Example 5
Using Formal Charge to Determine Molecular Structure
Nitrous oxide, N2O, commonly known as laughing gas, is used as an anesthetic in minor surgeries, such as the routine extraction of wisdom teeth. Which is the likely structure for nitrous oxide?
![]()
Solution
Determining formal charge yields the following:

The left structure with a terminal oxygen atom best satisfies the criteria for the most stable distribution of formal charge. The number of atoms with formal charges are minimized, and there is no formal charge larger than one. This is also consistent with the preference for having the less electronegative atom in the central position.
Check Your Learning
Which is the most likely molecular structure for the nitrite (NO2−) ion?
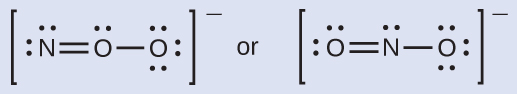
Answer:
ONO–
D10.6 Exceptions to the Octet Rule
Some covalent molecules have central atoms that do not have eight electrons in their Lewis structures. These molecules fall into three categories.
Odd-electron Molecules
A molecule that contains an odd number of electrons must have at least one electron unpaired. A molecule with at least one unpaired electron is called a free radical. Nitric oxide, NO, is an example; it is produced in internal combustion engines when oxygen and nitrogen react at high temperatures.
To draw the Lewis structure for an odd-electron molecule, follow the same six steps as for other molecules (section 7.3), but recognize that an odd-electron molecule will have less than an octet on some atom. For example, the Lewis structure for NO is:
![]()
Forming a triple bond would cause either oxygen or nitrogen to exceed an octet. Placing the unpaired electron on N makes sense because the formal charges are zero on both atoms in this structure. (Too verify that the structure above is better, calculate the formal charges on N and O if N had two lone pairs and O had a lone pair and an unpaired electron.)
Electron-deficient Molecules
A few molecules contain a central atom that does not have a filled valence shell. Usually, these central atoms are from groups 2 (IIA) and 13 (IIIA). For example, the Lewis structure of beryllium dihydride, BeH2, shows beryllium with only four electrons, and that of boron trifluoride, BF3, shows boron with only six electrons.
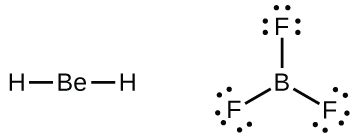
It is possible to draw a structure for BF3 with one B=F double bond, satisfying the octet rule, but experimental evidence tells us that the bond lengths are closer to that expected for B–F single bonds. (Such a structure would have a negative formal charge on B and a positive formal charge on the more electronegative F, which is not preferable.) The reactivity of BF3 is also consistent with an electron deficient boron. BF3 readily reacts with any molecule containing an atom with a lone pair of electrons. For example, NH3 reacts with BF3 with the lone pair on nitrogen (red) forming a bond (red) that completes the octet of the boron atom:
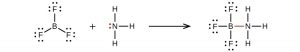
Hypervalent Molecules
Some Lewis structures show more than four pairs of electrons around the central atom. This usually happens when the central atom is in the third or a higher period (n ≥ 3). Molecules with more than an octet around the central atom are called hypervalent molecules. For example, in PCl5, the central phosphorus atom is surrounded by five pairs of electrons. In SF6, sulfur has six pairs of electrons.
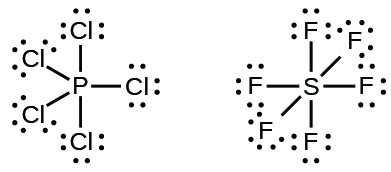
Example 6
Writing Lewis Structures: Octet Rule Violations
Xenon is a noble gas, but it forms a number of stable compounds. Write the Lewis structures of XeF2 and XeF6.
Solution
Follow the six steps in section 7.3. In this case, we condense the steps.
1. Calculate the number of valence electrons:
XeF2: 8 + (2 × 7) = 22
XeF6: 8 + (6 × 7) = 50
2 and 3. Draw a skeleton joining the atoms by single bonds. Xenon will be the central atom because fluorine can only form one bond:
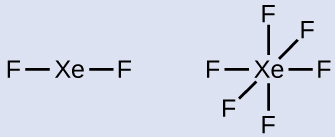
4 and 5. Distribute the remaining electrons.
![]()
XeF2: With an octet on each F, three lone pairs remain and are placed on the Xe. This is acceptable because Xe is in the fifth period (n = 5).
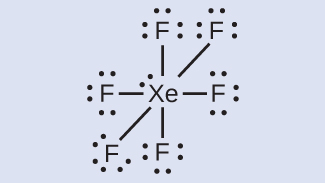
XeF6: With six bonds and three lone pairs of electrons around each F atom (36 electrons), two electrons remain. Place this lone pair on the Xe atom.
Check Your Learning
The halogens form a class of compounds called the interhalogens, in which halogen atoms covalently bond to each other. Write the Lewis structures for the interhalogens BrCl3 and ICl4−.
Answer:
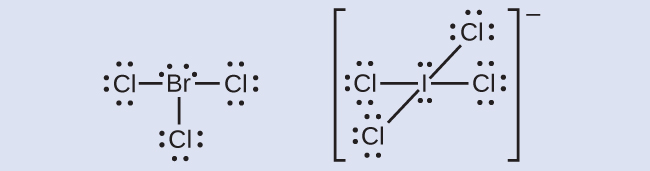
Podia Question
These two reactions occur when charcoal burns in a grill. The second reaction produces a poisonous gas, CO, which is the reason you should not use a charcoal grill indoors.
(1) C(s) + O2(g) → CO2(g)
(2) 2 C(s) + O2(g) → 2 CO(g)
Your goal is to predict which reaction releases more energy per gram of carbon.
Write down a plan for how to make that prediction. List steps in the plan and what information you would need to follow through with the plan.
Obtain the necessary information and carry out your plan. Which reaction releases more energy per gram of C(s)?
Two days before the next whole-class session, this Podia question will become live on Podia, where you can submit your answer.

