Unit Two
Day 18: Reaction Rate
As you work through this section, if you find that you need a bit more background material to help you understand the topics at hand, you can consult “Chemistry: The Molecular Science” (5th ed. Moore and Stanitski) Chapter 11-1 through 11-2, and/or Chapter 9.1-9.5 in the Additional Reading Materials section.
D18.1 Reaction Rate
The rate of a chemical reaction is usually defined as the change in concentration of a reactant or a product per unit time. Rates can be determined by measuring time from the start of reaction and either concentration or some property that can be related to concentration. For example, for reactions involving one or more colored substances, light absorption could be measured at different times after the start of the reaction.
Consider the decomposition reaction of cyclobutane to ethene in the gas phase:
The rate at which C4H8 decomposes can be expressed in terms of the rate of change of its concentration:
In this equation, square brackets represent concentration in mol/L so [C4H8]t1 represents the concentration of cyclobutane at time t1 and Δ[C4H8] represents the change in concentration of cyclobutane during the time interval Δt (that is, t2 − t1). The minus sign is in the equation because reaction rate is defined to be positive. The reactant concentration decreases as the reaction proceeds, making Δ[C4H8] a negative quantity, so a negative sign is needed to make it positive.
Table 1 provides an example of data collected during the decomposition of C4H8. (M represents the units mol/L.)
| Time (s) | [C4H8] (M) | Δ[C4H8] (M) | Δt (s) | Rate of decomposition (mol L−1 s−1) |
| 0.0 | 0.240 | |||
| 20.0 | 0.120 | -0.120 | 20.0 | 0.0060 |
| 40.0 | 0.060 | -0.060 | 20.0 | 0.0030 |
| 60.0 | 0.030 | -0.030 | 20.0 | 0.0015 |
| 80.0 | 0.015 | -0.015 | 20.0 | 0.0008 |
Notice that the reaction rate varies with time, decreasing as the reaction proceeds and the concentration of C4H8 decreases. Results for the first and last 20-second period are:
An average rate over a given time period can be calculated using the concentrations at the beginning and end of the period. The rate of reaction at any specific time is known as the instantaneous rate. The instantaneous rate at “time zero,” when the reaction starts, is the initial rate.
The instantaneous rate of a reaction may be determined one of two ways:
- If concentration changes can be measured over very short time intervals, then average rates over these very short time intervals provide reasonably good approximations of instantaneous rates.
- If we plot concentration vs. time, the instantaneous rate at any time t is given by the slope of a straight line that is tangent to the curve at that time (Figure 1).
![A graph is shown with the label, “Time (s ),” appearing on the x-axis and “delta [ C subscript 4 H subscript 8 ] ( mol L superscript negative 1)” on the y-axis. The x-axis markings begin at 0 and end at 100. The markings are labeled at intervals of 20. The y-axis begins at 0 and includes markings every 0.04, up to 0.24. A red, decreasing, concave up, non-linear curve is shown, which begins at 0.24 on the y-axis and nearly reaches a value of 0 at the far right of the graph around 100 on the x-axis. A black tangent line segment is drawn on the graph at the point where the graph intersects the y-axis. A second black tangent line segment is drawn near the middle of the curve. A vertical dashed line segment extends from the left endpoint of the line segment downward to intersect with a similar horizontal line segment drawn from the right endpoint of the line segment, forming a right triangle beneath the curve. The vertical leg of the triangle is labeled “capital delta [ C subscript 4 H subscript 8 ]” and the horizontal leg is labeled, “capital delta t.”](https://wisc.pb.unizin.org/app/uploads/sites/290/2019/03/Day18_Fig01-GraphWithLabels.jpg)
Exercise 1: Reaction Rates from Concentration Graph
Solution for part b and part c
D18.2 Relative Rates of Reaction
The rate of a reaction may be expressed in terms of the change in concentration of any reactant or product, and but depends on the stoichiometry of the reaction. Consider the ammonia decomposition reaction:
Because one nitrogen molecule is produced for every two ammonia molecules that react, the rate of formation of nitrogen is half the rate of disappearance of ammonia. Thus,
The negative sign accounts for the fact that the reactant concentration is decreasing while the product concentration is increasing. The fraction 1/2 accounts for the stoichiometry.
Similarly, because 3 mol H2 forms during the time required for formation of 1 mol N2,
Figure 2 plots concentrations vs. time for the reaction. At any time, the instantaneous rates for reactants and products are related by the reciprocals of their stoichiometric coefficients. For example, at 500 s the rate of hydrogen production three times greater than that for nitrogen production.
![A graph is shown with the label, “Time ( s ),” appearing on the x-axis and, “Concentration ( M ),” on the y-axis. The x-axis markings begin at 0 and end at 2000. The markings are labeled at intervals of 500. The y-axis begins at 0 and includes markings every 1.0 times 10 superscript negative 3, up to 4.0 times 10 superscript negative 3. A decreasing, concave up, non-linear curve is shown, which begins at about 2.8 times 10 superscript negative 3 on the y-axis and nearly reaches a value of 0 at the far right of the graph at the 2000 marking on the x-axis. This curve is labeled, “[ N H subscript 3].” Two additional curves that are increasing and concave down are shown, both beginning at the origin. The lower of these two curves is labeled, “[ N subscript 2 ].” It reaches a value of approximately 1.25 times 10 superscript negative 3 at 2000 seconds. The final curve is labeled, “[ H subscript 2 ].” It reaches a value of about 3.9 times 10 superscript negative 3 at 2000 seconds. A red tangent line segment is drawn to each of the curves on the graph at 500 seconds. At 500 seconds on the x-axis, a vertical dashed line is shown. Next to the [ N H subscript 3] graph appears the equation “negative capital delta [ N H subscript 3 ] over capital delta t = negative slope = 1.94 times 10 superscript negative 6 M / s.” Next to the [ N subscript 2] graph appears the equation “negative capital delta [ N subscript 2 ] over capital delta t = negative slope = 9.70 times 10 superscript negative 7 M / s.” Next to the [ H subscript 2 ] graph appears the equation “negative capital delta [ H subscript 2 ] over capital delta t = negative slope = 2.91 times 10 superscript negative 6 M / s.”](https://wisc.pb.unizin.org/app/uploads/sites/126/2017/08/CNX_Chem_12_01_NH3Decomp.jpg)
Thus, the rate of reaction is defined by taking the change in concentration of a reactant or product and multiplying by the reciprocal of the stoichiometric coefficient for each reactant or product. For a reactant the stoichiometric coefficient is given a negative sign (because the concentration is decreasing and rates are defined to be positive). For the reaction aA + bB → cC + dD, where lower-case letters are coefficients and upper-case letters represent chemical formulas,
![]()
Example 1
Expressions for Relative Reaction Rates
The first step in the production of nitric acid is the combustion of ammonia:
Write the equations that relate the rates of consumption of the reactants and the rates of formation of the products.
Solution
Considering the stoichiometry of this homogeneous reaction, the rates for the consumption of reactants and formation of products are:
Check Your Learning
In a reaction described by the following net ionic equation:
Write the equations that relate the rates of consumption of the reactants and the rates of formation of the products.
Answer:
Example 2
Reaction Rate Expressions for Decomposition of H2O2
Consider the decomposition of H2O2:
The instantaneous rate of decomposition of H2O2 at t = 11.1 h is determined to be 3.20 × 10−2 M/h. Calculate the instantaneous rate of production of H2O and O2 at t = 11.1 h.
Solution
Using the stoichiometry of the reaction,
Therefore:
and
Check Your Learning
If the rate of decomposition of ammonia, NH3, at 1150 K is 2.10 × 10−6 M/s, what is the rate of production of nitrogen and hydrogen?
Answer:
1.05 × 10−6 M/s for N2 and 3.15 × 10−6 M/s for H2.
Exercise 2: Reaction Rate and Stoichiometry
Measurements of the concentration of iodide ([I-]) are made to measure the kinetics of the following reaction:
Suppose the concentration of iodide decreased by 1.0 × 10-3 M over the course of the first 10 seconds of the reaction. Assuming that only reactants were present at the start of the reaction, what concentration of sulfate ions (SO42-) would you expect to be present after the first 10 seconds of the reaction?
D18.3 Factors Affecting Reaction Rates
When a chemical reaction occurs, one or more reactant substances are changed into one or more product substances. This involves changes in bonding, which requires that atoms, molecules, or ions be in close contact; that is, atomic-scale particles must collide to react. Anything that affects the number and/or effectiveness of those collisions will affect the rate of reaction.
Chemical Nature of the Reacting Substances
Some substances react faster than others. Different substances have different atomic-scale structures and different bonding. For example, calcium and sodium both react with water to form hydrogen gas and a basic solution. Yet calcium reacts at a moderate rate, whereas sodium reacts so rapidly that the reaction is almost explosive. The reaction involves loss of electrons from sodium or calcium atoms, and sodium has a smaller first ionization energy.
Temperature of the Reaction
Chemical reactions typically occur faster at higher temperatures. At higher temperatures atomic-scale particles move faster, so they collide harder and more often, both of which increase the probability that they will react. For example, natural gas (CH4) does not react rapidly with air at room temperature, but strike a match and BOOM!
Concentrations
Rates usually increase when the concentration of one or more of the reactants increases. In some cases, rates depend on the concentrations of products as well. For example, calcium carbonate (CaCO3) deteriorates as a result of its reaction with the pollutant sulfur dioxide. The rate of this reaction depends on the concentration of sulfur dioxide in the air. Sulfur dioxide reacts with water vapor to produce sulfurous acid,
Sulfurous acid then reacts with calcium carbonate,
In a more polluted atmosphere where the concentration of sulfur dioxide is higher, calcium carbonate deteriorates more rapidly (Figure 4).

Presence and Concentration of a Catalyst
A catalyst is a substance that increases the rate of a chemical reaction by providing an alternative reaction pathway but is not consumed by the reaction. The greater the concentration of a catalyst the more the catalyst can speed up a reaction. How catalysts work will be discussed in detail later.
Surface Area
The factors discussed so far apply to homogeneous reactions, reactions that occur in a single phase (solid, liquid, or gas). If a reaction occurs at a surface, the intersection of two phases (such as the surface of a solid in contact with a gas), an increase in surface area can increase the rate. Reactions that take place at a surface are called heterogeneous reactions. A finely divided solid has more surface area available for reaction than does one large piece of the same substance. For example, large pieces of iron can be held in a burner flame for a long time and hardly react whereas iron powder blown into the flame sparkles as the tiny particles burn. (Click here for a video.) Large pieces of wood smolder, smaller pieces burn rapidly, and sawdust burns explosively.
D18.4 Effect of Concentration: Rate Laws
Rate laws or rate equations are mathematical expressions that relate the rate of a chemical reaction to the concentrations of reactants (and sometimes products or catalysts). Often the rate of reaction is proportional to concentration, or to a power of a concentration, of a substance involved in the reaction:
Here, [A], [B], and [C] represent concentrations, k is the rate constant, and each exponent, m, n, and p, defines the reaction order with respect to each reactant. The rate constant is a proportionality constant independent of reactant concentrations and specific for a particular reaction at a particular temperature. The order of a reaction is the power to which a concentration must be raised to correctly calculate the rate. For example, if m = 1, the reaction is first-order with respect to A; if n = 2, the reaction is second-order with respect to B; if p = 0, the reaction is zeroth-order with respect to C, which means that the rate of the reaction is not affected by the concentration of C because [C]0 = 1. The overall reaction order is the sum of the individual orders, m + n + p + … Reaction orders are usually positive integers, although they can be fractions or negative numbers.
Example 3
Writing Rate Laws from Reaction Orders
An experiment shows that the reaction of nitrogen dioxide with carbon monoxide:
is second-order in NO2 and zeroth-order in CO at 100 °C. What is the rate law for the reaction?
Solution
The rate law has the form,
The reaction is second-order in NO2; thus m = 2. The reaction is zeroth-order in CO; thus n = 0. The rate law is:
The rate of reaction is solely dependent on the concentration of NO2. When we consider reaction mechanisms, we will explain how a reactant’s concentration can have no effect on reaction rate.
Check Your Learning
The rate law for the reaction:
has been determined to be rate = k[NO]2[H2]. What are the orders with respect to each reactant, and what is the overall order of the reaction?
Answer:
Second-order in NO; first-order in H2; third-order overall
Check Your Learning
In a transesterification reaction, a triglyceride reacts with an alcohol to form an ester and glycerol. Many students learn about the reaction between methanol (CH3OH) and ethyl acetate (CH3CH2OCOCH3) as a sample reaction before studying the chemical reactions that produce biodiesel:
The rate law for this reaction, under certain conditions, is determined to be:
What is the order of reaction with respect to methanol and ethyl acetate, and what is the overall order of reaction?
Answer:
first-order in CH3OH; zeroth-order in CH3CH2OCOCH3; first-order overall
Method of Initial Rates
The rate constant and the reaction orders must be determined experimentally by observing how the rate of a reaction changes as the concentrations of the reactants are changed. One way to do this is the method of initial rates. To use this method, select two sets of rate data where all concentrations but one are the same and set up a ratio of the two rates and the two rate laws. This will yield an equation that contains only one unknown: the reaction order of the substance whose concentration varies.
Example 4
Determining Rate Law from Initial Rates
Ozone in the upper atmosphere is depleted when it reacts with nitrogen oxides. The rates of the reactions of nitrogen oxides with ozone are important factors in deciding how significant these reactions are in the formation of the ozone hole over Antarctica.
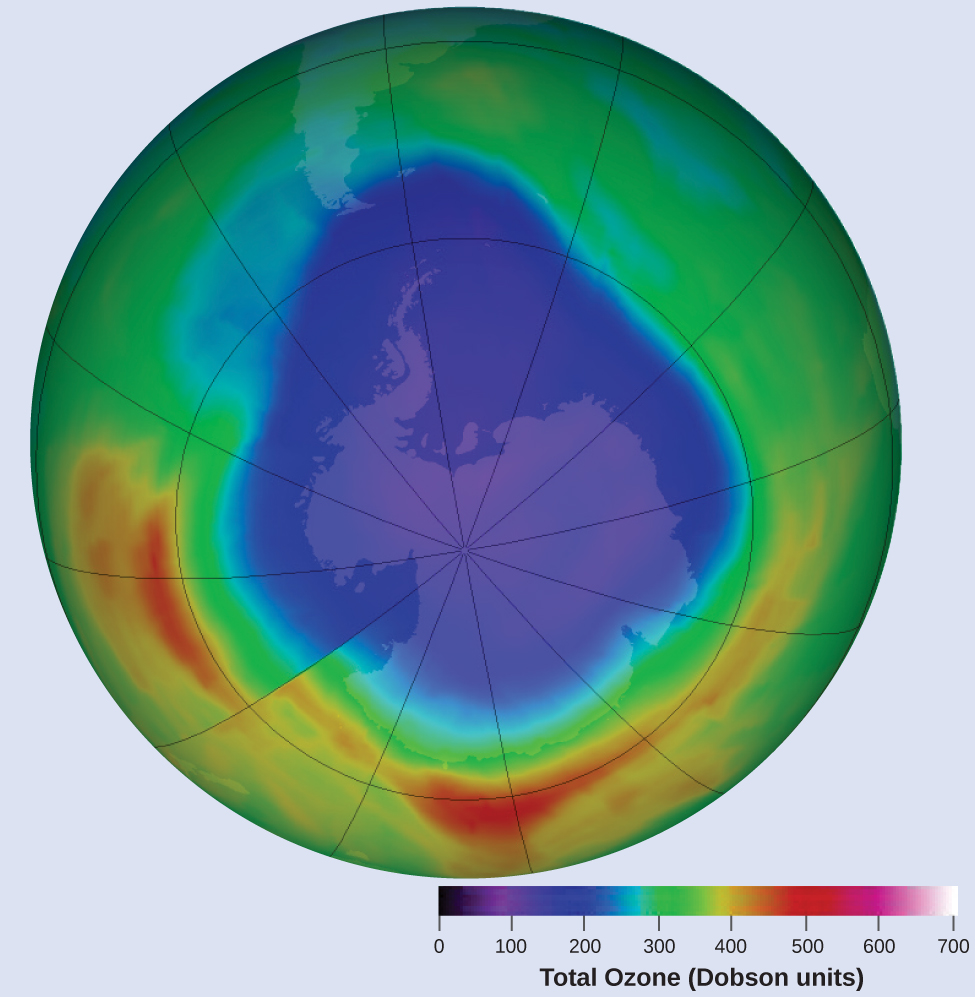
One such reaction is the combination of nitric oxide, NO, with ozone, O3:
This reaction has been studied in the laboratory, and these rate data were determined at 25 °C.
| Trial | [NO] (M) | [O3] (M) | [latex]\frac{{\Delta}[\text{NO}_2]}{{\Delta}t}\;(\text{M/s})[/latex] |
|---|---|---|---|
| 1 | 1.00 × 10−6 | 3.00 × 10−6 | 6.60 × 10−5 |
| 2 | 1.00 × 10−6 | 6.00 × 10−6 | 1.32 × 10−4 |
| 3 | 1.00 × 10−6 | 9.00 × 10−6 | 1.98 × 10−4 |
| 4 | 2.00 × 10−6 | 9.00 × 10−6 | 3.96 × 10−4 |
| 5 | 3.00 × 10−6 | 9.00 × 10−6 | 5.94 × 10−4 |
Determine the rate law and the rate constant for the reaction at 25 °C.
Solution
The rate law will have the form:
We can determine the values of m, n, and k from the experimental data using the following three-part process:
- Determine the value of m from the data in which [NO] varies and [O3] is constant (Trials 3, 4, and 5).
- When [NO] doubles from trial 3 to 4, the rate doubles, and when [NO] triples from trial 3 to 5, the rate also triples. Thus, the rate is directly proportional to [NO], and m = 1.
- Determine the value of n from data in which [O3] varies and [NO] is constant (Trials 1, 2, and 3).
- When [O3] doubles from trial 1 to 2, the rate doubles; when [O3] triples from trial 1 to 3, the rate increases also triples. Thus, the rate is directly proportional to [O3], and n = 1.
- The rate law is thus: rate = k[NO]1[O3]1
- Determine the value of k from one set of concentrations and the corresponding rate.
[latex]\begin{array}{r @{{}={}} l} k &= \dfrac{\text{rate}}{[\text{NO}][\text{O}_3]} \\[1.2em] &= \dfrac{6.60\;\times\;10^{-5}\;\rule[0.5ex]{0.7em}{0.1ex}\hspace{-0.7em}\text{M}\text{s}^{-1}}{(1.00\;\times\;10^{-6}\;\rule[0.5ex]{0.7em}{0.1ex}\hspace{-0.7em}\text{M})(3.00\;\times\;10^{-6}\;\text{M})} \\[1.0em] &= 2.20\;\times\;10^{7}\;\text{M}^{-1}\text{s}^{-1} \end{array}[/latex]
The large value of k tells us that, at 25 °C, this is a fast reaction that could play an important role in ozone depletion if [NO] is large enough.
Check Your Learning
Acetaldehyde decomposes when heated to yield methane and carbon monoxide according to the equation:
Determine the rate law and the rate constant for the reaction from the following experimental data:
| Trial | [CH3CHO] (M) | [latex]-\frac{{\Delta}[\text{CH}_3\text{CHO}]}{{\Delta}t}\;(\text{M/s})[/latex] |
|---|---|---|
| 1 | 1.75 × 10−3 | 2.06 × 10−11 |
| 2 | 3.50 × 10−3 | 8.24 × 10−11 |
| 3 | 7.00 × 10−3 | 3.30 × 10−10 |
Answer:
rate = k[CH3CHO]2, with k = 6.73 × 10−6 [latex]\frac{1}{M \cdot s}[/latex]
Example 5
Determining Rate Laws from Initial Rates
Using the initial rates method and the experimental data, determine the rate law and the value of the rate constant for this reaction:
| Trial | [NO] (M) | [Cl2] (M) | [latex]-\frac{{\Delta}[\text{NO}]}{{\Delta}t}\;(\text{M/s})[/latex] |
|---|---|---|---|
| 1 | 0.10 | 0.10 | 0.00300 |
| 2 | 0.10 | 0.15 | 0.00450 |
| 3 | 0.15 | 0.10 | 0.00675 |
Solution
The rate law for this reaction will have the form:
We can again approach this problem in a stepwise fashion, determining the values of m and n from the experimental data and then using these values to determine the value of k. In this example, however, we will use a more general approach to determine the values of m and n:
- Determine the value of m from the data in which [NO] varies and [Cl2] is constant.
- We can write the ratios with the subscripts x and y to indicate data from two different trials:
[latex]\dfrac{\text{rate}_x}{\text{rate}_y} = \dfrac{k[\text{NO}]_x^m[\text{Cl}_2]_x^n}{k[\text{NO}]_y^m[\text{Cl}_2]_y^n}[/latex]
Using trial 3 and 1 (x = 3, y = 1), in which [Cl2] does not vary, gives:
[latex]\dfrac{\text{rate}\;3}{\text{rate}\;1} = \dfrac{0.00675\;\text{M/s}}{0.00300\;\text{M/s}} = \dfrac{k(0.15\;\text{M})^m(0.10\;\text{M})^n}{k(0.10\;\text{M})^m(0.10\;\text{M})^n}[/latex]After canceling equivalent terms in the numerator and denominator, we are left with:
[latex]\dfrac{0.00675\;\text{M/s}}{0.00300\;\text{M/s}} = \dfrac{(0.15\;\text{M})^m}{(0.10\;\text{M})^m}[/latex]which simplifies to:
[latex]2.25 = (1.5)^m[/latex]We can use natural logs to determine the value of the exponent m:
[latex]\begin{array}{r @{{}={}} l} \text{ln}(2.25) &= m \times \text{ln}(1.5) \\[0.5em] \dfrac{\text{ln}(2.25)}{\text{ln}(1.5)} &= m \\[1.2em] 2 &= m \end{array}[/latex]We can confirm the result easily, since:
[latex]1.5^2 = 2.25[/latex]
- We can write the ratios with the subscripts x and y to indicate data from two different trials:
- Determine the value of n from data in which [Cl2] varies and [NO] is constant.
- The ratio between trial 2 and 1 is:
[latex]\dfrac{\text{rate}\;2}{\text{rate}\;1} = \dfrac{0.00450\;\text{M/s}}{0.00300\;\text{M/s}} = \dfrac{k(0.10\;\text{M})^m(0.15\;\text{M})^n}{k(0.10\;\text{M})^m(0.10\;\text{M})^n}[/latex]
Cancelation gives:
[latex]\dfrac{0.00450\;\text{M/s}}{0.00300\;\text{M/s}} = \dfrac{(0.15\;\text{M})^n}{(0.10\;\text{M})^n}[/latex]which simplifies to:
[latex]1.5 = (1.5)^n[/latex]Thus n must be 1, and the form of the rate law is:
[latex]\text{Rate} = k[\text{NO}]^m[\text{Cl}_2]^n = k[\text{NO}]^2[\text{Cl}_2][/latex]
- The ratio between trial 2 and 1 is:
- Determine the numerical value of the rate constant k with appropriate units.
- To determine the value of k once the rate law expression has been solved, simply plug in values from one of the experimental trial and solve for k:
[latex]\begin{array}{r @{{}={}} l} 0.00300\;\text{M/s} &= k(0.10\;\text{M})^2(0.10\;\text{M})^1 \\[0.5em] k &= 3.0\;\text{M}^{-2}\text{s}^{-1} \end{array}[/latex]
- The units for k are whatever is needed so that substituting into the rate law expression affords the appropriate units for the rate. In this example, the units for k should be [latex]\frac{1}{M^2 \cdot s}[/latex] so that the rate is in terms of M/s as given in the table.
- To determine the value of k once the rate law expression has been solved, simply plug in values from one of the experimental trial and solve for k:
Check Your Learning
Use the provided initial rate data to derive the rate law for the reaction whose equation is:
| Trial | [OCl−] (M) | [I−] (M) | Initial Rate (M/s) |
|---|---|---|---|
| 1 | 0.0040 | 0.0020 | 0.00184 |
| 2 | 0.0020 | 0.0040 | 0.00092 |
| 3 | 0.0020 | 0.0020 | 0.00046 |
Determine the rate law expression and the value of the rate constant k with appropriate units for this reaction.
Answer:
Substituting the concentration data from trial 1 and solving for k yields:
D18.5 Reaction Order and Rate Constant Units
It is often true that, as in the last "Check Your Learning" example, the reaction orders in the rate law are different from the coefficients in the chemical equation for the reaction. It is important to note that rate laws must be determined by experiment and are not reliably predicted by reaction stoichiometry.
Reaction orders play a role in determining the units for the rate constant—the units for k are whatever is needed so that substituting into the rate law expression affords the appropriate units for the rate.
The units for the rate constant for common reaction orders are summarized below.
| Overall Reaction Order (m+n) | Units of k (M1-(m+n)s-1) |
|---|---|
| zero | [latex]\dfrac{M}{s}[/latex] |
| first | [latex]\dfrac{1}{s}[/latex] |
| second | [latex]\dfrac{1}{M\;s}[/latex] |
| third | [latex]\dfrac{1}{M^2\;s}[/latex] |
Podia Question
Consider these data for the hydrolysis of benzenesulfonyl chloride (abbreviated BSC) in aqueous solution containing fluoride ions at 15 °C. The concentration of BSC was 2 × 10−4 M in all trials and from other experiments the reaction is known to be first-order in BSC. Determine the rate law for the overall reaction. Also determine numeric values for all rate constants and express them in appropriate units.
| Trial | [F−] (M) | Initial Rate (M/s) |
|---|---|---|
| 1 | 0 | 2.4 × 10−7 |
| 2 | 0.5 × 10−2 | 5.4 × 10−7 |
| 3 | 2.0 × 10−2 | 13.9 × 10−7 |
| 4 | 5.0 × 10−2 | 32.0 × 10−7 |
Suggested approach: Note that some reaction occurs with no fluoride ion present. This implies a rate law that is the sum of two rates, one for the non-fluoride reaction and one for the reaction involving fluoride ions. Determine a rate law for each of these two rates and then add the rate laws. Examples 4 and 5 should be helpful in finding the rate law for the fluoride reaction.
Two days before the next whole-class session, this Podia question will become live on Podia, where you can submit your answer.

