Unit Three
Day 22: Elementary Reactions and Reaction Mechanisms
As you work through this section, if you find that you need a bit more background material to help you understand the topics at hand, you can consult “Chemistry: The Molecular Science” (5th ed. Moore and Stanitski) Chapter 11-4 and 11-6, and/or Chapter 10.1-10.5 in the Additional Reading Materials section.
D22.1 Elementary Reactions
A balanced equation for a chemical reaction indicates what reacts, what is produced when the reaction is over, and how the amounts of reactants and products are related, but it does not necessarily show what happens on the atomic scale as the reaction takes place. Although it is not obvious on the laboratory scale, most chemical reactions occur as a series of atomic-scale steps; that is, as a sequence of simple reactions. Such a sequence of simple reactions that results in an overall reaction is called a reaction mechanism.
For example, ozone in the stratosphere protects Earth's surface from harmful ultraviolet radiation. Thus the decomposition of ozone is a very important reaction. Its overall reaction equation is
However, at the atomic scale this reaction does not involve collision and reaction of two ozone molecules. Rather, there are two steps that occur one after the other: First, one ozone molecule decomposes to an oxygen molecule and an oxygen atom. Second, the oxygen atom reacts with a second ozone molecule to give two oxygen molecules:
The two steps sum to the overall reaction. (To sum a group of chemical equations, write reactants from all equations on the left, write an arrow, and write products of all equations on the right. Then cancel anything that appears on both sides of the equation.)
Each step in a reaction mechanism is called an elementary reaction. Like chemical elements, which combine to form compounds, elementary reactions combine to make reaction mechanisms. The equation for an elementary reaction specifies exactly which atoms or molecules are involved in that reaction. For example, the second step in the mechanism above says that one gas-phase O atom reacts with one gas-phase ozone molecule and two oxygen molecules are formed. That is, for the elementary reaction to occur, one O(g) atom must collide with (come very close to) one O3(g) molecule. This is not true of the overall equation for ozone decomposition: two O3(g) molecules do not have to collide for products to appear. Because an elementary reaction describes exactly the collision required, it is possible to determine the order of an elementary reaction solely by looking at the equation. (How this works will be described later in this day's work.)
Notice that the oxygen atom that is a product in the first step of the mechanism is a reactant (and therefore reacts away) in the second step. Therefore O(g) does not appear as a product in the overall reaction. An atom, molecule, or ion that is a product in an earlier step and reacts away in a later step of a reaction mechanism is called a reaction intermediate.
D22.2 Reaction Energy Diagrams
The rates of elementary chemical reactions (and therefore of overall reactions described by reaction mechanisms) depend on the energies of the reacting atoms, molecules, or ions. Bonds often need to be broken before new bonds can be formed and energy is required to break those bonds. For example, in the ozone mechanism above, the first step involves breaking an O–O bond. Because energy is so important, it is useful to diagram the energy changes that occur as a reaction proceeds. Some indication of the progress of a reaction is chosen and then energy is plotted as a function of reaction progress.
An example of this is cis-trans isomerization—changing a cis isomer into a trans isomer. Section D8.4 explains that cis-trans isomers can be separated at room temperature because there is a barrier to rotation around an alkene double bond. The "barrier" is that the energy of the molecule increases with rotation around the double bond until an angle of 90° is reached and then decreases. Rotation requires breaking the pi part of the double bond, which is why the energy increases.
Figure 1. The pi MO in ethene is shown. Move the slider to see the two p orbitals that overlap to form the pi bond and how their overlap disappears when the front of the molecule is rotated 90°. Hover over each diagram for a description.
If the temperature increases, the average energy of the molecules also increases, so at a high enough temperature a few molecules can have more energy than is needed to break the pi part of the double bond. Molecules that have that much energy (or more) can rotate around the double bond, changing a cis isomer into a trans isomer (or the reverse). For this type of reaction, the angle of rotation around the double bond is a good measure of the progress of the reaction. Figure 2 shows energy versus reaction progress for conversion of cis-1,2-difluoroethene to trans-1,2-difluoroethene.

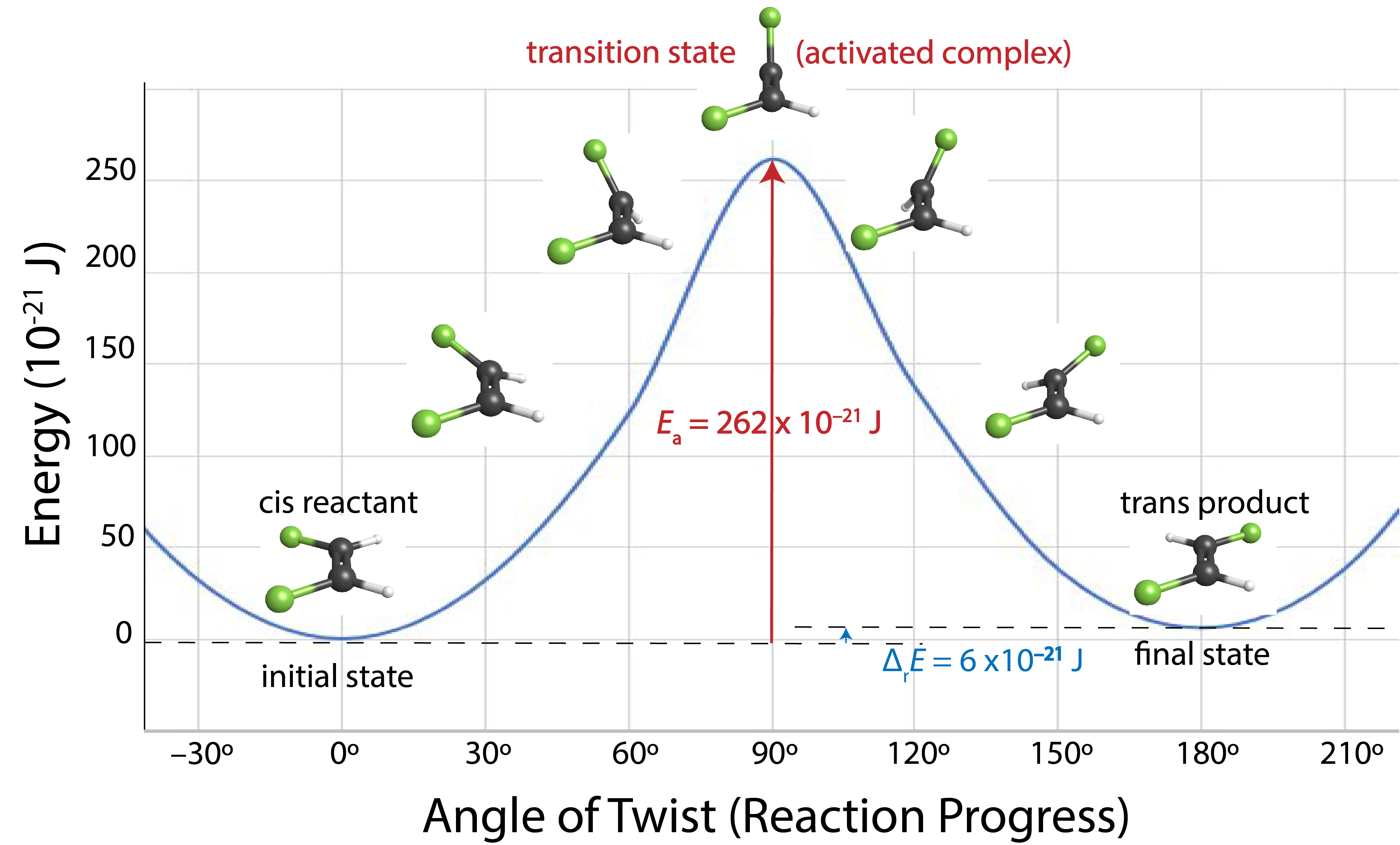
A diagram like Figure 2 that shows energy as a function of reaction progress is called a reaction energy diagram.In an elementary reaction, the reactants and products are connected by a single transition state (or activated complex), a structure that corresponds to a maximum on the reaction energy diagram. The difference in energy between the transition state and the reactants is the activation energy of the reaction, designated Ea. Notice in the diagram that the trans isomer is slightly higher in energy than the cis isomer. The difference in energy between products and reactants is the reaction energy change, ΔrE.
Eproducts – Ereactants = ΔrE,
In an overall reaction that consists of sequential elementary reaction steps, there is one transition state (and therefore one maximum in the reaction energy diagram) for each step in the mechanism connecting reactants and products (Figure 3).
D22.3 Unimolecular Elementary Reactions
A unimolecular reaction involves the rearrangement of a single reactant molecule to produce one or more products. An example unimolecular reaction is the isomerization of cis-1,2-difluoroethene shown in Figure 2. For the reaction to occur there must be rotation around the double bond. In a gas-phase sample of cis-1,2-difluoroethene, molecules are in constant motion and occasionally collide. In a collision, energy can be transferred from one molecule to another, so the energy of a given molecule can change with every collision. At any instant, some molecules are moving fast, some are moving slower, a few are hardly moving at all, and a very few are moving very fast. If a rapidly moving cis-1,2-difluoroethene molecule hits another cis-1,2-difluoroethene molecule in a way that causes a fluorine atom to start rotating around the C=C bond, and if the hit is hard enough (has enough energy), then the reaction can occur. But only a very few collisions have the 262 × 10–21 J needed to overcome the activation-energy barrier, because only a tiny fraction of the molecules has that much energy.
A general equation for a unimolecular reaction is
A → products
Suppose that a 1.0-L flask contains 0.0010 mol of reactant A. The concentration of A is 0.0010 mol/1.0 L = 0,0010 M. At any given temperature a tiny fraction of the A molecules has enough energy to overcome the activation-energy barrier and react. If we add another 0.0010 mol A to the flask, the number of A molecules doubles and the concentration of A doubles to 0.0020 M. If the temperature remains the same the fraction of molecules that has enough energy to react remains the same, but now there are twice as many molecules so the number of molecules reacting (and the rate of reaction) doubles; that is, the rate of reaction is directly proportional to the concentration of A. Thus, the rate equation for a unimolecular reaction is
If a reaction is known to be unimolecular, its reaction rate is directly proportional to concentration of reactant and the reaction is first order. Unimolecular elementary reactions are one of the building blocks from which multi-step reaction mechanisms are derived. For example, the first step in the mechanism for ozone decomposition given above, O3 → O2 + O, is a unimolecular elementary reaction that is one step of a two-step reaction mechanism.
Exercise 1: Unimolecular Reactions
D22.4 Bimolecular Elementary Reactions
The collision and reaction of two molecules or atoms in an elementary reaction is called a bimolecular reaction. There are two types of bimolecular elementary reactions. In the first type:
the two reactant molecules are different, and the rate law is first-order in A and B:
In the second type:
two identical molecules collide and react, the rate law is second-order in A:
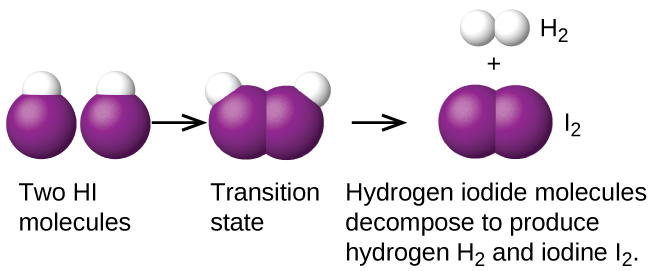
If a reaction is known to be bimolecular, then its rate law can be derived from the reaction equation. Some chemical reactions have mechanisms that consist of a single bimolecular elementary reaction. An example is the decomposition of hydrogen iodide, Figure 1:
Bimolecular reactions are building blocks for multi-step reaction mechanisms. An example is the second step in the ozone decomposition mechanism given earlier:
Molecular Collisions and Steric Factor
For a bimolecular reaction to occur, the two reactant species (atoms, molecules, or ions) must collide (come very close together), but not all collisions lead to a reaction. Thinking about collisions leads to these three ideas:
- The rate of a reaction is proportional to the rate of reactant collisions:
[latex]\text{reaction}\;\text{rate}\;{\propto}\;\dfrac{\text{number of collisions}}{\text{time}}[/latex]
- A collision that results in reaction must occur with adequate energy so that electrons can rearrange (bonds can be broken and formed).
- The reacting species must collide in an orientation that allows the reaction to proceed (this is called a steric factor).
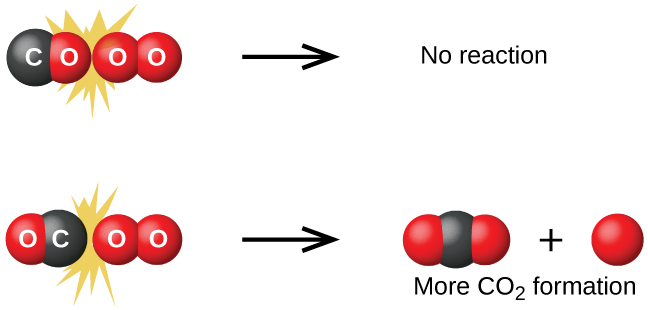
To see the importance of the third idea, consider the reaction of carbon monoxide with oxygen:
The first step in the mechanism of this reaction is bimolecular and involves a collision between two different molecules:
Consider the two collision orientations presented in Figure 5: the O2 molecule either collides with the oxygen side of CO or the carbon side. The latter is clearly more likely to result in the formation of a CO2 molecule.
The fact that collisions are required for reactions to occur also explains why most reaction rates increase as reactant concentrations increase. With an increase in the concentration of any reacting substance there are more molecules per unit volume and the chances for collisions between molecules increases. More collisions mean a faster reaction rate. At a given temperature the fraction of collisions with enough energy to surmount an activation-energy barrier is constant, so the number of reactive collisions is proportional to the number of collisions.
D22.5 Trimolecular Elementary Reactions
An elementary trimolecular reaction (or termolecular reaction) involves the simultaneous collision of three atoms or molecules. Trimolecular elementary reactions rarely occur because the probability of three particles colliding simultaneously is less than 0.1% of the probability of two particles colliding. When a reaction involves three reactant molecules, it is much more likely for it to proceed via a multi-step mechanism involving unimolecular and/or bimolecular elementary reactions.
There are, however, a few established trimolecular elementary reactions. The reaction mechanism of nitric oxide with oxygen appears to involve a trimolecular step:
Likewise, the reaction of nitric oxide with chlorine appears to involve a trimolecular step:
Exercise 2: Rate Law for an Elementary Reaction
Podia Question
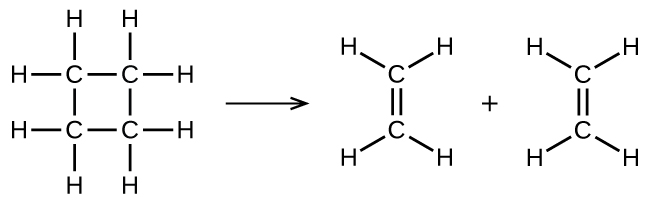
Consider the gas-phase decomposition of cyclobutane, C4H8, to ethylene, C2H4, which occurs via a unimolecular, elementary reaction:
1. Write the rate law for this reaction. Express the rate of reaction in terms of concentration. (Don't just write "rate =", use Δ[A]/Δt.)
2. Describe in words which bonds must break and which bonds must form when this reaction occurs.
3. Based on your description in part 2, suggest a structure for the activated complex (transition state) for this reaction. Use dotted lines to indicate existing bonds that are partially broken or new bonds that are partially formed.
4. At the temperature of the kinetic study the reaction energy change, ΔrE = – 300 kJ/mol. The activation energy, Ea = 261 kJ/mol. Use this information to draw a reaction energy diagram. Make the vertical axis scale as accurate as possible. Draw the structures of the reactant, the transition state, and the product molecules at appropriate positions on the diagram.
Two days before the next whole-class session, this Podia question will become live on Podia, where you can submit your answer.

