Unit Three

Day 24: Multistep Reaction Mechanisms

As you work through this section, if you find that you need a bit more background material to help you understand the topics at hand, you can consult “Chemistry: The Molecular Science” (5th ed. Moore and Stanitski) Chapter 11-7 and 11-8, and/or Chapter 10.10-10.13 in the Additional Reading Materials section.

D24.1 Rate-Determining Step in a Multi-Step Reaction

When one elementary reaction step in a multi-step reaction is significantly slower than the others, this step limits the rate at which the overall reaction occurs. For example, consider this mechanism:

A + B → C        (large Ea)

C + B → D        (small Ea)

__________________

A + 2 B → D            (overall)

The first step, with a large Ea must have a small k, so it is slow, which means that the concentration of C (which starts at zero) builds up slowly as the reaction occurs. Even though the second step has a small Ea (and therefore a large k), the second step cannot occur until the first step produces some of the intermediate, C. Because k for the second step is large, as soon as the first step produces some C, the second step reacts it away, but the second step cannot go faster than the first one because the concentration of C is always very small. Thus, the first step determines how fast the reaction can go. The slowest step in a mechanism is called the rate-determining step (or rate-limiting step).

For elementary reactions, rate laws (and reaction order) can be derived directly from the stoichiometry of the chemical equations, but this is not true for a multi-step reaction where the balanced overall equation is not an elementary reaction. For some multi-step mechanisms it is possible to derive the overall rate law from the known rate laws of the individual elementary steps. The overall rate law can also be determined from experimental data. If the experimental rate law agrees with the theoretical rate law (derived from the mechanism) the mechanism is a plausible theory for how the reaction occurs. Other experimental data can also support the plausibility of a mechanism. For example, if an intermediate proposed in the mechanism can be detected, that would support the mechanism.

D24.2 First Step is Rate-Determining

When the rate-determining step is the first step in a mechanism, the rate law for the overall reaction is the same as the rate law for the first step. The reaction of NO2 and CO provides an illustrative example:

NO2(g) + CO(g) → CO2(g) + NO(g)

At temperatures below 225 °C, the reaction is described by a rate law that is second order with respect to NO2:

rate = k[NO2]2

This is consistent with a mechanism that involves these two elementary reaction steps. Figure 1 shows a reaction energy diagram for this mechanism.

step 1) NO2(g) + NO2(g) → NO3(g) + NO(g)     (large Ea,1, slow)
step 2) NO3(g) + CO(g) → CO2(g) + NO2(g)     (small Ea,2, fast)
Figure 1. Reaction coordinate diagram for the NO2(g) + CO(g) → CO2(g) + NO(g) reaction. The sum of the two elementary reaction steps gives the net overall reaction—the NO3 that is formed in step (1) is consumed in step (2), and one of the NO2 consumed in step (1) is reformed in step (2).

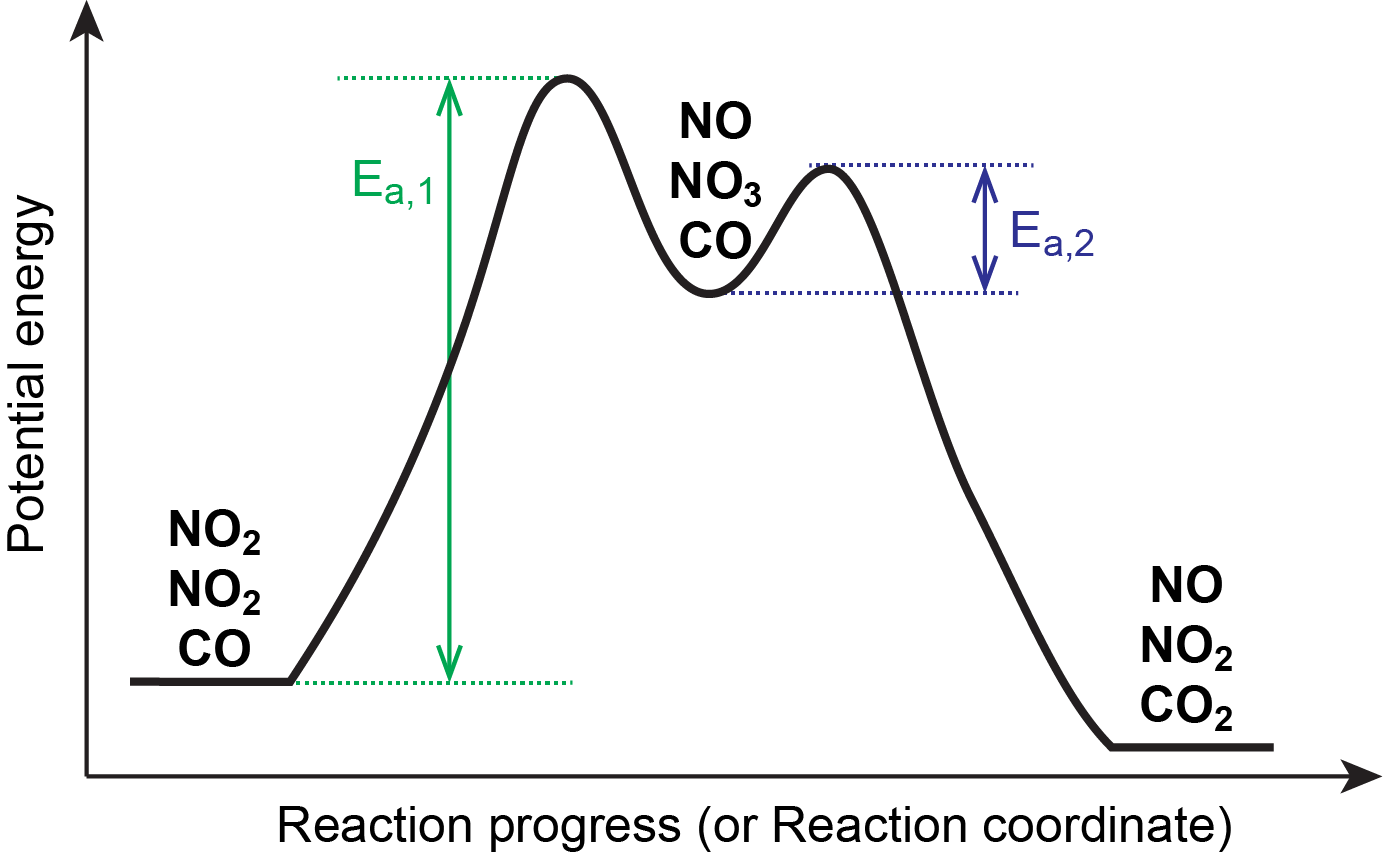
The first step is much slower than the second step and is therefore the rate-determining step. Oftentimes, the slowest reaction step is the one with the largest Ea and/or the highest energy transition state, as illustrated in Figure 1.

The stoichiometry of the rate-determining step here gives a rate law showing second-order dependence on [NO2], in agreement with the experimentally observed rate law.

D24.3 Rate-Determining Step is Not the First Step

When the rate-determining step is preceded by one or more other elementary steps, i.e. the reactants of the rate-determining step involves intermediates, the rate law for the overall reaction cannot be simply represented by the rate law of the rate-determining step. This is because concentrations of intermediates are quite difficult to determine accurately and therefore cannot be included in the overall rate law.

For example, consider the reaction of nitrogen monoxide gas with chlorine gas. The overall equation is

2 NO(g)  +  Cl2(g)  →  2 NOCl(g)

The currently accepted mechanism for this reaction is

step 1>          NO  +  Cl2  ⇄  NOCl2          fast

step 2>     NOCl2  +  NO  →  2 NOCl        slow

The first step in this mechanism is an equilibrium reaction. The second, slow step is the rate-determining step. For the rate-determining elementary reaction, whih has rate constant k2,

rate = k2 [NOCl2] [NO]

but this rate law involves the concentration of an intermediate, [NOCl2], which cannot be measured easily or controlled by experimental conditions, so it is impossible to compare this rate law to experimental data. If [NOCl2] could be expressed in terms of concentrations of reactants, then we could compare experimental and theoretical rate laws. Here is one way to do that.

The first step in the mechanism is much faster than the second step. Thus, when NOCl2 molecules are formed it is much more likely that they will decompose back to NO and Cl2 than that they will react in step 2. When enough NOCl2 has formed the rate of the unimolecular decomposition (the reverse of the first step) becomes equal to the rate at which NOCl2 forms and there is an equilibrium. An elementary reaction is at equilibrium when it proceeds in both the forward and reverse directions at equal rates. This is the reason for the two arrows pointing in opposite directions in step 1. At equilibrium,

rateforward = ratereverse

If k1 is the rate constant of the forward reaction and k-1 is the rate constant of the reverse reaction, then:

rateforward  =  k1 [NO] [Cl2]  =  k–1 [NOCl2]  = ratereverse

This expression can be solved for the concentration of NOCl2:

[latex][\text{NOCl}_2] = \left(\dfrac{k_1}{k_{-1}}\right)[\text{NO}]\;[\text{Cl}2][/latex]

The concentration of NOCl2 can now be substituted into the rate law for step 2, the rate-limiting step,

rate=kNOCl2NO=k2k1k−1NOCl2NO=k1k2k−1NO2Cl2

A product of two constants is a constant and a quotient of two constants is a constant, so k1k2/k−1 is a constant. Define that constant as k’. Then the rate law becomes,

rate  = k’ [NO]2 [Cl2]

If the mechanism given at the beginning of this section is correct, the reaction is first-order in Cl2 and second-order in NO.

D24.4 Catalysis

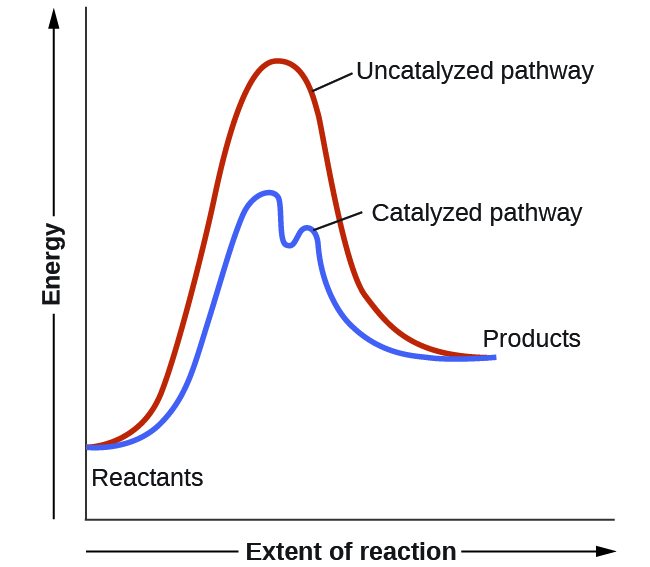
A catalyst increases the rate of a reaction by altering the mechanism, allowing the reaction to proceed via a pathway with lower activation energy than for the uncatalyzed reaction. In a typical catalyzed reaction, the catalyst interacts with a reactant to form an intermediate substance, which then decomposes or reacts with another reactant in one or more steps to regenerate the original catalyst and form product. Hence, the catalyst is involved in the reaction mechanism but is not consumed by the reaction.

A catalyzed mechanism must involve at least two steps, one where the catalyst reacts with a reactant to form an intermediate and one where an intermediate regenerates the catalyst. Usually there are more mechanistic steps in a catalyzed reaction than in the uncatalyzed mechanism, as shown in Figure 2. The lower Ea in the catalyzed pathway results in an increase in rate as described by the Arrhenius equation. Note that a catalyst decreases the activation energy for both the forward and the reverse reactions and hence accelerates both the forward and the reverse reactions. Consequently, the presence of a catalyst will permit a system to reach equilibrium more quickly, but it has no effect on the relative energies of the reactants and products.

A graph is shown with the label, “Extent of reaction,” appearing in a right pointing arrow below the x-axis and the label, “Energy,” in an upward pointing arrow just left of the y-axis. Approximately one-fifth of the way up the y-axis, a very short, somewhat flattened portion of both a red and a blue curve are shown. This region is labeled “Reactants.” A red concave down curve extends upward to reach a maximum near the height of the y-axis. This curve is labeled, “Uncatalyzed pathway.” From the peak, the curve continues downward to a second horizontally flattened region at a height of about one-third the height of the y-axis. This flattened region is labeled, “Products.” A second curve is drawn in blue with the same flattened regions at the start and end of the curve. The height of this curve is about two-thirds the height of the first curve and just right of its maximum, the curve dips low, then rises back and continues a downward trend at a lower height, but similar to that of the red curve. This blue curve is labeled, “Catalyzed pathway.”
Figure 2. This reaction energy diagram shows the effect of a catalyst. The catalyst provides an alternate reaction pathway with a lower activation energy. In this case, the catalyzed pathway involves a two-step mechanism (note the presence of two transition states) and an intermediate species (represented by the valley between the two transitions states). Other catalyzed reactions might have more than two steps.

Example 2

Using Reaction Diagrams to Compare Catalyzed and Uncatalyzed Reactions
The two reaction diagrams here represent the same reaction: one without a catalyst and one with a catalyst. Identify which diagram suggests the presence of a catalyst, explain why you chose that diagram, and determine the activation energy for the catalyzed reaction: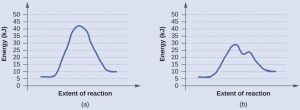In this figure, two graphs are shown. The x-axes are labeled, “Extent of reaction,” and the y-axes are labeled, “Energy ( k J ).” The y-axes are marked off from 0 to 50 in intervals of five. In a, a blue curve is shown. It begins with a horizontal segment at about 6. The curve then rises sharply near the middle to reach a maximum of about 42 and similarly falls to another horizontal segment at about 10. In b, the curve begins and ends at the same values, but there are two maxima near the center of the graph; the higher of these is at about 29 and the lower at about 25. Between the maxima the curve dips to about 22.

Solution

A catalyst does not affect the energy of reactants or products, so those aspects of both diagrams are the same. There are two major differences between the graphs: graph (b) has two maxima and the highest maximum is significantly lower than for (a). This indicates the use of a catalyst in (b). The activation energy is the difference between the energy of the starting reagents and the transition state—a maximum on the reaction coordinate diagram. In (b) the reactants are at 6 kJ/mol and the transition state is at 29 kJ/mol, so the activation energy can be calculated as follows:

Ea = 29 kJ/mol – 6 kJ/mol = 23 kJ/mol

Check Your Learning
Determine which of the two diagrams here (both for the same reaction) involves a catalyst, and identify the activation energy for the catalyzed reaction:
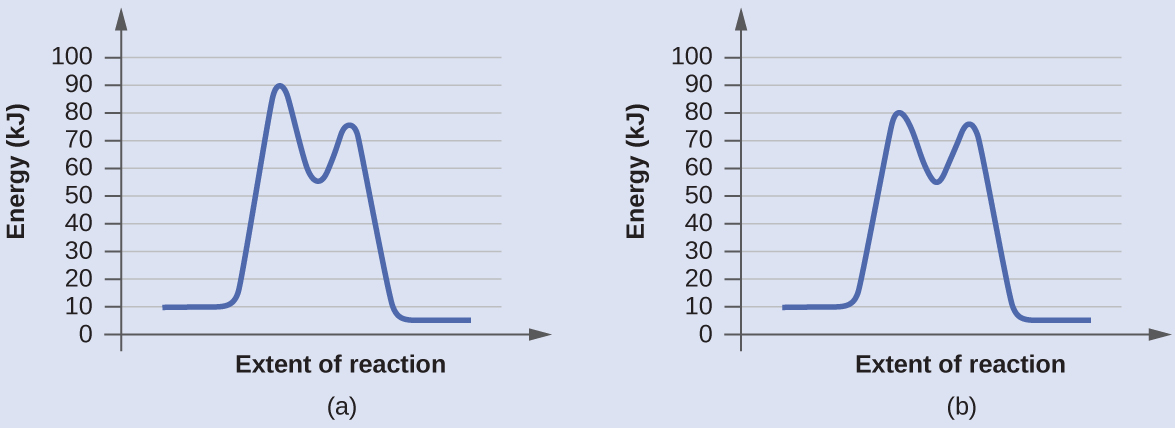
In this figure, two graphs are shown. The x-axes are labeled, “Extent of reaction,” and the y-axes are labeledc “Energy (k J).” The y-axes are marked off from 0 to 100 at intervals of 10. In a, a blue curve is shown. It begins with a horizontal segment at about 10. The curve then rises sharply near the middle to reach a maximum of about 91, then sharply falls to about 52, again rises sharply to about 73 and falls to another horizontal segment at about 5. In b, the curve begins and ends similarly, but the first peak reaches about 81, drops to about 55, then rises to about 77 before falling to the horizontal region at about 5.

Answer:

Diagram (b) is a catalyzed reaction with an activation energy of about 70 kJ/mol. Both the uncatalyzed and the catalyzed reactions have two steps in the mechanism but the steps are different.

Exercise 1: Catalytic Mechanisms

Consider this reaction mechanism:

(Step 1)     A + A → C

(Step 2)      C + B → D

(Step 3)      D → E + B

I. Classify all species according to whether they are reactants, intermediates, catalysts, or products in the overall reaction.

Podia Question

Here is the general reaction mechanism shown in Exercise 1:

(Step 1)         A + A → C

(Step 2)        C + B → D

(Step 3)        D → E + B

Make these assumptions:

  • Step 3 is the rate-determining step in the mechanism;
  • Steps 1 and 2 are equilibrium reactions;
  • The reaction is exothermic by 14 kJ/mol; that is, the energy of the products is 14 kJ/mol less than the energy of the reactants;
  • The activation energy is 73 kJ/mol.

1. Draw a reaction energy diagram for this reaction. If you need to make any additional assumptions to draw the diagram, describe each additional assumption.

2. Derive the rate law for this reaction; express the rate of reaction in terms of concentrations of reactants and catalyst.

Two days before the next whole-class session, this Podia question will become live on Podia, where you can submit your answer.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chemistry 109 Copyright © by John Moore; Jia Zhou; and Etienne Garand is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.