Unit Three
Day 26: Thermochemistry
As you work through this section, if you find that you need a bit more background material to help you understand the topics at hand, you can consult “Chemistry: The Molecular Science” (5th ed. Moore and Stanitski) Chapter 4, and/or Chapter 11.1-11.4 in the Additional Reading Materials section.
D26.1 Energy, Temperature, and Heat
Energy can be defined as the capacity to do work, that is, to move an object against a force. For example, energy provided to your body by chemical reactions enables you to climb a ladder against the force of gravity. Kinetic energy is energy that an object has because it is moving. Each molecule in a sample of argon gas is moving and therefore has kinetic energy. The gas molecules could do work by pushing against an object and moving it, so the kinetic energy of gas molecules could be converted to kinetic energy of a moving piston, for example. Potential energy is energy that an object has because of its position. When you reach the top of a ladder your potential energy is greater than it was at the bottom because Earth's gravity attracts you downward. Should you fall off the ladder, gravitational attraction would accelerate you toward the ground, converting some of the potential energy into kinetic energy.
The Law of Conservation of Energy states that although energy can be changed from one form to another, the total quantity of energy in the universe is constant. Thus, if potential energy is converted to kinetic energy the quantity of kinetic energy at the end must equal the quantity of potential energy at the beginning. When all forms of energy are considered, whenever anything occurs the change in energy must be zero; that is, for any process, ΔEoverall = 0.
Thermal energy is kinetic energy associated with the random motion of atoms and molecules. When energy is transferred to a sample of matter, the atoms and molecules move more quickly, they have a higher average kinetic energy (KE), the object's temperature increases, and we say that the object is “hotter.” When thermal energy is transferred out of an object, the atoms and molecules move more slowly, they have lower average KE, the object's temperature decreases, and we say that the object is “colder”.
Click on this interactive simulation to view the effects of temperature on molecular motion. Choose "States", then choose "argon" and "solid", and then explore the effect of temperature. See whether you can determine the melting and boiling points.
Heating (or heat), represented by q, is the transfer of thermal energy between two bodies at different temperatures (Figure 1).
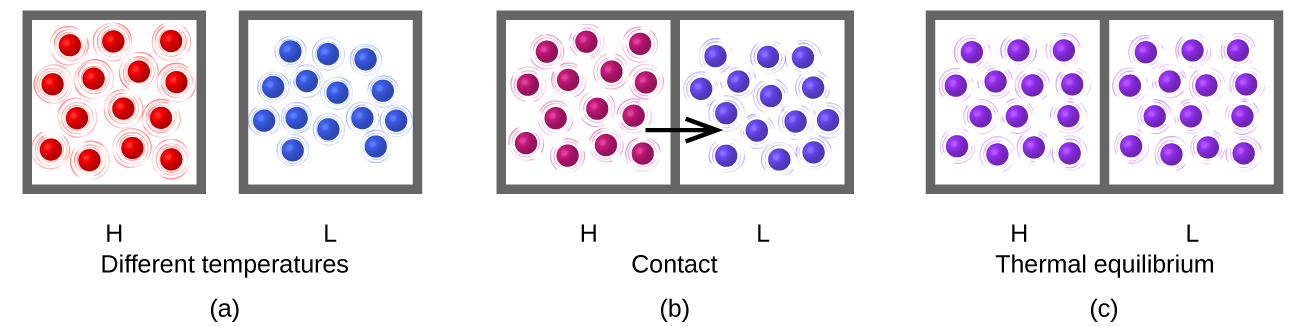
Working (or work), represented by w, is a process that transfers kinetic energy to or from a macroscopic object. When a golf club strikes a golf ball, for example, the club does work on the ball, accelerating the ball to a high speed. Because heat and work involve transfers of energy, we will speak of heat as "a heat transfer of energy" and work as "a work transfer of energy". Most chemists just use "heat" and "work" to mean the same thing.
The SI unit of heat, work, and energy is the joule (1 J = 1 kg m2/s2). One joule is the energy transferred to an object when a force of 1 newton acts on the object through a distance of 1 meter. It is named in honor of the English physicist James Prescott Joule.
The heat capacity (C) of a sample of matter is the heat transfer of energy required when the object's temperature changes by one kelvin (ΔT = 1 K). (Because 1 K is the same size as 1 °C, ΔT has the same numeric value whether expressed in K or °C.)
Heat capacity depends on both the type and the quantity of substance, and therefore is an extensive property—its value is proportional to the quantity of the substance.
The specific heat capacity (c) of a substance is the heat transfer of energy required to raise the temperature of 1 g of a substance by 1 °C (or 1 kelvin):
Specific heat capacity depends only on the kind of substance and is an intensive property—the type, but not the quantity, of the substance is all that matters. It is typically reported in units of J/g °C. The molar heat capacity, also an intensive property, is the heat capacity per mole of a particular substance and typically has units of J/mol °C.
The specific heat capacity of a substance varies somewhat with temperature. However, this variation is usually small enough that we will treat specific heat capacity as constant over the range of temperatures that will be considered in this course. Specific heat capacities of some common substances are listed in Table 1.
| Substance | Symbol (state) | Specific Heat Capacity (J/g °C) |
|---|---|---|
| helium | He(g) | 5.193 |
| water | H2O(l) | 4.184 |
| ethanol | C2H6O(l) | 2.376 |
| ice | H2O(s) | 2.093 (at −10 °C) |
| water vapor | H2O(g) | 1.864 |
| nitrogen | N2(g) | 1.040 |
| oxygen | O2(g) | 0.918 |
| aluminum | Al(s) | 0.897 |
| carbon dioxide | CO2(g) | 0.853 |
| argon | Ar(g) | 0.522 |
| iron | Fe(s) | 0.449 |
| copper | Cu(s) | 0.385 |
| lead | Pb(s) | 0.130 |
| gold | Au(s) | 0.129 |
| silicon | Si(s) | 0.712 |
| Table 1. Specific Heat Capacities of Common Substances at 25 °C and 1 bar | ||
If we know the mass of a substance and its specific heat capacity, we can calculate the heat transfer of energy, q, to or from the substance by measuring the temperature change during heating or cooling:
If a substance gains thermal energy, its temperature increases, its ΔT is positive, and the value of q is positive. If a substance loses thermal energy, its temperature decreases, its ΔT is negative, and the value of q is negative.
Example 1
Measuring Heat Transfer of Energy
A flask containing 8.0 × 102 g of water is heated, and the temperature of the water increases from 21 °C to 85 °C. How much heat did the water absorb (how much heat transfer of energy to the water took place)?
Solution
To answer this question, consider these factors:
- the specific heat capacity of the substance being heated (in this case, water)
- the mass of substance being heated (in this case, 800 g)
- the temperature change (in this case, from 21 °C to 85 °C).
The specific heat capacity of water is 4.184 J/g °C. Since 4.184 J is required to heat 1 g of water by 1 °C, we will need 800 times as much to heat 800 g of water by 1 °C. And, we will need 64 times as much to heat it by 64 °C (that is, from 21 °C to 85 °C).
This can be summarized using the equation:
Because the temperature increased, there was a heat transfer of energy to the water and q is positive.
Check Your Learning
How much heat transfer of energy, in joules, is required to increase the temperature of a 5.00 × 102-g iron skillet from 25 °C to 250 °C? The specific heat capacity of iron is 0.451 J/g °C.
Answer:
5.07 × 104 J
Exercise 1: Specific Heat Capacity and Temperature Change
Calculate the energy transfer needed to heat 1.00 kg of the following samples by 2.00 °C. (Enter your answers using 3 significant figures. Do not use scientific notation.)
Exercise 2: Heating a Hot Tub
You are thinking about using a 1500-W (1500-watt) water heater to heat a hot tub holding 1700 L of 20. °C water. Calculate how many hours would it take to heat the water to a comfy 38 °C? (Assume no transfer of energy from the water to the rest of the hot tub or surroundings.) The specific heat capacity of water is 4.184 J/g °C. The density of water is 0.995 g/mL. 1 Watt = 1 J/s. (Enter your answers using 2 significant figures.)
D26.2 Calorimetry
Calorimetry is an experimental technique used to measure quantitatively heat transfers of energy. Energy is exchanged with a calorimeter, a device whose heat capacity is known and therefore can relate temperature change to quantity of energy transferred. The calorimeter is insulated thermally so that energy does not transfer beyond its physical boundaries. In calorimetry it is useful to define a system, the substance(s) undergoing the chemical or physical change, and the surroundings, everything else that can exchange energy with the system.
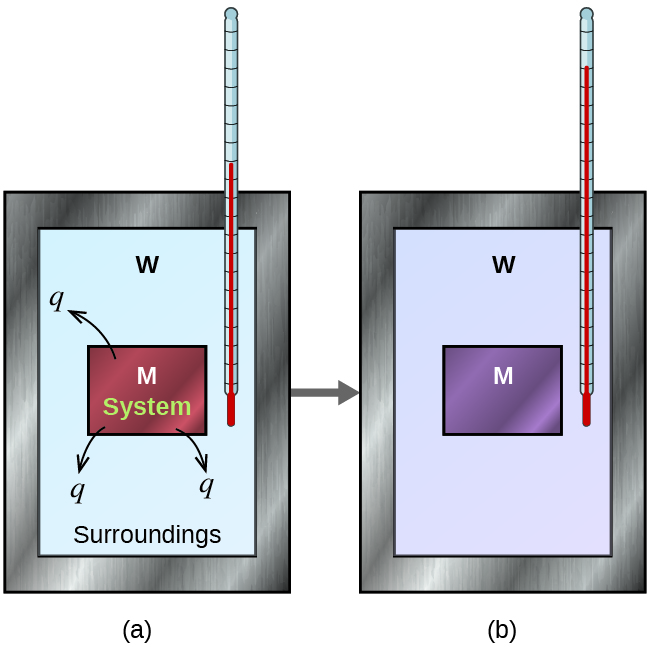
Consider a simple example that illustrates the core idea behind calorimetry. Suppose we initially have a hot piece of metal (M) and cool water (W). If we place the metal in the water, there will be heat transfer of energy from M to W, until the two substances have the same temperature; that is, until they reach thermal equilibrium (Figure 3). If this occurs in a well insulated calorimeter, ideally all of this heat transfer of energy occurs between the two substances, with no heat transfer of energy either to or from the calorimeter or anything else. Under these ideal circumstances,
The magnitude of q is therefore the same for both substances. The arithmetic sign of either q value is determined by whether the matter in question loses or gains energy. In the situation described, the heat transfer of energy is from the metal (which has less energy at the end, qM negative) to the water (which has more energy at the end, qW positive).
Example 2
Heat Transfer between Substances at Different Temperatures
A 360-g piece of rebar (a steel rod used for reinforcing concrete) is dropped into 425 g of water at 24.0 °C. The final temperature of the water was measured as 42.7 °C. Calculate the initial temperature of the piece of rebar. Assume the specific heat of steel is approximately 0.449 J/g ºC, and that all heat transfer occurs between the rebar and the water.
Solution
The temperature of the water increases from 24.0 °C to 42.7 °C, so the water absorbs heat. That heat came from the piece of rebar, which initially was at a higher temperature. Assuming that all heat transfer was between the rebar and the water, then heat given off by rebar = −heat taken in by water, or:
Letting f = final and i = initial, in expanded form, this becomes:
Noting that the final temperature of both the rebar and water is 42.7 °C, substituting known values yields:
[latex]T_{\text{i, rebar}} = \dfrac{(4.184 \;\text{J/g} \;^\circ\text{C})(425 \;\text{g})(42.7 \;^\circ\text{C} - 24.0 \;^\circ\text{C})}{(0.449 \;\text{J/g} \;^\circ\text{C})(360 \;\text{g})} + 42.7 \;^\circ\text{C}[/latex]
Solving this gives Ti,rebar= 248 °C.
Check Your Learning
A 248-g piece of copper is dropped into 390 g of water at 22.6 °C. The final temperature of the water was measured as 39.9 °C. Calculate the initial temperature of the piece of copper. Assume that all heat transfer occurs between the copper and the water.
Answer:
The initial temperature of the copper was 335.6 °C.
Check Your Learning
A 248-g piece of copper initially at 314 °C is dropped into 390 g of water initially at 22.6 °C. Assuming that all heat transfer occurs between the copper and the water, calculate the final temperature.
Answer:
The final temperature (reached by both copper and water) is 38.7 °C.
Example 3
Identifying a Metal by Measuring Specific Heat Capacity
A 59.7 g piece of metal that had been submerged in boiling water was quickly transferred into 60.0 g of water initially at 22.0 °C. The final temperature is 28.5 °C. Use these data to determine the specific heat capacity of the metal. Use this result to identify the metal.
Solution
Assuming perfect heat transfer:
Noting that since the metal was submerged in boiling water, its initial temperature was 100.0 °C, we have:
Solving this:
Comparing this with values in Table 1, our experimental specific heat capacity is closest to the value for copper (0.385 J/g °C), so we identify the metal as copper.
Check Your Learning
A 92.9-g piece of a silver/gray metal is heated to 178.0 °C, and then quickly transferred into 75.0 g of water initially at 24.0 °C. After 5 minutes, both the metal and the water have reached the same temperature: 29.7 °C. Determine the specific heat capacity and the identity of the metal. (Note: You should find that the specific heat capacity is close to that of two different metals. Explain how you can confidently determine the identity of the metal).
Answer:
cmetal= 0.13 J/g °C
This specific heat is close to that of either gold or lead. It would be difficult to determine which metal this was based solely on the numerical values. However, the observation that the metal is silver/gray in addition to the value for the specific heat indicates that the metal is lead.
Calorimetry can be applied to chemical reactions. When a chemical reaction takes place there is usually a sizable transfer of energy. That is, there is usually a significant change in temperature as reactants become products. A reaction in which there is heat transfer of energy from the reacting substances to their surroundings (a reaction that heats the surroundings) is called an exothermic reaction. For example, the combustion reaction that occurs in the flame of a lighted match is exothermic. A reaction in which there is heat transfer of energy from the surroundings to the system (a reaction that cools the surroundings) is an endothermic reaction. For example, when the substances in a cold pack (water and a salt such as ammonium nitrate) are mixed, the resulting process transfers energy from the surroundings, making the surroundings colder.
The same principles apply when we use calorimetry to determine the heat transfer of energy involved in a chemical reaction: the heat transfer of energy of the system (defined as all atoms present in reactants and products), qreaction, plus the heat transfer of the surroundings, qsurroundings, add up to zero:
Example 4
Heat Transfer of Energy by an Exothermic Reaction
When 50.0 mL of 0.10 M HCl(aq) and 50.0 mL of 0.10 M NaOH(aq), both at 22.0 °C, are added to a coffee cup calorimeter, the temperature of the mixture reaches a maximum of 28.9 °C. Calculate the heat transfer of energy when this reaction occurs . A coffee-cup calorimeter consists of two nested styrofoam cups, a cork lid, a stirrer, and a temperature probe. Make these assumptions: the styrofoam cups, cork, stirrer, and temperature probe have negligible heat capacity and therefore are not involved in energy transfer; there is no energy transfer from inside to outside the calorimeter; the volume of the mixed solutions is the sum of the original volumes; and the solution has the same specific heat capacity and density as water.
Solution
To visualize what happens, imagine that you could combine the two solutions so quickly that no reaction took place; then after mixing, the reaction took place. At the instant of mixing, you have 100.0 mL of a mixture of HCl and NaOH at 22.0 °C. The HCl and NaOH then react until the solution temperature reaches 28.9 °C.
Because the calorimeter has negligible heat capacity and is well insulated (no energy transfer from inside to outside), the heat transfer of energy for the reaction is equal to the heat transfer of energy for the solution. Therefore:
Next, we know that the heat absorbed by the solution depends on its specific heat, mass, and temperature change:
We assumed that the solution has the same density and specific heat capacity as water. The density of water is approximately 1.0 g/mL, so 100.0 mL has a mass of about 1.0 × 102 g. (Because there are only two significant figures in the solution concentrations, two significant figures should be adequate.). The specific heat capacity of water is approximately 4.18 J/g °C, so we use that for the specific heat capacity of the solution. Substituting these values gives:
Finally, since we are trying to find the heat transfer of energy for the reaction, we have:
The negative sign indicates that the reaction is exothermic. It produces 2.89 kJ of heat.
Check Your Learning
When 100 mL of 0.200 M NaCl(aq) and 100 mL of 0.200 M AgNO3(aq), both at 21.9 °C, are mixed in a coffee cup calorimeter, the temperature increases to 23.5 °C as solid AgCl forms. Calculate the heat transfer of energy for this precipitation reaction. List the assumptions you made to determine your value.
Answer:
1.34 × 103 J; assume no heat is absorbed by the calorimeter, no heat is exchanged between the calorimeter and its surroundings, and that the specific heat capacity and density of the solution are the same as those for water
This link shows the precipitation reaction that occurs when the disk in a chemical hand warmer is flexed.
Example 5
Heat Transfer of Energy in an Instant Ice Pack
When solid ammonium nitrate dissolves in water, the solution becomes cold. This is the basis for an “instant ice pack”. When 3.21 g of solid NH4NO3 dissolves in 50.0 g of water at 24.9 °C in a calorimeter, the temperature decreases to 20.3 °C.
Calculate q for this process and explain the meaning of its arithmetic sign. State any assumptions that you made.

Solution
We assume that the calorimeter prevents heat transfer between the solution and its external environment (including the calorimeter itself), in which case:
Assuming also that the specific heat of the solution is the same as that for water, we have:
The positive sign for q indicates that the dissolution is an endothermic process.
Check Your Learning
When a 3.00-g sample of KCl was added to 3.00 × 102 g of water in a coffee cup calorimeter, the temperature decreased by 1.05 °C. Calculate the heat transfer of energy for dissolving the KCl. List assumptions you made.
Answer:
1.33 kJ; assume that the calorimeter prevents heat transfer between the solution and its external environment (including the calorimeter itself) and that the specific heat capacity of the solution is the same as that for water
If the heat capacity of a calorimeter is too large to neglect or if we require more accurate results, then we must take into account the heat transfer of energy for the calorimeter as well as for the solution.
Coffee-cup calorimeters are designed to operate at constant (atmospheric) pressure and are convenient to measure heat transfers of energy accompanying processes that occur in solution. A different type of calorimeter that operates at constant volume, colloquially known as a bomb calorimeter, is used to measure energy transfers for reactions such as combustion reactions.

Example 6
Bomb Calorimetry
When 3.12 g of glucose, C6H12O6, was burned in a bomb calorimeter in an excess of oxygen, the temperature of the calorimeter increased from 23.8 °C to 35.6 °C. The calorimeter contained 775 g of water, and the bomb had a heat capacity of 893 J/°C. Calculate the heat transfer of energy associated with combustion of the glucose sample. Assume all heat transfer of energy is between the reaction system and the bomb and water.
Solution
Nearly all the combustion-reaction energy is transferred to the water and the bomb. The heat evolved by the reaction is absorbed by the water and the bomb:
This reaction released 48.7 kJ of heat when 3.12 g of glucose was burned.
Check Your Learning
When 0.963 g of benzene, C6H6, is burned in a bomb calorimeter, the temperature of the calorimeter increases by 8.39 °C. The bomb has a heat capacity of 784 J/°C and is submerged in 925 g of water. How much heat was produced by the combustion of the glucose sample?
Answer:
39.0 kJ
Click on this link to access the US Department of Agriculture (USDA) National Nutrient Database, containing nutritional information on over 8000 foods.
D26.3 Enthalpy
Chemical thermodynamics deals with the relationships between heat, work, and other means of energy transfer in the context of chemical and physical processes.
Substances act as reservoirs of energy. The total of all possible kinds of energy present in a substance is called the internal energy (U), sometimes symbolized as E. Energy is transferred into a system when it is heated (q) by the surroundings or when the surroundings does work (w) on the system. For example, energy can be transferred into room-temperature metal wire if it is immersed in hot water (the water heats the wire), or if you rapidly bend the wire back and forth (the wire becomes warmer because of the work done on it). Both processes increase the internal energy of the wire, which is reflected in an increase in the wire’s temperature.
The relationship between internal energy, heat, and work can be represented by the equation,
assuming there are no energy transfers other than heat and work.
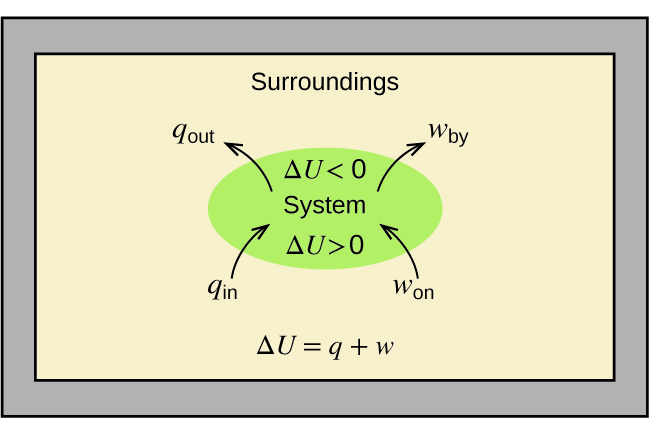
This is one version of the first law of thermodynamics, the law of conservation of energy. The equation shows that the internal energy of a system changes through heat transfer of energy into or out of the system (positive q is heat transfer in; negative q is heat transfer out) or work done on or by the system. The work, w, is positive if it is done on the system (increases internal energy) and negative if it is done by the system. Figure 4 summarizes these relationships.
This view of an internal combustion engine illustrates the conversion of energy produced by the exothermic combustion reaction of a fuel such as gasoline into energy of motion.
Internal energy is a type of quantity known as a state function (or state variable), whereas heat and work are not state functions. The value of a state function depends only on the state that a system is in, and not on how that state is reached. If a quantity is not a state function, then its value does depend on how the state is reached. An example of a state function is altitude or elevation. If you stand on the summit of Mt. Kilimanjaro, you are at an altitude of 5895 m, and it does not matter whether you hiked there or parachuted there. The distance you traveled to the top of Kilimanjaro, however, is not a state function. You could climb to the summit by a direct route or by a more roundabout, circuitous path. Other familiar state functions are temperature, volume, and pressure.
Chemists ordinarily use a property known as enthalpy (H) to describe the thermodynamics of chemical and physical processes:
Because it is derived from three state functions (internal energy (U), pressure (P) and volume (V)), enthalpy is also a state function.
Enthalpy values for specific substances cannot be measured directly; only enthalpy changes for chemical or physical processes can be determined. For processes that take place at constant pressure (a common condition for many chemical and physical changes that take place at atmospheric pressure), the enthalpy change (ΔH) is:
(where P is factored out of Δ(PV) because P is constant). The mathematical product PΔV represents work (w), called expansion or pressure-volume work. By their definitions, the arithmetic signs of ΔV and w are always opposite:
Substituting yields:
where qp is the heat of reaction under constant pressure. Therefore, if a chemical or physical process is carried out at constant pressure with the only work done caused by expansion or contraction, then the heat flow (qp) equals enthalpy change (ΔH) for the process.
The heat given off when you operate a Bunsen burner is equal to the enthalpy change of the methane combustion reaction that takes place, because it occurs at the essentially constant pressure of the atmosphere. On the other hand, the heat produced by a reaction measured in a bomb calorimeter is not equal to ΔH because the closed, constant-volume metal container prevents expansion work from occurring. Chemists usually perform experiments under normal atmospheric conditions, at constant external pressure with qp = ΔH, which makes enthalpy the most convenient choice for determining heat transfer of energy.
Heat effects of chemical reaction are summarized in thermochemical expressions. A thermochemical expression is a balanced chemical equation together with a value of ΔrH°, the standard-state reaction enthalpy, and a temperature. The standard-state reaction enthalpy change, ΔrH°, is the standard-state enthalpy of pure, unmixed reaction products minus the standard-state enthalpy of pure, unmixed reactants; that is, the enthalpy change for the reaction under standard-state conditions. Standard-state conditions means a pressure of 1 bar and a specified temperature. Sometimes the temperature is not specified, which usually means a temperature of 298.15 K (25.0 °C) is assumed. For example, consider this thermochemical expression:
2 H2(g) + O2(g) → 2 H2O(g) ΔrH° = −483.6 kJ/mol (25 °C)
This refers to reaction of two molecules of hydrogen with 1 molecule of oxygen to form two molecules of water, all in the gas phase. If this reaction equation took place once, the two hydrogen molecules and the one oxygen molecule would react to form two water molecules and 8.031 × 10−19 J would be transferred to the surroundings. Because we are interested in laboratory-scale reactions, where moles of reactants are involved, ΔrH° is reported per mole of reaction. A mole of reaction involves a chemical reaction equation happening 6.022 × 1023 times; in this case that is 2 mol H2(g) reacting with 1 mol O2(g) to give 2 mol H2O(g). The heat transfer of energy to the surroundings is then 8.031 × 10−19 J × 6.022 × 1023 mol−1 = 483.6 kJ/mol. Because the energy transfer is from system to surroundings, the sign is negative and ΔrH° = −483.6 kJ/mol.
These conventions apply to thermochemical expressions:
- In a thermochemical expression, the listed ΔrH° value indicates the quantity of heat transfer of energy for the coefficients in the chemical equation. If the coefficients are multiplied by some factor, ΔrH° must be multiplied by that same factor. In other words, ΔrH° is an extensive property. For example:
[latex]\begin{array}{l l} \text{H}_2(g) + \frac{1}{2} \text{O}_2(g) \longrightarrow \text{H}_2 \text{O} (l) & \Delta _\text{r}H\text{°} = -286 \;\text{kJ/mol} \\[1em] (\text{two-fold increase in amounts}) \\ 2\; \text{H}_2(g) + \text{O}_2(g) \longrightarrow 2 \text{H}_2 \text{O}(l) & \Delta _\text{r}H\text{°} = 2 \times (-286 \;\text{kJ/mol}) = -572 \;\text{kJ} \\[1em] (\text{two-fold decrease in amounts}) \\ \frac{1}{2} \text{H}_2(g) + \frac{1}{4} \text{O}_2(g) \longrightarrow \frac{1}{2} \text{H}_2 \text{O}(l) & \Delta _\text{r}H\text{°} = \frac{1}{2} \times (-286 \;\text{kJ}) = -143 \;\text{kJ/mol} \end{array}[/latex]
- ΔrH° of a reaction depends on the physical state of the reactants and products (whether we have gases, liquids, solids, or aqueous solutions), so these must be shown.
- A negative ΔrH° indicates an exothermic reaction; a positive ΔrH° indicates an endothermic reaction. If the direction of a chemical equation is reversed, the arithmetic sign of its ΔrH° is changed (a process that is endothermic in one direction is exothermic in the opposite direction).
Example 7
Measurement of a Standard Reaction Enthalpy Change
When 0.0500 mol of HCl(aq) reacts with 0.0500 mol of NaOH(aq) to form 0.0500 mol of NaCl(aq), 2.9 kJ is transferred to the surroundings. Calculate ΔrH° , the enthalpy change per mole of reaction.
Solution
For the reaction of 0.0500 mol acid (HCl), q = −2.9 kJ. This means:
Because the coefficient of HCl in the chemical equation is 1, there is 1 mol HCl per mol reaction and we write the thermochemical equation as
Check Your Learning
When 1.34 g Zn(s) reacts with 60.0 mL of 0.750 M HCl(aq), the reaction is exothermic by 3.14 kJ. Determine ΔrH°.
Answer:
ΔrH° = −153 kJ/mol
Be sure to take both stoichiometry and limiting reactants into account when determining the ΔrH° for a chemical reaction.
Example 8
Determining Standard Reaction Enthalpy Change
A gummy bear contains 2.67 g sucrose, C12H22O11. When it reacts with 7.19 g potassium chlorate, KClO3, 43.7 kJ is evolved. Determine ΔrH° for the reaction
Solution
We have:
[latex]7.19 \;\rule[0.5ex]{0.6em}{0.1ex}\hspace{-0.6em}\text{g} \times \dfrac{1 \;\text{mol}}{122.5 \;\rule[0.25ex]{0.55em}{0.1ex}\hspace{-0.55em}\text{g}} = 0.0587 \;\text{mol KClO}_3[/latex]
Since
C12H22O11 is the excess reactant and KClO3 is the limiting reactant.
The reaction uses 8 KClO3, so we have:
The thermochemical equation is:
Check Your Learning
When 1.42 g of iron reacts with 1.80 g of chlorine, 3.22 g of FeCl2(s) and 8.60 kJ of heat is produced. Calculate the standard reaction enthalpy change.
Answer:
ΔH = −339 kJ/mol
D26.4 Hess’s Law
Because enthalpy is a state function, the enthalpy change for a particular reaction is the same whether the reaction is carried out directly or is carried out as a series of steps. This enables calculation of the heat transfer of energy for a chemical change from other experimentally determined enthalpy changes. This type of calculation usually involves Hess’s law: If a process can be written as the sum of several stepwise processes, the enthalpy change of the total process equals the sum of the enthalpy changes of the various steps.
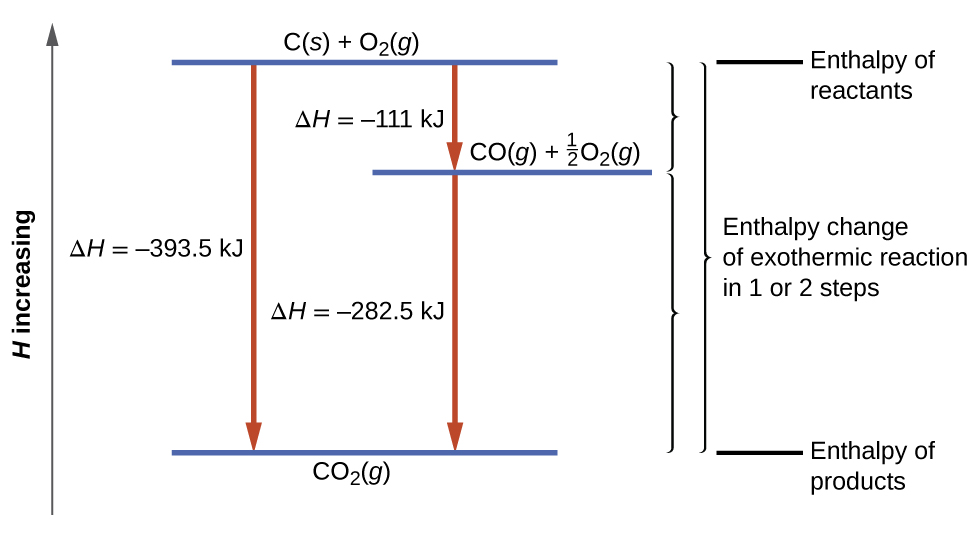
For example, we can think of the following reaction as occurring directly:
or in a two-step process:
[latex]\text{CO}(g) + \frac{1}{2} \;\text{O}_2 (g) \longrightarrow \text{CO}_2(g) \;\;\;\;\; \Delta _\text{r}H\text{°} = -283 \;\text{kJ}[/latex]
According to Hess’s law, the ΔrH° of the direct reaction equals the sum of the ΔrH° values of the steps. This is illustrated in Figure 5.
Example 9
Stepwise Calculation of [latex]\Delta _\text{r}H\text{°}[/latex] Using Hess’s Law
Determine the enthalpy of the reaction
from the enthalpy changes of the following two-step process:
Solution
We see that the reaction for which we want to find ΔrH° is the sum of the two reactions with known ΔrH° values, so to sum:
Check Your Learning
Calculate ΔrH° for the process:
from the following information:
Answer:
66.4 kJ/mol
Podia Question
Chlorine monofluoride can react with fluorine to form chlorine trifluoride:
(i) [latex]\text{ClF}(g) + \text{F}_2(g) \longrightarrow \text{ClF}_3(g) \;\;\;\;\; \Delta _\text{r}H\text{°}= \;?[/latex]
Use the reactions here to determine the ΔrH° for reaction (i):
(ii) [latex]2\text{OF}_2(g) \longrightarrow \text{O}_2(g) + 2\text{F}_2(g) \;\;\;\;\; \Delta _\text{r}H\text{°}_{(ii)} = -49.4 \;\text{kJ/mol}[/latex]
(iii) [latex]2\text{ClF}(g) + \text{O}_2(g) \longrightarrow \text{Cl}_2 \text{O}(g) + \text{OF}_2(g) \;\;\;\;\; \Delta _\text{r}H\text{°}_{(iii)} = +205.6 \;\text{kJ/mol}[/latex]
(iv) [latex]\text{ClF}_3(g) + \text{O}_2(g) \longrightarrow \frac{1}{2}\text{Cl}_2 \text{O}(g) + \frac{3}{2} \text{OF}_2(g) \;\;\;\;\; \Delta _\text{r}H\text{°}_{(iv)} = +266.7 \;\text{kJ/mol}[/latex]
Two days before the next whole-class session, this Podia question will become live on Podia, where you can submit your answer.

