Unit Three
Day 27: Enthalpy and Entropy
As you work through this section, if you find that you need a bit more background material to help you understand the topics at hand, you can consult “Chemistry: The Molecular Science” (5th ed. Moore and Stanitski) Chapter 16-1 through 16-5, and/or Chapter 11.5-11.6 and Chapter 12.1-12.5 in the Additional Reading Materials section.
D27.1 Standard State
Enthalpy changes are typically tabulated for reactions in which both the reactants and products are at the same conditions. A standard state is a commonly accepted set of conditions used as a reference point. For chemists, the standard state refers to materials under a pressure of 1 bar and solutions at a concentration of 1 M. The standard state does not specify a temperature. (Note that some thermochemical tables list values with a standard state of 1 atm. Because 1 bar = 0.987 atm, enthalpy change values are nearly the same under both sets of standard conditions.)
We will include a superscript “º” in the enthalpy change symbol to designate standard state. Thus, the symbol [latex]{\Delta}_\text{r}H^{\circ}_{\text {298 K}}[/latex] indicates an enthalpy change for a process occurring under standard-state conditions and at 298 K.
It is important to pay attention to the extensive nature of enthalpy and enthalpy changes. Since the enthalpy change for a given reaction is proportional to the amount of reaction that occurs, it may be reported on that basis (i.e., as the ΔrH for specific amounts of reactants). However, we often find it more useful to divide one extensive property (ΔrH) by another (amount of substance), and report a per-amount intensive value of ΔH, often “normalized” to a per-mole basis. (Note that this is similar to determining the intensive property specific heat capacity from the extensive property heat capacity.)
D27.2 Standard Formation Enthalpy
Standard formation enthalpy, [latex]\Delta _\text{f} H^\circ[/latex] is the enthalpy change for a reaction in which exactly one mole of a pure substance in a specified state (s, l, or g) is formed from free elements in their most stable states under standard-state conditions. The standard formation enthalpy is also referred to as the standard heat of formation.
The standard formation enthalpy of CO2(g) is −393.5 kJ/mol. This is the enthalpy change for the exothermic reaction:
starting with the reactants at a pressure of 1 bar and 25 °C (with the carbon present as graphite, the most stable form of carbon under these conditions) and ending with one mole of CO2, also at 1 bar and 25 °C.
For nitrogen dioxide, NO2(g), [latex]\Delta _\text{f}H^\circ[/latex] is 33.2 kJ/mol:
A reaction equation with ½ N2 and 1 O2 is appropriate in this case because the standard enthalpy of formation always refers to formation of 1 NO2(g).
By definition, the standard enthalpy of formation of an element in its most stable form is equal to zero under standard conditions. A table of standard formation enthalpies of many common substances in the Appendix.
Example 1
Evaluating a Standard Formation Enthalpy
Ozone, O3(g), forms from oxygen, O2(g), by an endothermic process. Ultraviolet radiation is the source of the energy that drives this reaction in the upper atmosphere. Assuming that both the reactants and products of the reaction are in their standard states, determine the standard enthalpy of formation, [latex]\Delta _\text{f}H^{\circ}[/latex] of ozone from the following information:
Solution
[latex]\Delta _\text{f}H^\circ[/latex] is the enthalpy change for the formation of one mole of a substance in its standard state from the elements in their standard states. Thus, [latex]\Delta _\text{f}H^\circ[/latex] for O3(g) is the enthalpy change for the reaction:
For the formation of 2 mol of O3(g), [latex]\Delta _{\text r}H^\circ_{298} = +286 \;\text{kJ/mol}[/latex]. Hence:
Therefore, [latex]\Delta _\text{f}H^\circ [\text{O}_3(g)] = +143 \;\text{kJ/mol}[/latex].
Check Your Learning
Hydrogen gas, H2, reacts explosively with gaseous chlorine, Cl2, to form hydrogen chloride, HCl(g). Calculate the enthalpy change for the reaction of 1 mole of H2(g) with 1 mole of Cl2(g) if both the reactants and products are at standard state conditions. The standard formation enthalpy of HCl(g) is −92.3 kJ/mol.
Answer:
For the reaction [latex]\text{H}_2(g) + \text{Cl}_2(g) \longrightarrow 2\text{HCl}(g) \;\;\;\;\; \Delta _\text{r}H^\circ_{\text{298 K}} = -184.6 \;\text{kJ/mol}[/latex]
Example 2
Writing Reaction Equations for [latex]\Delta _\text{f}H^\circ[/latex]
Write the formation enthalpy reaction equations for:
(a) C2H5OH(l)
(b) Ca3(PO4)2(s)
Solution
Remembering that [latex]\Delta _\text{f}H^\circ[/latex] reaction equations are for forming one mole of the compound from its constituent elements under standard-state conditions, we have:
(a) [latex]2\text{C}(s, \;\text{graphite}) + 3\text{H}_2(g) + \frac{1}{2} \text{O}_2(g) \longrightarrow \text{C}_2 \text{H}_5 \text{OH}(l)[/latex]
(b) [latex]3\text{Ca}(s) + \frac{1}{2} \text{P}_4(s) + 4\text{O}_2(g) \longrightarrow \text{Ca}_3 (\text{PO}_4)_2(s)[/latex]
Note: The standard state of carbon is graphite, and phosphorus exists as P4.
Check Your Learning
Write the standard heat of formation reaction equations for:
(a) C2H5OC2H5(l)
(b) Na2CO3(s)
Answer:
(a) [latex]4\text{C}(\text{s, graphite}) + 5\text{H}_2\text{(g)} + \frac{1}{2} \text{O}_2\text{(g)} \longrightarrow \text{C}_2 \text{H}_5 \text{O} \text{C}_2 \text{H}_5(l)[/latex];
(b) [latex]2\;\text{Na(s)} + \text{C}(\text{s, graphite}) + \frac{3}{2}\; \text{O}_2\text{(g)} \longrightarrow \text{Na}_2 \text{CO}_3\text{(s)}[/latex]
We can use Hess’s law to determine the enthalpy change of any reaction if the enthalpies of formation of the reactants and products are available. The stepwise reactions we consider are: decompositions of the reactants into their component elements, followed by re-combinations of the elements to give the products. The standard enthalpy change of the overall reaction is therefore equal to the sum of the standard enthalpies of formation of all the products minus the sum of the standard enthalpies of formation of all the reactants. Or:
Exercise 1: Using Standard Formation Enthalpies
Example 3
Using Hess’s Law
What is the standard enthalpy change for the reaction:
Solution:
Using the Equation:
Supporting Why the General Equation Is Valid
Alternatively, we can write this reaction as the sum of the decompositions of 3NO2(g) and 1H2O(l) into their constituent elements, and the formation of 2HNO3(aq) and 1NO(g) from their constituent elements. Writing out these reactions, and noting their relationships to the [latex]\Delta H^{\circ}_\text{f}[/latex] values for these compounds, we have:
Summing these reaction equations gives the reaction we are interested in:
Summing their enthalpy changes gives the value we want to determine:
So the standard enthalpy change for this reaction is ΔrH° = −138.4 kJ/mol.
Note that this result was obtained by (1) multiplying the [latex]\Delta _\text{f}H^{\circ}[/latex] of each product by its stoichiometric coefficient and summing those values, (2) multiplying the [latex]\Delta _\text{f}H^{\circ}[/latex] of each reactant by its stoichiometric coefficient and summing those values, and then (3) subtracting the result found in (2) from the result found in (1). This is also the procedure in using the general equation, as shown.
Check Your Learning
Calculate the heat of combustion of 1 mole of ethanol, C2H5OH(l), when H2O(l) and CO2(g) are formed.
C2H5OH(l) + 3O2(g) → 3H2O(l) + 2CO2(g)
Answer:
−1367 kJ/mol
D27.3 Entropy
In 1824, at the age of 28, Nicolas Léonard Sadi Carnot (Figure 1) published the results of an extensive study regarding the efficiency of steam heat engines. In a later review of Carnot’s findings, Rudolf Clausius introduced a new thermodynamic property that relates the spontaneous heat flow accompanying a process to the temperature at which the process takes place. This new property was expressed as the ratio of the reversible heat (qrev) and the kelvin temperature (T). The term reversible process refers to a process that takes place at such a slow rate that it is always at equilibrium and its direction can be changed (it can be “reversed”) by an infinitesimally small change in some condition.

In 1865, Clausius named this property entropy (S) and defined its change for any process as:
Similar to other thermodynamic properties, entropy is a state function, and ΔS depends only upon the initial and final states of a system. Hence, ΔS of a reaction is equal to the ΔS for the theoretical reversible process that involves the same initial and final states.
Following the work of Carnot and Clausius, Ludwig Boltzmann developed a molecular-scale statistical model that related the entropy of a system to the number of microstates (W) possible for the system:
Here k is the Boltzmann constant with a value of 1.38×10−23 J/K. A microstate is a specific configuration of the locations and energies of the atoms or molecules that comprise a system.
The change in entropy is then:
For processes involving an increase in the number of microstates, Wf > Wi, the entropy of the system increases, ΔS > 0. Conversely, processes that reduce the number of microstates, Wf < Wi, yield a decrease in system entropy, ΔS < 0. This molecular-scale interpretation of entropy provides a link to the probability that a process will occur.
D27.4 Predicting the Sign of ΔS
The relationships between entropy, microstates, and matter/energy dispersal allow us to make generalizations regarding the relative entropies of substances and to predict the sign of entropy changes for chemical and physical processes.
Consider the phase changes illustrated in Figure 2. In the solid phase, the molecules are restricted to nearly fixed positions with respect to each other and are capable of only modest oscillations about these positions; the number of microstates is relatively small. In the liquid phase, the molecules are free to move over and around each other, though they remain in relatively close proximity. This increased freedom of motion results in a greater variation in possible particle locations, so the number of microstates is correspondingly greater than for the solid. As a result, Sliquid > Ssolid and the process of converting a substance from solid to liquid (melting) is characterized by an increase in entropy, ΔS > 0.
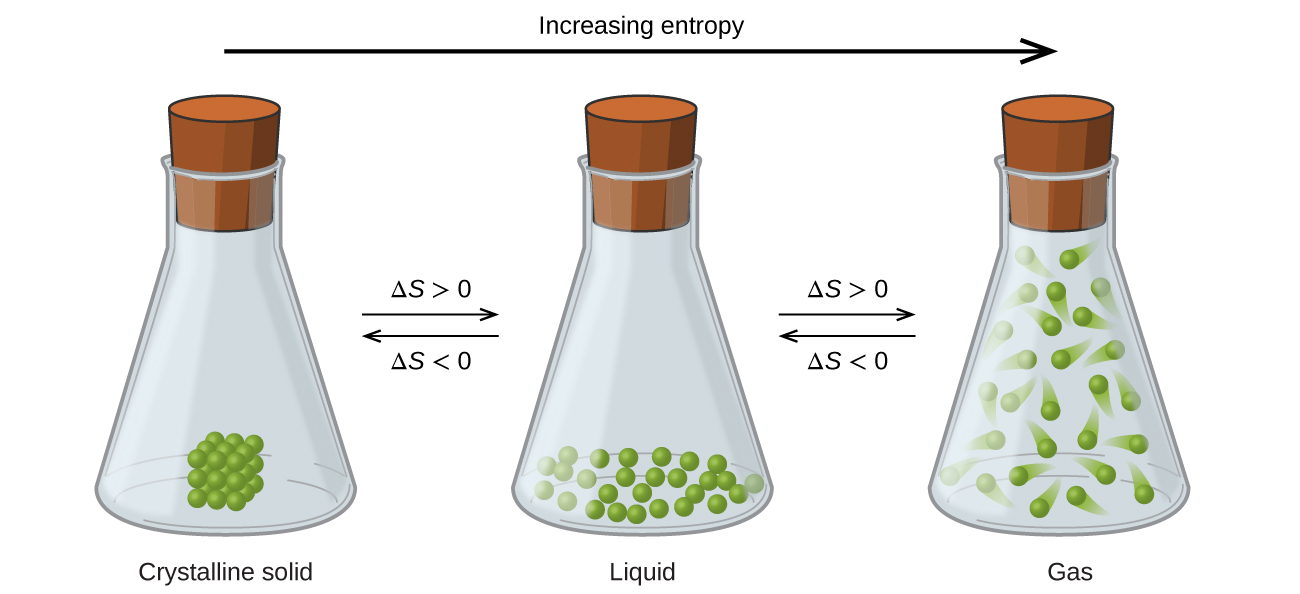
Solids and liquids have surfaces that define their volume, but in the gas phase the molecules occupy the entire container; therefore, for the same sample, each molecule in a gas can be found in many more locations (and there are many more microstates) than in the liquid or solid phase. Consequently, Sgas > Sliquid > Ssolid, and the processes of vaporization and sublimation involve increases in entropy, ΔS > 0.
At higher temperatures, the distribution of kinetic energies among the molecules of the substance is also broader (more dispersed) than at lower temperatures (Figure 3). Thus, the entropy for any substance increases with temperature.
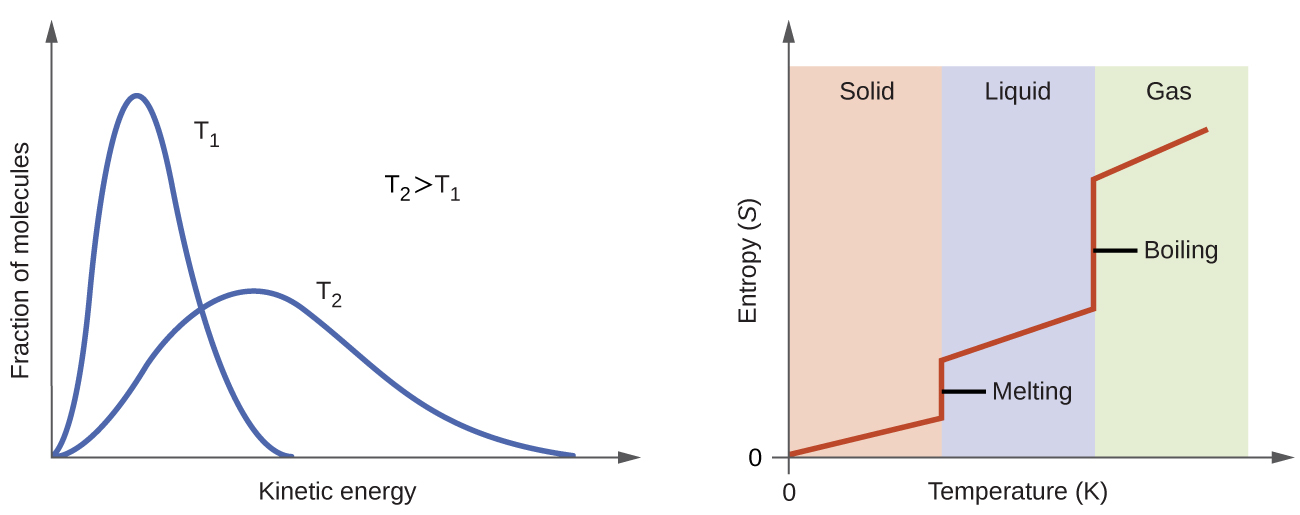
The entropy of a substance is also influenced by the structure of the particles that comprise the substance. With regard to atomic substances, heavier atoms possess greater entropy at a given temperature than lighter atoms, which is a consequence of the relation between a particle’s mass and the spacing of quantized translational energy levels. For molecules, greater numbers of atoms (regardless of their masses) within the molecule increase the ways in which the molecules can vibrate and thus increase the number of possible microstates and the system's entropy.
Finally, variations in the types of particles affects the entropy of a system. Compared to a pure substance, in which all particles are identical, the entropy of a mixture of different particle types is greater due to the additional orientations and interactions that are possible. For example, when a solid dissolves in a liquid, the particles of the solid experience both a greater freedom of motion and additional interactions with the solvent particles. This corresponds to a more uniform dispersal of matter and energy and a greater number of microstates. The process of dissolution therefore involves an increase in entropy, ΔS > 0.
Exercise 2: Predicting Entropy Changes
For each change below, indicate whether the entropy of the system increases, decreases or stays the same.
Example 5
Predicting the Sign of ∆S
Predict the sign of the entropy change for each process. Indicate the reason for each of your predictions.
(a) One mole liquid water at room temperature [latex]\longrightarrow[/latex] one mole liquid water at 50 °C
(b) I2(g) + Cl2(g) [latex]\longrightarrow[/latex] 2 ICl(g)
(c) [latex]\text{C}_6\text{H}_6(l)\;+\;\frac{15}{2}\text{O}_2(g)\;{\longrightarrow}\;6\text{CO}_2(g)\;+\;3\text{H}_2\text{O}(l)[/latex]
(d) [latex]\text{NH}_3(s)\;{\longrightarrow}\;\text{NH}_3(l)[/latex]
Solution
(a) positive, temperature increases
(b) positive, same number of gas molecules before and after but molecules are sightly more complex in product
(c) negative, net decrease in the amount of gaseous species
(d) positive, phase transition from solid to liquid, net increase in dispersal of matter
Check Your Learning
Predict the sign of the enthalpy change for the following processes. Give a reason for your prediction.
(a) [latex]\text{NaNO}_3(s)\;{\longrightarrow}\;\text{Na}^{+}(aq)\;+\;\text{NO}_3^{\;\;-}(aq)[/latex]
(b) the freezing of liquid water
(c) [latex]\text{CO}_2(s)\;{\longrightarrow}\;\text{CO}_2(g)[/latex]
(d) [latex]\text{CaCO}(s)\;{\longrightarrow}\;\text{CaO}(s)\;+\;\text{CO}_2(g)[/latex]
Answer:
(a) Positive; The solid dissolves to give an increase of mobile ions in solution. (b) Negative; The liquid becomes a more ordered solid. (c) Positive; The relatively ordered solid becomes a gas. (d) Positive; There is a net production of one mole of gas.
D27.5 Second Law of Thermodynamics
For some chemical reactions, reactants are converted mainly to products. In a product-favored reaction, the kinetics of the conversion may be slow, but given enough time the reaction mixture becomes mainly products. For other chemical reactions, called reactant-favored processes, no matter how long one waits, the reaction mixture consists mainly of reactants. It is useful to be able to predict whether a process is reactant-favored or product-favored. The second law of thermodynamics enables such predictions.
In thermodynamic models, the system and surroundings comprise everything, that is, the universe, and so the following is true:
To illustrate this relation, consider the process of heat transfer of energy between two objects, one identified as the system and the other as the surroundings. There are three possibilities for such a process:
- The objects are at different temperatures, and energy transfers from the hotter to the cooler object. This is always observed to occur. Designating the hotter object as the system and invoking the definition of entropy yields
[latex]{\Delta}S_{\text{sys}} = \dfrac{-q_{\text{rev}}}{T_{\text{sys}}}\;\;\;\;\;\;\;\text{and}\;\;\;\;\;\;\;{\Delta}S_{\text{surr}} = \dfrac{q_{\text{rev}}}{T_{\text{surr}}}[/latex]
The arithmetic signs of qrev denote the loss of heat by the system and the gain of heat by the surroundings. Since Tsys > Tsurr in this scenario, the magnitude of the entropy change for the surroundings is positive and greater than the negative entropy chage for the system. Thus, ΔSsys and ΔSsurr sum to a positive value for ΔSuniv. This process involves an increase in the entropy of the universe.
- The objects are at different temperatures, and heat flows from the cooler to the hotter object. This is never observed to occur. Again designating the hotter object as the system:
[latex]{\Delta}S_{\text{sys}} = \dfrac{q_{\text{rev}}}{T_{\text{sys}}}\;\;\;\;\;\;\;\text{and}\;\;\;\;\;\;\;{\Delta}S_{\text{surr}} = \dfrac{-q_{\text{rev}}}{T_{\text{surr}}}[/latex]
The magnitude of the entropy change for the surroundings is again greater than that for the system, but in this case, the signs of the entropy change for the surroundings is negative, yielding a negative value for ΔSuniv. This process involves a decrease in the entropy of the universe. (Note also that possibility 1, which is the reverse of this process, always occurs.)
- The temperature difference between the objects is infinitesimally small, Tsys ≈ Tsurr, and so the heat transfer of energy is thermodynamically reversible. In this case, the system and surroundings experience entropy changes that are equal in magnitude and therefore sum to a value of zero for ΔSuniv. This process involves no change in the entropy of the universe.
These results lead to a profound statement regarding the relation between entropy and spontaneity known as the second law of thermodynamics: all changes that take place of their own accord (are product-favored) involve an increase in the entropy of the universe.
| ΔSuniv > 0 | product-favored (takes place of its own accord) |
| ΔSuniv < 0 | reactant-favored (reverse reaction would occur) |
| ΔSuniv = 0 | no reaction in either direction (system is at equilibrium) |
For many realistic applications, the surroundings are vast in comparison to the system. In such cases, the heat transfer of energy to or from the surroundings as a result of some process is a very small, nearly infinitesimal, fraction of its total thermal energy. For example, combustion of a hydrocarbon fuel in air involves heat transfer of energy from a system (the fuel and oxygen molecules reacting to form carbon dioxide and water) to surroundings that are infinitely more massive (Earth’s atmosphere). As a result, qsurr is a good approximation of qrev, and the second law may be stated as
We can use this equation to predict whether a process is product-favored.
Example 6
At What Temperatures Does Ice Melt?
The entropy change for the process
is 22.1 J/K mol and requires that the system be heated by 6.00 kJ/mol. Is the process product-favoredat −10.00 °C? Is it product-favored at +10.00 °C?
Solution
We can assess the spontaneity of the process by calculating the entropy change of the universe. If ΔSuniv is positive, then the process is spontaneous. At both temperatures, ΔSsys = 22.1 J/K mol and qsurr = −6.00 kJ/mol.
At −10.00 °C (263.15 K):
ΔSuniv < 0, so melting is reactant-favored at −10.0 °C.
At 10.00 °C (283.15 K):
ΔSuniv > 0, so melting is product-favored at 10.00 °C.
Check Your Learning
Using this information, determine whether liquid water will spontaneously freeze at the same temperatures. What can you say about the values of ΔSuniv?
Answer:
At −10.00 °C product-favored, ΔSuniv = +0.7 J/K mol; at +10.00 °C reactant-favored, ΔSuniv = −0.9 J/K mol. (Entropy is a state function, and freezing is the opposite of melting. )
D27.6 Third Law of Thermodynamics
Consider the entropy of a pure, perfectly crystalline solid possessing no kinetic energy (that is, at a temperature of absolute zero, 0 K). This system may be described by a single microstate, as its purity, perfect crystallinity and complete lack of motion means there is but one possible location for each identical molecule comprising the crystal (W = 1). According to the Boltzmann equation, the entropy of this system is zero.
This limiting condition for a system’s entropy represents the third law of thermodynamics: the entropy of a pure, perfect crystalline substance at 0 K is zero.
We can make careful calorimetric measurements to determine the temperature dependence of a substance’s entropy and to derive absolute entropy values under specific conditions. Standard entropies (S°) are determined for 1 mole of substance at a pressure of 1 bar. The standard entropy change (ΔrS°) for any chemical process may be computed from the standard entropies of its reactant and product species:
For example, ΔrS° for the reaction
is:
The thermodynamics table in the appendix lists some standard entropies at 298.15 K.
Example 7
Determination of ΔrS°
Calculate the standard entropy change for this reaction:
Solution
The value of the standard entropy change at room temperature, [latex]{\Delta}_{\text{r}}S_{298}^{\circ}[/latex], is the difference between the standard entropy of the product, H2O(l), and the standard entropy of the reactant, H2O(g).
The value for [latex]{\Delta}S_{298}^{\circ}[/latex] is negative, as expected for this phase transition (condensation) at room temperature.
Check Your Learning
Calculate the standard entropy change for this process:
Answer:
−120.6 J mol−1 K−1
Example 8
Determination of ΔS°
Calculate the standard entropy change for the combustion of methanol, CH3OH, at 25 °C.
Solution
The value of the standard entropy change is equal to the difference between the standard entropies of the products and the standard entropies of the reactants scaled by their stoichiometric coefficients.
Check Your Learning
Calculate the standard entropy change for this reaction:
Answer:
26.3 J/mol·K
Suppose an exothermic chemical reaction takes place at constant atmospheric pressure. There is a heat transfer of energy from the reaction system to the surroundings. The energy transfer to the surroundings equals the energy transfer from the reaction but has the opposite sign because the transfer is in the opposite direction. The heat transfer of energy for the system is the enthalpy change of the reaction because, at constant pressure, ΔrH° = qp (Section D26.3). Because the energy transfer to the surroundings is reversible, the entropy change for the surroundings can also be calculated from:
The same reasoning applies to an endothermic reaction: qsys and qsurr are equal but have opposite sign. Also, for a chemical reaction system, ΔSsys = ΔrS°, the standard entropy change for the reaction. Hence, ΔSuniv can be expressed as:
The convenience of this equation is that for a given reaction the enthalpy change of the universe can be calculated from thermodynamic data for the system only. That is, from data in the Appendix.
Podia Question
Use data from the Appendix to calculate ΔrS° for this reaction at 298 K:
2 NO(g) + O2(g) → 2 NO2(g)
colorless gas colorless gas → red-brown gas
Predict whether the reaction is product-favored.
Now, watch this video in which NO(g) is added to O2(g) in a flask. Does the video validate your prediction? Explain why or why not.
If the video does not validate your prediction, try to figure out why your prediction did not work and re-do the it in a different way.
If the video does validate your prediction, explain what thermodynamic aspect of the reaction accounts for the observations in the video.
Two days before the next whole-class session, this Podia question will become live on Podia, where you can submit your answer.

