Unit Three
Day 28: Gibbs Free Energy, Chemical Equilibrium
As you work through this section, if you find that you need a bit more background material to help you understand the topics at hand, you can consult “Chemistry: The Molecular Science” (5th ed. Moore and Stanitski) Chapter 16-6, 12-1 and 12-2, and/or Chapter 12.6-12.8 and Chapter 13.1-13.3 in the Additional Reading Materials section.
D28.1 Gibbs Free Energy
One of the challenges of using the second law of thermodynamics to determine if a process proceeds forward of its own accord is that we must determine ΔSsystem and ΔSsurroundings. An alternative approach involving a new thermodynamic property was introduced in the late 19th century by American mathematician Josiah Willard Gibbs. The property is called the Gibbs free energy (G) (or simply the free energy), and is defined in terms of a system’s enthalpy, entropy, and temperature:
Because H, T, and S are state functions, G must also be a state function. The change in Gibbs free energy (ΔG) at constant temperature may be expressed as:
Gibbs free energy change is related to whether a process proceeds forward of its own accord. This can be derived from the second law expression:
Multiplying both sides of this equation by −T, and rearranging yields:
Hence:
For a process that proceeds forward ΔSuniv must be positive. Because thermodynamic temperature is always positive, the Gibbs free energy change must be negative for a process that proceeds forward of its own accord.
| ΔSuniv > 0 | ΔG < 0 | proceeds forward of its own accord |
| ΔSuniv < 0 | ΔG > 0 | reverse process proceeds of its own accord |
| ΔSuniv = 0 | ΔG = 0 | at equilibrium |
D28.2 Calculating ΔG
Because Gibbs free energy is a state function, its value depends only on the conditions of the initial and final states of the system. A convenient and common approach to calculate ΔG for reactions is by using standard state thermodynamic data. One method involves using the definition of ΔG given above but restricting to standard-state conditions:
Example 1
Evaluation of ΔG° Change from ΔH° and ΔS°
Use standard enthalpy and entropy data from the Appendix to calculate the standard Gibbs free energy change for the vaporization of water at room temperature (298 K). Based on the value for ΔG° is this process product favored?
Solution
The process is:
From Appendix, the data are:
| Substance | [latex]{\Delta} _{\text{f}}H^{\circ}(\text{kJ/mol})[/latex] | [latex]S^{\circ}(\text{J/K}{\cdot}\text{mol})[/latex] |
|---|---|---|
| H2O(l) | −285.83 | 69.9 |
| H2O(g) | −241.82 | 188.8 |
At 298 K:
and:
Converting ΔrS into kJ/mol·K and combining:
At 298 K (25 °C) [latex]{\Delta}_{\text{r}}G^{\circ}\;{\text >}\;0[/latex], therefore boiling is not product-favored.
Check Your Learning
Use standard enthalpy and entropy data from the Appendix to calculate the standard Gibbs free energy change for the reaction shown below at 298 K. Based on the computed value for ΔrG°, is this process product-favored?
Answer:
[latex]{\Delta}_{\text{r}}G^{\circ} = 101\;\text{kJ/mol}[/latex]; the reaction is reactant-favored at 25 °C.
It is also possible to use the standard Gibbs free energy of formation ([latex]{\Delta}G_{\text{f}}^{\circ}[/latex]) for each of the reactants and products involved in the reaction to calculate Gibbs free energy changes. [latex]{\Delta}_{\text{f}}G^{\circ}[/latex] is the Gibbs free energy change that accompanies the formation of one mole of a substance from its elements in their standard states. [latex]{\Delta}G_{\text{f}}^{\circ}[/latex] is by definition zero for elemental substances under standard state conditions.
For a reaction:
the standard Gibbs free energy change at room temperature is:
Exercise 1: Calculating Standard Gibbs Free Energy Change
Example 2
Calculation of [latex]{\Delta}_{\text{r}}G_{298}^{\circ}[/latex]
Consider the decomposition of yellow mercury(II) oxide.
Calculate [latex]{\Delta}_{\text{r}}G_{298}^{\circ}[/latex] using (a) standard Gibbs free energies of formation and (b) standard enthalpies of formation and standard entropies. Is the reaction product-favored or reactant-favored under these conditions?
Solution
The required data are available in the Appendix and are shown here.
| Compound | [latex]{\Delta}G_{\text{f}}^{\circ}(\text{kJ/mol})[/latex] | [latex]{\Delta}H_{\text{f}}^{\circ}(\text{kJ/mol})[/latex] | [latex]S_{298}^{\circ}(\text{J/K}{\cdot}\text{mol})[/latex] |
|---|---|---|---|
| HgO (s, yellow) | −58.54 | −90.83 | 70.29 |
| Hg(l) | 0 | 0 | 76.02 |
| O2(g) | 0 | 0 | 205.1 |
(a) Using Gibbs free energies of formation:
(b) Using standare formation enthalpies and standard entropies:
Both calculations yield the same numerical value (to three significant figures), and both predict that the process is reactant-favored at room temperature.
Check Your Learning
Calculate ΔrG° using (a) Gibbs free energies of formation and (b) standard formation enthalpies and standard entropies (Appendix). Do the results indicate the reaction to be product-favored or reactant-favored at 25 °C?
Answer:
ΔrG° = 141.1 kJ/mol, reactant favored
D28.3 Temperature Dependence
Consider:
Whether a reaction is product-favored, as reflected in the arithmetic sign of its ΔrG°, is determined by the signs of ΔrH° and ΔrS°, and, in some cases, the absolute temperature (which can only have positive values). Four possibilities therefore exist:
- Both ΔrH° and ΔrS° are positive. This condition describes an endothermic process that involves an increase in system entropy. In this case, ΔrG° will be negative if the magnitude of the TΔrS° term is greater than ΔrH°, and positive if the TΔrS° term is less than ΔrH°. Such a process is product-favored at high temperatures and reactant-favored at low temperatures.
- Both ΔrH° and ΔrS° are negative. This condition describes an exothermic process that involves a decrease in system entropy. In this case, ΔrG° will be negative if the magnitude of the TΔrS° term is less than ΔrH° and positive if the TΔrS° term is greater than ΔrH°. Such a process is product-favored at low temperatures and reactant-favored at high temperatures.
- ΔrH° is positive and ΔrS° is negative. This condition describes an endothermic process that involves a decrease in system entropy. In this case, ΔrG° will be positive regardless of the temperature. Such a process is reactant-favored at all temperatures.
- ΔrH° is negative and ΔrS° is positive. This condition describes an exothermic process that involves an increase in system entropy. In this case, ΔrG° will be negative regardless of the temperature. Such a process is product-favored at all temperatures.
These four scenarios are summarized in Figure 1.

Example 3
Predicting whether a reaction is product-favored at different temperatures
The incomplete combustion of carbon is described by this equation:
How does temperature affect whether the process is product-favored?
Solution
Combustion processes are exothermic (ΔrH° < 0). This particular reaction involves an increase in entropy due to the accompanying increase in the amount of gaseous species (net gain of one mole of gas, ΔrS° > 0). The reaction is therefore product-favored (ΔrG° < 0) at all temperatures.
Check Your Learning
Popular chemical hand warmers generate heat by the air oxidation of iron:
How does temperature affect whether the process is product-favored?
Answer:
ΔrH° and ΔrS° are negative; the reaction is product-favored at low temperatures.
A process that is reactant-favored at one temperature but product-favored at a different temperature must have some temperature where it changes from reactant-favored to product-favored (as reflected by the sign of its ΔrG°). This is illustrated graphically in Figure 2, where ΔrG° is plotted on the y axis versus T on the x axis :
A process whose ΔrH° and ΔrS° have the same arithmetic sign becomes more or less product-favored depending on temperature as depicted by the two yellow lines in the plot. Each line crosses from product-favored to reactant-favored at a temperature that is characteristic of the specific process. This temperature is represented by the x-intercept of the line—the value of T for which ΔrG° is zero:
And so, saying a process is product-favored at “high” or “low” temperatures means the temperature is above or below, respectively, that temperature at which ΔrG° for the process is zero.
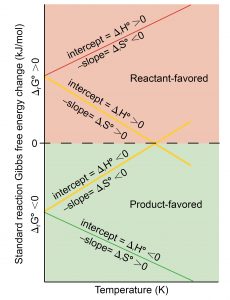
Example 4
Equilibrium Temperature for a Phase Transition
The boiling point of a liquid is the temperature at which its solid and liquid phases are in equilibrium (when vaporization and condensation occur at equal rates) where ΔrG = 0. The normal boiling point is the boiling point at 1 bar pressure, which corresponds to the standard-state difference ΔrG° = 0. Use information in the Appendix to estimate the boiling point of water.
Solution
The process of interest is this phase change:
When ΔrG° = 0:
Using the standard thermodynamic data from the Appendix,
The accepted value for water’s normal boiling point is 373.2 K (100.0 °C), and so this calculation is in reasonable agreement. Note that the values for enthalpy and entropy changes were derived from standard data at 298 K (Appendix). If desired, you could obtain more accurate results by using enthalpy and entropy changes determined at (or at least closer to) the actual boiling point.
Check Your Learning
Use information in the Appendix to estimate the boiling point of CS2.
Answer:
320 K (accepted value 319 K)
D28.4 Chemical Equilibrium
A chemical reaction is usually written in a way that suggests it proceeds in one direction, the direction in which we read, but all chemical reactions are reversible: both the forward and reverse reaction occur at the same time. When reactions involve gases or solutions, where concentrations change as the reaction proceeds, the reaction eventually reaches a dynamic equilibrium. In a chemical equilibrium, the forward and reverse reactions occur at equal rates, and the concentrations of products and reactants remain constant. This implies that, if a reaction occurs in a closed system so that the products cannot escape, the reaction often does not yield 100% products. Instead, some reactants remain after the concentrations stop changing. At this point, when there is no further change in concentrations of reactants and products, we say the reaction is at equilibrium.
For example, when we place a sample of dinitrogen tetraoxide (N2O4, a colorless gas) in a glass tube, the color becomes darker as N2O4 is converted to nitrogen dioxide (NO2, a red-brown gas) by the reaction:
The double arrow, ⇌, indicates that the products react to form reactants as well as the reactants producing products. When the system reaches equilibrium, both N2O4 and NO2 are present (Figure 3).
![A three-part diagram is shown. At the top of the diagram, three beakers are shown, and each one contains a sealed tube. The tube in the left beaker is full of a colorless gas which is connected to a zoom-in view of the particles in the tube by a downward-facing arrow. This particle view shows seven particles, each composed of two connected blue spheres. Each blue sphere is connected to two red spheres. The tube in the middle beaker is full of a light brown gas which is connected to a zoom-in view of the particles in the tube by a downward-facing arrow. This particle view shows nine particles, five of which are composed of two connected blue spheres. Each blue sphere is connected to two red spheres. The remaining four are composed of two red spheres connected to a blue sphere. The tube in the right beaker is full of a brown gas which is connected to a zoom-in view of the particles in the tube by a downward-facing arrow. This particle view shows eleven particles, three of which are composed of two connected blue spheres. Each blue sphere is connected to two red spheres. The remaining eight are composed of two red spheres connected to a blue sphere. At the bottom of the image are two graphs. The left graph has a y-axis labeled, “Concentration,” and an x-axis labeled, “Time.” A red line labeled, “N O subscript 2,” begins in the bottom left corner of the graph at a point labeled, “0,” and rises near the highest point on the y-axis before it levels off and becomes horizontal. A blue line labeled, “N subscript 2 O subscript 4,” begins near the highest point on the y-axis and drops below the midpoint of the y-axis before leveling off. The right graph has a y-axis labeled, “Rate,” and an x-axis labeled, “Time.” A red line labeled, “k subscript f, [ N subscript 2 O subscript 4 ],” begins in the bottom left corner of the graph at a point labeled, “0,” and rises near the middle of the y-axis before it levels off and becomes horizontal. A blue line labeled, “k subscript f, [ N O subscript 2 ] superscript 2,” begins near the highest point on the y-axis and drops to the same point on the y-axis as the red line before leveling off. The point where both lines become horizontal is labeled, “Equilibrium achieved.”](https://wisc.pb.unizin.org/app/uploads/sites/290/2019/04/D28_Fig03-Revised-300x242.jpg)
Consider the example in Figure 3. Not only can N2O4 decompose to form NO2, but the NO2 produced can react to form N2O4. As soon as the forward reaction produces any NO2, the reverse reaction begins and NO2 starts to react to form N2O4. As the reaction proceeds the rate of the forward reaction decreases and the rate of the reverse reaction increases. (The forward reaction is first order and as concentration of N2O4 decreases the forward rate decreases. The reverse reaction is second order; as concentration of NO2 increases the rate also increases.) At equilibrium, the concentrations of N2O4 and NO2 no longer change because the rate of NO2 formation is exactly equal to the rate of NO2 consumption, and the rate of formation of N2O4 is exactly equal to the rate of consumption of N2O4. Chemical equilibrium is a dynamic process: the numbers of reactant and product molecules remain constant, but the forward and reverse reactions do not stop.
We use an equilibrium arrow when writing an equation for a reversible reaction. Such a reaction may or may not be at equilibrium. When we wish to speak about one particular component of a reversible reaction, we use a single arrow. For example, in the equilibrium shown in Figure 3, the rate of the forward reaction
is equal to the rate of the backward reaction
An equilibrium can be established for a physical change as well as for a chemical reaction. For example:
Figure 4 shows a sample of liquid bromine at equilibrium with bromine vapor in a closed container. When we pour liquid bromine into an empty bottle in which there is no bromine vapor, some liquid evaporates: the amount of liquid decreases and the amount of vapor increases. If we seal the container so no vapor escapes, the amount of liquid and vapor will eventually stop changing and an equilibrium between the liquid and the vapor will be established. If the container were not sealed, the bromine vapor would escape and no equilibrium would be reached.

D28.5 Equilibrium Constants
An equilibrium constant (K) is a ratio of equilibrium concentrations of products and reactants that remains constant for a given reaction at a given temperature. For example, consider this general equation for a reversible reaction:
For this reaction, the concentration equilibrium constant, Kc, is equal to the molar concentrations of the products, each raised to the power of the coefficient in the equation and all multiplied together, divided by the molar concentrations of the reactants, each raised to the power of its coefficient and all multiplied together:
This mathematical expression is called the equilibrium constant expression. Square brackets indicate equilibrium concentrations of reactants and products.
Because each concentration has units mol/L, an equilibrium constant can have units depending on the coefficients in the chemical equation. For example, the equilibrium constant for the N2O4 reaction described earlier has units mol/L because the concentration in the numerator is squared but the denominator is not. However, the equilibrium constant for reaction of H2 and I2 to form 2 HI has no units because the sum of exponents in the numerator of the equilibrium constant expression for this reaction equals the sum of exponents in the denominator.
N2O4(g) ⇌ 2 NO2(g) Kc = [latex]\dfrac{[\text{NO}_2]^2}{[\text{N}_2\text{O}_4]}[/latex] units mol/L
H2(g) + I2(g) ⇌ 2 HI(g) Kc = [latex]\dfrac{[\text{H}_2][\text{I}_2]}{[\text{HI}]^2}[/latex] units cancel so Kc is unitless
Units are often omitted when evaluating equilibrium constants because it is easy to tell what units are needed from the mathematical form of the equilibrium constant expression.
Reaching equilibrium requires that concentrations of reactants and products change until the rates of forward and reverse reactions are equal. Therefore, only substances whose concentrations change as a reaction occurs are included in an equilibrium constant expression. For example, consider this equilibrium:
2 HgO(s) ⇌ 2 Hg(l) + O2(g) Kc = [O2]
Because HgO is a pure solid, the number of HgO formula units in a given volume of HgO is the same throughout the reaction; it depends only on the density of HgO at the temperature of the reaction. Similarly, the number of Hg atoms per unit volume of pure Hg(l) is constant throughout the reaction. Thus, these concentrations are not included in the equilibrium constant expression. It is necessary for some HgO(s) and some Hg(l) to be present for the equilibrium to be maintained, but the quantity of each does not matter. In general, Kc expressions do not contain terms for pure solids or pure liquids.
For dilute solutions, the concentration of solvent remains constant throughout an equilibrium reaction and is not included in the equilibrium constant expression, even though the solvent may appear in the reaction equation.
A homogeneous equilibrium is one in which all of the reactants and products are present in a single phase (are all in a solution, which, by definition, is a homogeneous mixture). Examples of homogeneous equilibria are reactions in the gas phase and reactions in liquid solutions. For example:
In these aqueous equilibrium systems, H2O(l) is the solvent. Its concentration does not appear in the Kc expression.
A heterogeneous equilibrium is a system in which reactants and products are found in two or more phases. Some heterogeneous equilibria involve chemical changes, for example:
Other heterogeneous equilibria involve phase changes, for example:
The equilibrium constant expression is different if a reaction changes stoichiometry, is reversed, or is the sum of several steps. The value of the equilibrium constant therefore changes.
When all the coefficients in a balanced chemical equation are multiplied by some factor n, then the new equilibrium constant is the original equilibrium constant raised to the nth power. For example:
When a reaction’s direction is reversed, the equilibrium constant for the new reaction is simply the reciprocal (inverse) of that for the original reaction. For example:
When two reactions are added together to obtain a new reaction, the equilibrium constant for the new reaction is the product of the equilibrium constants for the original reactions. For example:
Exercise 2: Properties of Chemical Equilibrium
Podia Question
One way to remove silver oxide tarnish from silver is to heat the silver to a high temperature. For example, see this video. The reaction is
2 Ag2O → 4 Ag(s) + O2(g)
At 298 K, the reaction is reactant-favored. Obtain data from the Appendix and determine at what temperature the reaction becomes product-favored. What assumption needs to be made to solve this problem?
Two days before the next whole-class session, this Podia question will become live on Podia, where you can submit your answer.

