As you work through this section, if you find that you need a bit more background material to help you understand the topics at hand, you can consult “Chemistry: The Molecular Science” (5th ed. Moore and Stanitski) Chapter 12-6 and 12-7, and/or Chapter 14.1-14.6 in the Additional Reading Materials section.

Le Châtelier’s principle states that when a chemical system is at equilibrium and conditions are changed so that the reaction quotient, Q, changes, the chemical system will react to achieve new equilibrium concentrations or partial pressures; reaction occurs in a way that partially counteracts the change in conditions. To establish the new equilibrium, the reaction proceeds in the forward direction if Q < K or in the reverse direction if Q > K until Q is again equal to K.

D30.1 Change in Concentration

For a chemical system at equilibrium at constant temperature, if the concentration of a reactant or the concentration of a product is changed and Q also changes, the system is no longer at equilibrium because Q ≠ K. The concentrations of both reactants and products then undergo additional changes until the system reaches a new equilibrium with different equilibrium concentrations. We say that the equilibrium shifts in a direction (forward or reverse) that partially counteracts the change.

For example, consider the equilibrium of the chemical reaction:

A mixture of gases at 400 °C with [H₂] = [I₂] = 0.221 M and [HI] = 1.563 M is at equilibrium. For this mixture, Q_c = K_c = 50.0. If H₂ is introduced into the system quickly such that its concentration doubles before it begins to react (new [H₂] = 0.442 M), Q_c is now ½ of K_c:

The reaction proceeds in the forward direction to reach a new equilibrium, at which [H₂] = 0.374 M, [I₂] = 0.153 M, and [HI] = 1.692 M. Notice that the new equilibrium concentration of H₂, 0.374 M, is less than the doubled concentration (0.442 M) but more than the concentration at the first equilibrium (0.221 M). The equilibrium has shifted to partially counteract the change. Because of the shift, the concentration of the other reactant decreases and the concentration of the product increases. To verify that these new concentrations are equilibrium concentrations, calculate Q:

Another way to think about the shift in equilibrium is to recall that at equilibrium, rate_forward = rate_reverse). The forward reaction is first-order in H₂ (and first-order in I₂), so doubling the concentration of H₂ doubles the rate, making rate_forward > rate_reverse. As the equilibrium shifts the concentrations of both reactants decrease and the concentration of product increases until new equilibrium concentrations are reached where forward and reverse reactions have reached new,  but equal rates.

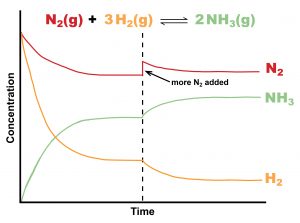
Figure 1 illustrates graphically the effect of adding N₂ to the N₂(g) + 3H₂(g) ⇌ 2NH₃(g) equilibrium, an important equilibrium in the chemical industry know as the Haber-Bosch process.

D30.2 Change in Pressure or Volume

Changes in pressure have a measurable effect on equilibrium in systems involving gases if the chemical reaction produces a change in the total number of gas molecules; that is, if there is a different number of gas molecules on the reactant side from the product side of the equation. The overall change in pressure must affect partial pressures of reactants and/or products: Adding an inert gas that is not a reactant or product changes the total pressure but not the partial pressures of the gases in the equilibrium constant expression, and therefore does not perturb the equilibrium.

Consider what happens when  the volume decreases for this equilibrium:

Decreasing the volume increases the total pressure and increases the partial pressure of each gas. The equilibrium shifts to partially counteract the increase in pressure. Formation of additional NO₂ decreases the total number of gaseous molecules in the system because each time two molecules of NO₂ form, a total of three molecules of NO and O₂ react away. This reduces the total pressure exerted by the system and partially counteracts increased pressure. LeChatelier’s principle predicts that reaction shifts right, toward products.

We can also look at this by considering the reaction quotient. Reducing the system volume increases the partial pressure (or concentration) of all gaseous species. If the volume is reduced by half, then each partial pressure becomes twice what it was for the previous equilibrium:

Because Q_c < K_c, the reaction proceeds toward the product side (forming additional NO₂) to re-establish equilibrium.

Now consider this reaction:

Because there is no change in the total number of gaseous molecules in the system during reaction, a change in pressure does not favor either formation or decomposition of NO.

Similarly, for reactions in solution, changing the solution volume changes the concentrations of all reaction species. Therefore, when solvent is added (the solution is diluted), the equilibrium shifts toward the side with more solute particles, partially compensating for the dilution of total concentration. If solvent is removed (by evaporation, for example) so that all solute concentrations increase, the equilibrium shifts toward the side with fewer solute particles, decreasing the total concentration of solute particles.

For example, when enough water is added to this equilibrium to double the solution volume,

the concentration of each solute is halved compared to the initial equilibrium concentration. Hence:

Because Q_c > K_c the reaction proceeds toward the reactant side (the side with more solute particles) as equilibrium is re-established.

D30.3 Change in Temperature

When temperature changes, the equilibrium constant changes. Predicting whether K increases or decreases enables us to predict which way an equilibrium shifts when temperature increases. For example, consider this generic reaction at equilibrium:

reactant ⇌ product

Hence:

The rate constants increase with increasing temperature, as described by the Arrhenius equation (Section D23.1). The bigger the activation energy, E_a, is the greater the effect of temperature on the rate constant is.

If the E_a is greater for the forward reaction than for the reverse reaction, k_forward increases more rapidly with increasing temperature than does k_reverse. Because K_c = [latex]\frac{[k_{\text{forward}}]}{[k_{\text{reverse}}]}[/latex], K_c increases as T increases, and at higher T more product is formed: the reaction shifts right. This corresponds to an endothermic reaction. If, on the other hand, the activation energy (E_a) is greater for the reverse reaction than for the forward reaction, k_reverse increases more rapidly with increasing temperature than does k_forward, K_c decreases as T increases, and at higher T there is more reactant: the reaction shifts left. This corresponds to an exothermic reaction. These two cases are shown in Figure 2.

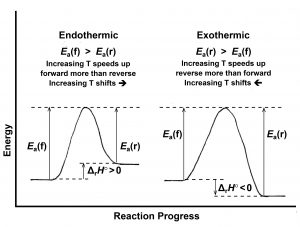
Thus, for an endothermic reaction, as temperature increases, the forward rate becomes greater than the reverse rate and product forms more rapidly. Product concentration increases. Eventually the higher product concentration increases the reverse rate and the lower reactant concentration decreases the forward rate until the rates become equal again. A new equilibrium is established with a higher ratio of product to reactant concentrations; that is, with a larger K_c. The endothermic reaction shifts right with increasing temperature.

D30.4 Catalysts

A catalyst speeds up the rate of a reaction, allowing the equilibrium to be reached more quickly (by speeding up the forward and reverse reactions). Hence, catalysts influence the kinetics of a reaction. However, a catalyst has no effect on the value of an equilibrium constant nor on equilibrium concentrations.