Unit Three
Day 32: Gibbs Free Energy and Work, Kinetic Metastability
As you work through this section, if you find that you need a bit more background material to help you understand the topics at hand, you can consult “Chemistry: The Molecular Science” (5th ed. Moore and Stanitski) Chapter 16.8 through 16.11 and Chapter 12.8, and/or Chapter 14.10-14.14 in the Additional Reading Materials section.
D32.1 Gibbs Free Energy and Work
Recall that when we we talk about kinetics of a reaction, we are concerned with the rate of the reaction: how fast it goes from reactants to products. When we talk about the thermodynamics, on the other hand, we are concerned primarily with the difference in energy between reactants and products.
When the Gibbs free energy of the products is lower than that of the reactants, a reaction is said to be exergonic, or energy releasing. The Gibbs free energy change for the reaction is negative ([latex]{\Delta}_{\text{r}}G[/latex] < 0). Conversely, an endergonic reaction is one in which the products are higher in Gibbs free energy than the reactants. An endergonic reaction has a positive [latex]{\Delta}_{\text{r}}G[/latex].
A decrease in Gibbs free energy as a reaction occurs corresponds to the maximum useful work that can be done by the reaction.
ΔrG = -wmax
Conversely, if a reaction has positive ΔrG, work must be done on the system to force the reaction to occur. The minimum work that must be done is given by ΔrG.
Exercise 1: Gibbs Free Energy and Work
Coupling of Reactions
One way to cause a reactant-favored process to occur is to couple it with a reaction that is product-favored. For example, consider the recovery of Al from Al2O3 ore:
At least 1576.4 kJ of work must be done to change 1 mol Al2O3 into 2 mol Al(s) and 1.5 mol O2(g). In a modern aluminum manufacturing plant this work is supplied electrically, and the electricity is often provided by burning coal. Assuming coal to be mainly carbon the reaction is
Thus 1 mol C can do almost exactly one-quarter the work required to decompose 1 mol Al2O3. The ΔrG° values indicate that, under standard-state conditions, at least 4 mol C must burn to process each 1 mol Al2O3 ore. (In practice the aluminum smelting process is only 17 percent efficient, so it is necessary to burn nearly 6 times the theoretical 4 mol C.) The reactions are coupled in that they occur simultaneously and there is a means of exchanging energy between them. The energy exchange occurs via the electric power grid in this specific case.
In other words, an endergonic reaction can be coupled to a separate, exergonic reaction that 'drives' the thermodynamically unfavorable one. Since Gibbs free energy is a state function, the ΔrG° values for the two coupled reactions are summed to yield the overall ΔrG°. For this example, multiply the second reaction by 4, add the reaction equations, and apply Hess's Law. The overall reaction has a negative ΔrG° and is product-favored:
D32.2 Gibbs Free Energy in Biological Systems
Biological organisms often couple the product-favored hydrolysis of ATP (adenosine triphosphate) to a reactant-favored reaction. Thus ATP hydrolysis can be used to drive otherwise reactant-favored reactions.
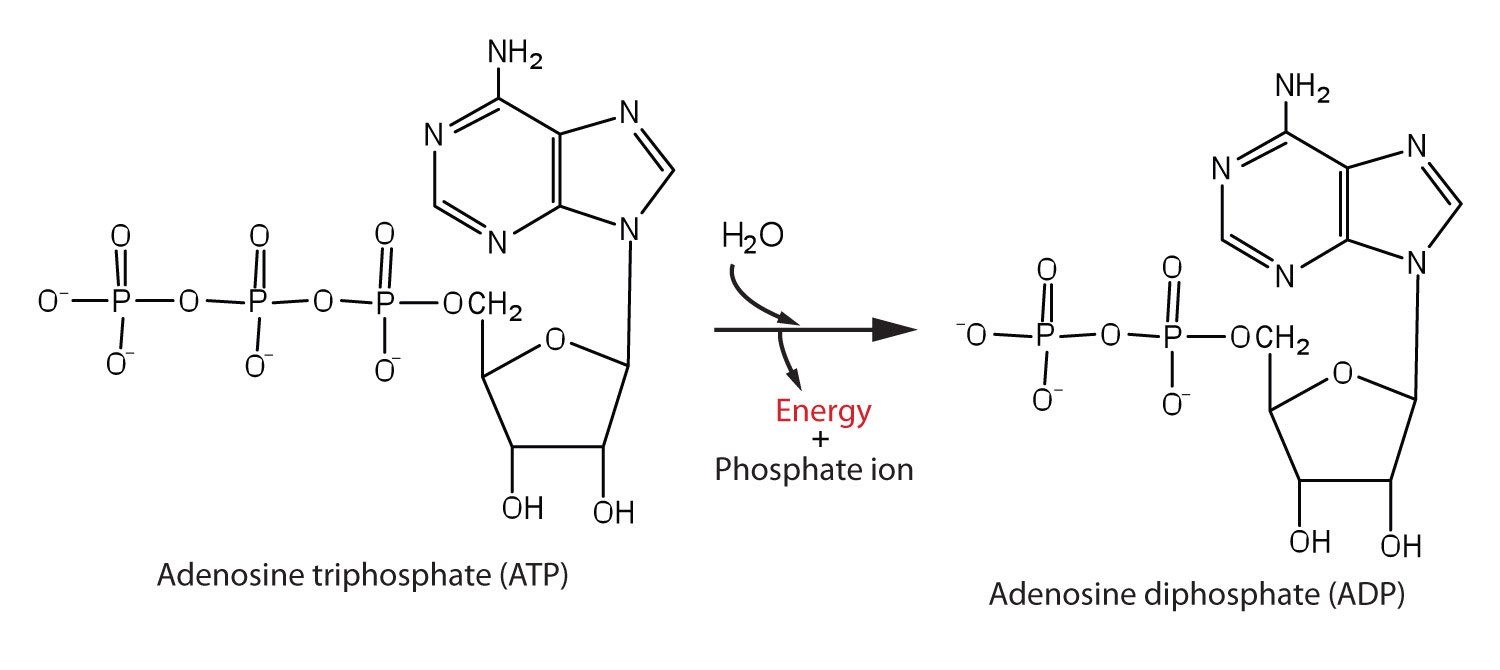
The triphosphate part of ATP is an inorganic ester; like an organic ester it can be hydrolyzed. Hydrolysis of a P–O bond in ATP to form ADP has a negative ΔrG° = −31 kJ/mol. ATP can be made available in an organism where an endergonic reaction needs to occur; ATP hydrolysis can then be coupled with the endergonic reaction to yield a thermodynamically favorable overall reaction.
For example, ATP hydrolysis can be used to combine amino acids together to generate polypeptides (and proteins) as graphically illustrated by Figure 2.
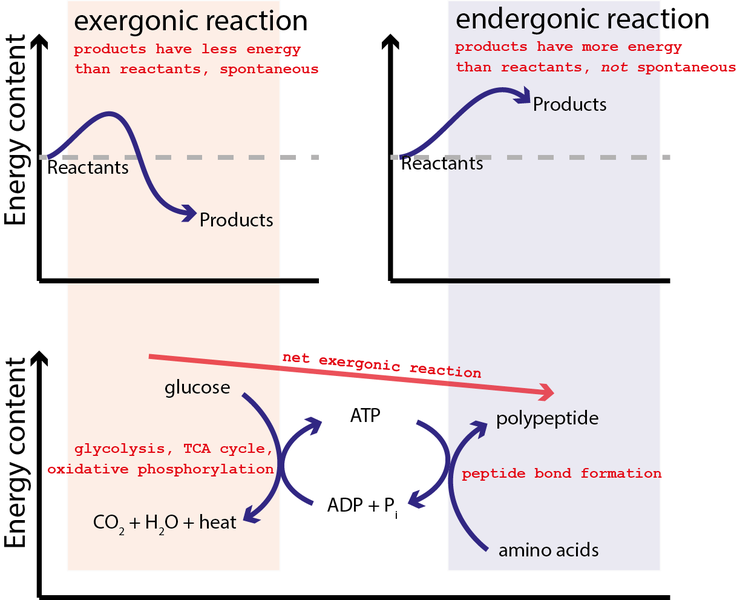
ATP formation (the reverse of ATP hydrolysis) is initially coupled to the glucose oxidization reaction:
which has ΔrG°=−2880 kJ/mol or close to 100x greater capability to do work than the hydrolysis of ATP. Hence, the equilibrium for this reaction so strongly favors the products that a single arrow is typically used in the chemical equation as it is essential irreversible. It may not be surprising that glucose and all sugars are very energetic molecules since they are the primary energy source for life.
Exercise 2: Characteristics of Exergonic Processes
D32.3 Kinetic Metastability
Both kinetics and thermodynamics are needed to fully characterize a chemical reaction. At a given temperature, the rate law and rate constant k can be used to determine how rapidly reactants are converted to products. (Rate constants can be calculated from tables of activation energies and frequency factors.) The equilibrium constant expression and the value of K° can be used to determine the equilibrium concentrations of products compared to reactants. (Equilibrium constants can be calculated from the standard reaction Gibbs free energy change ΔrG°, which in turn can be calculated from thermodynamic data tables.) The more negative ΔrG° is, the more stable products are relative to reactants.
Although kinetics describes the rates of reactions and how fast equilibrium is reached, there is not necessarily a correlation between a fast reaction and one that is product-favored. Thermodynamics tells us about conditions after equilibrium has been reached, but does not say how long it will take to achieve equilibrium. Both are important because a useful reaction usually is one where significant quantities of products can be produced in a short time. Also, it is often true that a substance is valuable for some purpose when it is stable and does not change into some other substance. For example, iron and steel are useful for making automobiles and constructing buildings precisely because they are stable.
When discussing the concept of stability, it is necessary to distinguish between thermodynamic stability and kinetic metastability.

Consider Figure 3. Here product B is at lower Gibbs free energy than reactant A so that ΔrG° of the forward reaction is negative. The reaction should therefore favor the products. We say that B is thermodynamically stable compared with A. However, if the activation-energy barrier (Ea) is high, the reaction proceeds very slowly, and reactant A would be described as being inert (unreactive). We say that A is kinetically metastable (or kinetically stable) relative to B.
For example, consider diamond and graphite, both composed only of carbon atoms. The title of an old James Bond film, and an even older advertising slogan says, "Diamonds Are Forever." This implies some stability: we don't expect the diamond in a ring to change anytime soon. Nevertheless, the most stable form of carbon at 25 °C and 1 bar is graphite. If you look up the Gibbs free energy of formation of diamond in the Appendix, ΔfG°(C(s, diamond)) = 2.9 kJ/mol. Thus, the conversion of diamond to graphite is thermodynamically favored and graphite is thermodynamically stable compared with diamond.
C(s, diamond) [latex]\longrightarrow[/latex] C(s, graphite) ΔrG° = −2.9 kJ/mol
Diamond is kinetically metastable. Thermodynamics says it should change to graphite, but the change is so slow as to be essentially undetectable in a human lifetime. The fact that diamond exists is due to a very large activation-energy barrier for conversion of diamond to graphite.
This very large activation-energy barrier, as well as the facts that diamond is the hardest known solids and graphite is one of the softest, can be explained by differences in the way the atoms are bonded. In diamond, every carbon atom has sp3 hybridization and each sp3 carbon is bonded to 4 other sp3 carbon atoms at the corners of a tetrahedron. In graphite, every carbon atom has sp2 hybridization and each sp2 carbon is bonded to 3 other sp2 carbon atoms in planar sheets of connected benzene rings. Because the sheets can slide past one another relatively easily, graphite is soft and slippery.
Conversion of diamond to graphite requires breaking a very large number of C−C single bonds with bond energy 356 kj/mol. There is no easy mechanism for this conversion and so transforming diamond into graphite, or vice versa, requires almost as much energy as destroying the entire crystal lattice and rebuilding it. Once diamond is formed, therefore, it cannot convert back to graphite because the activation-energy barrier is too high: diamond is said to be metastable, because its stability depends on kinetics, not thermodynamics.
Naturally-occurring diamonds are created deep underground under conditions of high pressure and temperature where diamond is more thermodynamically stable than graphite. Thus, over a period of millions of years carbonaceous deposits slowly crystallize into single-crystal diamond gemstones.
Exercise 3: Kinetic Metastability
What is one characteristic that is shared by many kinetically metastable substances?
D32.4 Haber-Bosch Process
The interplay of thermodynamics and kinetics is illustrated in the industrial synthesis of ammonia. It became possible to manufacture ammonia in useful quantities in the early 20th century after the factors that influence this equilibrium were understood:
Each year, ammonia is among the top 10 chemicals, by mass, manufactured in the world. It plays a vital role in the global economy. It is used in the production of fertilizers and is, itself, an important fertilizer for enhancing growth of corn, cotton, and other crops. Large quantities of ammonia are converted to nitric acid, which plays an important role in the production of fertilizers, explosives, plastics, dyes, and fibers, and is also used in the steel industry.
To be practical, an industrial process must give a large yield of product relatively quickly. One way to increase the yield of ammonia is to increase the pressure on the system, which shifts the reaction equilibrium towards the product side, increasing the concentration and partial pressure of ammonia.
At low temperatures, the rate of formation of ammonia is slow so equilibrium would be achieved more quickly at higher temperatures. However, the reaction is exothermic. Increasing the temperature to increase the rate shifts the equilibrium in the endothermic direction and lowers the product yield.
Part of the slower rate caused by operating at lower temperatures can be recovered by using a catalyst. The net effect of the catalyst on the reaction is to cause equilibrium to be reached more rapidly.
The product of the reaction, ammonia, has significantly greater intermolecular forces than do the reactants, nitrogen and hydrogen; thus, ammonia has a higher boiling point and can be condensed to a liquid at temperatures where N2 and H2 remain gases. Condensing ammonia by refrigeration of the gaseous mixture removes product, shifting the equilibrium to the right.
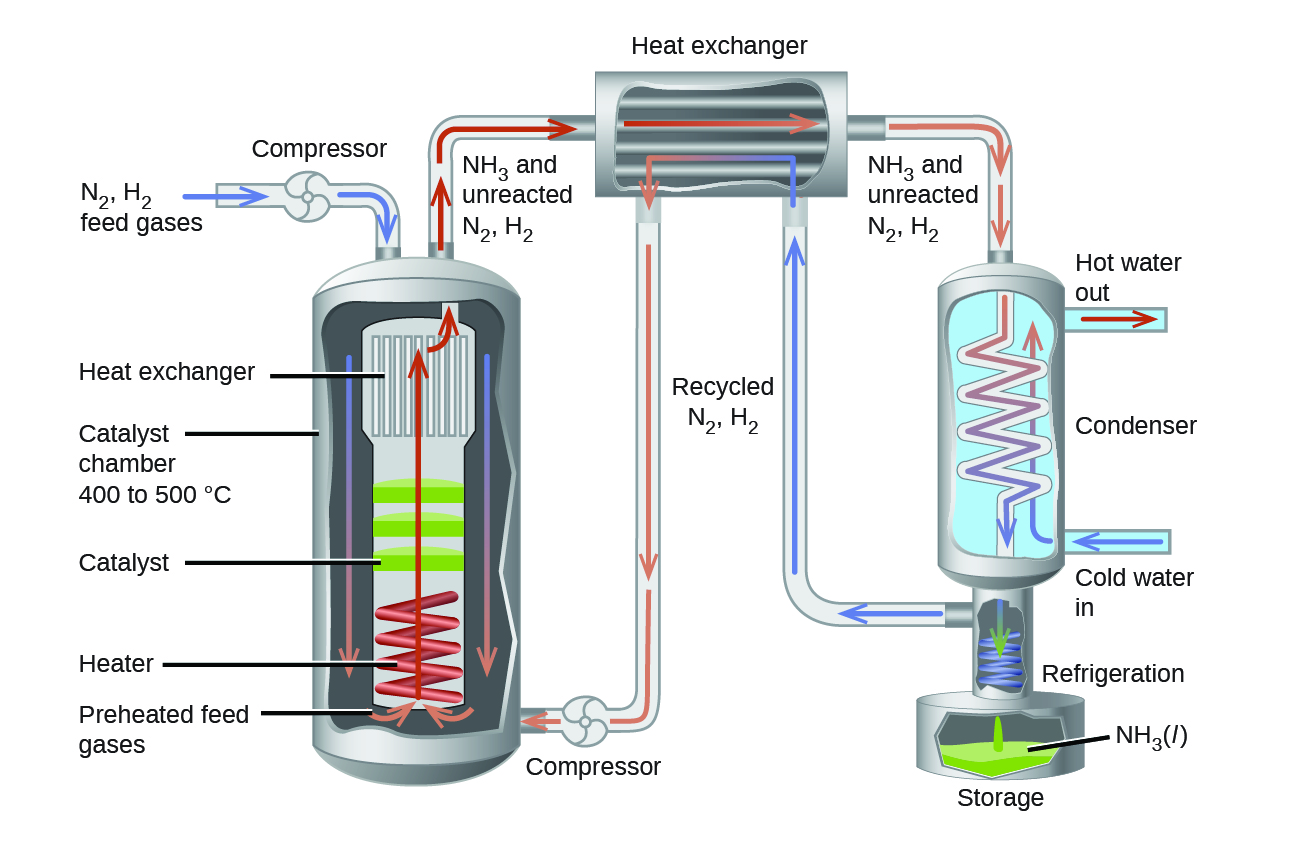
In the commercial production of ammonia, conditions of about 500 °C, 150–900 bar, and a catalyst are used to give the best compromise among rate, product yield, and the cost of the equipment necessary to produce and contain high-pressure gases at high temperatures (Figure 5).
Podia Question
Consider the addition of HBr to 1,3-butadiene. Two products are possible: 1,2-product and 1,4-product (see left side of figure).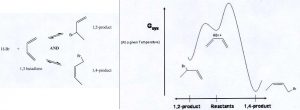
On the right side of the figure is a diagram showing Gibbs free energy as a function of reaction progress. On the horizontal axis reactants are in the middle. The 1,2-product is reached by moving left. The 1,4-product is reached by moving right.
1. Write an explanation in scientifically appropriate language for the fact that at low temperatures the reaction produces mainly 1,2-product while at high temperatures the reaction produces mainly 1,4-product. If any assumptions need to be made, say what they are.
2. A student says that at low temperatures the 1,2-product is kinetically metastable. Is this a correct statement? Why or why not?
Two days before the next whole-class session, this Podia question will become live on Podia, where you can submit your answer.

