Unit Four
Day 34: Acids and Bases
As you work through this section, if you find that you need a bit more background material to help you understand the topics at hand, you can consult “Chemistry: The Molecular Science” (5th ed. Moore and Stanitski) Chapter 3-4 and 14-1 through 14-5, and/or Chapter 15.1-15.7 in the Additional Reading Materials section.
In the last unit, we will use the knowledge we learned so far, e.g. thermodynamics, kinetics, molecular structure, etc., to explore two prevalent types of chemical reactions: acid-base reactions and redox/electrochemical reactions.
D34.1 Definition of Acids and Bases
Around 1815, Humphry Davy demonstrated that hydrogen is the essential constituent of acids, and Joseph Louis Gay-Lussac concluded that acids are substances that can neutralize bases and these two classes of substances can be defined only in terms of each other. The significance of hydrogen was reemphasized in 1884 when Svante Arrhenius defined an acid as a compound that dissolves in water to yield hydrogen cations (or protons, H+) and a base as a compound that dissolves in water to yield hydroxide anions (OH−). This Arrhenius acid-base definition is useful in some contexts but limited in scope.
A more general definition, centered on the proton, was proposed in 1923 by the Danish chemist Johannes Brønsted and the English chemist Thomas Lowry: According to the Brønsted-Lowry acid-base definition, a chemical species (ion or molecule) that donates a proton to another chemical species is called an acid and a chemical species that accepts a proton is a base. An acid-base reaction is the transfer of a proton from a proton donor (acid) to a proton acceptor (base).
Although we will not discuss it much in this course, there is an even more general model of acid-base behavior introduced by the American chemist G. N. Lewis. The Lewis acid-base definition says that an acid is a chemical species that can accept a pair of electrons and form a bond; a base is a chemical species that can donate a pair of electrons.
Here we will use the Brønsted-Lowry definition. The chemical species that remains after an acid has donated a proton is called the conjugate base of that acid. Consider the following examples of the generic reaction acid + H2O ⇌ conjugate base + H3O+:
H2SO4 + H2O ⇌ HSO4- + H3O+
H2O + H2O ⇌ OH- + H3O+
HSO4- + H2O ⇌ SO42- + H3O+
NH4+ + H2O ⇌ NH3 + H3O+
(Note that in each of these reactions there is a second acid-base pair: H2O is the conjugate base of the acid H3O+.)
Similarly, the chemical species that forms after a base accepts a proton is called the conjugate acid of that base. Consider the following examples of the generic reaction base + H2O ⇌ conjugate acid + OH-:
H2O + H2O ⇌ H3O+ + OH-
NH3 + H2O ⇌ NH4+ + OH-
S2- + H2O ⇌ HS- + OH-
CO32- + H2O ⇌ HCO3- + OH-
F- + H2O ⇌ HF + OH-
(Note that in these reactions there is also a second acid-base pair: H2O is the conjugate acid of the base OH-)
According to the Brønsted-Lowry definition, all acid-base reactions involve the transfer of a protons between an acid and a base. For example, consider the acid-base reaction that takes place when ammonia is dissolved in (and reacts with) water. A water molecule (functioning as an acid here) transfers a proton to an ammonia molecule, yielding the conjugate base of water, OH−, and the conjugate acid of ammonia, NH4+:
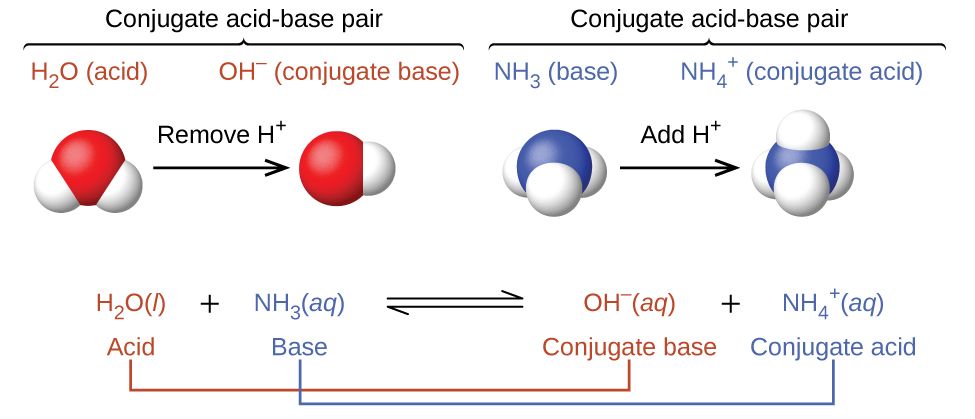
Note that acid-base reactions are often represented as equilibrium processes. The relative extent to which these reactions proceed is an important aspect when we consider acid and base strengths later.
Exercise 1: Brønsted-Lowry Acids and Bases
Identify whether each molecule is a Brønsted-Lowry acid or a base (relative to water), and write the formula for its conjugate partner (i.e. if it’s an acid, write its conjugate base, if it’s a base, write its conjugate acid).
[Enter the formula for each without subscripts and superscripts, and put any charge in parentheses. For example, enter HSO4– as HSO4(-)]
D34.2 Autoionization of Water
In previous discussion, it was clear that water can function as an acid or a base depending on the nature of the solute dissolved in it. In pure water, water acts both as an acid and a base—a very small fraction of water molecules donate protons to other water molecules:
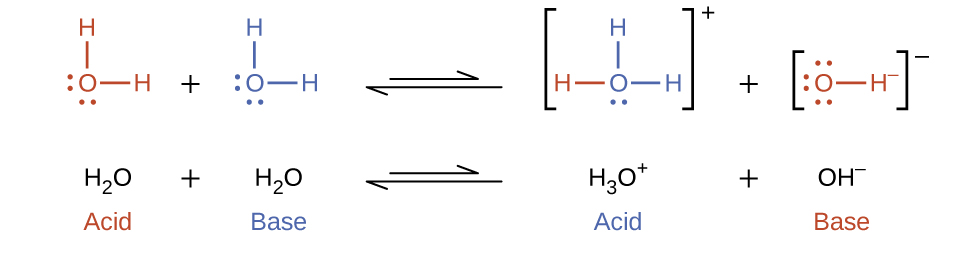
This type of reaction, in which a substance ionizes when one molecule of the substance reacts with another molecule of the same substance, is referred to as autoionization.
Pure water undergoes autoionization to a very slight extent: only about two out of every 109 molecules are ionized at 25 °C. The very small concentrations of H3O+ and H3O+ give an autoionization constant for water, Kw = 1.0 × 10−14 M2 at 25 °C. Because it is the mathmatical product of concentrations of two ions, it is also called the ion-product constant for water.
The process is endothermic, and so the extent of ionization increases with temperature. For example, at 100 °C, Kw is about 5.6 × 10−13 M2, roughly 50 times larger than the value at 25 °C.
Example 1
Ion Concentrations in Pure Water
What are the H3O+ concentration and the OH- concentration in pure water at 25 °C?
Solution
The autoionization of water yields the same number of hydronium and hydroxide ions. Therefore, in pure water, [H3O+] = [OH−]. At 25 °C,
so
The hydronium ion concentration and the hydroxide ion concentration are the same, and we find that both equal 1.0 × 10−7 M at 25 °C.
Check Your Learning
At 80 °C, Kw = 2.4 × 10−13 M2. Determine the concentrations of hydronium and hydroxide ions in pure water at 80 °C.
Answer:
[H3O+] = [OH−] = 4.9 × 10−7M
Example 2
The Inverse Proportionality of [H3O+] and [OH−]
A solution of carbon dioxide in water has [H3O+] = 2.0 × 10−6 M. Calculate the concentration of OH- at 25 °C.
Solution
The ion-product constant for water at 25 °C is
Thus, we can calculate the missing equilibrium concentration.
Rearrangement of the Kw expression yields:
The hydroxide ion concentration is reduced to 5.0 × 10−9 M as the hydronium ion concentration increases to 2.0 × 10−6 M. This is expected from Le Châtelier’s principle: the autoionization reaction shifts to the left to partly counteract the increased hydronium ion concentration and the [OH−] is reduced relative to that in pure water.
A check of these concentrations confirms that our arithmetic is correct:
Check Your Learning
Calculate the hydronium ion concentration in an aqueous solution with a hydroxide ion concentration of 0.001 M at 25 °C.
Answer:
[H3O+] = 1 × 10−11 M
Water is an example of a molecule or ion that can gain or lose a proton in acid-base reactions, an amphiprotic chemical species. Amphiprotic species are also amphoteric, a more general term for a species that may act either as an acid or a base by any definition (not just the Brønsted-Lowry definition). Consider for example the bicarbonate ion:
HCO3-(aq) + H2O(l) ⇌ H2CO3(aq) + OH-(aq)
Example 3
Representing the Acid-Base Behavior of an Amphiprotic Species
Write separate equations representing the reaction of HSO3-
(a) as an acid with OH−
(b) as a base with HI
Solution
(a) [latex]\text{HSO}_3^-(\text{aq})\;+\;\text{OH}^{-}(\text{aq})\;{\rightleftharpoons}\;\text{SO}_3^{2-}(\text{aq})\;+\;\text{H}_2\text{O}(l)[/latex]
(b) [latex]\text{HSO}_3^{-}(\text{aq})\;+\;\text{HI}(\text{aq})\;{\rightleftharpoons}\;\text{H}_2\text{SO}_3(\text{aq})\;+\;\text{I}^{-}(\text{aq})[/latex]
Check Your Learning
Write separate equations representing the reaction of H2PO4-
(a) as a base with HBr
(b) as an acid with OH−
Answer:
(a) [latex]\text{H}_2\text{PO}_4^{-}(\text{aq})\;+\;\text{HBr}(\text{aq})\;{\rightleftharpoons}\;\text{H}_3\text{PO}_4(\text{aq})\;+\;\text{Br}^{-}(\text{aq})[/latex];
(b) [latex]\text{H}_2\text{PO}_4^{-}(\text{aq})\;+\;\text{OH}^{-}(\text{aq})\;{\rightleftharpoons}\;\text{HPO}_4^{2-}(\text{aq})\;+\;\text{H}_2\text{O}(l)[/latex]
D34.3 pH and pOH
The concentrations of hydronium cations and hydroxide anions in a solution are important for the solution's acid-base properties and often affect the chemical behaviors of its other solutes. A solution is neutral if it contains equal concentrations of hydronium and hydroxide ions; acidic if [H3O+] > [OH-]; and basic if [H3O+] < [OH-].
A common means of expressing values that may span many orders of magnitude is to use a logarithmic scale. One such scale is based on the p-function:
where “X” is the quantity of interest and “log” is the base-10 logarithm. The pH of a solution is therefore defined as:
The reason for dividing by the units mol/L is that [H3O+] has units mol/L and taking the logarithm of a unit makes no sense. From here on we will assume that you are aware that only the numeric value of a concentration (or other quantity) needs to be used as the argument of a logarithm and we will not explicitly divide by the units.
If a pH value is known, the concentration of hydronium ions can be calculated
Here we assume that you know that units are required for the concentration obtained from this equation and the units are mol/L. Similarly, the hydroxide ion concentration may be expressed as pOH:
Finally, the relation between pH and pOH can be derived from the Kw expression:
-log(Kw) = -log([H3O+][OH-]) = -log([H3O+]) + (-log([OH-]))
pKw = pH + pOH
At 25 °C:
Therefore, at this temperature:
| Classification | Relative Ion Concentrations | pH at 25 °C |
|---|---|---|
| acidic | [H3O+] > [OH−] | pH < 7 |
| neutral | [H3O+] = [OH−] | pH = 7 |
| basic | [H3O+] < [OH−] | pH > 7 |
Because Kw is temperature dependent, these correlations between pH values and the acidic/neutral/basic adjectives are different at different temperatures. For example, [H3O+] in pure water at 80 °C is 4.9 × 10−7 M, which corresponds to pH and pOH values of:
pOH = -log[OH-] = -log(4.9 × 10−7) = 6.31
At this temperature, then, neutral solutions exhibit pH = pOH = 6.31, acidic solutions exhibit pH < 6.31 and pOH > 6.31, whereas basic solutions exhibit pH > 6.31 and pOH < 6.31. This distinction can be important when studying certain processes that occur at temperatures other than 25 °C.
Unless otherwise noted, references to pH values are presumed to be those at 25 °C. Figure 1 shows the relationships between [H3O+], [OH−], pH, and pOH, and gives values for these properties for some common substances.
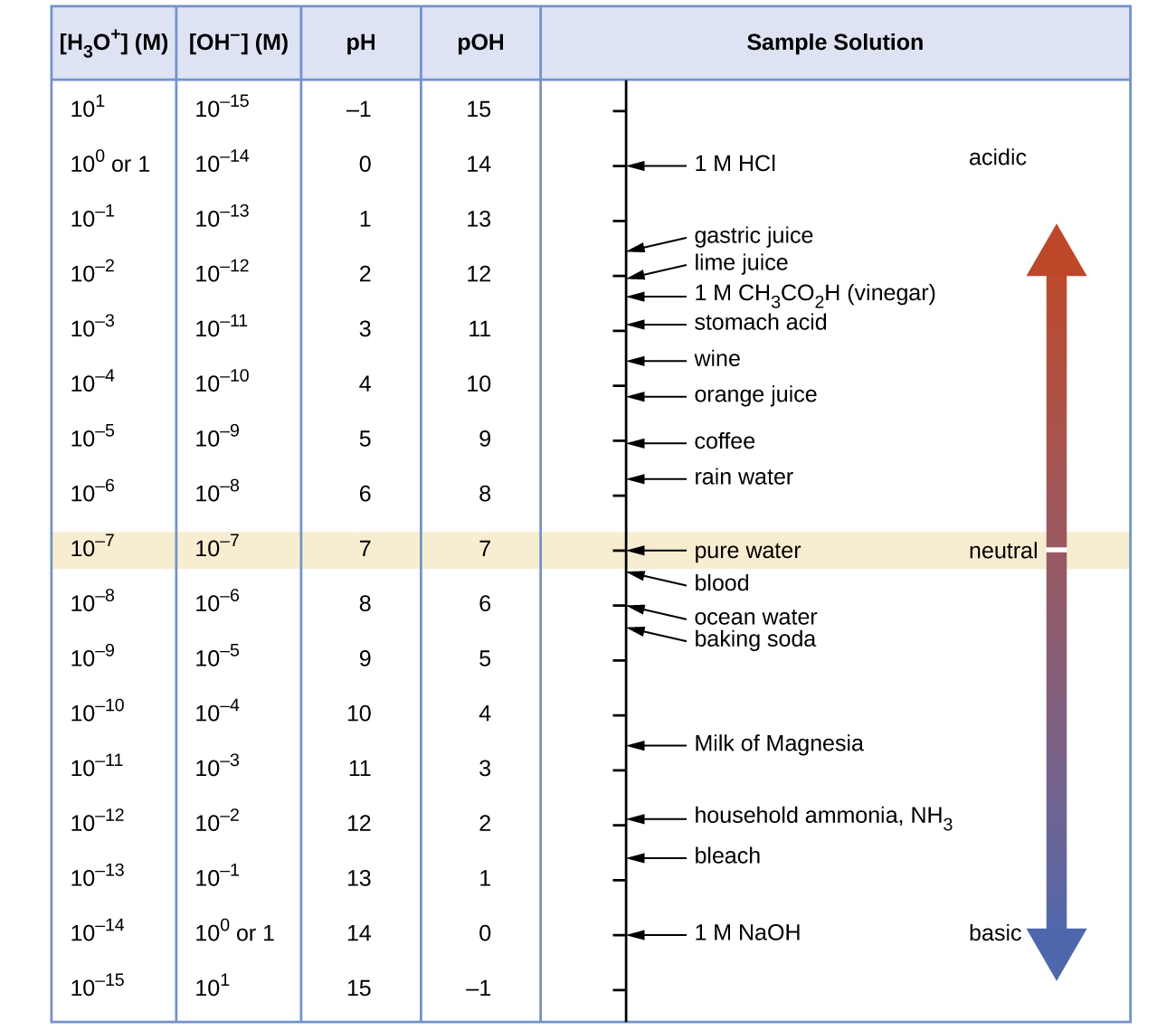
Exercise 2: pH and Relative Strengths of Acids
Experiments show that the pH of a 0.010 M HCN aqueous solution is higher than the pH of a 0.010 M CH3COOH aqueous solution. Based on this observation, what can you deduce about the relative acidity of HCN (prussic acid) and CH3COOH (acetic acid)? Explain your answer.
Example 4
Calculation of pH from [H3O+]
What is the pH of stomach acid, a solution of HCl with a hydronium ion concentration of 1.2 × 10−3M?
Solution
(When taking the log of a value, keep as many decimal places in the result as there are significant figures in the value.)
Check Your Learning
Water exposed to air contains carbonic acid, H2CO3, due to the reaction between carbon dioxide and water:
Air-saturated water has a hydronium ion concentration caused by the dissolved CO2 of 2.0 × 10−6 M, about 20-times larger than that of pure water. Calculate the pH of the solution at 25 °C.
Answer:
5.70
Example 5
Calculation of Hydronium Ion Concentration from pH
Calculate the hydronium ion concentration of blood, the pH of which is 7.3 (slightly alkaline).
Solution
(On a calculator take the antilog, or the “inverse” log, of −7.3, or calculate 10−7.3.)
Check Your Learning
Calculate the hydronium ion concentration of a solution with a pH of −1.07.
Answer:
12 M
The acidity of a solution is typically determined by measuring its pH. The pOH of a solution is not usually measured, but it is easily calculated from an experimentally determined pH value. The pH of a solution can be directly measured using a pH meter (Figure 2), or visually estimated using colored indicators (Figure 3).


D34.4 Acid Constant Ka and Base Constant Kb
The relative strengths of acids and bases may be determined by comparing the equilibrium constants for their ionization reactions. For the reaction of a generic acid, HA, in water:
we write the acid ionization constant (Ka) expression as:
(Although water is a reactant in the reaction, it is the solvent as well, so we do not include [H2O] in the expression.) The larger the Ka of an acid, the larger the concentration of H3O+ and A− relative to the concentration of the nonionized acid, HA. Thus a stronger acid, which ionizes to a greater extent, has a larger ionization constant than a weaker acid.
For example, the following data on acid ionization constants indicate the order of acid strength CH3COOH < HNO2 < HSO4-:
HNO2(aq) + H2O(l) ⇌ O2-(aq) + H3O+(aq) Ka = 7.4 × 10-4
HSO4-(aq) + H2O(l) ⇌ SO42-(aq) + H3O+(aq) Ka = 1.1 × 10-2
We can consider the strength of a base (B) similarly by its tendency to form hydroxide ions in aqueous solution:
where the base ionization constant (Kb) expression is:
In solutions of the same concentration, stronger bases ionize to a greater extent, and so yield higher hydroxide ion and HB+ concentrations than do weaker bases. Therefore, a stronger base has a larger Kb than a weaker base.
Notice that Ka and Kb provide a quantitative measure of acid and base strengths—significantly more accurate than just saying "strong acid" or "weak acid". For example, some weak acids are stronger than other weak acids, as indicated by their larger Ka values.
Optional: try this simulation of strong and weak acids and bases at the molecular level.
Consider the ionization reactions for a conjugate acid base pair, HA and A−:
A-(aq) + H2O(l) ⇌ HA(aq) + OH-(aq) [latex]K_{\text{b}} = \dfrac{[\text{HA}][\text{OH}^{-}]}{[\text{A}^{-}]}[/latex]
Adding these two chemical equations yields the equation for the autoionization of water:
When two equilibria sum to a third equilibrium, the product of the first two equilibrium constants equals the third equilibrium constant, so
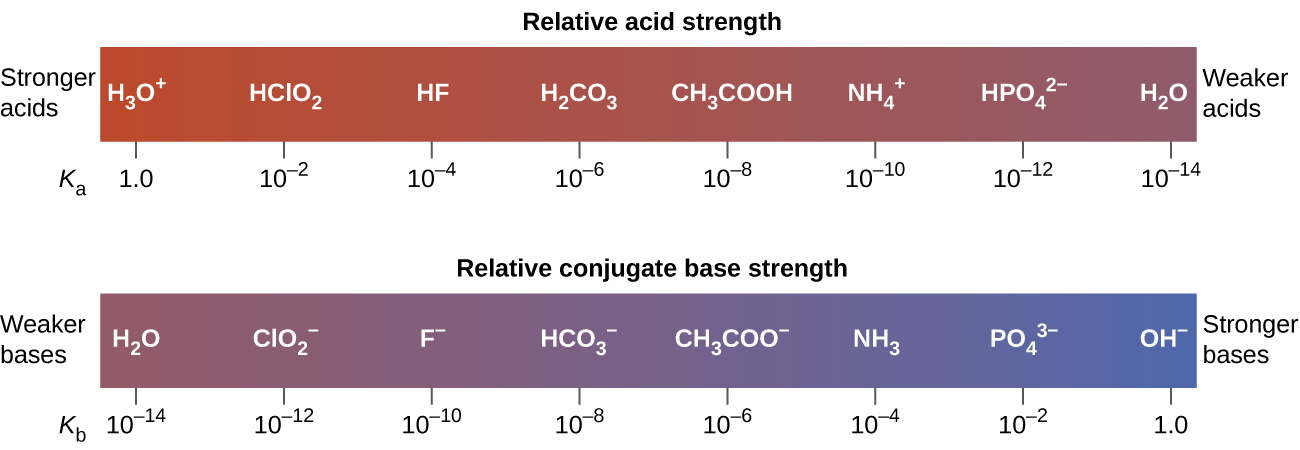
For example, at 25 °C, Ka of acetic acid (CH3COOH) is 1.8 × 10−5 M, and Kb of its conjugate base, acetate ion (CH3COO-), is 5.6 × 10−10 M. The product of these two constants is indeed equal to Kw:
This relationship tells us that stronger acids form weaker conjugate bases, and weaker acids form stronger conjugate bases (Figure 4 and Figure 5).
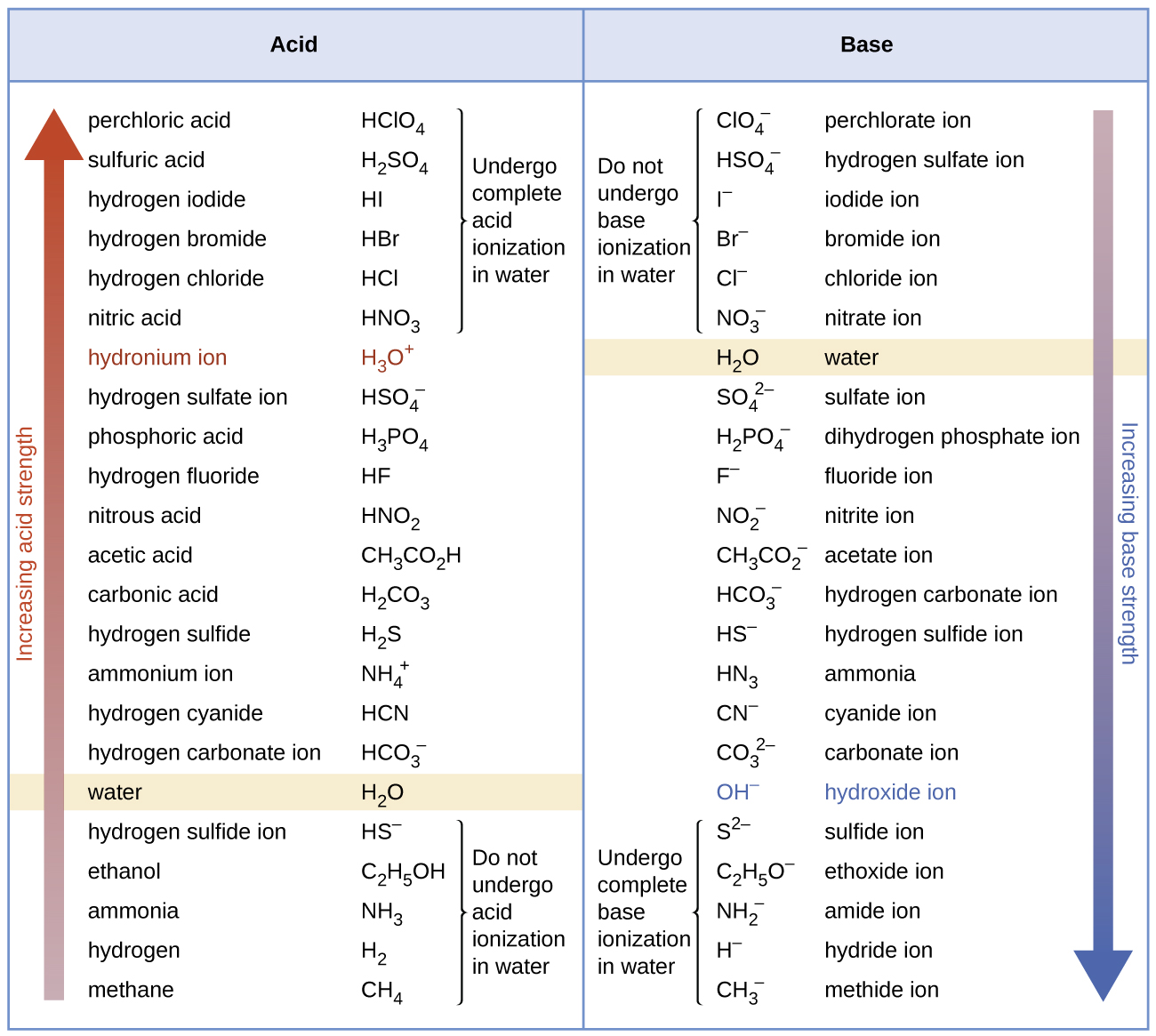
Although "strong" and "weak" are relative terms, in aqueous solutions acids stronger than H3O+ are called strong acids, and bases stronger than OH- are strong bases. Because strong acids and strong bases are completely ionized in aqueous solutions, the concentration of nonionized acid or base is essentially zero. For example, in a 0.10-M solution of HCl, [HCl] = 0, [H30+] = 0.10 M, and [Cl−] = 0.10 M. A consequence of this complete ionization is that in aqueous solution there is no way to tell whether one strong acid is stronger than another: HCl, HBr, and HI all are completely ionized. This is known as the leveling effect of water. However, when dissolved in ethanol (a weaker base than water), these acids do not ionize completely. The extent of ionization increases in the order HCl < HBr < HI, and so HI is the strongest of these acids. Water exerts a similar leveling effect on strong bases.
Many acids and bases are weak. A solution of a weak acid in water is a equilibrium mixture of the nonionized acid, hydronium ion, and the conjugate base of the acid, with the nonionized acid present in the greatest concentration. Most aqueous acid-base reactions reach equilibrium in less than a millisecond—the reactions are rapid.
Example 6
Determination of Ka or Kb from pH
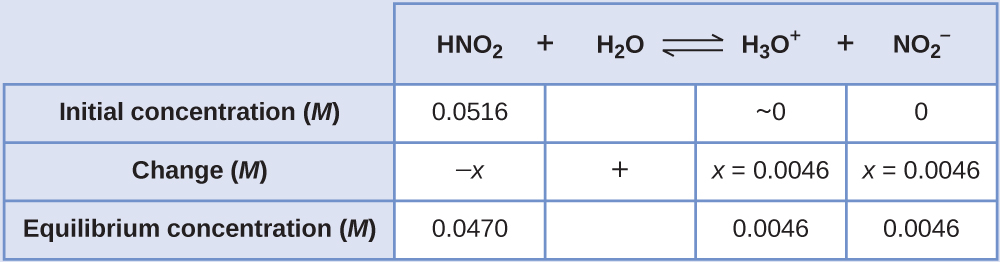
One way to determine Ka or Kb is to determine [H3O+] by measuring pH for a solution of known initial concentration of acid. For example, calculate Ka for nitrous acid if the pH of a 0.0516-M solution of HNO2 is is measured as 2.34.
Solution
An ICE table is useful in solving this type of problem. Initially, before the rapid acid-base reaction occurs, the concentrations are HNO2, 0.0516 M; H3O+, 1.0 × 10−7 M; and NO2-, 0.0 M so the first row of the ICE table can be filled in.
The equilibrium concentration of hydronium ion can be obtained from the pH:
Let x be the change in [H3O+], that is the difference between the equilibrium concentration of H3O+, 0.0046 M, and the initial concentration, 1.0 × 10−7 M. Thus x = (0.0046 − 1.0 × 10−7) M = 0.0045999 M, which rounds to 0.0046 M to two significant figures. Note that the initial concentration of H3O+ is so small that it is negligible; this is often true, but needs to be checked.
The change in concentration of NO2- equals the change in concentration of H3O+. The equilibrium concentration of HNO2 is equal to its initial concentration plus the change in its concentration, −x.
Now complete the ICE table with equilibrium concentrations and calculate Ka:
Check Your Learning.
Determine Kb for NH3, given that the pH of a 0.950-M solution of NH3, is 11.612.
Answer:
Kb = 1.77 × 10−5 M (There are 3 sig figs in the answer because there are three digits to the right of the decimal point in the pH; digits to the left of the decimal point are the power of 10 and are not significant.)
Given the initial concentration of a weak acid or base, Ka or Kb can be used to calculate the concentrations of ions in solution.
Example 7
Equilibrium Concentrations in a Solution of a Weak Acid
Formic acid, HCO2H, is the irritant that causes the body’s reaction to ant bites. Calculate the concentration of hydronium ion and the pH in a 0.534-M solution of formic acid.
Solution
- Determine x and equilibrium concentrations. The table shows initial concentrations (concentrations before the acid ionizes), changes in concentration, and equilibrium concentrations (the data given in the problem appear in color):
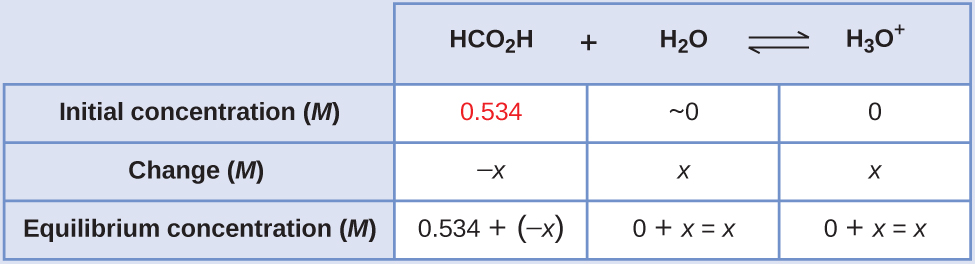
- Solve for x and the equilibrium concentrations.
At equilibrium:
solving this quadratic equation gives:
We find the equilibrium concentration of hydronium ion in this formic acid solution from its initial concentration and the change in that concentration:
The pH of the solution can be found by taking the negative log of the [H3O+]:
Check Your Learning
Find the concentration of hydroxide ion in a 0.0325-M solution of ammonia, a weak base with a Kb of 1.76 × 10−5 M.
Answer:
7.56 × 10−4 M
D34.5 Percent Ionization
The percent ionization of a weak acid is another measure of the strength of an acid, HA:
Stronger acids, with higher Ka, therefore have higher percent ionization (for a given concentration). The percent ionization for a solution of a given weak acid increases with decreasing acid concentration; this can be seen by applying Le Chatelier's principle to the ionization equilibrium:
HA(aq) + H2O(l) ⇌ A-(aq) + H3O+(aq)
Increasing the solution volume for a given quantity of HA added causes the equilibrium to shift to the product side to partially counteract the decrease in total solute concentration.
Example 8
Calculation of Percent Ionization from pH
Calculate the percent ionization of a 0.125-M solution of nitrous acid (a weak acid), with a pH of 2.09.
Solution
The percent ionization for an acid is:
The chemical equation for the dissociation of the nitrous acid is:
Since
we find that 10−2.09 = 8.1 × 10−3, and
(The logarithm 2.09 indicates a hydronium ion concentration with only two significant figures.)
Check Your Learning
Calculate the percent ionization of a 0.10-M solution of acetic acid with a pH of 2.89.
Answer:
1.3% ionized
D34.6 Acid Strength and Molecular Structure
Acid-base reactions, like many other chemical reactions, involve breaking and forming bonds. Hence, we can use our chemical understanding of molecular structure and stability to understand what makes some acids stronger than others.
Let's consider a generic acid:
In general, the stronger the H–A bond, the less likely the bond is to break to form H+ ions and thus the less acidic the substance. This effect is illustrated by the hydrogen halides:
| Relative Acid Strength | HF | HCl | HBr | HI |
|---|---|---|---|---|
| H–X Bond Energy (kJ/mol) | 566 | 431 | 366 | 299 |
| pKa | 3.2 | −6.1 | −8.9 | −9.3 |
As you go down the halide group, the overlap between the 1s orbital of hydrogen and the valence orbital of the halogen atom decreases, and the H-X bond becomes weaker. As a result, HX acid strength increases. A similar trend is observed for other groups. For example, for group 16 (with pKa values in parentheses):
We know that an equilibrium favors the thermodynamically more stable side, and that the magnitude of the equilibrium constant reflects the energy difference between the components of each side. Therefore, in an acid-base equilibrium, the equilibrium will always favors the side with weaker acid and base (these are the more stable species). Consequently, anything that stabilizes the conjugate base of an acid will necessarily make that acid stronger.
For instance, factors that stabilize the excess negative charge on the conjugate base (A-) would favor the dissociation of H+ and make the parent acid (HA) stronger. For example, the relative acidity of the acids with second row elements is (with pKa values in parentheses):
Consider the compounds at both ends of this series: methane and hydrogen fluoride. The conjugate base of CH4 is CH3-, and the conjugate base of HF is F−. Because fluorine is much more electronegative than carbon, fluorine can better stabilize the negative charge in the F− ion than carbon can stabilize the negative charge in the CH3− ion. Consequently, HF has a greater tendency to dissociate to form H+ and F− than does methane to form H+ and CH3-, making HF a much stronger acid than CH4.
The same trend is predicted by analyzing the acids: as the electronegativity of A in HA increases, the A–H bond becomes more polar, favoring dissociation to form A− and H+. Due to both the increasing stability of the conjugate base and the increasing polarization of the A–H bond in the acid, acid strengths of binary hydrides increase as we go from left to right across a row of the periodic table.
The stability of conjugate base also affects acidities of carboxylic acids. The pKa values of some typical carboxylic acids are listed in the table. When we compare these values with those of comparable alcohols, such as ethanol (pKa = 16) and 2-methyl-2-propanol (pKa = 19), it is clear that carboxylic acids are stronger acids by over ten orders of magnitude.
| Compound | pKa | Compound | pKa | |
|---|---|---|---|---|
| HCOOH | 3.75 | CH3CH2CH2COOH | 4.82 | |
| CH3COOH | 4.74 | ClCH2CH2CH2COOH | 4.53 | |
| FCH2COOH | 2.65 | CH3CHClCH2COOH | 4.05 | |
| ClCH2COOH | 2.85 | CH3CH2CHClCOOH | 2.89 | |
| BrCH2COOH | 2.90 | C6H5COOH | 4.20 | |
| ICH2COOH | 3.10 | p-O2NC6H4COOH | 3.45 | |
| Cl3CCOOH | 0.77 | p-CH3OC6H4COOH | 4.45 |
Why should the presence of a carbonyl group adjacent to a hydroxyl group have such a profound effect on the acidity of the hydroxyl proton? Both the carboxyl group and the carboxylate anion are stabilized by resonance, but the stabilization of the anion is much greater. In the carboxylate anion, the two contributing structures have equal weight, and the C–O bonds are of equal length (between a double and a single bond). This stabilization leads to a markedly increased acidity.

Atoms (or groups of atoms) in a molecule that are not directly bonded to the acidic H can also influence the molecule's acidity. They can do so via an inductive effect, that is, they induce a change in the distribution of electrons within the molecule. This can be seen in the table above where electronegative substituents near the carboxyl group act to increase the acidity. For example, fluoroacetic acid, FCH2COOH, is significantly more acidic (lower pKa) than acetic acid, CH3COOH. The magnitude of the inductive effect depends on both the nature and the number of halogen substituents, as shown by the pKa values for several acetic acid derivatives:
Fluorine, which is more electronegative than chlorine, causes a larger effect, and the effect of three halogens is greater than the effect of two or one. Notice from these data that inductive effects can be quite significant. For instance, replacing the –CH3 group of acetic acid by a –CF3 group results in about a 10,000-fold increase in acidity.
In another example, the acidity of hypohalous acids (HOX(aq) ⇌ H+(aq) + OX−(aq)) varies by about three orders of magnitude due to the difference in electronegativity of the halogen atoms:
| HOX | Electronegativity of X | pKa |
|---|---|---|
| HOCl | 2.73 | 7.2 |
| HOBr | 2.64 | 8.5 |
| HOI | 2.11 | 10.5 |
As the electronegativity of X increases, the electrons are drawn more strongly toward the halogen atom and, in turn, away from the H in the O–H bond, thus weakening the O–H bond and allowing dissociation of hydrogen as H+.
The acidity of oxoacids, with the general formula HOXOn (with n = 0−3), depends strongly on the number of terminal oxygen atoms attached to the central atom X (Figure 6) due to both an inductive effect and increased stabilization of the conjugate base.
Because oxygen is the second most electronegative element, adding terminal oxygen atoms causes electrons to be drawn away from the O–H bond, making it weaker and thereby increasing the strength of the acid. Figure 6 shows how the H atom becomes steadily more blue from HClO to HClO4, making it easier to lose hydrogen as H+ ion.

Also important is the effect of delocalization of the negative charge in the conjugate base. As shown in Figure 7, the number of important resonance structures for the oxoanions of chlorine increases as the number of terminal oxygen atoms increases, indicating that the excess electron is delocalized over successively more oxygen atoms, stabilizing the conjugate base.
For example, in the perchlorate ion (ClO4-), the single negative charge is delocalized over all four oxygen atoms, whereas in the hypochlorite ion (ClO−), the negative charge is largely localized on a single oxygen atom. As a result, the perchlorate ion has no localized negative charge to which a proton can bind. Consequently, the perchlorate anion has a much lower affinity for a proton than does the hypochlorite ion, and perchloric acid is one of the strongest acids known.

The inductive effect is additionally responsible for the trend in the acidities of oxoacids that have the same number of oxygen atoms as we go across a row of the periodic table. For example, H3PO4 is a weak acid, H2SO4 is a strong acid, and HClO4 is one of the strongest acids known. The number of terminal oxygen atoms increases steadily across the row, consistent with the observed increase in acidity. In addition, the electronegativity of the central atom increases steadily from P to S to Cl, which causes electrons to be drawn from oxygen to the central atom, weakening the O–H bond and increasing the strength of the oxoacid.
Podia Question
Sodium hydrogen sulfate, NaHSO4, is used in some household cleansers because it contains HSO4-, a weak acid. Calculate the pH of a 0.50-M solution of NaHSO4.
Two days before the next whole-class session, this Podia question will become live on Podia, where you can submit your answer.

