Unit Four

Day 36: Buffer Solutions

As you work through this section, if you find that you need a bit more background material to help you understand the topics at hand, you can consult “Chemistry: The Molecular Science” (5th ed. Moore and Stanitski) Chapter 15-1, and/or Chapter 15.15-15.16 and Chapter 16.1-16.4 in the Additional Reading Materials section.

D36.1 Buffer Solutions

A mixture of a weak acid and its conjugate base, such as acetic acid and sodium acetate (CH3COOH + CH3COONa), or a mixture of a weak base and its conjugate acid, such as ammonia and ammonium chloride (NH3 + NH4Cl), is a buffer solution. A buffer solution resists changes in pH when small amounts of a strong acid or a strong base are added (Figure 1).

Two images are shown. Image a on the left shows two beakers that each contain yellow solutions. The beaker on the left is labeled “Unbuffered” and the beaker on the right is labeled “p H equals 8.0 buffer.” Image b similarly shows 2 beakers. The beaker on the left contains a bright orange solution and is labeled “Unbuffered.” The beaker on the right is labeled “p H equals 8.0 buffer.”
Figure 1. (a) The buffered solution on the left and the unbuffered solution on the right have the same pH (pH 8), showing the yellow color of the indicator methyl orange. (b) After the addition of 1 mL of a 0.01-M HCl solution, the buffered solution pH has not changed detectably. The unbuffered solution has become acidic, as indicated by the red color of the methyl orange, which turns red at a pH of about 4. (credit: modification of work by Mark Ott)

A solution containing equal concentrations of CH3COOH and CH3COONa is slightly acidic because the Ka of acetic acid is greater than the Kb of its conjugate base acetate ion. When a strong base, such as NaOH, is added, the OH– ions react with the few H3O+ ions, decreasing [H3O+]. This shifts the equilibrium of acetic acid reacting with water to the right, restoring [H3O+] to almost its original value:

CH3COOH(aq) + H2O(l) → CH3COO–(aq) + H3O+(aq)

In effect, most of the added NaOH reacts with the weak acid, CH3COOH, converting it to a weak base, CH3COO−. There is only a small decrease in [H3O+].

CH3COOH(aq) + OH–(aq) → CH3COO–(aq) + H2O(l)

When a strong acid, such as HCl, is added, most of the added H3O+ ions react with acetate ions, forming acetic acid molecules. There is only a small increase in [H3O+].

CH3COO–(aq) + H3O+(aq) → CH3COOH(aq) + H2O(l)

Thus, in both situations, the pH remains essentially unchanged (Figure 2).

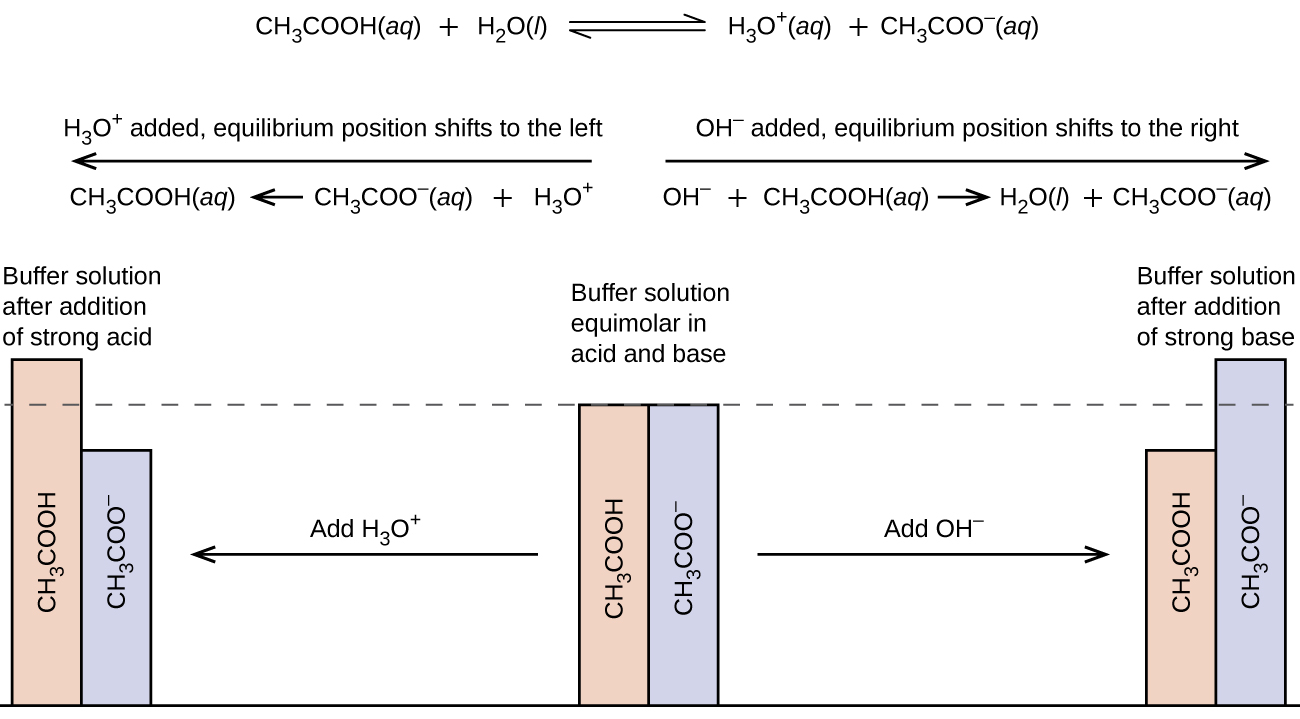
This figure begins with a chemical reaction at the top: C H subscript 3 C O O H ( a q ) plus H subscript 2 O ( l ) equilibrium arrow H subscript 3 O superscript positive sign ( a q ) plus C H subscript 3 C O O superscript negative sign ( a q ). Below this equation are two arrows: one pointing left and other pointing right. The arrow pointing left has this phrase written above it, “H subscript 3 O superscript positive sign added, equilibrium position shifts to the left.” Below the arrow is the reaction: C H subscript 3 C O O H ( a q ) left-facing arrow C H subscript 3 C O O superscript negative sign ( a q ) plus H subscript 3 O superscript positive sign. The arrow pointing right has this phrase written above it, “O H subscript negative sign added, equilibrium position shifts to the right.” Below the arrow is the reaction: O H superscript negative sign plus C H subscript 3 C O O H ( a q ) right-facing arrow H subscript 2 O ( l ) plus C H subscript 3 C O O superscript negative sign ( a q ). Below all the text is a figure that resembles a bar graph. In the middle are two bars of equal height. One is labeled, “C H subscript 3 C O O H,” and the other is labeled, “C H subscript 3 C O O superscript negative sign.” There is a dotted line at the same height of the bars which extends to the left and right. Above these two bars is the phrase, “Buffer solution equimolar in acid and base.” There is an arrow pointing to the right which is labeled, “Add O H superscript negative sign.” The arrow points to two bars again, but this time the C H subscript 3 C O O H bar is shorter than that C H subscript 3 C O O superscript negative sign bar. Above these two bars is the phrase, “Buffer solution after addition of strong base.” From the middle bars again, there is an arrow that points left. The arrow is labeled, “Add H subscript 3 O superscript positive sign.” This arrow points to two bars again, but this time the C H subscript 3 C O O H bar is taller than the C H subscript 3 C O O superscript negative sign bar. These two bars are labeled, “Buffer solution after addition of strong acid.”
Figure 2. When H3O+ is added to a buffer solution the weak base is converted to weak conjugate acid; when OH– is added to the buffer solution the weak acid is converted to weak conjugate base.

The buffer solution moderates changes in pH because it consists of both a weak acid (that can react with added strong base) and a weak base (that can react with strong acid). The weak base and weak acid need to be a conjugate pair so that when they react with each other the concentrations of weak base and weak acid do not change.

The pH of a buffer solution can be calculated from the Ka of the weak acid. For example, for a solution with 0.10 M acetic acid and 0.10 M sodium acetate initially, this ICE table can be set up. (Because the initial concentration of H3O+ is very small, the reaction goes from left to right.)
This table has two main columns and four rows. The first row for the first column does not have a heading and then has the following in the first column: Initial concentration ( M ), Change ( M ), Equilibrium ( M ). The second column has the header of “[ C H subscript 3 C O subscript 2 H ] [ H subscript 2 O ] equilibrium arrow H subscript 3 O superscript plus sign [ C H subscript 3 C O subscript 2 superscript negative sign ].” Under the second column is a subgroup of four columns and three rows. The first column has the following: 0.10, negative x, 0.10 minus sign x. The second column is blank. The third column has the following: approximately 0, x, x. The fourth column has the following: 0.10, x, 0.10 plus sign x.

[latex]K_\text{c} =  K_{\text{a, acetic acid}} \;\;\;\text{and}\;\;\dfrac{x(0.10\;+\;x)}{0.10\;-\;x} = 1.8\;\times\;10^{-5}[/latex]

Either solve the quadratic equation or make the approximation that x << 0.10 and simply the equilibrium constant expression to:

[latex]\dfrac{x(0.10)}{0.10} = 1.8\;\times\;10^{-5}[/latex]

Both approaches give x = 1.8 × 10-5. Therefore, [H3O+] = 1.8 × 10-5 M and the pH of this buffer solution is

pH = -log[H3O+] = -log(1.8 × 10-5) = 4.74

Note that using the initial condition of [H3O+] = 1.0 × 10-7 M would yield [H3O+]eq = 1.0 × 10-7 + x. Within the two significant figures involved in the above calculations, [H3O+] is still 1.8 × 10-5 M.

Exercise 1: Characteristics of Buffer Solutions

D36.2 Henderson-Hasselbalch Equation

The ionization constant expression for a weak acid HA is:

[latex]K_{\text{a}} = \dfrac{[\text{H}_3\text{O}^{+}][\text{A}^{-}]}{[\text{HA}]}[/latex]

Rearranging gives:

[latex][\text{H}_3\text{O}^{+}] = K_{\text{a}}\;\times\;\dfrac{[\text{HA}]}{[\text{A}^{-}]}[/latex]

Taking the negative logarithm of both sides, we have:

[latex]-\text{log}[\text{H}_3\text{O}^{+}] = -\text{log}\;K_{\text{a}}\;-\;\text{log}\dfrac{[\text{HA}]}{[\text{A}^{-}]}[/latex]

When preparing a buffer solution it is convenient to deal with the initial concentrations of the weak acid and weak base. Thus

[latex]\text{pH} = \text{p}K_{\text{a}}\;-\;\text{log}\dfrac{(\text{initconcHA})\;-\;x}{(\text{initconcA}^{-})\;+\;x}[/latex]

In this equation x is the increase in concentration of H3O+ as the solution reaches equilibrium (see Section D36.1 above) and (initconcHA) and (initconcA−) are the concentration of HA and A− before any reaction occurs. When the assumptioin is made that x is at least 100 times smaller than the concentrations of HA and A− and the last term on the right is inverted, changing the sign of the logarithm, we have the Henderson-Hasselbalch equation:

[latex]\text{pH} = \text{p}K_{\text{a}}\;+\;\text{log}\dfrac{(\text{initial concentration of weak base})}{(\text{initial concentration weak acid})}[/latex]

The Henderson-Hasselbalch equation can be used to calculate the pH, given the Ka of a weak acid and the initial concentrations of the weak acid and its conjugate base in a buffer solution. Or it can be used to determine the ratio of initial concentrations of weak acid and base required to achieve a desired pH.

The “x is small” approximation must be valid to use this equation and the equation applies only to buffer solutions in which the ratio [latex]\frac{(\text{initial concentration of weak base})}{(\text{initial concentration weak acid})}[/latex] is between 0.1 and 10. Adding enough strong acid or strong base to exceed this range begins to change the pH significantly.

Exercise 2: Using the Henderson-Hasselbalch Equation to Calculate pH

Using the Henderson-Hasselbalch equation, calculate the pH of a buffer solution containing 0.30 M CH3COOH and 0.20 M CH3COONa.  (The Ka of acetic acid is 1.80 x 10-5 M)

D36.3 Selection of a Suitable Buffer

A buffer solution moderates changes in pH because it contains both a weak acid (to react with added strong base) and a weak base (to react with added strong acid). According to the Henderson-Hasselbalch equation, if the concentrations of weak acid and weak base are equal, the pH of the buffer solution equals the pKa of the weak acid involved. This leads to several criteria for a suitable buffer solution.

  1. A buffer solution should have approximately equal concentrations of the weak acid and weak base. A buffer solution has significantly less resistance to a change in pH when the ratio [weak base] / [weak acid] is greater than 10 or less than 0.1. Figure 3 shows the pH of an acetic acid-acetate ion buffer as strong base is added. The initial pH is 4.74. A change of 1 pH unit occurs when [acetic acid] / [acetate ion] = 0.11 (acetic-acid concentration is 11% of acetate-ion concentration).
    A graph is shown with a horizontal axis labeled “Added m L of 0.10 M N a O H” which has markings and vertical gridlines every 10 units from 0 to 110. The vertical axis is labeled “p H” and is marked every 1 unit beginning at 0 extending to 11. A break is shown in the vertical axis between 0 and 4. A red curve is drawn on the graph which increases gradually from the point (0, 4.8) up to about (100, 7) after which the graph has a vertical section up to about (100, 11). The curve is labeled [ C H subscript 3 C O subscript 2 H ] is 11 percent of [ C H subscript 3 CO subscript 2 superscript negative].
    Figure 3. The graph, an illustration of buffering action, shows change of pH as an increasing amount of a 0.10-M NaOH solution is added to 100 mL of a buffer solution in which, initially, [CH3COOH] = [CH3COO−] = 0.10 M.
  2. The larger the concentrations of weak acid and weak base in a buffer solution are the greater the amount of strong acid or strong base that can be added (to a given volume of solution) before there is a significant change in pH.
  3. When designing a buffer system, look for weak conjugate acid-base pairs that have pKa of the acid near the desired pH. Then adjust the ratio [weak base] / [weak acid] to achieve the exact pH desired.

Example 1

Choosing an Appropriate Buffer System
You need a buffer solution with pH = 6.94. In the lab, these solutions are available: 0.100-M acetic acid; 0.100-M sodium acetate; 0.100-M lactic acid; 0.100-M sodium lactate; 0.100-M sodium dihydrogen phosphate; 0.100-M disodium monohydrogen phosphate. Choose an appropriate acid-base pair for the buffer solution and describe how 100. mL of the buffer solution could be prepared in the laboratory. Ka values for the acids are acetic acid, 1.8 × 10−5 M; lactic acid, 1.4 × 10−4 M; dihydrogen phosphate ion, 6.3 × 10−8 M. (Assume solution volumes are additive.)

Solution
First, decide which acid-base pair to use, then calculate the appropriate ratio of base to acid, and finally figure out what volume of each solution to use to achieve the desired ratio.

The pKa of the acid should be close to the desired pH, so calculate the pKa of each acid: acetic acid, pKa = −log(1.8 × 10−5) = 4.74; lactic acid, pKa = −log(1.4 × 10−4) = 3.85; dihydrogen phosphate ion, pKa = −log(6.3 × 10−8) = 7.20. Because dihydrogen phosphate ion has pKa that differs from the desired pH by less than 1, the dihydrogen phosphate / hydrogen phosphate buffer is the best choice.

The Henderson-Hasselbalch equation can be used to calculate the ratio (initconcHPO42−) / (initconcH2PO4−).

[latex]6.94 = 7.20\;+\;\text{log}\dfrac{(\text{initial concentration of weak base})}{(\text{initial concentration weak acid})}[/latex]

[latex]\text{log}\dfrac{(\text{initial concentration of weak base})}{(\text{initial concentration weak acid})}\;=\;6.94 - 7.20\;=\;-0.33[/latex]

[latex]\dfrac{(\text{initial concentration of weak base})}{(\text{initial concentration weak acid})}\;=\;10^{-0.33} = 0.47[/latex]

Because the concentrations of hydrogen phosphate ion and dihydrogen phosphate ion are equal, and because 100 mL total solution is needed,

Vbase = 0.47 Vacid          Vbase + Vacid = 100. mL

0.47 Vacid + Vacid = 100 mL          and          Vacid = 68 mL          Vbase = 32 mL

Therefore, to make the buffer solution, add 68 mL 0.100-M sodium dihydrogen phosphate and 32 mL 0.100-M disodium hydrogen phosphate to a beaker and stir thoroughly.

Check Your Learning
Look up Ka values in the Appendix and use them to decide which weak acid and its conjugate base is best to prepare a buffer solution with pH = 6.0. Available weak acids are hypochlorous acid, acetic acid, and carbonic acid.

Answer:

H2CO3

D36.4 Buffer Capacity

We can see how a buffer solution works by comparing quantitatively the pH of a buffered solution with the pH of a unbuffered solution upon addition of a strong acid or base.

For example, calculate the pH change upon the addition of 1.0 mL of 0.10 M NaOH to 100 mL of a buffer solution containing 0.10 M acetic acid and 0.10 M sodium acetate. The pH of the initial buffer solution is:

[latex]\text{pH}\;=\;\text{p}K_\text{a}\;+\;\text{log}\dfrac{[A^-]}{[HA]}\;=\;4.74\;+\;0\;=\;4.74[/latex]

Assume that all the NaOH (a strong base) reacts in the solution:

                                          NaOH(aq) + CH3COOH(aq) → CH3COONa(aq) + H2O(l)
initial amount (mol):         0.00010          0.010                       0.010
final amount (mol):                 0               0.0099                    0.0101
final concentration (M):         0               0.098                        0.10

Hence, the pH of the final solution is:

[latex]pH\;=\;pK_a\;+\;\text{log}\dfrac{[A^-]}{[HA]}\;=\;4.74\;+\;\text{log}\dfrac{0.10\;M}{0.098\;\text{M}}\;=\;4.75[/latex]

Now consider how much the pH changes when we add 1.0 mL of 0.10 M NaOH to 100 mL of 1.8 × 10-5 M HCl solution (pH = 4.74). All of the 1.8 × 10-6 moles of HCl reactwith NaOH, leaving behind

1.0 × 10-4 mol – 1.8 × 10-6 mol = 9.8 × 10-5 mol NaOH

which gives the resulting solution a pOH of:

[latex]\text{pOH}\;=\;-\text{log}\left(\dfrac{9.8\;\times\;10^{-5}\;\text{mol}}{0.101\;\text{L}}\right)\;=\;3.01[/latex]

Or a pH of 14.00 − 3.01 = 10.99. Hence, in the unbuffered solution, the pH changed from 4.74 to 10.99 upon the addition of 1.0 mL of 0.10 M NaOH, while in the buffer solution, the pH changed from 4.74 to 4.75.

However, buffer solutions do not have an unlimited capacity to keep the pH relatively constant (Figure 4). If we add so much base to a buffer that all the weak acid reacts, no more buffering action toward the base is possible. Similarly, if we add an excess of acid, the weak base would all be reacted, and no more buffering action toward any additional acid would be possible. In fact, we do not even need to react away all the acid or base in a buffer to make significant change in pH it: buffering action diminishes rapidly as a given component nears depletion. This was seen in Figure 3 above, where reducing the concentration of weak acid to 11% of the concentration of weak base caused a change of 1 pH unit. The curve in Figure 3 goes up rapidly after that, indicating that the buffer has been “broken” and no longer resists changes in pH.

No Alt Text
Figure 4. Adding acid to a buffer solution. The color of the indicator (methyl orange) shows that a small amount of acid added to a buffered solution of pH 8 (beaker on the left) has little effect on the pH of the buffer (middle beaker). However, a large amount of acid exhausts the buffering capacity of the solution and the pH changes dramatically (beaker on the right). (credit: modification of work by Mark Ott)

The buffer capacity is the amount (mol) of acid or base that can be added to a given volume of a buffer solution before the pH changes by ±1 from the pKa. (Recall that if equal concentrations of weak acid and conjugate base are in a buffer solution, pH = pKa.) Buffer capacity depends on the amounts of the weak acid and its conjugate base that are in a buffer mixture. For example, 1 L of a solution that is 1.0 M in acetic acid and 1.0 M in sodium acetate has a greater buffer capacity than 1 L of a solution that is 0.10 M in acetic acid and 0.10 M in sodium acetate even though both solutions have the same pH. The first solution has more buffer capacity because it contains more acetic acid and acetate ion.

It takes 0.82 moles of HCl to change the buffer pH from 4.74 to 3.74 in the first solution:

[latex]3.74\;=\;4.74\;+\;\text{log}\dfrac{[A^-]}{[HA]}[/latex]
[latex]\dfrac{[\text{A}^-]}{[\text{HA}]}\;=\;10^{-1}\;=\;0.1\;=\;\dfrac{(1.0\;\text{mol}\;-\;x)/(1\;\text{L})}{(1.0\;\text{mol}\;+\;x)/(1\;\text{L})}[/latex]

(Note that because both weak base and weak acid are in the same solution volume, the volume cancels out and we can use the amount (mol) of acetic acid and acetate in the [latex]\frac{[A^-]}{[HA]}[/latex] term.) Solving the equation gives x = 0.82.

On the other hand, for the solution where the concentrations of weak acid and conjugate base are 0.10 M, it takes only 0.082 mol HCl to change the buffer pH from 4.74 to 3.74:

[latex]\dfrac{[\text{A}^-]}{[\text{HA}]}\;=\;10^{-1}\;=\;0.1\;=\;\dfrac{0.1\;\text{mol}\;-\;x}{0.1\;\text{mol}\;+\;x}\;\;\;\;\;x\;=\;0.082[/latex]
If a buffer solution does not have equal concentrations of weak acid and weak base, the buffer capacity when strong acid is added is different from the buffer capacity when strong base is added.

Example 2

Buffer Capacity
A buffer solution is prepared by mixing 35.0 mL 0.100-M lactic acid and 65.0 mL 0.100-M sodium lactate. Calculate the pH of the buffer solution, the buffer capacity for added strong acid, and the buffer capacity for added strong base. Ka = 1.4 × 10−4 M for lactic acid. Assume solution volumes are additive.

Solution
Plan: Abbreviate lactic acid as HL and lactate ion as L−. Calculate the amount (mol) of each solute and divide by the total volume of 100.0 mL to calculate initial concentrations of HL and L−. Use the Henderson-Hasselbalch equation to calculate the pH of the buffer solution. Then calculate the amount of acid needed to lower the pH by 1 pH unit from the pKa and the amount of base needed to raise the pH by 1 pH unit.

Initial amount of HL = (0.0350 L × 0.100 mol/L)  = 3.5 × 10−3 mol

Initial concentration of HL = (3.5 × 10−3 mol)/(0.100 L) = 3.5 × 10−2 M

Initial amount of L− = (0.0650 L × 0.100 mol/L)  = 6.5 × 10−3 mol

Initial concentration of L− = (6.5 × 10−3 mol)/(0.100 L) = 6.5 × 10−2 M

pKa = −log(1.4 × 10−4) = 3.85

[latex]\text{pH} = \text{p}K_{\text{a}}\;+\;\text{log}\dfrac{(\text{initconcL}^-)}{(\text{initiconcHL})}\;=\;3.85\;+\;\text{log}\dfrac{(6.5\times 10^{-2})}{(3.5\times 10^{-2})}\;=\;4.12[/latex]

Let x be the amount of strong acid added to lower the pH to 1 pH unit below pKa = 3.85. Then

[latex]\dfrac{[\text{L}^-]}{[\text{HL}]}\;=\;10^{(2.85-3.85)}\;\;=\;10^{-1.00}\;=\;0.100\;=\;\dfrac{0.00650\;\text{mol}\;-\;x}{0.00350\;\text{mol}\;+\;x}\;\;\;\;\;x\;=\;0.0056[/latex]

Let y be the amount of strong base added to raise the pH to 1 pH unit above pKa = 3.85. Then

[latex]\dfrac{[\text{L}^-]}{[\text{HL}]}\;=\;10^{(4.85-3.85)}\;\;=\;10^{1.00}\;=\;10.0\;=\;\dfrac{0.00650\;\text{mol}\;+\;y}{0.00350\;\text{mol}\;-\;y}\;\;\;\;\;y\;=\;0.0026[/latex]

Thus the buffer pH = 4.12. It requires 0.0056 mol strong acid to reach the buffer capacity and 0.0026 mol strong base to reach the buffer capacity.

Check Your Learning
Write a scientific explanation for each of these facts:

  1. The pH of the buffer is larger than the pKa.
  2. The amount of strong acid needed to exceed the buffer capacity is larger than the amount of strong base needed to exceed the buffer capacity.

Answer:

  1. There is more weak base in the buffer solution than weak acid. Therefore the buffer is more basic than if there were equal concentrations of weak base and weak acid. More basic means higher pH.
  2. Weak base reacts with strong acid to maintain nearly constant pH. Because the amount of weak base is greater than the amount of weak acid the buffer has greater capacity to react with added strong acid.

Podia Question

A solution is prepared by adding 50.0 mL 0.50-M acetic acid and 50.0 mL 0.30-M NaOH to a beaker and stirring. Is this solution a buffer solution? If so, calculate the pH of the buffer. If not, explain why the solution does not resist change in pH when 1.0 mL 0.5-M HCl is added.

Two days before the next whole-class session, this Podia question will become live on Podia, where you can submit your answer.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chemistry 109 Copyright © by John Moore; Jia Zhou; and Etienne Garand is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.