As you work through this section, if you find that you need a bit more background material to help you understand the topics at hand, you can consult “Chemistry: The Molecular Science” (5th ed. Moore and Stanitski) Chapter 15-2, and/or Chapter 16.5-16.8 in the Additional Reading Materials section.

D37.1 Titration

In a titration, one solution is added to a second solution in a way that allows the quantity of each solution to be measured accurately. A chemical reaction occurs between solutes in the two solutions and exactly enough of the first solution is added to react completely with the second solution. Typically, one solution is added from a buret, a calibrated glass tube with a stopcock at the bottom (Figure 1). The buret allows additions of very small increments of volume and determination of the total volume added. The solution added from the buret is the titrant.  Titrant is added to a carefully measured volume of a second solution in a flask or beaker. When just enough titrant has been added for complete reaction with the second solution, the equivalence point of the titration has been reached. From the balanced chemical equation for the titration reaction, the volume of each solution at the equivalence point, and the concentration of one of the two solutions, the concentration of the other solution can be determined.

The equivalence point of a titration may be detected visually if a distinct change in the appearance of the sample solution accompanies the completion of the reaction. For example, in the titration of oxalic acid with potassium permanganate, the reaction is

5 H₂C₂O₄(aq)  +  2 MnO₄⁻(aq)  +  6 H⁺(aq)  →  10 CO₂(g)  +  2 Mn²⁺(aq)  + 8 H₂O(l)

Permanganate ion is purple and all other species are colorless. If the permanganate solution is delivered from a buret to oxalic acid in a flask, the flask is colorless until all the oxalic acid has reacted with permanganate. The next tiny increment of permanganate solution causes a pale purple color in the flask because there is no more oxalic acid to react with permanganate and remove the color. More commonly, a special dye called an indicator is added to the solution being titrated to provide a color change at or very near the equivalence point. Equivalence points may also be detected by measuring some solution property that changes in a predictable way during the course of the titration, such as pH.

Regardless of the approach taken to detect a titration’s equivalence point, the volume of titrant actually measured is called the end point. Properly designed titration methods typically ensure that the difference between the equivalence and end points is negligible. Though any type of chemical reaction may serve as the basis for a titration analysis, precipitation, acid-base, and oxidation-reduction titrations are most common.

D37.2 Titration Curves

Titrations can be used to analyze solutions quantitatively for their acid or base concentrations because pH changes rapidly near the equivalence point. Acid-base indicators change color over a range of about 2 pH units, so if pH increases (or decreases) by 2 or more pH units when 0.01 mL titrant is added at the equivalence point, the color change signals the end point of the titration.

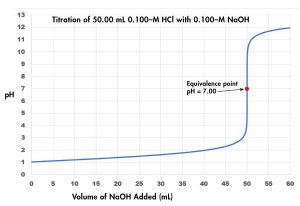
Figure 2 shows a graph of pH as a function of volume of titrant, a titration curve, for the titration of a 50.0-mL sample of 0.100-M hydrochloric acid with 0.100-M sodium hydroxide. The pH increases slowly at first, increases rapidly when nearly 50.0 mL NaOH has been added, and then increases slowly again. The point of inflection (steepest slope) is the equivalence point for the titration, and indicates when stoichiometrically equivalent quantities of acid and base are present. For the titration of a strong acid with a strong base, the equivalence point occurs at pH = 7.00.

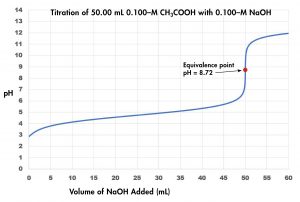
Now consider the titration of 50.00 mL of 0.100-M acetic acid (a weak acid) with 0.100-M sodium hydroxide (Figure 3) and compare the titration curve with that of the strong acid. Although the initial volumes and concentrations of the acids are the same, the pH for acetic acid, a weak acid, begins at a higher value (less acidic) and maintains higher pH values up to the equivalence point. This is because acetic acid is only partially ionized. The pH at the equivalence point is also higher (8.72 rather than 7.00) due to the presence of acetate, a weak base that raises the pH:

After the equivalence point, the two curves are identical because the pH depends only on the excess hydroxide ion in both cases.

D37.3 Acid-Base Indicators

Certain organic substances change color in dilute solution when [H₃O⁺] reaches a particular value. These substances, either weak organic acids or weak organic bases, are called acid-base indicators, and can be used to determine the pH of a solution. For example, phenolphthalein is colorless in an aqueous solution with [H₃O⁺] > 5.0 × 10⁻⁹ M (pH < 8.3), and turns red or pink when pH > 8.3.

The equilibrium in a solution of the acid-base indicator methyl orange, a weak acid, can be represented by an equation in which we use HIn as a simple representation for the complex methyl orange molecule:

The anion of methyl orange, In⁻, is yellow, and the nonionized form, HIn, is red. When we add acid to a solution of methyl orange, the increased hydronium ion concentration shifts the equilibrium toward the nonionized red form, in accordance with Le Châtelier’s principle. If we add base, we shift the equilibrium towards the yellow form. This behavior is analogous to the action of buffers.

An indicator’s color is the visible result of the ratio of the concentrations of the two species, In⁻ and HIn. If most of the indicator is present as In⁻, then we see the color of the In⁻ ion: yellow for methyl orange. If most is present as HIn, then we see the color of the HIn molecule: red for methyl orange. We can rearrange the equation for K_a and write:

When [H₃O⁺] = K_a, the ratio of [In⁻] to [HIn] is equal to 1, meaning that 50% of the indicator is present in the red form (HIn) and 50% is in the yellow ionic form (In⁻), and the solution appears orange in color. When [H₃O⁺] increases to 8 × 10⁻⁴ M (pH = 3.1), the solution turns red. No change in color is visible for further increase in [H₃O⁺]. At [H₃O⁺] = 4 × 10⁻⁵ M (pH = 4.4), most of the indicator is in the yellow ionic form, and further decrease in [H₃O⁺] does not produce a visible color change. The pH range between 3.1 (red) and 4.4 (yellow) is the color-change interval of methyl orange; the pronounced color change takes place between these pH values.

There are many different acid-base indicators. Their color changes have a wide range of pH values (Figure 4). Universal indicators and pH paper contain a mixture of indicators and exhibit different colors at different pH values.

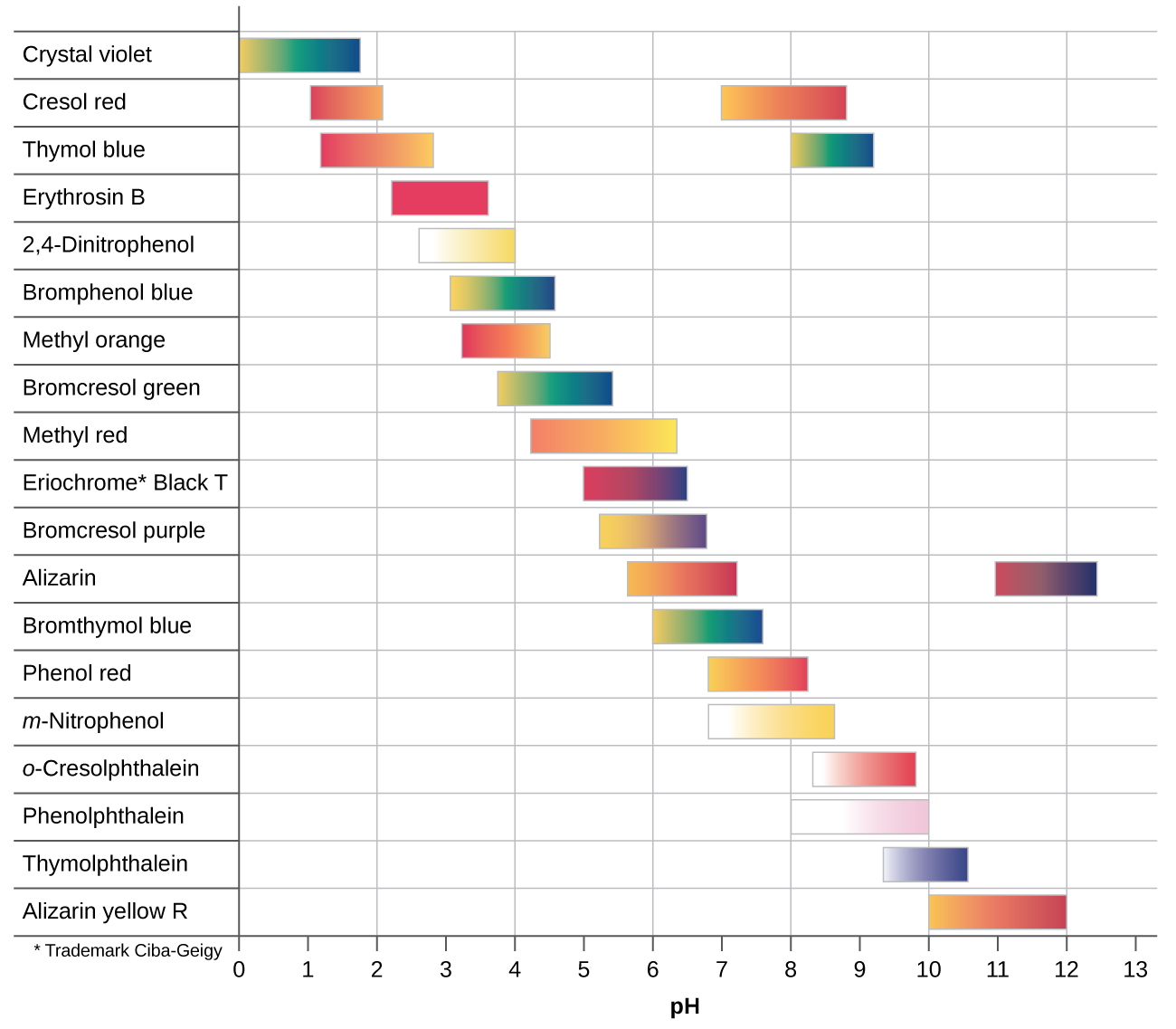
Titration curves can help us in selecting an indicator that will provide a sharp color change at the equivalence point. The best selection is an indicator with a color change interval that brackets the pH at the equivalence point of the titration.

The color change intervals of three indicators are shown in Figure 5. The vertical parts of the titration curves of both the titration of HCl and of CH₃COOH are located in the color-change interval of phenolphthalein. We can use it for titrations of either acid with strong base.

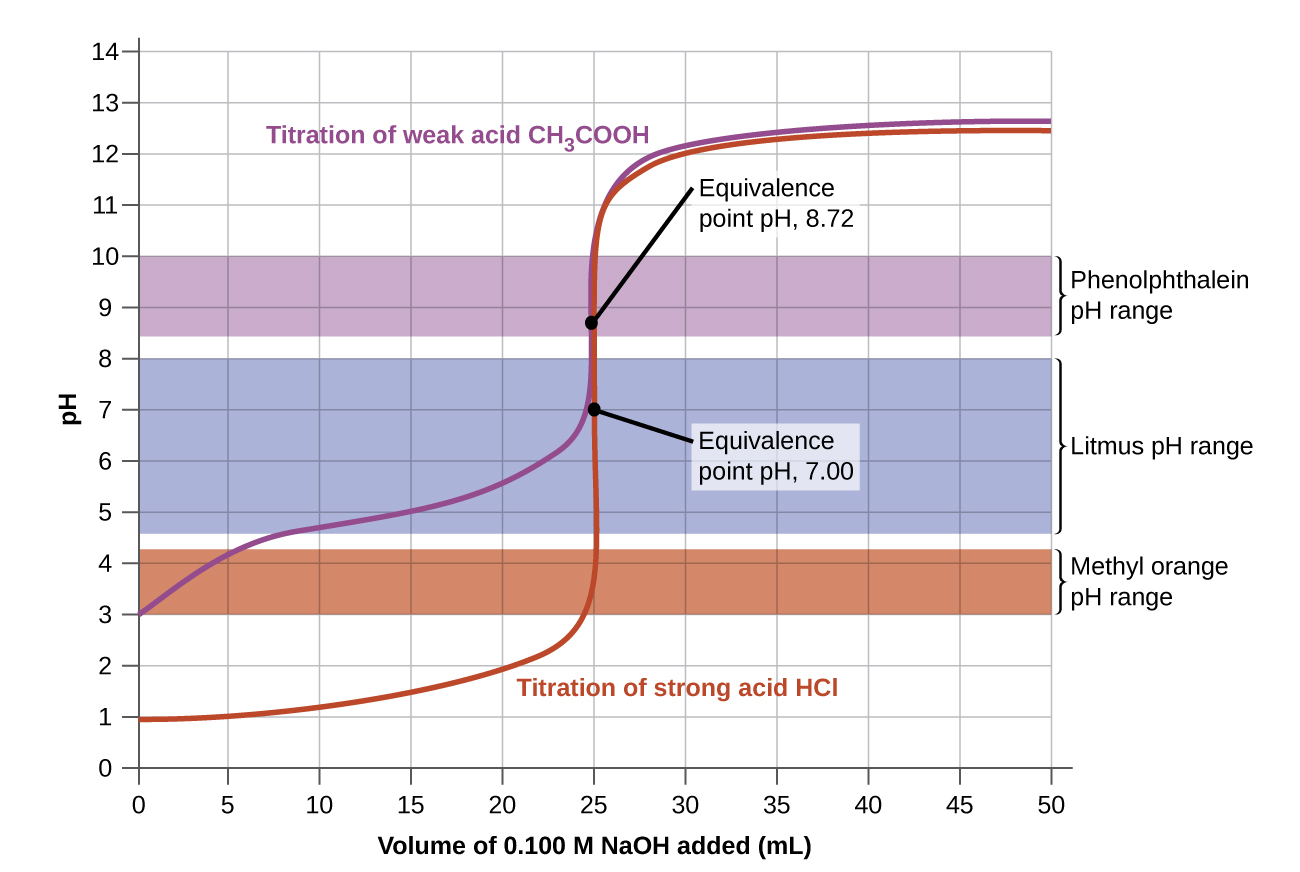
Litmus is a suitable indicator for the HCl titration. However, we should not use it for the CH₃COOH titration because the pH is within the color-change interval of litmus when only 12 mL of NaOH has been added, and it does not leave the range until 25 mL has been added. The color change would be very gradual, taking place during the addition of 13 mL of NaOH, making litmus useless as an indicator of the equivalence point.

We could use methyl orange for the HCl titration, but it would not give very accurate results: (1) It completes its color change slightly before the equivalence point is reached (but very close to it, so this is not too serious); (2) it changes color, as Figure 5 shows, during the addition of nearly 0.5 mL of NaOH, which is not so sharp a color change as that of litmus or phenolphthalein. Additionally, the color change, from yellow to orange to red, is not as visually distinct as the colorless to pink change of phenolphthalein. Methyl orange would be completely useless as an indicator for the CH₃COOH titration. Its color change begins after 1 mL of NaOH has been added and ends when about 8 mL has been added. The color change is completed long before the equivalence point is reached and hence provides no indication of the equivalence point.

We can also base our choice of indicator on the calculated pH at the equivalence point, which the pH of a solution of the salt resulting from the titration.

D37.4 Equilivalence point and midpoint

The equivalence point of a titration is where the amount (mol) of titrant added is in the stoichiometric mole ratio to the amount of solution being titrated. The midpoint of a titration is when we have added half the volume of titrant needed to reach the equivalence point. Suppose we are titrating a weak acid with strong base. At the midpoint, the pH of the solution equals the pK_a of the weak acid because we have added half the amount of strong base needed to react with all the weak acid. Therefore, half the weak acid has been converted to its conjugate base and half is unreacted and the concentrations of weak acid and conjugate base are equal. According to the Henderson-Hasselbalch equation,

[latex]\text{pH} = \text{p}K_{\text{a}}\;+\;\text{log}\dfrac{(\text{initial concentration of weak base})}{(\text{initial concentration weak acid})}[/latex]

Because the solution is a 50:50 mixture of weak acid and weak base,

pH = pK_a + log(1) = pK_a + 0 = pK_a

D37.5 Titration of Polyprotic Acids and Bases

When a weak polyprotic acid is titrated, there is more than a single equivalence point. For example, when H₂SO₃ is titrated with NaOH, there are two equivalence points because there are two acidic H atoms that can be removed from the H₂SO₃ molecule. There are also as many midpoints as there are equivalence points.

When a strong monoprotic base is added to a solution of a polyprotic acid, the neutralization reaction occurs in stages. The most acidic group is titrated first, followed by the next most acidic, and so forth. If the pKa values are separated by at least three pK_a units, then the overall titration curve shows well-resolved “steps” corresponding to the titration of each acidic proton.

As an example, consider the titration of a generic weak polyprotic acid H₃A with NaOH. Because there are three acidic protons in H₃A, there should be three equivalence points. Figure 6 shows the titration curve up to the point where 1 mol NaOH has been added per mole of H₃A in the solution being titrated. That is, up to the first equivalence point. The equilibrium involved is

H₃A(aq) + H₂O(l) ⇌ H₃O⁺(aq) + H₂A⁻(aq)

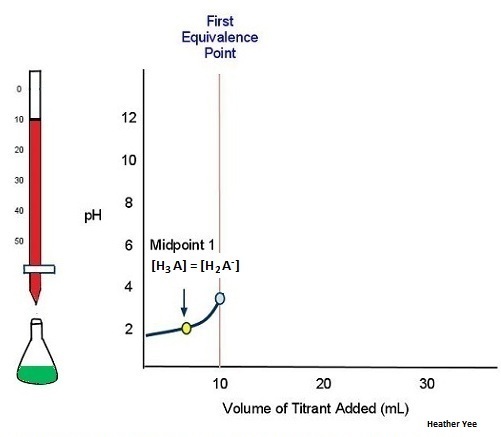
As more titrant is added, the titration curve crosses another midpoint and reaches the second equivalence point (Figure 7):

H₂A⁻(aq) + H₂O(l) ⇌ H³O⁺(aq) + HA²⁻(aq)

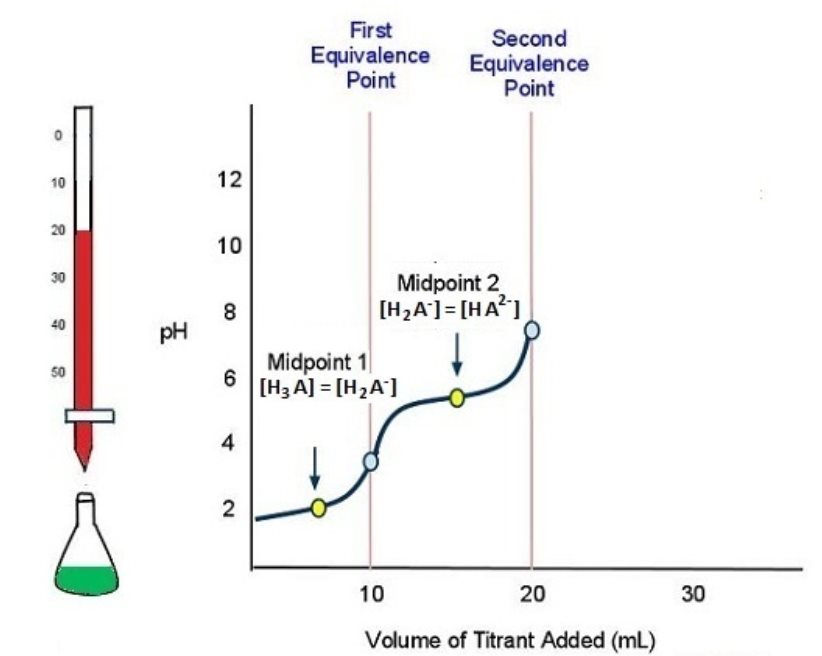
The titration is finally complete when all three equivalence points have been reached (Figure 8).

HA^2-(aq) + H₂O(l) ⇌ H₃O⁺(aq) + A³⁻(aq)

Even though an acid has two or more ionizable protons it is not always possible to detect all of the equivalence points. An actual titration of the triprotic acid H₃PO₄ with NaOH is illustrated in Figure 9. It shows two well-defined steps: the first midpoint corresponds to pK_a,1, and the second midpoint corresponds to pK_a,2. Because HPO₄²⁻ is such a weak acid, pK_a,3 has such a high value that the third step cannot be resolved using 0.100 M NaOH as the titrant.

The titration curve for the reaction of a polyprotic base with a strong acid is the mirror image of the curves shown above. The initial pH is high; as acid is added, the pH decreases in steps if the successive pK_b values are well separated.