Unit Four
Day 38: Oxidation-Reduction (Redox) Reactions
As you work through this section, if you find that you need a bit more background material to help you understand the topics at hand, you can consult “Chemistry: The Molecular Science” (5th ed. Moore and Stanitski) Chapter 3-5, 17-1 and 17-2, and/or Chapter 16.9 and Chapter 17.1-17.3 in the Additional Reading Materials section.
D38.1 Electrochemistry
Electrochemistry deals with chemical reactions that produce electricity and chemical reactions caused by passage of electrical current through matter. The reactions involve transfer of electron density. Such reactions are called oxidation-reduction (or redox) reactions. Many metals may be purified or electroplated using electrochemical methods. Batteries use chemical reactions that produce electricity spontaneously and electricity can do useful work.
The SI unit of electric charge is the coulomb, symbol C. The elementary unit of charge is the charge of an electron, 1.602 × 10−19 C. Movement of electrons or ions carries electric charge from one place to another. Electric current is the quantity of charge transferred per unit time, with SI unit ampere, symbol A, the transfer of one coulomb per second (1 A = 1 C/s). Typically, electric current flows in a closed path, an electric circuit; it is necessary to maintain a closed circuit for current to flow. A flow of charge is caused by an electrical potential difference between two points in the circuit. Electrical potential, SI unit volt, symbol V, is the ability of an electric field to do work on a charge. When 1 coulomb of charge moves through a potential difference of 1 volt, it gains or loses 1 joule (J) of energy.
| Quantity | Definition | Measure or Unit |
|---|---|---|
| Electric charge | Charge of an electron | 1.602 × 10−19 C |
| Electric current | The movement of charge | ampere = A = C/s |
| Electric potential | work needed to move the charge | volt = V = J/C |
| Electric field | A force acting upon other charges in the vicinity, generated by the presence of an electric charge |
D38.2 Redox Reactions and Oxidation Number
Some redox reactions involve transfer of electrons between reactant atoms to yield ionic products. For example, formation of a crystal lattice of sodium chloride (a lattice of Na+ ions and Cl− ions) requires transfer of electrons from sodium atoms to chlorine atoms:
It is useful to represent the electron transfer in two steps, one in which electrons are lost and one in which electrons are gained. These steps are called half-reactions. The half reactions for reaction of sodium with chlorine are
The half-reactions allow us to see that the number of electrons lost equals the number of electrons gained—we cannot create or destroy electrons in a chemical reaction. The half-reactions also show which species gains electrons (Cl atoms in Cl2) and which species loses electrons (Na atoms). The species that loses electrons is said to be oxidized and the loss of electrons is called oxidation; the species that gains electrons is said to be reduced and the gain of electrons is called reduction.
The species that causes reduction to occur is called the reducing agent (or reductant). In this reaction sodium is the reducing agent because it causes Cl2 to gain electrons. The species that causes oxidation to occur is called the oxidizing agent (or oxidant). In this reaction chlorine functions as an oxidant, causing sodium to lose electrons.
Some redox processes, however, do not involve obvious transfer of electrons. For example, when the product is a covalent compound, transfer of electrons to form ions is not involved:
To deal with such cases we define oxidation number (or oxidation state) of an element in a compound as the charge its atoms would possess if the compound was ionic, that is, if all electrons in each polar bond were assigned to the more electronegative atom. These stepwise rules can be used to assign oxidation numbers to each element in a compound.
-
-
- The oxidation number of an atom in an elemental substance is zero.
- The oxidation number of a monoatomic ion is equal to the ion’s charge.
- The sum of oxidation numbers over all atoms in a complete formula for a compound is zero.
- The sum of the oxidation numbers over all atoms in a polyatomic ion equals the ion's charge. If a compound includes more than one polyatomic ion, the oxidation number of an atom in one ion can differ from the oxidation number in the other polyatomic ion.
- Atoms of some elements have the same oxidation number in almost all compounds.
- Fluorine always has oxidation number −1 in its compounds
- Atoms of alkali metals (Li, Na, K, Rb, Cs) have oxidation number +1 in nearly all compounds
- Atoms of alkaline earth metals (Be, Mg, Ca, Sr, Ba) have oxidation number +2 in nearly all compounds
- Hydrogen has oxidation number +1 when combined with nonmetals, −1 when combined with metals
- Apply these two rules only if rules 1-5 have not determined all oxidation numbers.
- Oxygen has oxidation number −2 unless rules 1-5 have already given O a different oxidation number
- In binary compounds of nonmetals, the more electronegative element is given a negative oxidation number equal to the charge on its monoatomic ion; for example in PCl3, the more electronegative Cl is assigned oxidation number −1 and P is assigned +3 (by rule 3).
-
Example 1
Assigning Oxidation Numbers
Follow the guidelines above to assign oxidation numbers to all the elements in each formula:
(a) KNO3
(b) AlH3
(c) NH4NO3
(d) H2PO4−
Solution
Apply the rules in sequence.
(a) Rules 1 and 2 do not apply. Rule 3: oxidation numbers must sum to zero. Rule 5b: oxidation number of K is +1. Neither O or N has yet been defined to apply rule 6a: oxidation number of O is −2. Then (+1) + (x) + 3×(−2) = 0 so x = +5 and oxidation number of N is +5.
(b) Rule 3: oxidation numbers must sum to zero. Rule 5d: oxidation number of H is −1 because Al is a metal. Then (x) + 3×(−1) = 0 and oxidation number of Al is +3.
(c) This is an ionic compound containing NH4+ and NO3− ions. Rule 4: Assign oxidation numbers to atoms in each ion separately and the oxidation numbers sum to the ionic charge. For NH4+, rule 5d gives H oxidation number +1; then (x) + 4×(+1) = +1, x = −3 and oxidation number of N is −3. For NO3−, rule 6a says O is −2 so (x) + 3×(−2) = −1 and N is +5. (Note that the oxidation number of N is different in the two polyatomic ions.
(d) Rule 4: oxidation numbers sum to −1. Rule 5d: H is +1. Rule 6a: O is −2. Thus, 2×(+1) + (x) + 4×(−2) = −1 and P is +5.
Exercise 1: Assigning Oxidation Numbers
Sulfur can exist in many oxidation states. Determine the oxidation state of sulfur in each of the following species:
H2S; S8; SCl2; SO32-; K2SO4
(Don't forget that all oxidation states other than zero are either positive or negative and so need a "+" or "–" in front of the number as part of the state.)
Using oxidation numbers we can recognize oxidation-reduction (redox) reactions by looking for one or more elements whose oxidation numbers change. When its oxidation number increases, an element has been oxidized; when its oxidation number decreases, the element has been reduced.
In the 2 Na(s) + Cl2(g) ⟶ 2 NaCl(s) reaction, sodium is oxidized (its oxidation number increases from 0 in Na to +1 in NaCl) and chlorine is reduced (its oxidation number decreases from 0 in Cl2 to −1 in NaCl). In the H2(g) + Cl2(g) ⟶ 2 HCl(g) reaction, hydrogen is oxidized (its oxidation number increases from 0 in H2 to +1 in HCl) and chlorine is reduced (its oxidation number decreases from 0 in Cl2 to −1 in HCl).
Several subclasses of redox reactions are recognized, including combustion reactions in which the reductant (fuel) and oxidant (often, O2) react vigorously and produce significant quantities of heat, often in the form of a flame. A typical propellant reaction in which solid aluminum is oxidized by ammonium perchlorate is represented by this equation:
Exercise 2: Recognizing Oxidation-Reduction Reactions
Classify each reaction as oxidation-reduction, acid-base, or precipitation.
Optional: Watch a brief video showing the test firing of a small-scale, prototype, hybrid rocket engine planned for use in the new Space Launch System being developed by NASA. The first engines firing at 3 s (green flame) use a liquid fuel/oxidant mixture, and the second, more powerful engines firing at 4 s (yellow flame) use a solid mixture.
Example 2
Describing Redox Reactions
Identify which equations represent redox reactions. For those reactions identified as redox, name the oxidant and reductant.
(a) [latex]\text{ZnCO}_3(s) \longrightarrow \text{ZnO}(s) + \text{CO}_2(g)[/latex]
(b) [latex]2\text{Ga}(l) + 3\text{Br}_2(l) \longrightarrow 2\text{GaBr}_3(s)[/latex]
(c) [latex]2\text{H}_2 \text{O}_2(aq) \longrightarrow 2\text{H}_2 \text{O}(l) + \text{O}_2(g)[/latex]
(d) [latex]\text{BaCl}_2(aq) + \text{K}_2 \text{SO}_4(aq) \longrightarrow \text{BaSO}_4(s) + 2\text{KCl}(aq)[/latex]
(e) [latex]\text{C}_2 \text{H}_4(g) + 3\text{O}_2(g) \longrightarrow 2\text{CO}_2(g) + 2\text{H}_2 \text{O}(l)[/latex]
Solution
Redox reactions are identified if one or more elements undergo a change in oxidation number.
(a) This is not a redox reaction, since oxidation numbers remain unchanged for all elements.
(b) This is a redox reaction. Gallium is oxidized, its oxidation number increasing from 0 in Ga(l) to +3 in GaBr3(s). The reducing agent is Ga(l). Bromine is reduced, its oxidation number decreasing from 0 in Br2(l) to −1 in GaBr3(s). The oxidizing agent is Br2(l).
(c) This is a redox reaction. It is a particularly interesting process, as it involves the same element, oxygen, undergoing both oxidation and reduction (a so-called disproportionation reaction). Oxygen is oxidized, its oxidation number increasing from −1 in H2O2(aq) to 0 in O2(g). Oxygen is also reduced, its oxidation number decreasing from −1 in H2O2(aq) to −2 in H2O(l). For disproportionation reactions, the same substance functions as an oxidant and a reductant.
(d) This is not a redox reaction, since oxidation numbers remain unchanged for all elements.
(e) This is a redox reaction (combustion). Carbon is oxidized, its oxidation number increasing from −2 in C2H4(g) to +4 in CO2(g). The reducing agent (fuel) is C2H4(g). Oxygen is reduced, its oxidation number decreasing from 0 in O2(g) to −2 in H2O(l). The oxidizing agent is O2(g).
Check Your Learning
This equation describes the production of tin(II) chloride:
Is this a redox reaction? If so, identify the oxidant and reductant.
Answer:
Yes. Sn(s) is the reductant, HCl(g) is the oxidant.
Exercise 3: Recognizing Oxidizing and Reducing Agents
For the reaction below, identify which species is oxidized and which is reduced, and identify the oxidizing agent and the reducing agent.
[Enter your answers without subscripts, superscripts or states, and put charges in parentheses. For example, SO42- would be entered as SO4(2-).]
D38.3 Balancing Redox Reactions
Chemical equations for oxidation-reduction reactions are often difficult to balance. Splitting the process into half-reactions makes it easier because you can balance the oxidation “half” separately from the reduction “half”, make certain that the number of electrons lost in the oxidation equals the number of electrons gained in the reduction, and then sum the half-reaction to find the overall equation. Redox reactions frequently occur in solutions, which can be acidic, basic, or neutral. Because they are available in solution, both H3O+ ions and H2O(l) molecules may be reactants or products in acidic solution. Both OH− ions and H2O(l) molecules may be reactants or products in basic solution.
Acidic Solution
We will balance an example redox reaction in acidic solution and one in basic solution to highlight how the nature of the solution can play a role. (A neutral solution may be treated as acidic or basic, though treating it as acidic is usually easier.) Consider the unbalanced reaction:
Here, Fe2+ has lost an electron to become Fe3+; therefore, the iron underwent oxidation. The manganese underwent reduction; it gained five electrons to change from an oxidation state of +7 to an oxidation state of +2.
Reduction (unbalanced): MnO4¯(aq) ⟶ Mn2+(aq)
It is a useful simplification to represent H3O+ ions as H+(aq). In the example reaction, the reduction half-reaction involves oxygen, and we can use H+(aq) and H2O(l) to balance the elements O and H. Because there are four O atoms on the left side and none on the right, add 4 H2O(l) to the right. Then, to balance H atoms, add 8 H+(aq) on the left:
Once the atoms have been balanced we need to make certain that the total electric charge is the same on each side of each half-reaction. The iron atoms in the oxidation half-reaction are already balanced, but there are two positive charges on the left and three on the right, so charge is unbalanced. We use electrons to balance the charge. Adding a single electron on the right side gives a balanced oxidation half-reaction:
You should check the half-reaction for the number of each atom type and the total charge on each side of the equation. The charges include the actual charges of the ions times the number of ions and the charge on an electron times the number of electrons.
Charge: Does (1 × (+2)) = (1 × (+3) + 1 × (-1))? Yes
If the atoms and charges balance, the half-reaction is balanced.
In oxidation half-reactions, electrons appear on the right side of the equation. Because iron was oxidized, iron is the reducing agent.
For the reduction half-reaction, we have balanced the atoms but we need to check for charge balance. The total charge on the reactant-side is (1 × (−1)) + (8 × (+1)) = +7; the total charge on the product-side is (1 × (+2)) + (4 × (0)) = +2. Therefore, it is necessary to add five negative charges, that is, five electrons, to the left side to achieve charge balance:
You should always do a final check that the half-reaction is balanced for each atom type and the charge.
Now that this half-reaction is balanced, it is easy to see it involves reduction because electrons were gained when MnO4− was reduced to Mn2+. In all reduction half-reactions, electrons appear on the left side. The species that was reduced, MnO4−, is the oxidizing agent.
We now have two balanced half-reactions:
The key to combining the half-reactions is the electrons: the number of electrons transferred from the oxidation half-reaction must equal the number of electrons transferred to the reduction half-reaction. In this example, the oxidation half-reaction generates one electron, while the reduction half-reaction requires five. The lowest common multiple of one and five is five; therefore, it is necessary to multiply every term in the oxidation half-reaction by five and every term in the reduction half-reaction by one. Multiplying each half-reaction by the appropriate factor and summing the resulting half-reactions gives:
This is the overall balanced equation in acidic solution. Electrons do not appear in the equation because all electrons lost in the oxidation are gained in the reduction. On each side of the overall equation there should be the same number of atoms of each kind and the same total electric charge. Be sure to carefully check each side to verify everything has been balanced correctly.
Basic Solution
In a basic solution, there is an excess of OH− ions instead of H3O+ ions. The simplest way to generate the balanced overall equation in basic solution is to start with the balanced equation in acidic solution, then “convert” it to the equation for basic solution. For example, balance this reaction in basic solution:
[latex]\text{MnO}_4^{-}(\text{aq})\;+\;\text{Cr(OH)}_3(\text{s})\;{\longrightarrow}\;\text{MnO}_2(\text{s})\;+\;\text{CrO}_4^{2-}(\text{aq})[/latex]
Start by collecting the species given into an unbalanced oxidation half-reaction and an unbalanced reduction half-reaction.
[latex]\begin{array}{rrcl} \text{oxidation (unbalanced):} & \text{Cr(OH)}_3(\text{s}) &\longrightarrow& \text{CrO}_4^{2-}(\text{aq}) \\[0.5em] \text{reduction (unbalanced):} & \text{MnO}_4^{-}(\text{aq}) &\longrightarrow& \text{MnO}_2(\text{s}) \end{array}[/latex]
Starting with the oxidation half-reaction, note that chromium atoms are already balanced:
[latex]\text{oxidation (unbalanced):}\;\text{Cr(OH)}_3(\text{s})\;{\longrightarrow}\;\text{CrO}_4^{2-}(\text{aq})[/latex]
If this were an acidic solution, we could use H+(aq) and H2O(l) to balance H and O. Adding one water molecule to the left side provides the necessary oxygen; to balance H we need five H+(aq) on the right side:
[latex]\text{oxidation (unbalanced):}\;\text{Cr(OH)}_3(\text{s})\;+\;\text{H}_2\text{O}(l)\;{\longrightarrow}\;\text{CrO}_4^{2-}(\text{aq})\;+\;5\;\text{H}^{+}(\text{aq})[/latex]
The left side of the equation has a total charge of [0], and the right side a total charge of [−2 + 5 × (+1) = +3]. The difference is three, adding three electrons to the right side produces a mass- and charge-balanced oxidation half-reaction (in acidic solution):
[latex]\text{oxidation (balanced, acidic): Cr(OH)}_3(\text{s})\;+\;\text{H}_2\text{O}(l)\;{\longrightarrow}\;\text{CrO}_4^{2-}(\text{aq})\;+\;5\text{H}^{+}(\text{aq})\;+\;3\text{e}^{-}[/latex]
Checking the half-reaction:
[latex]\text{Cr: Does}\;(1\;\times\;1) = (1\;\times\;1)\text{? Yes.} \\[0.5em] \text{H: Does}\;(1\;\times\;3\;+\;1\;\times\;2) = (5\;\times\;1)\text{? Yes.} \\[0.5em] \text{O: Does}\;(1\;\times\;3\;+\;1\;\times\;1) = (4\;\times\;1)\text{? Yes.} \\[0.5em] \text{Charge: Does}\;[0 = [1\;\times\;(-2)\;+\;5\;\times\;(+1)\;+\;3\;\times\;(-1)]\text{? Yes.}[/latex]
Now work on the reduction. On the left side there are four O atoms in the MnO4− ; on the right side there are two O atoms in MnO2. To balance O we need two water molecules on the right. Then to balance H we need to add four H+(aq) on the left.
[latex]\text{reduction (unbalanced):}\;\text{MnO}_4^{-}(\text{aq})\;+\;4\;\text{H}^{+}(\text{aq})\;{\longrightarrow}\;\text{MnO}_2(\text{s})\;+\;2\;\text{H}_2\text{O}(l)[/latex]
Then add three electrons to the left side to balance the charge:
[latex]\text{reduction (balanced, acidic):}\;\text{MnO}_4^{-}(\text{aq})\;+\;4\;\text{H}^{+}(aq)\;+\;3\;\text{e}^{-}\;{\longrightarrow}\;\text{MnO}_2(\text{s})\;+\;2\;\text{H}_2\text{O}(l)[/latex]
Make sure to check the half-reaction:
[latex]\text{Mn: Does}\;(1\;\times\;1) = (1\;\times\;1)\text{? Yes.} \\[0.5em] \text{H: Does}\;(4\;\times\;1) = (2\;\times\;2)\text{? Yes.} \\[0.5em] \text{O: Does}\;(1\;\times\;4) = (1\;\times\;2\;+\;2\;\times\;1)\text{? Yes.} \\[0.5em] \text{Charge: Does}\;[1\;\times\;(-1)\;+\;4\;\times\;(+1)\;+\;3\;\times\;(-1)] = [0]\text{? Yes.}[/latex]
Collecting what we have so far:
[latex]\begin{array}{lrcl} \text{oxidation:} & \text{Cr(OH)}_3(\text{s})\;+\;\text{H}_2\text{O}(l) &\longrightarrow& \text{CrO}_4^{2-}(aq)\;+\;5\;\text{H}^{+}(aq)\;+\;3\;\text{e}^{-} \\[0.5em] \text{reduction:} & \text{MnO}_4^{-}(aq)\;+\;4\;\text{H}^{+}(aq)\;+\;3\;\text{e}^{-} &\longrightarrow& \text{MnO}_2(\text{s})\;+\;2\;\text{H}_2\text{O}(l) \end{array}[/latex]
In this case, both half reactions involve the same number of electrons; therefore, simply add the two half-reactions together and simplify.
[latex]\text{MnO}_4^{-}(\text{aq})\;+\;4\;\text{H}^{+}(\text{aq})\;+\;\text{Cr(OH)}_3(\text{s})\;+\;\text{H}_2\text{O}(l)\;{\longrightarrow}\\[0.5em] \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{CrO}_4^{2-}(\text{aq})\;+\;\text{MnO}_2(\text{s})\;+\;2\;\text{H}_2\text{O}(l)\;+\;5\;\text{H}^{+}(\text{aq})[/latex]
[latex]\text{MnO}_4^{-}(\text{aq})\;+\;\text{Cr(OH)}_3(\text{s})\;{\longrightarrow}\;\text{CrO}_4^{2-}(\text{aq})\;+\;\text{MnO}_2(\text{s})\;+\;\text{H}_2\text{O}(l)\;+\;\text{H}^{+}(\text{aq})[/latex]
Checking each side of the equation:
[latex]\text{Mn: Does}\;(1\;\times\;1) = (1\;\times\;1)\text{? Yes.} \\[0.5em] \text{Cr: Does}\;(1\;\times\;1) = (1\;\times\;1)\text{? Yes.} \\[0.5em] \text{H: Does}\;(1\;\times\;3) = (2\;\times\;1\;+\;1\;\times\;1)\text{? Yes.} \\[0.5em] \text{O: Does}\;(1\;\times\;4\;+\;1\;\times\;3) = (1\;\times\;4\;+\;1\;\times\;2\;+\;1\;\times\;1)\text{? Yes.} \\[0.5em] \text{Charge: Does}\;[1\;\times\;(-1)] = [1\;\times\;(-2)\;+\;1\;\times\;(+1)]\text{? Yes.}[/latex]
This is the balanced equation in acidic solution. To "convert" to basic solution, add enough OH−(aq) to each side of the equation to react with all the H+(aq) on one side. This converts H+(aq) to H2O(l) on one side and adds OH−(aq) on the other side. Then simplify:
[latex]\text{OH}^{-}(\text{aq})\;+\;\text{MnO}_4^{-}(\text{aq})\;+\;\text{Cr(OH)}_3(\text{s})\;{\longrightarrow}\;\text{CrO}_4^{2-}(\text{aq})\;+\;\text{MnO}_2(\text{s})\;+\;\text{H}_2\text{O}(l)\;+\;(\text{H}^{+}\;+\;\text{OH}^{-})(\text{aq})[/latex]
[latex]\text{OH}^{-}(\text{aq})\;+\;\text{MnO}_4^{-}(\text{aq})\;+\;\text{Cr(OH)}_3(\text{s})\;{\longrightarrow}\;\text{CrO}_4^{2-}(\text{aq})\;+\;\text{MnO}_2(\text{s})\;+\;2\text{H}_2\text{O}(l)[/latex]
Checking each side of the equation:
[latex]\text{Mn: Does}\;(1\;\times\;1) = (1\;\times\;1)\text{? Yes.} \\[0.5em] \text{Cr: Does}\;(1\;\times\;1) = (1\;\times\;1)\text{? Yes.} \\[0.5em] \text{H: Does}\;(1\;\times\;1\;+\;1\;\times\;3) = (2\;\times\;2)\text{? Yes.} \\[0.5em] \text{O: Does}\;(1\;\times\;1\;+\;1\;\times\;4\;+\;1\;\times\;3) = (1\;\times\;4\;+\;1\;\times\;2\;+\;2\;\times\;1)\text{? Yes.} \\[0.5em] \text{Charge: Does}\;[1\;\times\;(-1)\;+\;1\;\times\;(-1)] = [1\;\times\;(-2)]\text{? Yes.}[/latex]
This is the balanced equation in basic solution.
Example 4
Balancing Oxidation-Reduction Reactions
Balance each reaction in acidic or basic solution as indicated.
(a) [latex]\text{H}_2(\text{g})\;+\;\text{Cu}^{2+}(\text{aq})\;{\longrightarrow}\;\text{Cu}(\text{s})\;\;\;\text{(acidic solution)}[/latex]
(b) [latex]\text{H}_2(\text{g})\;+\;\text{Cu(OH)}_2(\text{s})\;{\longrightarrow}\;\text{Cu}(\text{s})\;\;\;\text{(basic solution)}[/latex]
(c) [latex]\text{Fe}(\text{s})\;+\;\text{Ag}^{+}(\text{aq})\;{\longrightarrow}\;\text{Fe}^{2+}(\text{aq})\;+\;\text{Ag}(\text{s})[/latex]
(d) Identify the oxidizing agents in reactions (a), (b), and (c).
(e) Identify the reducing agents in reactions (a), (b), and (c).
Answer:
(a) [latex]\text{H}_2(g)\;+\;\text{Cu}^{2+}(\text{aq})\;{\longrightarrow}\;2\text{H}^{+}(\text{aq})\;+\;\text{Cu}(\text{s})[/latex]
(b) [latex]\text{H}_2(g)\;+\;\text{Cu(OH)}_2(\text{s})\;{\longrightarrow}\;2\text{H}_2\text{O}(l)\;+\;\text{Cu}(\text{s})[/latex]
(c) [latex]\text{Fe}(\text{s})\;+\;2\text{Ag}^{+}(\text{aq})\;{\longrightarrow}\;\text{Fe}^{2+}(\text{aq})\;+\;2\text{Ag}(\text{s})[/latex]
(d) The oxidizing agent is the species reduced: Cu2+, Cu(OH)2, Ag+
(e) The reducing agent is the species oxidized: H2, H2, Fe
D38.4 Introduction to Voltaic Cells
A voltaic cell (or galvanic cell) is an electrochemical cell in which a product-favored redox reaction produces an electric current. Consider what happens when a clean piece of copper metal is placed in a solution of silver nitrate (Figure 1). As soon as the copper metal contacts the solution, silver metal begins to form on the copper surface and copper ions pass into the solution. The blue-green color of the solution on the far right of Figure 1 indicates the presence of copper ions. Thus the net ionic equation for the reaction is
Cu(s) + 2 Ag+(aq) → Cu2+(aq) + 2 Ag(s)

The redox reaction may be split into its two half-reactions that sum to the overall reaction:
Reduction: 2 Ag+(aq) + 2 e¯ ⟶ 2Ag(s)
The half-reactions make clear that two electrons are transferred from a copper atom to form a copper(II) ion. Each of the two electrons is transferred to one silver(I) ion to form a silver atom. Because a flow of electrons constitutes an electric current, this electron transfer could generate an electric current if we could devise a way to carry out one half-reaction in one place and connect it with a wire to the other half-reaction in a different place. This is how a voltaic cell is designed. Figure 2 shows one way to do this.
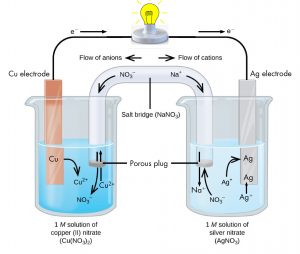
The beaker on the left contains a 1-M solution of copper(II) nitrate [Cu(NO3)2] with a strip of copper metal partially submerged in the solution. The copper is an electrode, a means for conducting electrons into or out of the solution. At the surface of the copper strip copper atoms lose electrons to form copper(II) ions that go into solution. The electrons are conducted out of the solution by the copper strip and move through the wire. Notice that copper, copper(II) ions, and electrons are in the first half-reaction above: the oxidation half-reaction. The flow of electrons (electric current) passes through the light bulb and moves are toward the silver strip in the beaker on the right. In the right-hand beaker silver(I) ions near the surface of the silver strip gain electrons and form silver atoms, which attach to other silver atoms in the silver strip. Notice that silver(I) ions, electrons, and silver metal are in the second half-reaction above: the reduction half-reaction. Thus, with the two half-reactions in separate beakers, an electric current can be generated. The container in which each half-reactions occurs is called a half-cell.
If this were all that happened, the electric current could not flow for long. In the left-hand beaker one copper(II) ion is added to the solution for every two electrons conducted into the external wire. This means that the solution in the beaker has more positive ions than negative ions and an electric charge would build up on the solution unless either some positive ions move out of the beaker or some negative ions move into the beaker. A similar issue arises in the right-hand beaker, where silver(I) ions are being removed from the solution. Balancing total ionic charges requires either that negative ions move out of the right-hand solution or positive ions move in. This balancing of ion charges in the beaker is maintained by the salt bridge, a solution of a salt that does not mix with either half-cell solution but allows ions to pass into or out of the half-cells. By allowing ions to conduct charge into or out of the half-cells, the salt bridge completes the electrical circuit involving the two half-cells. Without it no current can flow and the bulb cannot light. Notice that if the salt bridge is considered part of an electrical circuit, negative ions in the salt bridge more in the same direction as electrons around the circuit and positive ions move in the opposite direction.
The half-cell in which oxidation occurs is called the anode. The half-cell in which reduction occurs is called the cathode. It is easy to remember that the anode involves oxidation because both words begin with vowels. It is easy to remember that the cathode involves reduction because both words begin with consonants. These definitions, anode/oxidation and cathode/reduction, are true for any electrochemical cell, not just a voltaic cell.
Exercise 4: Electric Energy and Flow of Charge
You light a 25-W light bulb with the current from a 12-V lead-acid battery. (Assume 100% efficiency.)
Calculate how much energy the light bulb uses after 1.0 hour of operation.
Calculate how many coulombs passed through the light bulb during that time.
Podia Question
Make a diagram of a voltaic cell that generates electric current from this product-favored chemical reaction:
Fe(s) + Cu(NO3)2(aq) → Fe(NO3)2(aq) + Cu(s)
Choose an appropriate salt solution for the salt bridge. Make sure that the oxidation half-reaction is in the left-hand beaker. Label each electrode with an element symbol. Label the anode half-cell and the cathode half-cell. Label the direction of movement of electrons, positive ions, and negative ions in the electrical circuit.
As this voltaic cell operates, one electrode gains mass and one electrode loses mass. Identify which electrode gains mass. Explain why that electrode gains mass and why the other electrode loses mass.
Two days before the next whole-class session, this Podia question will become live on Podia, where you can submit your answer.

