As you work through this section, if you find that you need a bit more background material to help you understand the topics at hand, you can consult “Chemistry: The Molecular Science” (5th ed. Moore and Stanitski) Sections 5-7 and 5-8, and/or Chapter 3.1-3.5 in the Additional Reading Materials section.

D4.1 Atoms with More than a Single Electron

When there are two or more electrons in an atom, the ideas about quantum numbers, orbitals, and shapes of electron-density distributions that we developed for a hydrogen atom remain useful. However, the energy depends on electron-electron repulsions as well as electron-nucleus attractions. For example, in a helium atom the energy is lowered because of attraction between each electron and the 2+ charge of the nucleus, but it is raised by repulsion between the two electrons. Based on Coulomb’s law and assuming the same distance between nucleus and electron density distribution, you might expect the energy of an electron in a helium atom to be twice as low as for a hydrogen atom [because Q₁Q₂ is now (+2)(−1) instead of (+1)(−1)]; however, electron-electron repulsions raise this energy significantly and a helium atom is not as stable as we might have expected.

For atoms with many electrons, the effect of electron-electron repulsions differs for different subshells. Therefore subshells with the same n value have different energies and the energy depends on both n and ℓ quantum numbers. As ℓ increases the energy also increases, so s-subshell electrons have lower energy than p-subshell electrons, which are lower than d-subshell electrons, and so forth. Orbitals within the same subshell (for example 2p, or 3d) all have the same energy; orbitals that have the same energy are said to be degenerate. As orbital energies increase this difference between s, p, d, and f subshells results in electrons with different n values having similar energies. An example is the 3d and 4s subshell energies shown in Figure 1.

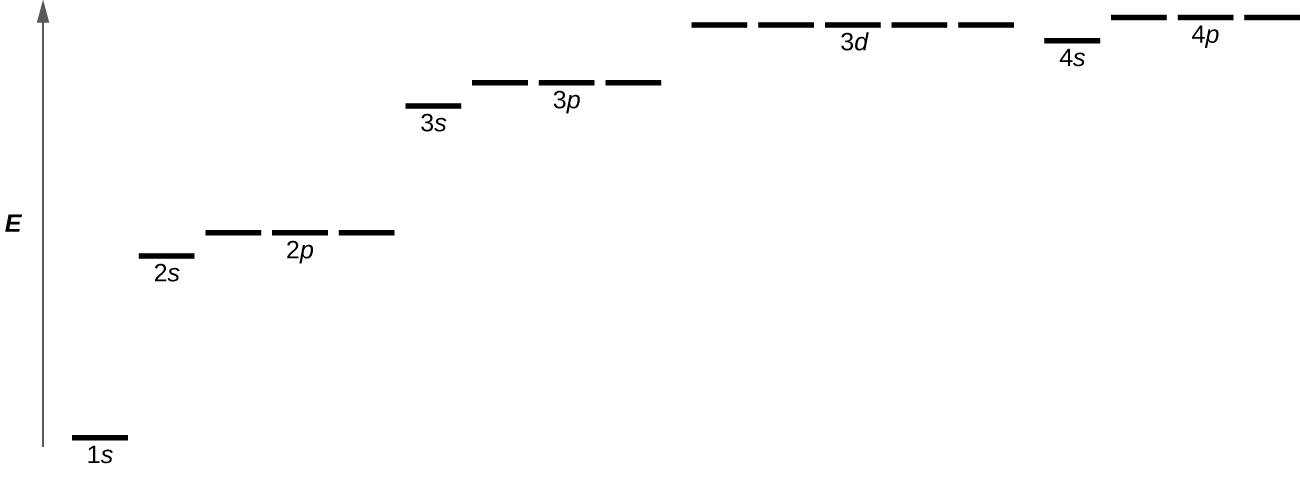
The Austrian physicist Wolfgang Pauli formulated what is now called the Pauli exclusion principle: each electron in an atom must have a different set of values for the four quantum numbers. That is, if two electrons share the same orbital (have the same set of quantum numbers n, ℓ, and m_ℓ), then their spin quantum numbers m_s must have different values (the electrons must have opposite spins). Because the spin quantum number can only have two values [latex](m_s = \pm \frac{1}{2})[/latex], no more than two electrons can occupy the same orbital. The arrangement of electrons (and hence the electron-density distribution) in any multi-electron atom can be determined by recognizing that the ground state of an atom has electrons in orbitals that result in the lowest possible energy and applying the Pauli principle.

D4.2 Electron Configurations

The specific arrangement of electrons in the shells, subshells, and orbitals of an atom is called the electron configuration of the atom. The electron configuration determines many physical and chemical properties of that atom. An electron configuration is written symbolically to provide three pieces of information: the principal quantum number (shell number), n; a letter that designates the subshell (the orbital type: s, p, d, or f); a superscript number that designates the number of electrons in that particular subshell. For example, the notation 2p⁴ indicates 4 electrons in a p subshell (ℓ = 1) with a principal quantum number (n) of 2.

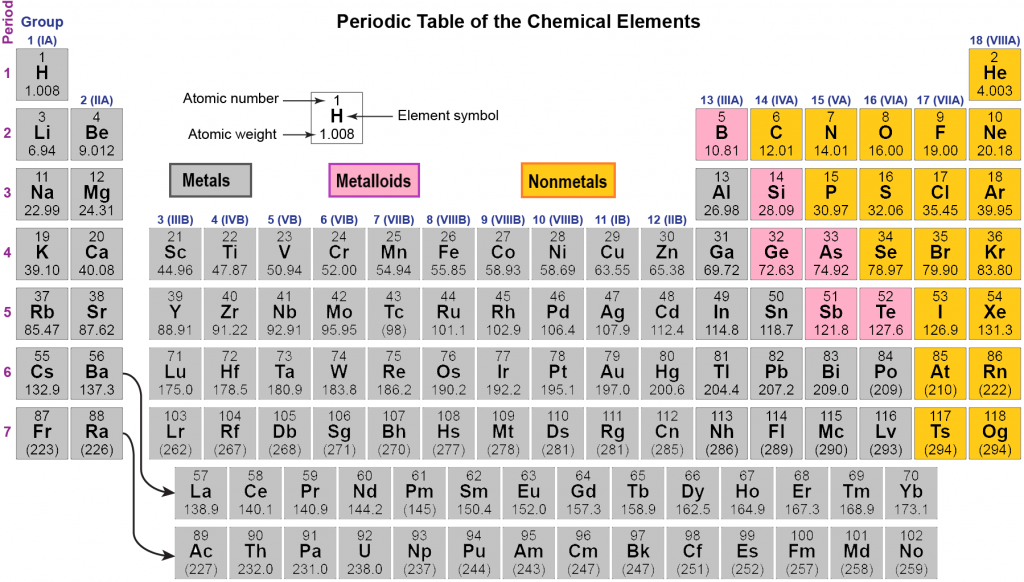
The structure of the periodic table is determined by the chemical behavior of the elements, which in turn depends on the electron configurations of the atoms; therefore, the periodic table can be used to predict electron configurations. For any specific atom, the electron configuration can be built up by starting with hydrogen and following the elements in atomic-number order through the periodic table. To go from one atom to the next, add one proton (and one or more neutrons) to the nucleus and one electron to the lowest-energy subshell that has at least one orbital with fewer than two electrons. Repeat until you reach the desired element. This procedure is called the Aufbau principle, from the German word Aufbau (“to build up”). Click on Figure 1 to see how to use the building-up process to determine the electron configurations of oxygen, O, and chromium, Cr.

Figure 1. For each element, this periodic table shows the number of electrons  in the highest-energy subshell. By “building up” from hydrogen, you can use the periodic table to determine the electron configuration for any atom. Click on the table to see how the building-up process works.

The colored sections of Figure 1 classify the elements based on the orbital designation of the last electron added to an atom in the building-up process. For an s-block element the last electron added is in an s orbital, and so forth. These colored sections also delineate groups of elements that chemists refer to by specific names:

1. Main group elements (also called representative elements) are those in the s-block or p-block, shown in blue and peach in Figure 1. This category includes all the nonmetallic elements, some metals, and the intermediate semimetallic elements.
2. Transition elements (also called transition metals) are d-block elements, shown in yellow in Figure 1. All d-block elements are metals, hence the name transition metals.
3. Inner transition elements are f-block elements, shown in green in Figure 1. All are metals. Often the first green row in Figure 1 is called the lanthanide series and the second green row the actinide series.

Writing the complete electron configuration for an atom with a large atomic number takes a lot of space, so chemists often abbreviate configurations by using the noble-gas notation. For example, the electron configuration of V is 1s²2s²2p⁶3s²3p⁶4s²3d³. The noble gas that precedes V in the building-up process is Ar; its electron configuration is 1s²2s²2p⁶3s²3p⁶ so we can replace this part of the Ti configuration with [Ar]. Thus the configuration of V is shortened to [Ar]4s²3d³. A list of ground-state electron configurations for all elements is in an appendix; the list uses noble-gas notation.

D4.3 Orbital diagrams

Because of electron spin, each electron behaves as a tiny magnet. Two electrons with parallel (same-direction) spins produce greater magnetic field than just one. To predict magnetic properties, it is useful to know how electrons are distributed among orbitals within a subshell. An orbital diagram provides this kind of detail, showing individual orbitals as boxes and using arrows to designate spin direction of electrons. For example, an uncharged boron atom has a ground state electron configuration of 1s²2s²2p¹. The up and down arrows represent the [latex]m_s = + \frac{1}{2}[/latex] or [latex]m_s = - \frac{1}{2}[/latex] spins of electrons.

An orbital diagram includes boxes for all orbitals in a subshell, even if some orbitals are unoccupied. The three 2p orbitals are degenerate so the electron can occupy any one of them.

In a carbon atom, electron configuration 1s²2s²2p², there are two electrons in the three degenerate 2p orbitals. We could pair the electrons in one of the 2p orbitals; we could put electrons in two separate orbitals, but with opposite spin; or the electrons could have parallel spins in two different 2p orbitals. According to  Hund’s rule, the lowest-energy configuration has the maximum number of unpaired electrons within a set of degenerate orbitals. Thus, the orbital diagram for the ground state of carbon is

D4.4 Valence Electrons and Lewis Diagrams

Valence refers to the capacity of an atom to combine with other atoms. For example, the valence of O is 2 and the valence of Na is 1; thus, it takes two Na atoms to combine with one O atom and the formula for sodium oxide is Na₂O. When two atoms approach and form a chemical bond, the electron density distributions that extend farthest from the nucleus of each atom determine valence because these are the first electrons to contact and interact with electrons in the other atom. Electrons occupying the outermost orbitals of an atom are called valence electrons; electrons occupying inner orbitals, with electron density closer to the nucleus, are called core electrons.

When an electron configuration is written using the noble-gas notation, all electrons represented by a noble-gas symbol in brackets are core electrons. Electrons beyond the noble-gas configuration are valence electrons if they are in the outermost shell of the atom (have the highest n value for the atom) or if they are in incompletely filled subshells. For example, consider the element vanadium, V: [Ar]4s²3d³. There are five valence electrons: two 4s electrons (in the outermost shell, n = 4) and three 3d electrons (in an incompletely-filled subshell). There are 18 core electrons in the 1s, 2s, 2p, 3s, and 3p subshells. The fact that V has five valence electrons results in V forming compounds in which the valence of vanadium ranges from 2 to 5.

The idea that valence electrons determine chemical properties of elements came from the American chemist Gilbert N. Lewis. Lewis also suggested a simple way to keep track of the number of valence electrons: draw dots around the symbol of an element to represent the valence electrons. The element symbol then represents the nucleus and core electrons of an atom. This notation is called a Lewis diagram. Lewis diagrams are most often used for the main-group (representative) elements. Here are Lewis diagrams for atoms of elements in the third row of the periodic table:

When drawing a Lewis diagram dots are added one at a time to each of the four sides of the element symbol. If there are more than four dots to add, dots are paired. Lewis originated the idea that when an atom bonds to another atom the valence electrons rearrange to form an octet, a stable configuration of valence electrons (s²p⁶) that corresponds to each noble gas at the right side of a row in the periodic table. Thus Lewis diagrams for atoms can predict how an atom forms chemical bonds, an idea that we will explore later.

D4.5 Metals

Knowledge about valence electrons can help us understand properties of metals, which include most of the elements in the periodic table (Figure 2). All solid and liquid metals conduct heat and electricity well, have lustrous (metallic-looking) surfaces, and are malleable (deform, rather than shatter, when hammered). Many are hard and quite strong and are useful construction materials. Most metals have melting points far above room temperature; for example, most transition metals melt above 1000 °C. Exceptions are mercury, which is a liquid, and metals in periodic group 1 (IA), which melt below 200 °C, and a few other metals with low melting points.

In a metallic solid the atoms are packed closely (Figure 3) and valence electrons can be shared among many different atoms. With only its nucleus and core electrons, a metal atom would be positively charged, so the negatively charged valence electrons attract the the positive metal-atom cores. This attraction is known as metallic bonding. Because the valence electrons can move easily, if an atom moves relative to other atoms, the valence electron-atomic core attraction is easily re-established; that is metallic bonding is not specific to a particular direction.

D4.6 Electron Configurations of Monoatomic Ions

A monoatomic ion is a single atom that has gained or lost one or more electrons. A cation, a positively charged ion, forms when an atom loses one or more electrons. An anion, a negatively charged ion, forms when an atom gains one or more electrons. To find the electron configuration of a monoatomic ion, start with the electron configuration of the corresponding atom and remove (or add) an appropriate number of electrons from (or to) the valence orbitals of the atom.

Atoms of elements on the far right side of the periodic table (except the noble gases) usually gain electrons and form anions. These atoms correspond to elements that are non-metals. Atoms on the left side of the periodic table, including transition and inner-transition elements, usually lose electrons and form cations. These are atoms of elements that are metals.

Among main-group elements, atoms of elements in periodic groups IA, IIA, and IIIA lose 1, 2, or 3 electrons to form the electron configuration of a noble gas (an octet, s²p⁶), or a noble gas plus filled inner d and f subshells. Atoms of elements in periodic groups VIIA, VIA, and some in VA gain 1, 2, or 3 electrons. Here are examples that show electron configurations and Lewis diagrams:

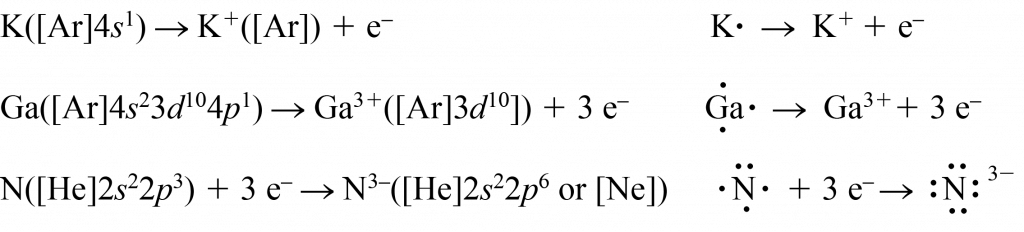
When atoms of transition elements and inner transition elements lose electrons to form cations, electrons in the outermost shell (that is, electrons in an s orbital) are lost before any d or f electrons are lost. This happens because the cation formed is more stable (lower in energy) if it contains only electrons in inner shells. Removal of one or more electrons reduces overall electron repulsions, thereby reducing the total energy. The energy reduction is greater for inner-shell electrons, which are closer to other electrons. Thus, when transition elements lose electrons to form ions, the ions contain only d electrons; both s electrons are lost. Except for scandium, every transition element in the fourth period forms a 2+ ion (by losing its two 4s electrons). Most of these transition elements can also lose one or more 3d electrons to form 3+ and higher-charged ions. Similarly, atoms of inner transition elements initially lose s electrons; if 3+ or higher-charged ions form, then f electrons are lost. Here are some examples:

Cr ([Ar]4s²3d⁴)  →  Cr²⁺ ([Ar]3d⁴)  +  2 e⁻

Cr ([Ar]4s²3d⁴)  →  Cr³⁺ ([Ar]3d³)  +  3 e⁻

Eu ([Xe]6s²4f⁷)  →  Eu²⁺ ( ([Xe]4f⁷)  + 2 e⁻

Eu ([Xe]6s²4f⁷)  →  Eu³⁺ ( ([Xe]4f⁶)  + 3 e⁻

Ions and atoms that have the same electron configuration are isoelectronic. For example, Na⁺, Ne, and F⁻ all have electron configuration 1s²2s²2p⁶ (or [Ne]) so Na⁺, Ne, and F⁻ are isoelectronic. For main-group elements, the most stable ions are isoelectronic with a noble gas; that is, the most stable ions have complete octets.

D4.7 Unpaired Electrons and Magnetism

You are probably familiar with refrigerator magnets, iron magnets, or neodymium (rare earth) magnets. These exhibit ferromagnetism, a strong attraction to a magnetic field that is easily observable and sometimes can be made permanent. All substances exhibit diamagnetism, very weak repulsion from a magnetic field that can only be observed in extremely large magnetic fields. (Click here to see videos of a water droplet and a live frog levitated by repulsion from a very strong magnetic field.) Because diamagnetism is so weak, it is usually too small to notice.

Some substances exhibit paramagnetism, attraction to a magnetic field that is not as strong as ferromagnetism but much stronger than diamagnetism. Paramagnetism arises because of unpaired electrons. Each electron spin creates a tiny magnetic field. When a magnet comes near a paramagnetic substance, most of the electron spins align with the magnetic field, causing the substance to be attracted to the magnet. This is shown in Figure 4. Figure 5 shows how ferromagnetism differs from paramagnetism.

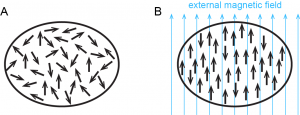
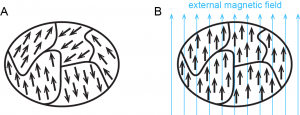
When electrons are paired, their opposite spins create opposite magnetic fields that cancel each other; substances with all electrons paired are neither paramagnetic nor ferromagnetic, so we refer to them as diamagnetic. Paramagnetic and diamagnetic materials do not act as permanent magnets. A magnetic field is required to make them magnetic. The magnitude of paramagnetism can be measured by weighing a sample with a highly sensitive balance and then weighing it again with a strong magnet just below the sample. A sample that is attracted to the magnet appears heavier because the magnet attracts it downward. The increase in apparent weight is proportional to the number of unpaired electrons.