Unit Four

Day 40: Thermodynamic Properties of Electrochemical Cells

As you work through this section, if you find that you need a bit more background material to help you understand the topics at hand, you can consult “Chemistry: The Molecular Science” (5th ed. Moore and Stanitski) Chapter 17-6 and 17-7, and/or Chapter 17.6-17.7 in the Additional Reading Materials section.

D40.1 Relationships among ΔrG°, K°, and E°cell

Like any chemical reaction, a redox reaction can be described in terms of ΔrG° (standard Gibbs free energy change) and K° (standard equilibrium constant). These thermodynamic variables can be related to E°cell, because they all tell us whether the redox reaction is reactant-favored or product-favored.

In a voltaic cell, the difference in Gibbs free energy between products and reactants can do electrical work. We represent electrical work done by the cell by welec.

welec (J) = charge transferred (C) × potential difference (V)

The charge of 1 mol electrons is known as the Faraday’s constant (F):

[latex]F = \dfrac{6.0221\;\times\;10^{23}\;\text{e}^{-}}{\text{mol}}\;\times\;\dfrac{1.6022\;\times\;10^{-19}\;\text{C}}{\text{e}^{-}} = 96485\;\frac{\text{C}}{\text{mol}} = 96485\frac{\text{J}}{\text{V}{\cdot}\text{mol}}[/latex]

Hence, the total quantity of charge transferred per mole of a redox reaction is:

total charge per mole of reaction = number e¯ transferred × F = n × F

In this equation n is the number of electrons transferred in the balanced redox reaction. This number of electrons can be obtained from the half-reactions that are added to produce the overall redox reaction. For example, in the reaction

2 Au3+(aq)  +  3 Zn(s)  →  3 Zn2+(aq)  +  2 Au(s)

6 e− are transferred because each half-reaction, after multiplying by a factor to balance electrons, involves 6 e−:

Oxidation:     3 Zn(s)  →  3 Zn2+(aq)  + 6 e−
Reduction:     2 Au3+(aq)  + 6 e−  →  2 Au(s)

(Verify that these half-reactions sum to the overall reaction.) When this reaction equation happens once, 6 e− are transferred. When a mole of reaction takes place 6 mol e− is transferred; that is, 6 mol × 96485 C/mol = 578910 C is transferred.

Multiplying the charge transferred by the cell potential gives welec = (nF)(Ecell) = nFEcell.

It is possible to operate a voltaic cell so that the maximum possible electrical work, welec, is done and the only work done is electrical work. For a cell operating under such conditions, ΔrG = −wmax = −welec. (The relation ΔrG = −wmax was derived in Section D32.1.) Thus,

ΔrG = −wmax = −welec =  −nFEcell

The negative sign makes sense because a positive Ecell indicates a spontaneous reaction and a negative ΔrG also indicates a spontaneous reaction.

If all the reactants and products are in their standard states, the preceding equation becomes:

ΔrG°  = –nFE°cell

This equation provides a way to relate standard cell potentials to equilibrium constants, since:

ΔrG° = –RTlnK° = –nFE°cell

Therefore:

–nFE°cell = –RTlnK°     or     [latex]E_{\text{cell}}^{\circ} = \dfrac{RT}{nF}\;\text{ln}\;K^{\circ}[/latex]

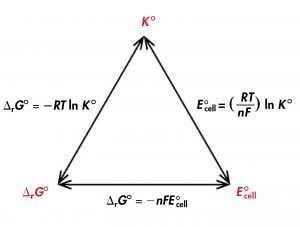
Thus, if ΔrG°, K°, or E°cell is known or can be calculated, the other two quantities can be determined using the relationships in Figure 1. Moreover, any of the three quantities can be used to determine whether a reaction is product-favored.

A diagram is shown that involves three double headed arrows positioned in the shape of an equilateral triangle. The vertices are labeled in red. The top vertex is labeled “K standard.“ The vertex at the lower left is labeled “delta G standard” The vertex at the lower right is labeled “E standard subscript cell.” The right side of the triangle is labeled “E superscript degree symbol subscript cell equals ( R T divided by n F ) l n K superscript degree symbol.” The lower side of the triangle is labeled “delta G superscript degree symbol equals negative n F E superscript degree symbol subscript cell.” The left side of the triangle is labeled “delta G superscript degree symbol equals negative R T l n K superscript degree symbol.”
Figure 1. The relationships among ΔrG°, K°, and E°cell.

Example 1

Equilibrium Constants, Standard Cell Potentials, and Standard Gibbs Free Energy Changes
Determine the standard Gibbs free energy change and equilibrium constant for this reaction at 25 °C.

[latex]2\text{Ag}^{+}(aq)\;+\;\text{Fe}(s)\;{\leftrightharpoons}\;2\text{Ag}(s)\;+\;\text{Fe}^{2+}(aq)[/latex]

Solution
The reaction involves an oxidation-reduction reaction, so the standard cell potential can be calculated using data from the appendix: [latex]E_{\text{Fe}^{2+}/\text{Fe}}^{\circ} = -0.44\;\text{V}[/latex] and [latex]E_{\text{Ag}^{+}/\text{Ag}}^{\circ} = 0.7991;\text{V}[/latex] for the half reactions:

[latex]\begin{array}{lrcll} \text{anode (oxidation):} & \text{Fe}(s) &\longrightarrow& \text{Fe}^{2+}(aq)\;+\;2\text{e}^{-} \\[0.5em] \text{cathode (reduction):} & 2\;\times\;(\text{Ag}^{+}(aq)\;+\;\text{e}^{-} &\longrightarrow& \text{Ag}(s)) \end{array}[/latex]
[latex]E_{\text{cell}}^{\circ} = E_{\text{cathode}}^{\circ}\;-\;E_{\text{anode}}^{\circ} = E_{\text{Ag}^{+}/\text{Ag}}^{\circ}\;-\;E_{\text{Fe}^{2+}/\text{Fe}}^{\circ} = +1.24\;\text{V}[/latex]

From the half-reactions, n = 2, so the equilibrium constant is:

[latex]E_{\text{cell}}^{\circ} = \dfrac{RT}{nF}\;\text{ln}\;K^{\circ}\;\;\;\;\;\text{or}\;\;\;\;\;\text{ln}\;K^{\circ} = \dfrac{nFE_{\text{cell}}^{\circ}}{RT}[/latex]
[latex]\begin{array}{rcl}\text{ln}\;K^{\circ} &=& \frac{(2)(96485\;\text{J}/\text{V}{\cdot}\text{mol})(1.24\;\text{V})}{(8.314\;\text{J}/\text{K}{\cdot}\text{mol})(298\;\text{K})} \\[0.5em] \text{ln}\;K^{\circ} &=& 96.6 \\[0.5em] K^{\circ} &=& e^{96.6} = 9\;\times\;10^{41} \end{array}[/latex]

The standard Gibbs free energy change is:

[latex]{\Delta}G^{\circ} = -nFE_{\text{cell}}^{\circ}[/latex]
[latex]{\Delta}G^{\circ} = -2\;\times\;96485\;\frac{\text{J}}{\text{V}{\cdot}\text{mol}}\;\times\;1.24\;\text{V} = -239\;\frac{\text{kJ}}{\text{mol}}[/latex]

Check your answer: A positive standard cell potential means a product-favored reaction, so the standard Gibbs free energy change should be negative, and the equilibrium constant should be >1.

Check Your Learning
Calculate the standard Gibbs free energy change and the equilibrium constant for this reaction at room temperature. Is the reaction product-favored?

[latex]\text{Sn}(\text{s})\;+\;2\;\text{Cu}^{2+}(\text{aq})\;{\leftrightharpoons}\;\text{Sn}^{2+}(\text{aq})\;+\;2\;\text{Cu}^{+}(\text{aq})[/latex]

Answer:

n = 2; [latex]E_{\text{cell}}^{\circ} = +0.297\;\text{V;}\;{\Delta}G^{\circ} = -57.3\;\frac{\text{kJ}}{\text{mol}}[/latex]; K° = 1 × 1010.

The reaction is product-favored.

Exercise 1: Standard Half-Cell Potentials and Standard Gibbs Free Energy Change

Answer the questions below regarding this reaction. (See appendix for standard potential values.)

2 Zn(s) + O2(g) + 2 H2O(l) → 2 Zn2+(aq) + 4 OH–(aq)

D40.2 Nernst Equation

Now that the connection has been made between standard Gibbs free energy change and standard cell potentials, we can consider the situation under nonstandard conditions. Recall that:

ΔrG = ΔrG° + RT lnQ

Converting to cell potentials:

–nFEcell = –nFE°cell + RTlnQ     or     [latex]E_{\text{cell}} = E_{\text{cell}}^{\circ}\;-\;\dfrac{RT}{nF}\;\text{ln}\;Q[/latex]

The equation on the right is the Nernst equation. The Nernst equation can be used to calculate the cell potential at  concentrations or partial pressures that differ from standard conditions.

Example 2

Cell Potentials at Nonstandard Conditions
Consider this reaction at room temperature:

[latex]\text{Co}(\text{s})\;+\;\text{Fe}^{2+}(\text{aq},\;1.94\;\text{M})\;{\longrightarrow}\;\text{Co}^{2+}(\text{aq},\;0.15\;\text{M})\;+\;\text{Fe}(\text{s})[/latex]

Is the process spontaneous in the forward direction?

Solution
There are two ways to solve the problem: (1) If thermodynamic data are available, you could calculate the Gibbs free energy change. If the Gibbs free energy change is negative, the process is spontaneous. (2) If standard half-cell potential data are available, you could calculate the cell potential. If the cell potential is positive, the process is spontaneous.

We use approach (2).  We first calculate the standard cell potential. The half reactions are listed below, with standard half-cell potentials of [latex]E_{\text{Co}^{2+}/\text{Co}}^{\circ} = -0.277\;\text{V}[/latex] and [latex]E_{\text{Fe}^{2+}/\text{Fe}}^{\circ} = -0.44\;\text{V}[/latex]:

[latex]\begin{array}{lrcll} \text{Anode (oxidation):} & \text{Co}(\text{s}) &\longrightarrow& \text{Co}^{2+}(\text{aq})\;+\;2\;\text{e}^{-} \\[0.5em] \text{Cathode (reduction):} & \text{Fe}^{2+}(\text{aq})\;+\;2\;\text{e}^{-} &\longrightarrow& \text{Fe}(\text{s}) \end{array}[/latex]
[latex]E_{\text{cell}}^{\circ} = E_{\text{cathode}}^{\circ}\;-\;E_{\text{anode}}^{\circ} = -0.44\;\text{V}\;-\;(-0.277\;\text{V}) = -0.16\;\text{V}[/latex]

The process is not product-favored under standard conditions.

Using the Nernst equation, given the concentrations stated in the problem and n = 2:

[latex]Q = \dfrac{[\text{Co}^{2+}]}{[\text{Fe}^{2+}]} = \dfrac{0.15\;M}{1.94\;M} = 0.077[/latex]
[latex]\begin{array}{rcl} E_{\text{cell}} &=& E_{\text{cell}}^{\circ}\;-\;\frac{RT}{nF}\;\text{ln}\;Q \\[0.5em] &=& -0.16\;\text{V}\;-\;\dfrac{(8.314\;\text{J}/\text{K}{\cdot}\text{mol})(298\;\text{K})}{(2)(96485\;\text{J}/\text{V}{\cdot}\text{mol})}\;\text{ln}(0.077) \\[0.5em] &=& -0.16\;\text{V}\;+\;0.033\;\text{V} = -0.13\;\text{V}\end{array}[/latex]

The process is nonspontaneous under the given conditions.

Check Your Learning
Calculate the cell potential for this reaction at room temperature.

[latex]\text{Al}(\text{s}){\mid}\text{Al}^{3+}(\text{aq},\;0.15\;\text{M}){\parallel}\text{Cu}^{2+}(\text{aq},\;0.025\;\text{M}){\mid}\text{Cu}(\text{s})[/latex]

Determine the values of n and Q for the overall reaction Is the reaction spontaneous under these conditions?

Answer:

n = 6; Q = 1440; Ecell = +1.98 V, spontaneous.

Podia Question

The gravity cell, a variant of the Daniell cell, was described in Exercise 2, Section D39.2. The cell involves oxidation of Zn(s) by Cu2+(aq). Suppose a gravity cell is constructed with 1.00 L saturated copper(II) sulfate in the bottom and 1.00 L 0.100-M zinc sulfate in the top. (There is no solid copper(II) sulfate in the cell. Assume a temperature of 25 °C.)

Write half-reactions for the overall reaction that powers the gravity cell and label them as oxidation and reduction.

Write the balanced overall cell reaction.

Calculate the standard cell potential.

Calculate the cell potential under the initial (nonstandard) conditions. The solubility of CuSO4•5H2O in water is 32 g/100 mL.

Calculate the cell potential after 99% of the copper(II) ions in the bottom cell solution has reacted. (Assume there is an excess of Zn(s).)

Two days before the next whole-class session, this Podia question will become live on Podia, where you can submit your answer.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chemistry 109 Copyright © by John Moore; Jia Zhou; and Etienne Garand is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.