Unit One
Day 5: Periodic Trends and Ionic Compounds
As you work through this section, if you find that you need a bit more background material to help you understand the topics at hand, you can consult “Chemistry: The Molecular Science” (5th ed. Moore and Stanitski) Sections 5-9 through 5-13, Sections 2-4 through 2-6, and Section 9-7, and/or Chapter 3.6-3.13 in the Additional Reading Materials section.
D5.1 Electron Configurations and Periodic Trends
The rules governing quantum numbers together with the relative energies of subshells give rise to electron configurations that repeat periodically. For example, each noble gas has a configuration s2p6, an octet, that results in low chemical reactivity. Each element that follows a noble gas in the building-up process has a single valence electron that is easily removed; elements in periodic group 1 (or IA) are highly reactive, easily forming positive ions. These periodic repetitions of electron configurations are the basis for the periodic table: elements with similar atomic electron configurations are in vertical columns in the periodic table. Their similar configurations result in similar chemical properties. In particular, elements in vertical columns in the table form compounds with similar formulas. For example, all elements in group 1 form chlorides, bromides, and iodides with formulas MCl, MBr, and MI, where M represents H, Li, Na, K, Rb, Cs, or Fr.
Electron configurations are related to a number of atomic properties as well as chemical formulas. Periodic trends in these atomic properties can be predicted by applying ideas about attraction of electrons to atomic nuclei and of repulsions among electrons:
- Electron-density distributions are in shells that increase in size as the principal quantum number, n, increases; electrons in larger shells are, on average, farther from the nucleus and less strongly attracted.
- Electrons repel other electrons, raising electrostatic potential energy. This partly counteracts the lowering of energy due to attraction of an electron by the nucleus. Electrons are said are said to screen or shield other electrons from nuclear charge.
Exercise 1: Electrostatic Attraction and Repulsion
Especially important is that electron density in inner shells mostly is closer to the nucleus than electron density in outer shells. Thus, electrons in the inner shells significantly counteract the effect of nuclear attraction. Consider a lithium atom, which has three protons in the nucleus and three electrons surrounding the nucleus. The electron configuration is 1s22s1. Because the 2s orbital is much larger than the 1s orbital, the 1s electron density is between the nucleus and the 2s electron much of the time. Thus, the two 1s electrons repel the 2s electron away from the nucleus, counteracting part of the 3+ charge of the three protons in the nucleus. (Move the slider at the bottom of Figure 1 halfway across to see how much of the 1s electron density lies between the nucleus and 2s electron density.)
To account for repulsion of electrons in outer shells by electrons in inner shells, we say that the effective nuclear charge is less than the actual nuclear charge because of electron repulsions. For a specific electron, effective nuclear charge is the positive nuclear charge (given by the atomic number) reduced by the repulsion of the electron by all the other electrons. In the case of the 2s electron in the lithium atom in the figure, the repulsion between the two 1s electrons and the 2s electron reduces nuclear charge by 1.72; that is, the effective nuclear charge for the 2s electron is 3 − 1.72 = 1.28. Had all the electron density of the 1s electrons been between the nucleus and the 2s electron, the nuclear charge would have been reduced by two units, to 1.
D5.2 Periodic Variation of Atomic Radius
It is often useful to think of atoms as if they were tiny spheres with nuclei at their centers. Then the size of an atom can be defined by the radius of a sphere. One way to determine atomic radii is to measure the distance between the nuclei of two atoms of the same element that are bonded to each other; the radius is half the internuclear distance. A second way is to measure the distance between the nuclei of two atoms in a solid metal, where each atom touches several nearest neighbors. Once a set of atomic radii has been determined, the radii can be used to predict the lengths of bonds that have not yet been measured. A table of atomic radii is in the appendix.
Here are three correct statements about the data in Figure 2. In your notebook write a clear, concise explanation for why each statement is true. It may help to review the discussion in section D5.1.
- There is a large increase in atomic radius going from a noble-gas element to the following group 1A element.
- Within each period, such as the elements from Na to Ar, atomic radius decreases as atomic number increases.
- Within a periodic group, such as group 1 (H, Li, Na, K, Rb, Cs, Fr), atomic radius increases going down the periodic table.
Exercise 2: Predicting Atomic Radii
D5.3 Periodic Variation of Ionic Radii
Ionic radius is the radius of a sphere that represents a positive or negative ion. (There is an ionic radius table in an appendix.)
A cation has fewer electrons and the same number of protons as the parent atom; there are fewer electron-electron repulsions but the same nuclear attraction, so cations are smaller than the atoms from which they are derived. For example, the atomic radius of Al (1s22s22p63s23p1) is 143 pm, whereas the ionic radius of Al3+ (1s22s22p6), with only core electrons remaining, is 68 pm. Cations with higher positive charges are smaller than cations with lower charges; for example, V2+ has an ionic radius of 93 pm, while that of V3+ is 78 pm. Proceeding down the groups of the periodic table, we find that cations of successive elements with the same charge generally have larger radii, corresponding to an increase in the principal quantum number, n.
An anion is formed by adding one or more electrons to the valence shell of an atom. There is greater repulsion among the electrons and a decrease in effective nuclear charge for the outermost electrons. This causes anion radii to be larger than for the parent atom. For example, the atomic radius of S ([Ne]3s23p4) is 104 pm, whereas the ionic radius of S2- ([Ne]3s23p6) is 170 pm. Going down any periodic group row by row, anions of the same charge have larger principal quantum numbers and, thus, larger radii.
Earlier we defined atoms and ions that have the same electron configuration as isoelectronic. An example of isoelectronic species are N3–, O2–, F–, Ne, Na+, Mg2+, and Al3+ (all 1s22s22p6). For isoelectronic atoms or ions, the greater the nuclear charge (number of protons), the smaller the ionic radius. This implies that isoelectronic anions are larger than cations. Indeed, anions are usually larger than cations even if they are not isoelectronic.
Exercise 3: Atomic and Ionic Radii
Rank these atoms/ions from smallest to largest radii.
K K+ Ar– Ar
D5.4 Periodic Variation of Ionization Energies
The quantity of energy required to remove an electron from an atom is called ionization energy. Because most atoms contain more than a single electron, there are successive ionization energies: the first ionization energy is for removing the least tightly bound electron; the second ionization energy is for removing an electron from a 1+ cation (the second easiest electron to remove); the third ionization energy is for removing a third electron and so forth. The first ionization energy, IE1, corresponds to this equation,
and the second ionization energy, IE2, to this one,
Energy is always required to remove electrons from atoms or ions, so ionization is endothermic and IE values are always positive.
The least tightly held electron is easier to remove because it is located farther from the nucleus. Based on what you have just learned about atomic radii, predict how first ionization energy varies
- from one atom to the next going across the periodic table
- from one atom to the next going down a periodic group
In Activity 5 you developed a general rule that across a period, IE1 increases with increasing atomic number, Z; down a group, IE1 decreases with increasing Z. There are some systematic deviations from this trend, four of which occur in periods 1, 2, and 3. Look at Figure 3 again, locate the deviations in the first three periods, and click on each one.
In your notebook, write an explanation for the fact that IE1 for B is smaller than IE1 for Be. (It may help to write the electron configuration for each atom.)
Another deviation from the trend of increasing IE across a period occurs when a subshell becomes more than half filled. The first ionization energy for oxygen is slightly less than that for nitrogen. The orbital box diagram of oxygen shows that the last electron added is forced to pair because the p subshell is more than half full. Loss of one electron reduces electron–electron repulsion because there are no longer two electrons in the same region (orbital). The same explanation applies to the dip for sulfur after phosphorus in Figure 2.

Ionization energies help confirm the idea that valence electrons are important for chemical combination. The second ionization energy is always larger than the first, the third larger than the second, and so forth because of the greater electrostatic attraction by 1+ and 2+ ions. Successive ionization energies always increase but sometimes the increase is larger than expected. Some data are in Table 1.
| Element | IE1 | IE2 | IE3 | IE4 | IE5 | IE6 | IE7 |
|---|---|---|---|---|---|---|---|
| K | 419 | 3069 | 4438 | 5876 | 7975 | 9620 | 11385 |
| Ca | 590 | 1145 | 4941 | 6465 | 8142 | 10496 | 12350 |
| Sc | 633 | 1244 | 2388 | 7130 | 8877 | 10720 | 13314 |
| Ga | 579 | 1982 | 2962 | 6194 | 8299 | 10874 | 13585 |
| Ge | 760 | 1537 | 3301 | 4409 | 9012 | 11183 | 13981 |
| As | 947 | 1949 | 2731 | 4834 | 6040 | 12302 | 14183 |
| Table 1. Successive Ionization Energies (IEs) for Some Period-4 Elements (kJ/mol) | |||||||
Determine the number of valence electrons and write a Lewis diagram for each atom:
K Sc Ga
Correlate the electron configuration and number of valence electrons with the IE data in Table 1. Write a clear, concise explanation of why the larger IE increases occur where they do.
Exercise 4: Periodic Variation of Ionization Energy
D5.5 Periodic Variation of Electron Affinities
We define electron affinity (EA) as the energy change when an electron is added to an atom to form a negative ion (anion). A table of electron affinity values is in the appendix. The first EA corresponds to adding a single electron to an atom, as shown in this equation:
Many elements have negative EA1, which means that the energy of the 1− anion is lower than the energy of the atom to which the electron was added; that is, the anion is more stable than the atom. For other elements, EA1 is positive, meaning that the anion is less stable than the parent atom.
Analyze the data in the table below, which shows electron affinity values (in kJ/mol) for main-group elements. Apply the ideas about electron configurations that you used in Activity 7 to explain the trends, and exceptions to trends, in electron affinities. Describe the trends and write explanations for them in your notebook.
The properties discussed thus far (size of atoms and ions, effective nuclear charge, ionization energies, and electron affinities) are central to understanding chemical reactivity. For example, because atoms of elements in periodic group 17 (7A) have large ionization energies and large negative electron affinities, it is much easier to form anions than cations. Atoms of elements in periodic groups 1 and 2 (1A and 2A) have very small ionization energies, which means that they can lose electrons relatively easily to form cations. Thus, compounds can be formed when atoms of elements in periodic groups on the left of the table transfer electrons to atoms of elements in groups on the right (except the noble gases). The cations and anions formed this way attract and an ionic compound results.
Metallic substances, which have properties such as high electric conductivity and malleability (the ability to be formed into sheets), are made of atoms whose electrons that can be removed easily; that is, atoms with small ionization energies. Thus, metallic character decreases across a period and increases down a group.
Exercise 5: Equations for Ionization Energy and Electron Affinity
D5.6 Ionic Compounds
When an atom that can lose electrons relatively easily interacts with an atom that readily gain electrons , transfer of one or more electrons can occur, producing an anion and a cation. Atoms that can lose electrons are those with low ionization energy; that is, metals (left side of the periodic table). Atoms that readily gain electrons are those with large negative electron affinities; that is, nonmetals, (right side of the periodic table, except for noble gases).
Lewis diagrams can be used to illustrate the transfer of electrons during the formation of ionic compounds, as shown in Figure 4.
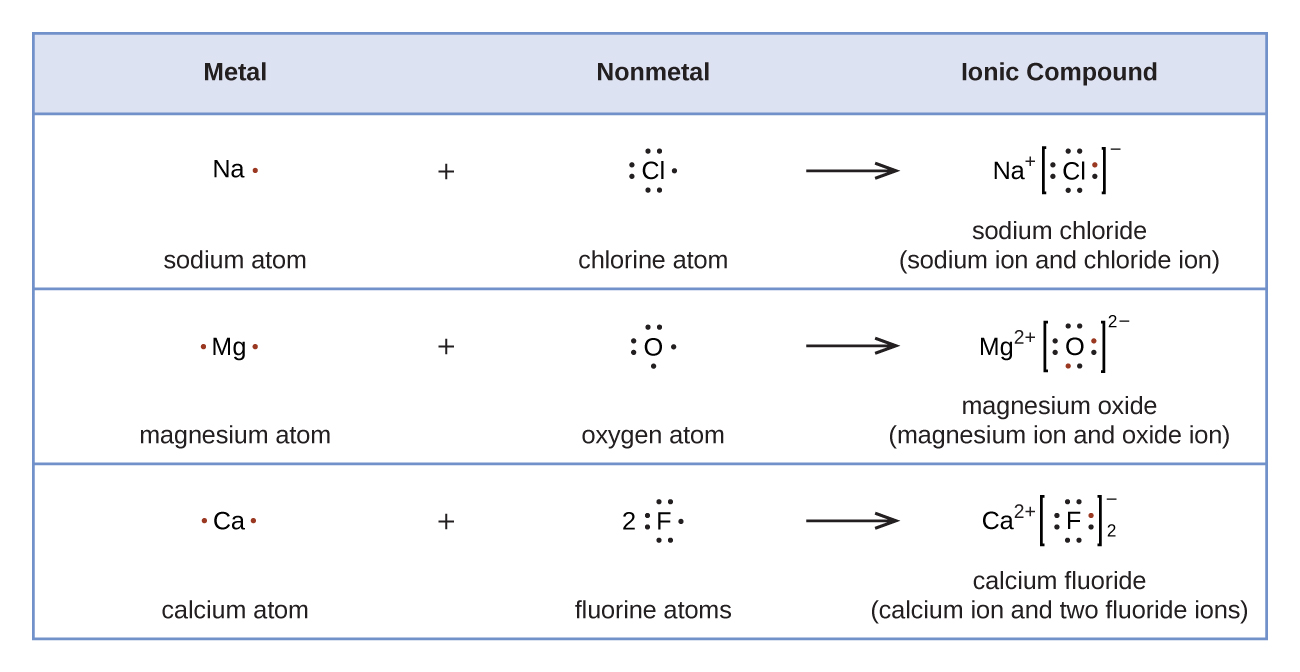
According to Coulomb’s law, anions and cations attract, cations and cations repel, and anions and anions repel. When one anion and one cation form they are attracted and form an ion pair. When a large number of ions form, they combine to form a solid crystal lattice in which anions and cations are arranged so that attractions predominate over repulsions. A compound made up of anions and cations is called an ionic compound and the overall attraction holding it together is called ionic bonding.
For example, when each sodium atom in a sample of sodium metal (group 1 or 1A) gives up one electron to form a sodium cation, Na+, and each bromine atom in a sample of liquid bromine (group 17 or 7A) accepts one electron to form a bromide anion, Br−, the crystal lattice of the compound sodium bromide, which is shown in Figure 4, contains one Na+ ion (green) for each Br− ion (violet). The chemical formula representing the part of the lattice shown in Figure 4 is Na75Br75 because there are 75 Na+ and 75 Br− ions. The actual crystal is much larger so the subscripts in the formula of a real crystal would be huge. A formula unit is a group of chemical symbols that indicates the smallest whole number ratio of ions of each kind that make up the substance. Thus, the formula unit of sodium bromide is NaBr and we say that the formula for sodium bromide is NaBr.
The properties of an ionic compound are determined by the ions the compound is made of and are quite different from the properties of the elements from which the ionic compound was made. For example, both sodium and bromine react with water, but sodium bromide dissolves in water without reacting. Sodium ions and bromide ions do not react with water, but sodium atoms and Br2 molecules do.
Some ions consist of a group of atoms with an overall charge. Examples are sulfate ion, SO42−, dihydrogen phosphate ion, H2PO4−, and ammonium ion, NH4+. It is important to be able to recognize such polyatomic ions and know their charges. A table of polyatomic ions is in the appendix.
Ionic compounds contain cations of metals from the left side of the periodic table and anions of nonmetals from the right side of the periodic table. If a compound’s chemical formula contains a polyatomic ion, then the compound is an ionic compound.
Exercise 6: Identifying Ionic Compounds from Chemical Formulas
All chemical substances must have zero overall electric charge. Thus, in every ionic compound, the total number of positive charges of all cations equals the total number of negative charges of all anions. The subscripts in a formula unit of any ionic compound must result in equal quantities of positive and negative charge. If we know the charges of the ions, then we can write the formula.
Exercise 7: Ionic Compounds with Polyatomic Ions
Exercise 8: Formulas for Ionic Compounds
It is useful to be able to identify ionic compounds from their chemical formulas because all ionic compounds have similar properties. These properties are like the properties of table salt, NaCl and ionic compounds are often referred to as “salts”.
- Ionic compounds have high melting points and boiling points; thus, they are solids at room temperature.
- Ionic compounds are crystalline, have distinct crystal shapes, and are easily cleaved (that is, they break along smooth planes).
- ionic compounds conduct electricity when molten (liquid) but do not conduct when solid. (Click here to see a molten salt conduct.)
- When an ionic compound dissolves in water the solution conducts electricity much better than pure water.
Based on what we have just said about ions, ionic bonding, and crystal lattices, write in your notebook an atomic-scale explanation for each of the four properties of ionic compounds in the list above.
D5.7 Energy, Ions, and Ionic Compounds
Think about the energy changes involved in ionic bonding. As an example consider transfer of an electron from a Li atom to a F atom to form an ion pair, Li+F–, which has lower total energy than the two atoms from which it formed. (The ion pair is more stable than the two atoms.) We can break ion-pair formation into three simpler steps and consider the energy change involved in each:
- Remove the 2s electron from a Li atom to form a Li+ ion.
- Add that same electron to a F atom to form a F– ion.
- Bring the Li+ ion close to the F– ion to form an ion pair.
Based on what you have learned in this unit so far, decide how you could obtain the energy change for each for the three processes involved in ion-pair formation. Describe how you could do a calculation to verify the statement in the text that the energy of the LiF ion pair is lower than the energy of a Li atom and a F atom.
When an ionic crystal lattice (Figure 5) forms energy is lowered even more than for an ion pair because more ions are close together in a structure where attractive forces predominate over repulsive forces. Thus, the calculation in Activity 10 is an underestimate of the stability of a crystal of LiF compared a large number of individual Li and F atoms. The energy of an ionic crystal lattice is lower than for the separated ions by a quantity known as the lattice energy. Lattice energies of ionic compounds can be calculated using a modified form of Coulomb’s law; Table 2 shows results of such calculations.
| Substance | Lattice Energy (kJ/mol) |
|---|---|
| NaI | 682 |
| CaI2 | 1971 |
| MgI2 | 2293 |
| NaOH | 887 |
| Na2O | 2481 |
| NaNO3 | 755 |
| Ca3(PO4)2 | 10,602 |
| CaCO3 | 2804 |
|
Source: Data from CRC Handbook of Chemistry and Physics (2004).
|
|
Based on what you have learned in this unit so far, write in your course notebook an explanation for each item below:
- Compare the lattice energies for NaI, CaI2, and MgI2. Explain why the lattice energies increase.
- Use the lattice energies to decide whether I− has a smaller or larger radius than OH− . Explain your reasoning.
- When an ionic compound dissolves in water, ions separate from the crystal lattice and move among the water molecules. Predict which of the substances in Table 2 is least soluble in water and explain your reasoning.
To summarize the results of Activities 11 and 12, lattice energies are highest for substances with small, highly charged ions. Also, lattice energies can affect physical properties of ionic crystals, such as solubility, melting and boiling points, and hardness.
Podia Question
The formulas and melting points (in °C) of four salts are listed below. All four compounds have the same crystal lattice as NaCl. Write a clear, concise explanation of the differences in melting points using scientifically appropriate language and including any relevant data.
NaF 996 NaCl 801 KCl 770 CaO 2572
Two days before the next whole-class session, this Podia question will become live on Podia, where you can submit your answer.

