M13Q2: Reaction Rates: Identifying Rates on Concentration vs Time Plots; Rates and Reaction Stoichiometry; Defining Average, Instantaneous, and Initial Rates

Chem 103 Textbook Team; Chem 104 Textbook Team

M13Q2: Reaction Rates: Identifying Rates on Concentration vs Time Plots; Rates and Reaction Stoichiometry; Defining Average, Instantaneous, and Initial Rates

Learning Objectives

Write algebraic relationships for rates of reaction based on the stoichiometry of a balanced chemical equation.
| Relative Rates |
Given reactant or product concentration and time data, calculate an average rate, instantaneous rate, and/or the initial rate of reaction.
| Average, Instantaneous, and Initial Rates |

Chemical Kinetics: A Qualitative Approach

To study the kinetics of a reaction, chemists initiate the reaction, measure the concentration of a reactant or product over time as the reaction progresses, and then calculate the change in the concentration per unit time. Plotting the concentration versus time, as seen in Figure 1, is a way to visualize concentration changes as the reaction progresses.

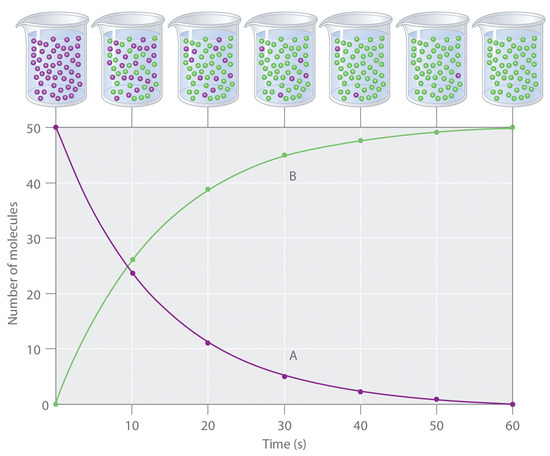
**Figure 1:** The Progress of a Simple Reaction (A → B). The mixture initially contains only A molecules (purple). Over time, the number of A molecules decreases and more B molecules (green) are formed (top). The graph shows the change in the number of A and B molecules in the reaction as a function of time over a 1 min period (bottom). Because the container has a fixed volume, the concentration (atoms/volume or moles/volume) is directly proportional to the number of atoms or moles in the container.

The change in concentration over time of either the reactant or the product over a period of time is often expressed in terms of the change in the reactant concentration.

This rate of change, or rate of decomposition, of the reactant is expressed as follows:

$\displaystyle\begin{array}{rcl} \text{rate of decomposition of A} &= & - \dfrac{\text{change in concentration of reactant}}{\text{time interval}} \\[1.2em] &= & - \dfrac{[\text{A}]_{t_2}\;-\;[\text{A}]_{t_1}}{t_2\;-\;t_1} \\[1.2em] &= & - \dfrac{{\Delta}[\text{A}]}{{\Delta}t} \end{array}$

In this equation, square brackets represent concentration in mol/L so [A]_t₁ represents the concentration of A at time t₁ and Δ[A] represents the change in concentration of A during the time interval Δt (that is, t₂ − t₁). The minus sign is in the equation because reaction rate is defined to be positive. The reactant concentration decreases as the reaction proceeds, making Δ[A] a negative quantity, so a negative sign is needed to make it positive.

Additionally, the rate of change, or rate of formation, of the product is expressed as follows:

$\displaystyle\begin{array}{rcl} \text{rate of formation of B} &= & \dfrac{\text{change in concentration of product}}{\text{time interval}} \\[1.2em] &= & \dfrac{[\text{B}]_{t_2}\;-\;[\text{B}]_{t_1}}{t_2\;-\;t_1} \\[1.2em] &= & \dfrac{{\Delta}[\text{B}]}{{\Delta}t} \end{array}$

In this equation, square brackets represent concentration in mol/L so [B]_t₁ represents the concentration of B at time t₁ and Δ[B] represents the change in concentration of B during the time interval Δt (that is, t₂ − t₁). The product concentration increases as the reaction proceeds, making Δ[B] a positive quantity, so no negative sign is needed to make it positive.

Relative Rate of Reaction

The rate of a reaction may be expressed in terms of the change in the amount of any reactant or product, and may be derived from the stoichiometry of the reaction. Consider the reaction represented by the following equation:

2 NH₃(g) → N₂(g) + 3 H₂(g)

The molar ratio derived from the coefficients in the reaction may be used to relate reaction rates in the same manner that they are used to relate reactant and product amounts. The relation between the reaction rates expressed in terms of nitrogen production and ammonia consumption, for example, is:

$-\dfrac{\Delta \;\text{mol NH}_{3}}{\Delta t} \times \dfrac{1\;\text{mol N}_{2}}{2\;\text{mol NH}_{3}} = \dfrac{\Delta \;\text{mol N}_{2}}{\Delta t}$

We can express this more simply without showing the mole ratio by placing 1/coefficient before each rate expression:

$-\dfrac{1}{2} \dfrac{\Delta \;\text{mol NH}_{3}}{\Delta t} = \dfrac{\Delta \; \text{mol N}_{2}}{\Delta t}$

Note that a negative sign has been added to account for the opposite signs of the two amount changes (the reactant amount is decreasing while the product amount is increasing). If the reactants and products are present in the same solution, the molar amounts may be replaced by concentrations:

$-\dfrac{1}{2} \dfrac{\Delta [\text{NH}_{3}]}{\Delta t} = \dfrac{\Delta [\text{N}_{2}]}{\Delta t}$

Similarly, the rate of formation of H₂ can be related to the rate of formation of N₂ as follows:

$\dfrac{1}{3} \dfrac{\Delta [\text{H}_{2}]}{\Delta t} = \dfrac{\Delta [\text{N}_{2}]}{\Delta t}$

Put all together and in relation to the overall rate of reaction, the relative rate expression will be:

rate = $-\dfrac{1}{2} \dfrac{\Delta [\text{NH}_{3}]}{\Delta t} = \dfrac{\Delta [\text{N}_{2}]}{\Delta t} = \dfrac{1}{3} \dfrac{\Delta [\text{H}_{2}]}{\Delta t}$

Example 1

Expressions for Relative Reaction Rates
The first step in the production of nitric acid is the combustion of ammonia:

4 NH₃(g) + 5 O₂(g) → 4 NO(g) + 6 H₂O(g)

Write the equations that relate the rates of consumption of the reactants and the rates of formation of the products.

Solution
Considering the stoichiometry of this homogeneous reaction, the rates for the consumption of reactants and formation of products are:

$-\dfrac{1}{4} \dfrac{\Delta [\text{NH}_{3}]}{\Delta t} = -\dfrac{1}{5} \dfrac{\Delta [\text{O}_{2}]}{\Delta t} = \dfrac{1}{4} \dfrac{\Delta [\text{NO}]}{\Delta t} = \dfrac{1}{6} \dfrac{\Delta [\text{H}_{2}\text{O}]}{\Delta t}$

Check Your Learning
The rate of formation of Br₂ is 6.0 × 10⁻⁶ M/s in a reaction described by the following net ionic equation:

5 Br^–(aq) + BrO₃^–(aq) → 3 Br₂(aq) + 3 H₂O(aq)

Write the equations that relate the rates of consumption of the reactants and the rates of formation of the products.

Answer:

$-\dfrac{1}{5} \dfrac{\Delta [\text{Br}^{-}]}{\Delta t} = -\dfrac{\Delta [\text{BrO}_{3}^{-}]}{\Delta t} = \dfrac{1}{3} \dfrac{\Delta [\text{Br}_{2}]}{\Delta t} = \dfrac{1}{3} \dfrac{\Delta [\text{H}_{2}\text{O}]}{\Delta t}$

Initial, Instantaneous, and Average Rates

If we measure the concentration of hydrogen peroxide, H₂O₂, in an aqueous solution, we find that it changes slowly over time as the H₂O₂ decomposes, according to the equation:

2 H₂O₂(aq) → 2 H₂O(ℓ) + O₂(g)

To obtain the tabulated results for this decomposition shown in Figure 2, the concentration of hydrogen peroxide was measured every 6 hours over the course of a day at a constant temperature of 40 °C. Reaction rates were computed for each time interval by dividing the change in concentration by the corresponding time increment, as shown here for the first 6-hour period:

$-\dfrac{\Delta [\text{H}_{2}\text{O}_{2}]}{\Delta t} = \dfrac{-(0.500\;\text{M} - 1.000\;\text{M})}{(6.00 \; \text{hr} - 0.00\; \text{hr}) }$ = 0.0833 M/hr

Notice that the reaction rates vary with time, decreasing as the reaction proceeds. Results for the last 6-hour period yield a reaction rate of:

$-\dfrac{\Delta [\text{H}_{2}\text{O}_{2}]}{\Delta t} = \dfrac{-(0.0625\;\text{M} - 0.125\;\text{M})}{(24.00 \; \text{hr} - 18.00\; \text{hr}) }$ = 0.0103 M/hr

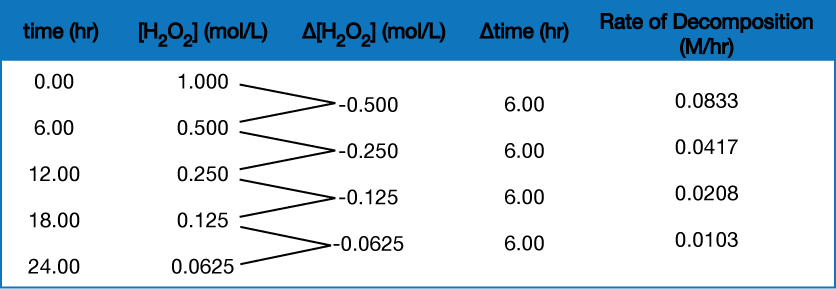
**Figure 2.** The rate of decomposition of H₂O₂ in an aqueous solution decreases as the concentration of H₂O₂ decreases.

This behavior indicates the reaction continually slows with time. Using the concentrations at the beginning and end of a time period results in the calculation of an average rate for the reaction over this time interval. At any specific time, the rate at which a reaction is proceeding is known as its instantaneous rate. The instantaneous rate of a reaction at “time zero,” when the reaction commences, is its initial rate.

Consider the analogy of a car slowing down as it approaches a stop sign. The vehicle’s initial rate—analogous to the beginning of a chemical reaction—would be the speedometer reading at the moment the driver begins pressing the brakes (t₀). A few moments later, the instantaneous rate at a specific moment—call it t₁—would be somewhat slower, as indicated by the speedometer reading at that point in time. As time passes, the instantaneous rate will continue to fall until it reaches zero, when the car (or reaction) stops. Unlike instantaneous speed, the car’s average speed is not indicated by the speedometer; but it can be calculated as the ratio of the distance traveled to the time required to bring the vehicle to a complete stop (Δt). Like the decelerating car, the average rate of a chemical reaction will fall somewhere between its initial and final rates.

The instantaneous rate of a reaction may be determined one of two ways. If experimental conditions permit the measurement of concentration changes over very short time intervals, then average rates computed as described earlier provide reasonably good approximations of instantaneous rates. Alternatively, a graphical procedure may be used that, in effect, yields the results that would be obtained if short time interval measurements were possible. If we plot the concentration of hydrogen peroxide against time, the instantaneous rate of decomposition of H₂O₂ at any time t is given by the slope of a straight line that is tangent to the curve at that time (Figure 3).

A graph is shown with the label, “Time ( h ),” appearing on the x-axis and “[ H subscript 2 O subscript 2 ] ( mol L superscript negative 1)” on the y-axis. The x-axis markings begin at 0 and end at 24. The markings are labeled at intervals of 6. The y-axis begins at 0 and includes markings every 0.200, up to 1.000. A decreasing, concave up, non-linear curve is shown, which begins at 1.000 on the y-axis and nearly reaches a value of 0 at the far right of the graph around 10 on the x-axis. A red tangent line segment is drawn on the graph at the point where the graph intersects the y-axis. A second red tangent line segment is drawn near the middle of the curve. A vertical dashed line segment extends from the left endpoint of the line segment downward to intersect with a similar horizontal line segment drawn from the right endpoint of the line segment, forming a right triangle beneath the curve. The vertical leg of the triangle is labeled “capital delta [ H subscript 2 O subscript 2 ]” and the horizontal leg is labeled, “capital delta t.” — **Figure 3**. This graph shows a plot of concentration versus time for a 1.000 M solution of H₂O₂. The rate at any instant is equal to the opposite of the slope of a line tangential to this curve at that time. Tangents are shown at t = 0 h (“initial rate”) and at t = 10 h (“instantaneous rate” at that particular time).

Chemistry in Real Life: Test Strips for Urinalysis

Physicians often use disposable test strips to measure the amounts of various substances in a patient’s urine (Figure 4). These test strips contain various chemical reagents, embedded in small pads at various locations along the strip, which undergo changes in color upon exposure to sufficient concentrations of specific substances. The usage instructions for test strips often stress that proper read time is critical for optimal results. This emphasis on read time suggests that kinetic aspects of the chemical reactions occurring on the test strip are important considerations.

The test for urinary glucose relies on a two-step process represented by the chemical equations shown here:

C₆H₁₂O₆ + O₂ $\xrightarrow{catalyst}$ C₆H₁₀O₆

2 H₂O₂ + 2 I^– $\xrightarrow{catalyst}$ I₂ + H₂O + O₂

The first equation depicts the oxidation of glucose in the urine to yield glucolactone (C₆H₁₀O₆) and hydrogen peroxide. The hydrogen peroxide produced subsequently oxidizes colorless iodide ion to yield brown molecular iodine, which may be visually detected. Some strips include an additional substance that reacts with iodine to produce a more distinct color change.

The two test reactions shown above are inherently very slow, but their rates are increased by special enzymes embedded in the test strip pad. This is an example of catalysis. A typical glucose test strip for use with urine requires approximately 30 seconds for completion of the color-forming reactions. Reading the result too soon might lead one to conclude that the glucose concentration of the urine sample is lower than it actually is (a false-negative result). Waiting too long to assess the color change can lead to a false positive due to the slower (not catalyzed) oxidation of iodide ion by other substances found in urine.

A photograph shows 8 test strips laid on paper toweling. Each strip contains 11 small sections of various colors, including yellow, tan, black, red, orange, blue, white, and green. — **Figure 4**. Test strips are commonly used to detect the presence of specific substances in a person’s urine. Many test strips have several pads containing various reagents to permit the detection of multiple substances on a single strip. (credit: Iqbal Osman)

Key Concepts and Summary

In the last section, we looked at how we could predict the rate of reaction qualitatively, but in this section, we begin to look at chemical kinetics in a quantitative way. The rate of reaction is defined as the change in concentration or a reactant or product over the change in time. The time range a rate is calculated over is extremely important – using the very initial time point gives us the initial rate, while using later time points will give us an instantaneous or average rate, depending on the length of time averaged over. Once we know the rate of reaction for a single reactant or product, we can use the mole ratio of coefficients from the balanced reaction to calculate the rate of reaction for any species present in the reaction.

Key Equations

aA + bB → cC + dD
$-\dfrac{1}{a}\dfrac{\Delta[\text{A}]}{\Delta t} = -\dfrac{1}{b}\dfrac{\Delta[\text{B}]}{\Delta t} =\dfrac{1}{c}\dfrac{\Delta[\text{C}]}{\Delta t} = \dfrac{1}{d}\dfrac{\Delta[\text{D}]}{\Delta t}$
rate of decomposition of A = $-\dfrac{[\text{A}]_{t_2} - [\text{A}]_{t_1}}{t_{2}-t_{1}} = - \dfrac{\Delta[\text{A}]}{\Delta t}$
rate of formation of B = $\dfrac{[\text{B}]_{t_2} - [\text{B}]_{t_1}}{t_{2}-t_{1}} = \dfrac{\Delta[\text{B}]}{\Delta t}$

Glossary

average rate: the rate calculated using the first and last time measurements within a given time period

initial rate: the rate at “time zero” when the reaction commences, calculated using the initial concentration at time zero and at a point soon thereafter

instantaneous rate: the rate at a specific point in time, calculated using calculus or very small time changes around the desired point

reaction rate: often expressed as the change in concentration of a reactant (or product) divided by the change in time

relative rate: a rate of reaction expressed between two molecules using a molar ratio derived from the coefficients from a balanced chemical reaction

Chemistry End of Section Exercises

What is the difference between average rate, initial rate, and instantaneous rate?
Ozone decomposes to oxygen according to the equation 2 O₃(g) ⟶ 3 O₂(g). Write the equation that relates the rate expressions for this reaction in terms of the disappearance of O₃ and the formation of oxygen.
In the nuclear industry, chlorine trifluoride is used to prepare uranium hexafluoride, a volatile compound of uranium used in the separation of uranium isotopes. Chlorine trifluoride is prepared by the reaction Cl₂(g) + 3 F₂(g) ⟶ 2 ClF₃(g). Write the equation that relates the rate expressions for this reaction in terms of the disappearance of Cl₂ and F₂ and the formation of ClF₃.
Consider the reaction:
C₆H₁₄(g) → C₆H₆(g) + 4 H₂(g)

If the rate of appearance of H₂ at a particular moment during the reaction is 0.026 M/s, what is the rate of disappearance of C₆H₁₄ at that time?

Answers to Chemistry End of Section Exercises

The instantaneous rate is the rate of a reaction at any particular point in time, a period of time that is so short that the concentrations of reactants and products change by a negligible amount. The initial rate is the instantaneous rate of reaction as it starts (as product just begins to form). Average rate is the average of the instantaneous rates over a time period.
rate = $-\dfrac{1}{2} \dfrac{\Delta[\text{O}_{3}]}{\Delta t} = +\dfrac{1}{3} \dfrac{\Delta[\text{O}_{2}]}{\Delta t}$
rate = $-\dfrac{1}{1} \dfrac{\Delta[\text{Cl}_{2}]}{\Delta t} = -\dfrac{1}{3} \dfrac{\Delta[\text{F}_{2}]}{\Delta t} = +\dfrac{1}{2} \dfrac{\Delta[\text{ClF}_{3}]}{\Delta t}$
0.0065 M/s

Left-click here to watch Exercise 4 problem solving video.

Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 103/104 Resource Book Copyright © by Chem 103 Textbook Team and Chem 104 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.