M16Q6: Titration of a Weak Acid with a Strong Base; Titration of a Weak Base with a Strong Acid

Chem 103 Textbook Team; Chem 104 Textbook Team

M16Q6: Titration of a Weak Acid with a Strong Base; Titration of a Weak Base with a Strong Acid

Learning Objectives

Identify key species present in the titration of a weak acid by a strong base (or a weak base by a strong acid).
Determine pH and concentrations of chemical species at any point in the titration of a weak acid by a strong base or a weak base by a strong acid.
| Titrations Flow Chart |
Determine the K_a or K_b value for a weak acid or weak base from a given titration curve, as well as the equivalence point for the titration.

The titration of a weak acid with a strong base (or of a weak base with a strong acid) follows the same general principle as those discussed for a strong acid/strong base titration but typically has an extra step or two in the calculations. Let us consider the titration of 25.0 mL of 0.100 M acetic acid (a weak acid) with 0.100 M sodium hydroxide and compare the titration curve with that of the strong acid (Figure 1).

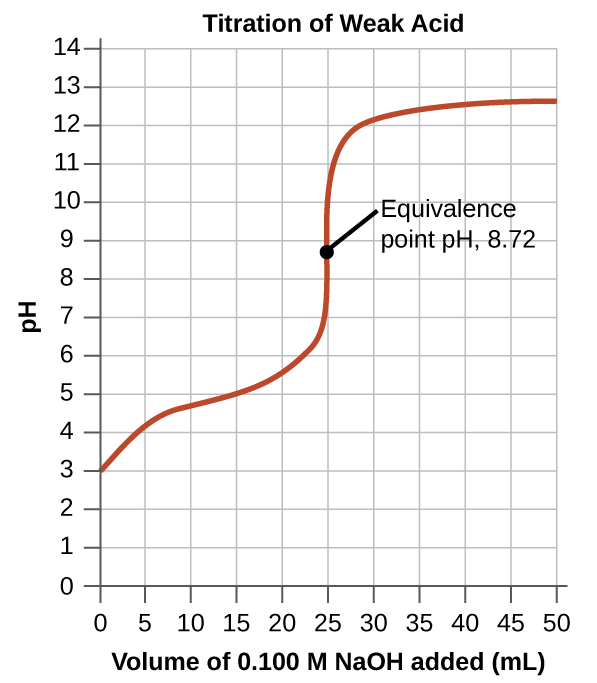
The graph in this figure is titled “Titration of Weak Acid.” The horizontal axis is labeled “Volume of 0.100 M N a O H added (m L).” Markings and vertical gridlines are provided every 5 units from 0 to 50. The vertical axis is labeled “p H” and is marked every 1 unis beginning at 0 extending to 14. A red curve is drawn on the graph which increases steadily from the point (0, 3) up to about (20, 5.5) after which the graph has a vertical section from (25, 7) up to (25, 11). The graph then levels off to a value of about 12.5 from about 40 m L up to 50 m L. The midpoint of the vertical segment of the curve is labeled “Equivalence point p H, 8.72.” — **Figure 1.** The titration curve for the titration of 25.00 mL of 0.100 M CH₃COOH (weak acid) with 0.100 M NaOH (strong base) has an equivalence point of 8.72 pH.

Although the initial volume and molarity of the acids are the same, there are important differences between the two titration curves. The titration curve for the weak acid begins at a higher value (less acidic) and maintains higher pH values up to the equivalence point. The pH at the equivalence point is also higher (8.72 rather than 7.00) due to the presence of the acetate ion and water at the equivalence point:

CH₃COOH(aq) + OH^–(aq) → CH₃COO^–(aq) + H₂O(ℓ)

After the equivalence point, the two curves are identical because the pH is only dependent on the excess hydroxide added in both cases.

Example 1

Titration of a Weak Acid with a Strong Base
The titration curve shown in Figure 1 is for the titration of 25.00 mL of 0.100 M CH₃COOH with 0.100 M NaOH. The reaction can be represented as:

CH₃COOH(aq) + OH^–(aq) → CH₃COO^–(aq) + H₂O(ℓ)

What is the initial pH before any amount of the NaOH solution has been added? K_a = 1.8 × 10⁻⁵ for CH₃COOH.
Find the pH after 12.50 mL of the NaOH solution have been added.
Find the pH after 25.00 mL of the NaOH solution has been added.
Find the pH after 37.50 mL of the NaOH solution has been added.

Solution
(a) Since there is only a weak acid in solution, we can use an ICE table to aid is in calculating the pH:

CH₃COOH(aq) + H₂O(ℓ) ⇌ CH₃COO^–(aq) + H₃O⁺(aq)

I (Intial)

0.100

–

0

C (Change)

–x

–

+x

E (Equilibrium)

0.100 – x

–

x

Assuming that the dissociated amount is small compared to 0.100 M, we find that:

K_a = $\dfrac{[\text{H}_{3}\text{O}^{+}][\text{CH}_{3}\text{COO}^{-}]}{[\text{CH}_{3}\text{COOH}]} = \dfrac{x^{2}}{0.100 - x} \approx \dfrac{x^{2}}{0.100}$ = 1.8 × 10^-5

x = ((1.8 × 10^-5) × (0.100))^½ = 1.3 × 10^-3

pH = -log[H₃O⁺] = -log(1.3 × 10^-3) = 2.87

(b) Since we have a weak acid and a strong base reacting, we first start with writing out the balanced reaction and setting up an SCF table with the starting moles of each species:

25.00 mL × $\dfrac{1\ \text{L}}{1000\ \text{mL}} \times \dfrac{0.100\ \text{moles CH}_{3}\text{COOH}}{1\ \text{L}}$ = 0.002500 moles CH₃COOH

12.50 mL × $\dfrac{1\ \text{L}}{1000\ \text{mL}} \times \dfrac{0.100\ \text{moles OH}^-}{1\ \text{L}}$ = 0.001250 moles OH^–

CH₃COOH(aq) + OH^–(aq) → CH₃COO^–(aq) + H₂O(ℓ)

S (Start)

0.002500

0.001250

0

–

C (Change)

F (Finish)

Then, we subtract the smaller number of moles between the reactants, ensuring that one of the reactants goes to zero and other reactant’s remaining quantity is positive.

	CH₃COOH(aq) + OH^–(aq) → CH₃COO^–(aq) + H₂O(ℓ)
S (Start)	0.002500	0.001250	0	–
C (Change)	-0.001250	-0.001250	+0.001250	–
F (Finish)	0.001250	0	0.001250	–

The last step is to ask ourselves “What’s left in the beaker?” We have the conjugate acid/base pair left in the beaker, so we can use the Henderson-Hasselbalch equation to solve for the pH.

pH = pK_a + log $\dfrac{[\text{base}]}{[\text{acid}]}$ = -log(1.8 × 10^-5) + log $\dfrac{0.001250}{0.001250}$ = 4.74

Notice that the pH is equal to the pK_a. We could have predicted this since the moles of conjugate base are equal to the moles of acid! This represents the half-equivalence point of the titration.

(c) Since we have a weak acid and a strong base reacting, we first start with writing out the balanced reaction and setting up an SCF table with the starting moles of each species:

25.00 mL × $\dfrac{1\ \text{L}}{1000\ \text{mL}} \times \dfrac{0.100\ \text{moles CH}_{3}\text{COOH}}{1\ \text{L}}$ = 0.002500 moles CH₃COOH

25.00 mL × $\dfrac{1\ \text{L}}{1000\ \text{mL}} \times \dfrac{0.100\ \text{moles OH}^-}{1\ \text{L}}$ = 0.002500 moles OH^–

CH₃COOH(aq) + OH^–(aq) → CH₃COO^–(aq) + H₂O(ℓ)

S (Start)

0.002500

0

–

C (Change)

F (Finish)

Then, we subtract the smaller number of moles between the reactants, ensuring that one of the reactants goes to zero and other reactant’s remaining quantity is positive (or zero).

	CH₃COOH(aq) + OH^–(aq) → CH₃COO^–(aq) + H₂O(ℓ)
S (Start)	0.002500	0.002500	0	–
C (Change)	-0.002500	-0.002500	+0.002500	–
F (Finish)	0	0	0.002500	–

The last step is to ask ourselves “What’s left in the beaker?” We have only the conjugate base and water left in solution (a weak base solution). In order to solve for the pH of a weak base, we need to flip the reaction, set up an ICE table, and calculate the new concentration of the conjugate base, and set up a K_b expression.

[CH₃COO^–] = $\dfrac{0.002500\ \text{moles}}{0.05000\ \text{L}}$ = 0.0500 M CH₃COO^–

CH₃COO^–(aq) + H₂O(ℓ) ⇌ CH₃COOH(aq) + OH^–(aq)

I (Intial)

0.0500

–

0

C (Change)

–x

–

+x

E (Equilibrium)

0.0500 – x

–

x

K_b = $\dfrac{K_{w}}{K_{a}} = \dfrac{1.0 \times 10^{-14}}{1.8 \times 10^{-5}}$ = 5.6 × 10^-10

K_b = $\dfrac{[\text{OH}^{-}][\text{CH}_{3}\text{COOH}]}{[\text{CH}_{3}\text{COO}^{-}]} = \dfrac{x^{2}}{0.0500 - x} \approx \dfrac{x^{2}}{0.0500}$ = 5.6 × 10^-10

x = ((5.6 × 10^-10) × (0.0500))^½ = 5.3 × 10^-6

pOH = -log[OH^–] = -log(5.3 × 10^-6) = 5.28

pH = 14.00 – pOH = 14.00 – 5.28 = 8.72

Note that the pH at the equivalence point of this titration is greater than 7 since only the weak base remains at the equivalence point!

(d) Since we have a weak acid and a strong base reacting, we first start with writing out the balanced reaction and setting up an SCF table with the starting moles of each species:

25.00 mL × $\dfrac{1\ \text{L}}{1000\ \text{mL}} \times \dfrac{0.100\ \text{moles CH}_{3}\text{COOH}}{1\ \text{L}}$ = 0.002500 moles CH₃COOH

37.50 mL × $\dfrac{1\ \text{L}}{1000\ \text{mL}} \times \dfrac{0.100\ \text{moles OH}^-}{1 \text{L}}$ = 0.003750 moles OH^–

CH₃COOH(aq) + OH^–(aq) → CH₃COO^–(aq) + H₂O(ℓ)

S (Start)

0.002500

0.003750

0

–

C (Change)

F (Finish)

Then, we subtract the smaller number of moles between the reactants, ensuring that one of the reactants goes to zero and other reactant’s remaining quantity is positive.

	CH₃COOH(aq) + OH^–(aq) → CH₃COO^–(aq) + H₂O(ℓ)
S (Start)	0.002500	0.003750	0	–
C (Change)	-0.002500	-0.002500	+0.002500	–
F (Finish)	0	0.001250	0.002500	–

The last step is to ask ourselves “What’s left in the beaker?” We have both excess strong base and the conjugate weak base. We can use a very accurate approximation here to make solving for the pH much easier. The excess strong base will affect the pH much, MUCH more than the leftover conjugate weak base. So we will approximate the pH by the strong base alone by first calculating the concentration of the [OH^–].

[OH^–] = $\dfrac{0.001250\ \text{moles OH}^{-}}{0.06250\ \text{L}}$ = 0.0200 M OH^–

pOH = -log[OH^–] = -log(0.0200) = 1.70

pH = 14.00 – pOH = 14.00 – 1.70 = 12.30

Note that this result is the same as for the strong acid-strong base titration example provided earlier in this chapter, since the amount of the strong base added moves the solution past the equivalence point.

Check Your Learning
Calculate the pH for the weak acid/strong base titration between 50.0 mL of 0.100 M HCOOH(aq) (formic acid) and 0.200 M NaOH (titrant) at the listed volumes of added base: 0.00 mL, 15.0 mL, 25.0 mL, and 30.0 mL. (K_a of HCOOC is 3.0 × 10^-4)

Answer:

0.00 mL, pH = 2.26
15.0 mL, pH = 3.70
25.00 mL, pH= 8.17
30.0 mL, pH = 12.097

Flow Chart for Acid & Base Problems

Solving for concentrations and pH values in acid/base reactions can seem confusing how to approach at first. However, there are four primary scenarios that you will encounter, shown in Figure 2 below.

The first scenario is in green, when you only have a weak acid or a weak base in water. We encounter these problems earlier this semester when studying acids and bases. (See Example 5-7 in M15Q5.) Since both reactants are weak and do not dissociate 100%, the first step will be to write out the correct reaction and set up an ICE table.
The second scenario is in red, when you only have a strong acid or a strong base in water. We also encountered these types of problems earlier this semester when studying acids and bases. (See Example 3 and 5 in M15Q4.)
The third scenario is in blue, when you have both an acid and a base reacting and one or both of them is strong. These represent a typical titration problem and will require the most work of the four scenarios as there is always a second step to finish the problem.
- Once you have fully reacted the acid and base, you must look at the “F” row in your SCF table to determine what is left in your beaker. There are three possible outcomes, which just happen to be the three other scenarios in the flow chart!
  - If you only have a weak acid or base with water left (which occurs in weak/strong titrations at the equivalence point), you must calculate the concentration of the remaining weak acid or base (by dividing by total volume), set up an ICE table, and use the appropriate equilibrium constant K.
  - If you only have a strong acid or base left (which occurs often in a strong/strong titration or after the equivalence point in a weak/strong titration), you must calculate the concentration of the remaining strong acid or base (by dividing by total volume).
  - If you have a buffer remaining (the weak conjugate acid/base pair, which occurs often before the equivalence point in a weak/strong titration), you can plug the moles directly into the Henderson-Hasselbalch equation, assuming everything is in the same beaker.
The fourth scenario is in purple, when you have a weak acid-base pair that are also conjugates of each other. This is a buffer solution and you can use the Henderson-Hasselbalch equation to solve the problem.

This figure contains a flow chart, beginning with a black box with the text “What’s in my beaker?” There are four arrows going from this black box. To the left is a green arrow pointing towards a green box with the text “only weak acid or base + H 2 O, I C E Table, (Need K a or K b)”. Pointing down to the left is a red arrow to a red box with the text “only strong acid or base, p H = - log [H 3 O +] or p O H”. Pointing down to the right is a blue arrow to a blue box with the text “acid and base, (one or both strong), balanced reaction, S C F Table, What’s left?”. Pointing to the right is a purple arrow to a purple box that says “acid and base, (both weak & conjugate pair), buffer, Find p H using Henderson-Hasselbalch Equation”. Pointing down from the blue box are three more arrows. A red arrow points to the left to the red box with “Divide by Total Volume” above the arrow. A green arrow points to the left to the green box with “Divide by Total Volume, Flip Reaction” above the arrow. The purple arrow points to the right to the purple box. — **Figure 2.** “What’s in my beaker?” flow chart.

Chemistry End of Section Exercises

At what point in the titration of a weak acid (analyte) with a strong base (titrant) is the pH calculated using the concentration of the weak acid’s conjugate base and the K_b?
1. The initial pH before any strong base is added.
2. The half-equivalence point.
3. The equivalence point.
4. At any point after the equivalence point.
5. When a large excess of strong base has been added.
The curve for the titration of 40.0 mL of 0.10 M trimethylamine, (CH₃)₃N, with 0.10 M hydrochloric acid, HCl, is shown below.
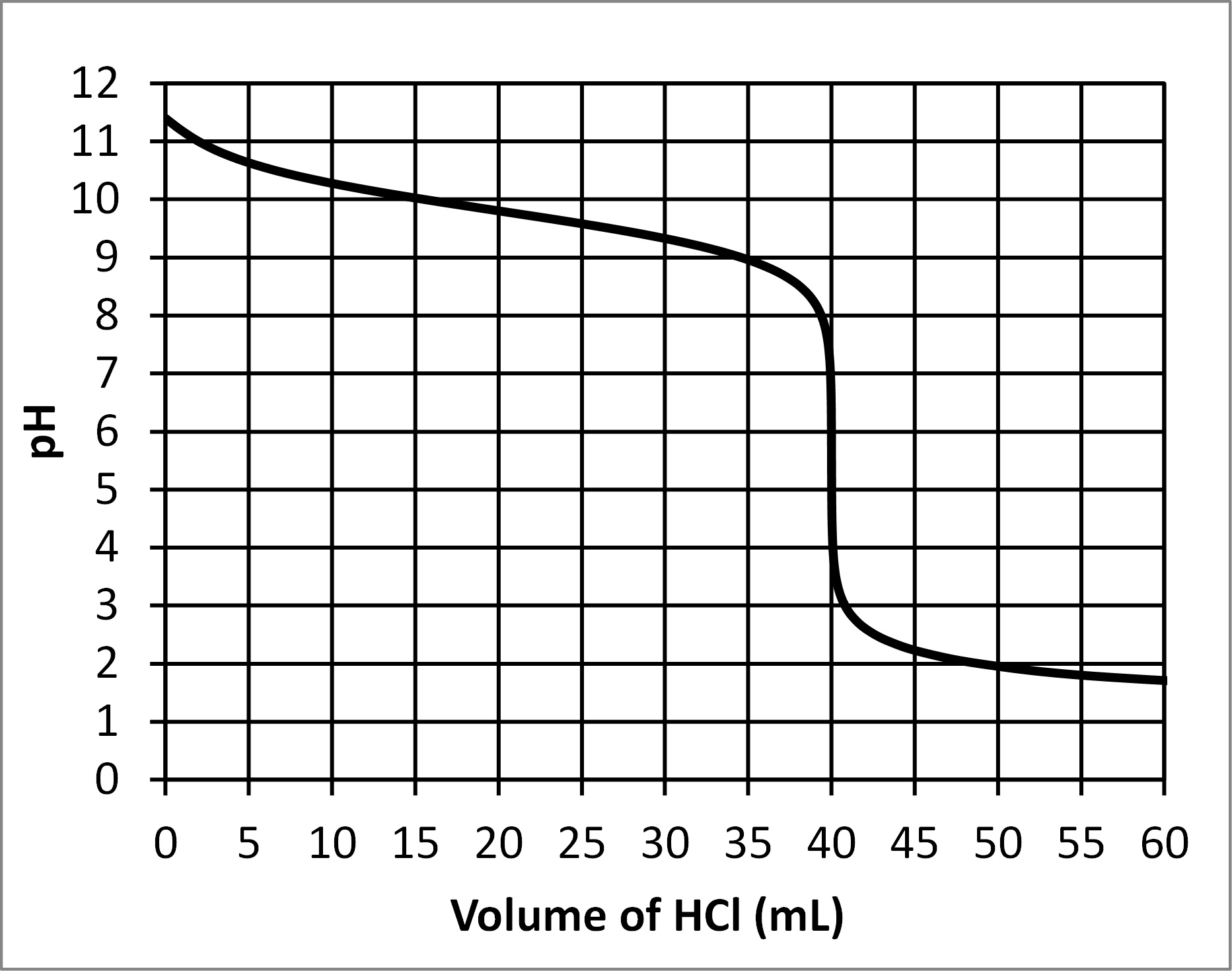
1. What is the pH at the equivalence point in this titration?
2. What is the pK_a of the trimethylammonium ion?
In a general chemistry lab session, 50.0 mL 1.00 M HNO₂ is titrated with 0.500 M NaOH. (The K_a of HNO₂ is 7.41 × 10^-4)
1. Write the net ionic equation for the titration reaction that occurs when 50.0 mL of 1.00 M HNO₂ is titrated with 0.500 M NaOH.
2. Are there spectator ions present? If so, what are they and how will they affect the pH?
3. How many moles of NaOH will be added to the analyte to reach the equivalence point?
4. How many mL of NaOH will be added to the analyte to reach the equivalence point?
5. What is the pH at the equivalence point?
In a general chemistry lab session, 100.0 mL of 1.00 M NH₃ is titrated with 0.600 M HCl. (The K_b of NH₃ is 1.77 × 10^-5)
1. Write the net ionic equation for the titration reaction that occurs when 100.0 mL 1.00 M NH₃ is titrated with 0.600 M HCl.
2. Are there spectator ions present? If so, what are they and how will they affect the pH?
3. How many moles of HCl will be added to the analyte to reach the equivalence point?
4. How many mL of HCl will be added to the analyte to reach the equivalence point?
5. What is the pH at the equivalence point?
60.0 mL of a 0.050 M CH₃COOH solution is titrated with a 0.075 M NaOH solution. How many mL of base must be added to get to the equivalence point? (The K_a of CH₃COOH = 1.8 × 10^-5)
Calculate the pH at the equivalence point for the titration of 0.20 M HCl with 0.20 M NH₃. (K_b(NH₃) = 1.8 × 10^-5).
0.25 M ethylamine, C₂H₅NH₂ (K_b= 4.3 × 10^-4), is titrated with 0.50 M HCl. 50.0 mL of the C₂H₅NH₂ is placed in an Erlenmeyer flask and the HCl added slowly from the buret as the pH is recorded. The initial pH before any HCl(aq) is added is 12.02.
1. Write a balanced chemical equation that describes the above reaction.
2. What volume of HCl(aq) is required to get to the equivalence point?
3. What will be the approximate pH at the equivalence point?
  1. < 7.00
  2. = 7.00
  3. > 7.00
4. What conjugate acid/base pair is present at the half equivalence point?
5. What is the pH of the solution at the half equivalence point?
6. What is the pH after the addition of 15.0 mL of HCl(aq)?
7. What is the pH of the solution at the equivalence point?
80.0 mL of 0.100 M NH₃ is titrated with 0.200 M HClO₄. (The K_b of NH₃ is 1.77 × 10^-5) Calculate the pH at the following points:
1. Initially, before any HClO₄ has been added
2. When 15.0 mL HClO4 has been added
3. When 32.0 mL HClO4 has been added
4. When 40.0 mL HClO₄ has been added
5. When 80.0 mL HClO₄ has been added
Consider the table and plot below.

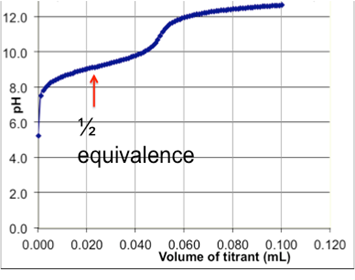
Base K_b Conjugate Acid

CO₃^2- 10^-10 HCO₃^–

NH₃ 10^-5 NH₄⁺

CH₃COO^– 10^-9 CH₃COOH

H^S- 10^-7 H₂S

Which acid is being titrated with a strong base? Justify your answer in a few sentences using clear reference to the graph and table above.
1. HCO₃^–
2. NH₄⁺
3. CH₃COOH
4. H₂S
5. HCl
The titration curves labeled “1” and “2” were obtained by titrating equal volumes of two different acid solutions with the same sodium hydroxide solution.

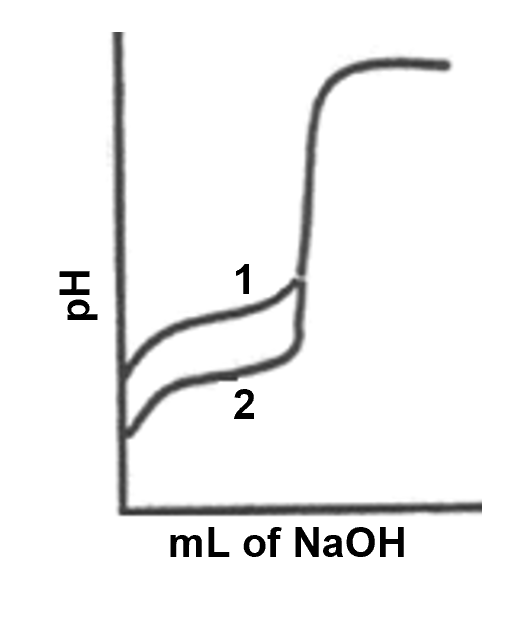
What conclusions can be drawn about the relative concentrations and strengths of acids 1 and 2 from these curves? Justify your answer in a few sentences.
1. The concentrations are the same but acid 1 is weaker than acid 2.
2. The concentrations are the same but acid 1 is stronger than acid 2.
3. Acid 1 is the same strength as acid 2, but it is less concentrated.
4. Acid 1 is the same strength as acid 2, but it is more concentrated.
5. Acid 1 is more concentrated and a stronger acid than acid 2.

Answers to Chemistry End of Section Exercises

C
(a) 5.6; (b) 9.8
(a) HNO₂(aq) + OH^–(aq) → NO₂^–(aq) + H₂O(ℓ)
(b) Na⁺; this is a neutral ion and will not affect the pH
(c) 0.0500 moles
(d) 1.00 × 10² mL
(e) 8.327
(a) NH₃(aq) + H₃O⁺(aq) → NH₄⁺(aq) + H₂O(ℓ)
(b) Cl^–; this is a neutral ion and will not affect the pH
(c) 0.100 moles
(d) 167 mL
(e) 4.837
40.0 mL
5.12
(a) C₂H₅NH₂(aq) + H₃O⁺(aq) → C₂H₅NH₃⁺(aq) + H₂O(ℓ)
(b) 25.0 mL
(c) A
(d) C₂H₅NH₂/C₂H₅NH₃⁺
(e) 10.63
(f) 10.45
(g) 5.71
(a) 11.124; (b) 9.470; (c) 8.646; (d) 5.212; (e) 1.301
B. At the ½ equivalence point, pH = pK_a, in this case the pH at the ½ equivalence point can be estimated to be 9. At a pH of 9, the pK_a would be 10^-9 and the pK_b would be 10^-5. This makes NH₄⁺ the acid being titrated.
A. For both titrations, it takes the same volume of titrant to reach the equivalence point, meaning that the same number of moles of acid were present in the beaker. Since we were titrating the same volume of acid, the concentration also has to be the same. Since the concentration of the two acids is the same, the difference in the initial pH is related to the strength of the acid. A weaker acid would dissociate less, leading to less H₃O⁺ ions in solution, and therefore a lower initial pH. Therefore, acid 1 is weaker than acid 2.

Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 103/104 Resource Book Copyright © by Chem 103 Textbook Team and Chem 104 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.