M17Q3: Second Law of Thermodynamics
Learning Objectives
- Calculate the entropy change for a process occurring at constant temperature.
- Calculate the change in entropy for a chemical reaction using standard molar entropy values.
| Key Concepts and Summary | Key Equations | Glossary | End of Section Exercises |
The Second Law of Thermodynamics
In the quest to identify a property that may reliably predict the spontaneity of a process, we have identified a very promising candidate: entropy. Processes that involve an increase in entropy of the system (ΔS > 0) are very often spontaneous; however, examples to the contrary are plentiful. By expanding consideration of entropy changes to include the surroundings, we may reach a significant conclusion regarding the relation between this property and spontaneity. In thermodynamic models, the system and surroundings comprise everything, that is, the universe, and so the following is true:
ΔSuniv = ΔSsys + ΔSsurr
To illustrate this relationship, consider again the process of heat flow between two objects, one identified as the system and the other as the surroundings. There are three reasonable possibilities for such a process:
- The objects are at different temperatures, and heat flows from the hotter to the cooler object. This always occurs spontaneously. Designating the hotter object as the system and invoking the definition of entropy yields the following:
ΔSsys =
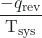 and ΔSsurr =
and ΔSsurr = 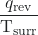
The arithmetic signs of qrev denote the loss of heat by the system and the gain of heat by the surroundings. Since Tsys > Tsurr in this scenario, the magnitude of the entropy change for the surroundings will be greater than that for the system, and so the sum of ΔSsys and ΔSsurr will yield a positive value for ΔSuniv. This process involves an increase in the entropy of the universe.
- The objects are at different temperatures, and heat flows from the cooler to the hotter object. This is never observed to occur spontaneously. Again designating the hotter object as the system and invoking the definition of entropy yields the following:
ΔSsys =
 and ΔSsurr =
and ΔSsurr = 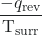
The arithmetic signs of qrev denote the gain of heat by the system and the loss of heat by the surroundings. The magnitude of the entropy change for the surroundings will again be greater than that for the system, but in this case, the signs of the heat changes will yield a negative value for ΔSuniv. This process involves a decrease in the entropy of the universe.
- The temperature difference between the objects is infinitesimally small, Tsys ≈ Tsurr, and so the heat flow is thermodynamically reversible. In this case, the system and surroundings experience entropy changes that are equal in magnitude and therefore sum to yield a value of zero for ΔSuniv. This process involves no change in the entropy of the universe.
These results lead to a profound statement regarding the relation between entropy and spontaneity known as the second law of thermodynamics: all spontaneous changes cause an increase in the entropy of the universe. A summary of these three relations is provided in Table 1.
| ΔSuniv > 0 | spontaneous |
| ΔSuniv < 0 | nonspontaneous (spontaneous in opposite direction) |
| ΔSuniv = 0 | reversible (system is at equilibrium) |
For many realistic applications, the surroundings are vast in comparison to the system. In such cases, the heat gained or lost by the surroundings represents a very small, nearly infinitesimal, fraction of its total thermal energy. For example, combustion of a fuel in air involves transfer of heat from a system (the fuel and oxygen molecules reactants) to surroundings that are infinitely more massive (the earth’s atmosphere). As a result, qsurr is a good approximation of qrev, and the second law may be stated as the following:
ΔSuniv = ΔSsys + ΔSsurr = ΔSsys + ![]()
We may use this equation to predict the spontaneity of a process as illustrated in Example 1.
Example 1
Will Ice Spontaneously Melt?
The entropy change for the process
H2O(s) → H2O(ℓ)
is 22.1 J/K and requires that the surroundings transfer 6.00 kJ of heat to the system. Is the process spontaneous at -10.00 °C? Is it spontaneous at +10.00 °C?
Solution
We can calculate the spontaneity of the process by calculating the entropy change of the universe. If ΔSuniv is positive, then the process is spontaneous. At both temperatures, ΔSsys = 22.1 J/K and qsurr = -6.00 kJ.
At -10.00 °C (263.15 K), the following is true:
ΔSuniv = ΔSsys + ΔSsurr = ΔSsys + ![]() = 22.1 J/K +
= 22.1 J/K + ![]() = -0.7 J/K
= -0.7 J/K
Suniv < 0, so melting is nonspontaneous (not spontaneous) at -10.0 °C.
At 10.00 °C (283.15 K), the following is true:
ΔSuniv = ΔSsys + ![]() = 22.1 J/K +
= 22.1 J/K + ![]() = +0.9 J/K
= +0.9 J/K
Suniv > 0, so melting is spontaneous at 10.00 °C.
Check Your Learning
Using this information, determine if liquid water will spontaneously freeze at the same temperatures. What can you say about the values of Suniv?
Answer:
Entropy is a state function, and freezing is the opposite of melting. At -10.00 °C spontaneous, +0.7 J/K; at +10.00 °C nonspontaneous, -0.9 J/K.
We can understand the relationship between entropy and enthalpy by recalling the equation just before Example 1:
ΔSuniv = ΔSsys + ![]()
The first law requires that qsurr = −qsys, and at constant pressure qsys = ΔH, and so this expression may be rewritten as the following:
ΔSuniv = ΔSsys + ![]() = ΔSsys –
= ΔSsys – ![]() = ΔSsys –
= ΔSsys – ![]()
We will use this relationship again in the next section.
The Third Law of Thermodynamics
The previous section described the various contributions of matter and energy dispersal that contribute to the entropy of a system. With these contributions in mind, consider the entropy of a pure, perfectly crystalline solid possessing no kinetic energy (that is, at a temperature of absolute zero, 0 K). This system may be described by a single microstate, as its purity, perfect crystallinity and complete lack of motion means there is only one possible location for each atom or molecule comprising the crystal, giving the system a single microstate (W = 1). According to the Boltzmann equation, the entropy of this system is zero.
S = k ln(W) = k ln(1) = 0
This limiting condition for a system’s entropy represents the third law of thermodynamics: the entropy of a pure, perfect crystalline substance at 0 K is zero.
Standard Entropies
We can make careful calorimetric measurements to determine the temperature dependence of a substance’s entropy and to derive absolute entropy values under specific conditions. Standard entropies are given the label Sº298 for values determined for one mole of substance at a pressure of 1 bar and a temperature of 298 K. The standard entropy change (ΔS°) for any process may be computed from the standard entropies of its reactant and product species like the following:
ΔSº = ∑(coefficient of product)Sº298(products) – ∑(coefficient of reactant)Sº298(reactants)
For example, ΔS° for the following reaction at room temperature:
mA + nB → xC + yD
is computed as the following:
ΔS° = [xSº298(C) + ySº298(D)] – [mSº298(A) + nSº298(B)]
Table 2 lists some standard entropies at 298.15 K. You can find additional standard entropies in Appendix F.
| Substance | Sº298 (J/mol·K) | Substance | Sº298 (J/mol·K) |
| C(s, graphite) | 5.740 | H2(g) | 130.7 |
| C(s, diamond) | 2.377 | H(g) | 114.7 |
| CO(g) | 197.7 | H2O(g) | 188.8 |
| CO2(g) | 213.7 | H2O(ℓ) | 69.91 |
| CH4(g) | 186.3 | HCl(g) | 186.9 |
| C2H4(g) | 219.6 | H2S(g) | 205.8 |
| C2H6(g) | 229.6 | O2(g) | 205.1 |
| CH3OH(ℓ) | 126.8 | ||
| C2H5OH(ℓ) | 160.7 |
Example 2
Determination of ΔS°
Calculate the standard entropy change for the following process:
H2O(g) → H2O(ℓ)
Solution
The value of the standard entropy change at room temperature, ΔSº298, is the difference between the standard entropy of the product, H2O(ℓ), and the standard entropy of the reactant, H2O(g).
ΔSº = Sº298(H2O(ℓ)) – Sº298(H2O(g)) = (69.91 ![]() ) – (188.83
) – (188.83 ![]() ) = -118.9
) = -118.9 ![]()
The value for ΔSº298 is negative, as expected for this phase transition (condensation), which the previous section discussed.
Check Your Learning
Calculate the standard entropy change for the following process:
H2(g) + C2H4(g) → C2H6(g)
Answer:
−120.6 J/mol·K
Example 3
Determination of ΔS°
Calculate the standard entropy change for the combustion of methanol, CH3OH:
2 CH3OH(ℓ) + 3 O2(g) → 2 CO2(g) + 4 H2O(ℓ)
Solution
The value of the standard entropy change is equal to the difference between the standard entropies of the products and the entropies of the reactants scaled by their stoichiometric coefficients.
ΔSº = [2×Sº298(CO2(g)) + 4×Sº298(H2O(ℓ))] – [2×Sº298(CH3OH(ℓ)) + 3×Sº298(O2(g))]
= [2(213.7 ![]() ) + 4(69.91
) + 4(69.91 ![]() )] – [2(126.8
)] – [2(126.8 ![]() ) + 3(205.1
) + 3(205.1 ![]() )] = -161.9
)] = -161.9 ![]()
Check Your Learning
Calculate the standard entropy change for the following reaction:
Ca(OH)2(s) → CaO(s) + H2O(ℓ)
Answer:
26.27 J/mol·K
Key Concepts and Summary
The second law of thermodynamics states that all spontaneous changes cause an increase in the entropy of the universe. These changes are temperature dependent, which is especially highlighted by the third law of thermodynamics (the entropy of a pure, perfect crystalline substance at 0 K is zero). Using standard conditions and entropies, we can calculate the change in entropy of any process by subtracting the entropy of the reactants from the entropy of the products.
Key Equations
- ΔSuniv = ΔSsys + ΔSsurr
- ΔSuniv = ΔSsys +

- ΔSuniv = ΔSsys –
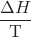
- ΔS° = [xSº298(C) + ySº298(D)] – [mSº298(A) + nSº298(B)] (for mA + nB → xC + yD)
Glossary
- second law of thermodynamics
- all spontaneous changes cause an increase in the entropy of the universe
- standard entropies
- values determined for one mole of a substance at a pressure of 1 bar and a temperature of 298 K (Sº298)
- third law of thermodynamics
- the entropy of a pure, perfect crystalline substance at 0 K is zero
Chemistry End of Section Exercises
- Pure acetic acid melts at 16.6°C at 760 Torr. The molar enthaply of fusion for this process is 11.53 kJ/mol. What is the molar entropy of the system for this process. Is this enough information to determine if the process will occur spontaneously?
- Xylitol is sometimes used as a sugar substitute. It has a melting point of 92.0°C and and heat of fusion of 37.4 kJ/mol. Consider the process of xylitol melting at 362 K and 1.00 atm:
- Predict whether ΔSuniverse will be positive, negative or zero at 362 K and 1 atm, without calculations.
- Calculate the entropy change of the system at 362 K and 1 atm.
- Calculate the entropy change of the surroundings at 362 K and 1 atm.
- Calculate the entropy change of the universe at 362 K and 1 atm. Does this agree with your prediction in part a?
- Using Appendix F, calculate ΔS° at 298 K for the following changes:
- SnCl4(ℓ) → SnCl4(g)
- CS2(g) → CS2(ℓ)
- 2 H2(g) + O2(g) → 2 H2O(ℓ)
- 2 HCl(g) + Pb(s) → PbCl2(s) + H2(g)
- Determine the entropy change for the combustion of gaseous propane, C3H8, under standard state conditions to give gaseous carbon dioxide and water.
- Which of the following statements is/are correct? Select all that apply.
- S°(N2(g) at 25°C) > S° (NO(g) at 25°C) > S° (NO2(g) at 25°C)
- S° (N2 at 1000 K) > S° (N2 at 500 K) > S°(N2 at 298 K)
- S° (ice) > S° (water vapor) > S° (liquid water)
- Aluminum forms a layer of aluminum oxide when exposed to air, which protects the bulk metal from further corrosion:
4 Al(s) + 3 O2(g) → 2 Al2O3(s)
Using the thermodynamic data provided, calculate ΔS° for this reaction.
Species S° (J/mol∙K) Al(s) 28.3 O2(g) 205.0 Al2O3(s) 50.99
Answers to Chemistry End of Section Exercises
- ΔS°rxn = 39.79 J/mol·K; Since it is the entropy of the universe that determines spontaneity, this is not enough information on its own to determine whether the process will occur spontaneously. The entropy of the surrounding must also be known.
- (a) The temperature, 362 K (89°C), is less than the melting point of xylitol so the xylitol will not melt spontaneously and ΔSuniverse is negative.
(b) 102 J/mol·K
(c) -103 J/mol·K
(d) -1 J/mol·K - (a) 107.2 J/mol·K
(b) -86.50 J/mol·K
(c) -326.7 J/mol·K
(d) -171.9 J/mol·K - 100.9 J/mol·K
- B
- -626.2 J/mol∙K
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

