M6Q3: First Law of Thermodynamics and Work

Introduction

The section explores the first law of thermodynamics and work. This section includes worked examples and a glossary.

First Law of Thermodynamics

Substances act as reservoirs of energy by storing energy in the translations, vibrations, and rotations of the molecules (kinetic energy) and in chemical bonds (chemical potential energy). The total energy is often called the internal energy (E), sometimes symbolized as U. The internal energy of a substance is increased when the kinetic energy of its atoms or molecules is raised or its chemical potential energy is increased. The greater kinetic energy may be in the form of increased translations (travel or straight-line motions), vibrations, or rotations of the atoms or molecules. When thermal energy is lost, the kinetic energy of these motions decreases.

The transfer of energy between substances is not categorized as kinetic or potential (which are properties of the molecules and not energy transfer). Instead, energy transfer is characterized as work (w) or heat (q) between system and surroundings. We discussed heat in the previous section—it is the transfer of energy by myriad random collisions between molecules. Work differs from heat by the way that collisions between molecules are harnessed, as discussed below for a piston to produce directed motion. Formally, work is the process of causing matter to move over a distance. A simplified view of work states that a change in volume must occur and is expressed from the system’s point of view with the equation:

w  =  -PΔV

Here, P refers to pressure. The negative sign is necessary to catalog energy transfer from the system’s point of view:  w < 0 when the volume expands (ΔV > 0) and energy is transferred out of the system into the surroundings. If the volume instead decreases (compression, ΔV < 0), then w > 0 and energy is added to the system.

One simple system is the sublimation of solid carbon dioxide to form gaseous carbon dioxide.

CO₂(s)  ⟶  CO₂(g)

If the solid CO₂ is placed in a sealed zip-lock bag and a book is placed on top of it, then work can be done by the system to lift the book as the CO₂(s) sublimates. The system includes everything inside the bag: CO₂(s), CO₂(g), and a small amount of air. As the physical change occurs and gas is generated, the bag inflates and the volume increases (ΔV > 0). The system expends energy (w < 0) in order to lift the book.

As a system undergoes a change, its internal energy can change, and energy can be transferred from the system to the surroundings, or from the surroundings to the system. Energy is transferred into a system when it absorbs heat (q) from the surroundings or when the surroundings do work (w) on the system. For example, energy is transferred into room-temperature metal wire if it is immersed in hot water (the wire absorbs heat from the water), or if you rapidly bend the wire back and forth (the wire becomes warmer because of the work done on it). Both processes increase the internal energy of the wire, which is reflected in an increase in the wire’s temperature. Conversely, energy is transferred out of a system when heat is lost from the system, or when the system does work on the surroundings.

The relationship between internal energy, heat, and work can be represented by the equation:

ΔE = q + w

as shown in Figure 1. This is one version of the first law of thermodynamics, and it shows that the internal energy of a system changes through heat flow into (or out of) the system or work done on (or by) the system. Remember, heat is positive (q > 0) when heat flows into the system; heat is negative (q < 0) when heat flows out of the system. Also, work is positive (w > 0) when work is done on the system; work is negative (w < 0) when work is done by the system.

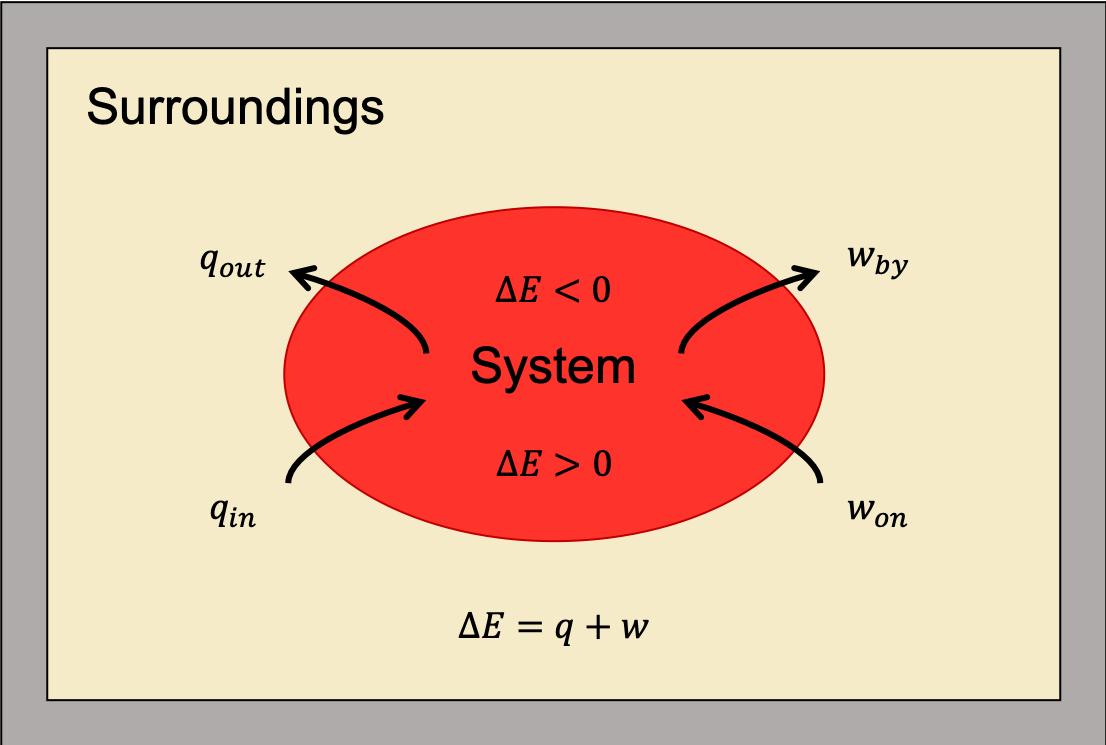
The first law of thermodynamics is a statement of the conservation of energy. Heat is a transfer of energy through the random molecular collisions at the surface where the system and surroundings come into contact. In contrast, work is the transfer of energy through directed motions.

A useful analogy to help you understand the connection between E, ΔE,  q, and w is to think of money and your bank balance (the system). You can reduce your bank balance by visiting an ATM and withdrawing money (analogous to -q and an exothermic change).  You would expect your bank balance to decrease and ΔE would be negative. Withdrawing cash is not the only way to reduce your bank balance. Making a purchase using a debit card (analogous to w) would also reduce E. However, making a deposit at an ATM would be analogous to +q and an endothermic change, and ΔE would be positive. In fact, if you deposit $100 you would expect your bank balance to increase by exactly $100 – the Law of Conservation of Money!

Harnessing Heat: Work and the Movable Wall

Our modern society is built on turning chemical potential energy into work and the movement of pistons, such as in our cars. The operation of an internal combustion engine harnesses the energy released when burning fuel to move pistons and propel a car forward. The reaction of gasoline and oxygen is exothermic. Some of this energy is given off as heat, and some does work pushing the piston in the cylinder. The substances involved in the reaction are the system, and the engine and the rest of the universe are the surroundings. The system loses energy by both heating and doing work on the surroundings, and its internal energy decreases. (The engine is able to keep the car moving because this process is repeated many times per second while the engine is running.)

Constant Pressure versus Constant Volume Systems

Let us compare the two ways that we can increase the energy of a system consisting of heating water contained in a cylinder. In both cases, as heat is added to the system, the water is converted from liquid to gaseous form. The added heat increases the kinetic energy of water molecules and eventually disrupts the hydrogen-bonds between water molecules to boil the water.

H₂O(ℓ) + energy  ⟶  H₂O(g)

In a constant pressure system, the volume of gas above the liquid can change to maintain a constant pressure (i.e., atmospheric pressure) (Figure 2). As heat is added, the water boils and the amount of H₂O(g) increases. The piston therefore moves up (volume increases, ΔV > 0), and thus w  =  –PΔV < 0. The piston does work on the surroundings! Pistons used in our cars then move a crank shaft, the wheels turn, and the car or train or boat is pushed forward. This partial conversion of heat into work is the basis of much of our modern society. In later classes, you will learn how to calculate just how efficient this conversion is.

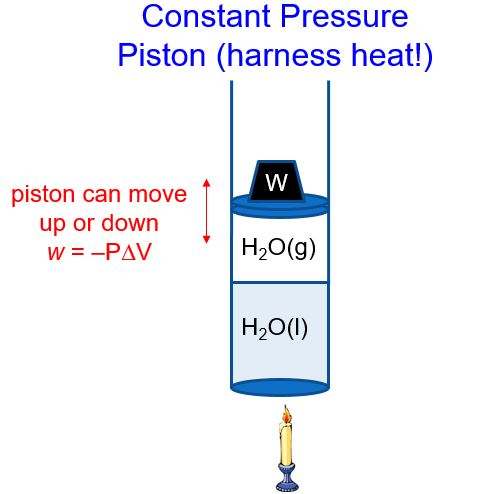
We’ll refer to the heat that flows in or out of a constant pressure system as q_p. If we rearrange the first law of thermodynamics, ΔE = q_p + w and substitute in w = -PΔV, we get:

ΔE = q_p – PΔV

solving for heat (q_p):

q_p = ΔE + PΔV

q_p is the change in enthalpy, ΔH. The word enthalpy means “to warm”.  We can therefore write ΔH = ΔE + PΔV.  We’ll explore this very important concept of enthalpy in greater detail later in the module.

In a constant volume system, the volume of gas above the liquid cannot change (Figure 3). As heat is added and the amount of gas increases, the piston cannot move up. Thus, no work can be done by the system.

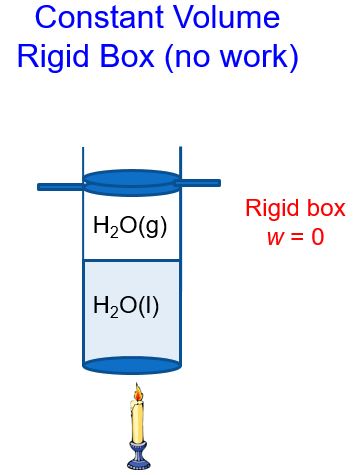
We’ll refer to the heat in a constant volume system as q_v. If we use the first law of thermodynamics, ΔE = q + w and substitute in w = 0 at constant volume and solve for heat q = q_v, we get:

ΔE = q_v

Comparing the two systems (constant pressure and constant volume) shows an important difference between internal energy (ΔE) and enthalpy (ΔH). The difference between internal energy and enthalpy is the work that a piston can do at constant pressure.

To summarize, for a thermodynamic experiment performed under constant pressure, any volume expansion by the production of a gas will result in work being expended by the system. If we are interested in only knowing the enthalpy change for the system (ΔH) then it will be exactly the same as the heat input into the system, q_p. However, if we wanted to know the total internal energy change (ΔE) for the system we would have to know the amount of work performed as well. In chemistry where the focus is on the chemical reaction we rarely do this as w is relatively small compared to q_p, even when a significant amount of gas is produced. Looking ahead we will be calculating enthalpy changes for chemical reactions (system) by measuring q_p in calorimetry experiments performed in an open system (coffee cup calorimeter) at constant pressure. Other calorimeters (bomb calorimeter) are closed systems and operate at constant volume. Calorimetry experiments using bomb calorimeters measure q_v, and therefore allow a direct determination of ΔE for the chemical reaction (system).

Key Concepts and Summary

Heat and work are two modes of energy transfer between system and surroundings. Heat is the transfer of energy by random molecular collisions and work harnesses these collisions to create directed motions, such as in a piston (a moveable wall). The sum of heat and work is the change in energy of the system:  ΔE = q + w. This is called the first law of thermodynamics. The partial conversion of heat into useful work by an engine (to run electric generators or cars or trains or boats or airplanes) is the basis of our modern industrial society. As we discussed earlier in the semester, the creation of heat by combustion also releases CO₂ into the atmosphere, leading to climate change.

Key Equations

• ΔE = q + w
• ΔH = ΔE + PΔV
• ΔH = q_p
• ΔE = q_v

Glossary

chemical thermodynamics

area of science that deals with the relationships between heat, work, and all forms of energy associated with chemical and physical processes

enthalpy (H)

is an energy like internal energy (E). The important attribute of H is that ΔH  =  q_p, the heat transferred at constant pressure.

expansion work (pressure-volume work)

work done as a system expands or contracts against external pressure

first law of thermodynamics

internal energy of a system changes due to heat flow in or out of the system or work done on or by the system

internal energy (E)

sum of all kinetic and potential energies of the molecules in the system. It is the change in E that is useful to understand, and it is expressed through the first law of thermodynamics, ΔE  =  q + w.