M4Q1: Moles, AMUs, and Conversions

Introduction

The section explores how we convert between the three different ways of representing amounts of chemical substances, i.e., mass, moles and number of submicroscopic particles (atoms, molecules ions) using molar masses and Avogadro’s number. How to determine the mass percentage of each element in a chemical compound from its chemical formula is also outlined. This section includes worked examples, sample problems, and a glossary.

Learning Objectives for Moles, AMUs, and Conversions

| Key Concepts and Summary | Key Equations | Glossary | End of Section Exercises |

We can argue that modern chemical science began when scientists started exploring the quantitative as well as the qualitative aspects of chemistry. For example, Dalton’s atomic theory was an attempt to explain the results of measurements that allowed him to calculate the relative masses of elements combined in various compounds. Understanding the relationship between the masses of atoms and the chemical formulas of compounds allows us to quantitatively describe the composition of substances.

Formula Mass

In an earlier module, we described the development of the atomic mass unit, the concept of average atomic masses, and the use of chemical formulas to represent the elemental makeup of substances. These ideas can be extended to calculate the formula mass of a substance by summing the average atomic masses of all the atoms represented in the substance’s formula.

Formula mass for covalent substances

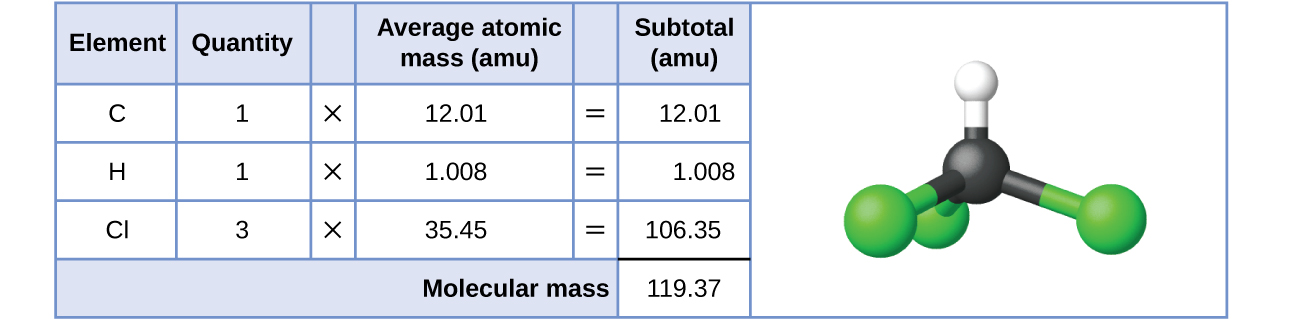
For covalent substances, the formula represents the numbers and types of atoms composing a single molecule of the substance; therefore, the formula mass may be correctly referred to as a molecular mass. Consider chloroform (CHCl3), a covalent compound once used as a surgical anesthetic and now primarily used in the production of the “anti-stick” polymer, Teflon. The molecular formula of chloroform indicates that a single molecule contains one carbon atom, one hydrogen atom, and three chlorine atoms. The average molecular mass of a chloroform molecule is therefore equal to the sum of the average atomic masses of these atoms. Figure 1 outlines the calculations used to derive the molecular mass of chloroform, which is 119.37 amu.

A table and diagram are shown. The table is made up of six columns and five rows. The header row reads: “Element,” “Quantity,” a blank space, “Average atomic mass (a m u),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “C,” “H,” “C l” and a blank, merged cell that runs the width of the first five columns. The second column contains the numbers “1,” “1,” and “3” as well as the merged cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “12.01,” “1.008,” and “35.45” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values “12.01,” “1.008,” “106.35,” and “119.37.” There is a thick black line below the number 106.35. The merged cell under the first five columns reads “Molecular mass.” To the left of the table is a diagram of a molecule. Three green spheres are attached to a slightly smaller black sphere, which is also attached to a smaller white sphere. The green spheres lie beneath and to the sides of the black sphere while the white sphere is located straight up from the black sphere.
Figure 1. The average mass of a chloroform molecule, CHCl3, is 119.37 amu, which is the sum of the average atomic masses of each of its constituent atoms. The model shows the molecular structure of chloroform.

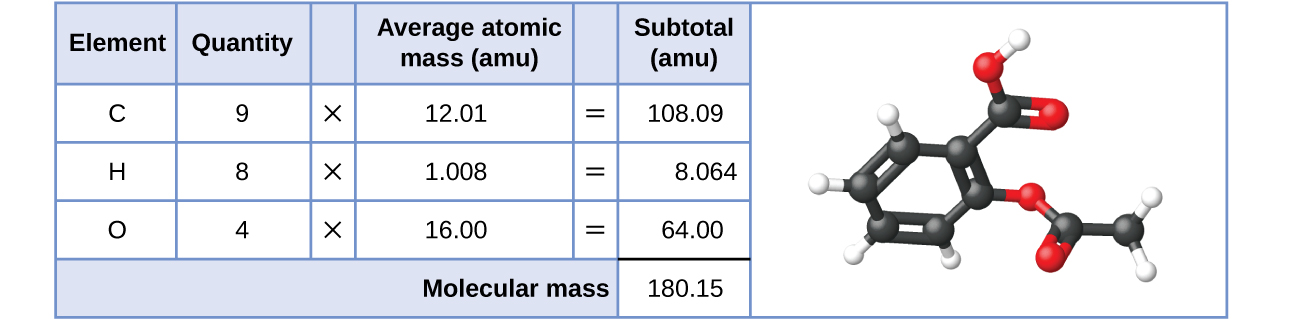
Likewise, the molecular mass of an aspirin molecule, C9H8O4, is the sum of the atomic masses of nine carbon atoms, eight hydrogen atoms, and four oxygen atoms, which amounts to 180.15 amu (Figure 2).

A table and diagram are shown. The table is made up of six columns and five rows. The header row reads: “Element,” “Quantity,” a blank space, “Average atomic mass (a m u),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “C,” “H,” “O,” and a merged cell. The merged cell runs the length of the first five columns. The second column contains the numbers “9,” “8,” and “4” as well as the merged, cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “12.01,” “1.008,” and “16.00” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values: “108.09,” “8.064,” “64.00,” and “180.15.” There is a thick black line below the number 64.00. The merged cell under the first five columns reads “Molecular mass.” To the left of the table is a diagram of a molecule. Six black spheres are located in a six-sided ring and connected by alternating double and single black bonds. Attached to each of the four black spheres is one smaller white sphere. Attached to the farthest right black sphere is a red sphere, connected to two more black spheres, all in a row. Attached to the last black sphere of that row are two more white spheres. Attached to the first black sphere of that row is another red sphere. A black sphere, attached to two red spheres and a white sphere is attached to the black sphere on the top right of the six-sided ring.
Figure 2. The average mass of an aspirin molecule is 180.15 amu. The model shows the molecular structure of aspirin, C9H8O4.

Example 1

Computing Molecular Mass for a Covalent Compound
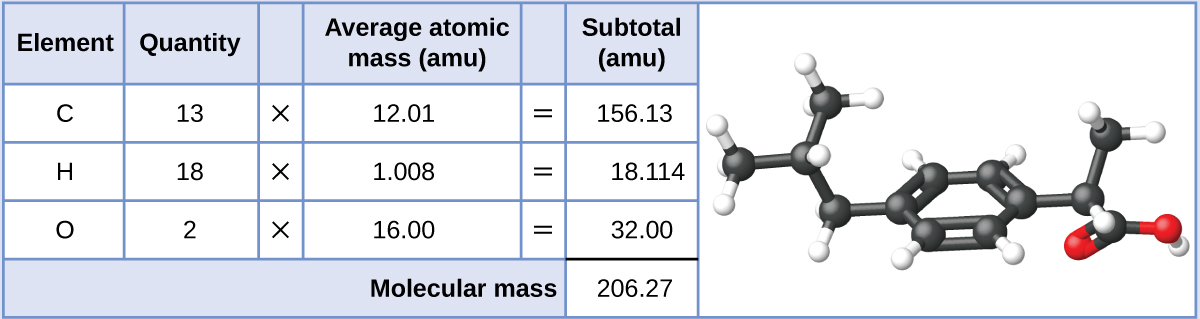
Ibuprofen, C13H18O2, is a covalent compound and the active ingredient in several popular nonprescription pain medications, such as Advil and Motrin. What is the molecular mass (amu) for this compound?

Solution
Molecules of this compound are comprised of 13 carbon atoms, 18 hydrogen atoms, and 2 oxygen atoms. Following the approach described above, the average molecular mass for this compound is therefore:

A table is shown that is made up of six columns and five rows. The header row reads: “Element,” “Quantity,” a blank space, “Average atomic mass (a m u),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “C,” “H,” “O,” and a merged cell. The merged cell runs the length of the first five columns. The second column contains the numbers “13,” “8,” and “2” as well as the merged cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “12.01,” “1.008,” and “16.00” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values “156.13,” “18.114,” “32.00,” and “206.27.” There is a thick black line below the number 32.00. The merged cell under the first five columns reads “Molecular mass.” To the right is a ball-and-stick model of the structure. At the center, it shows six black spheres arranged in a six-sided ring with alternating double bonds. The two black spheres at the top and bottom of the six-sided ring are each bonded to one, smaller, white sphere. The black sphere on the left side of the six-sided ring is connect to another black sphere. This sphere is connected to two smaller, white spheres and another black sphere. This black sphere is connected to one, smaller white sphere, and two other black spheres. Each of these last two black spheres is connected to two smaller, white spheres. The black sphere on the right side of the six-sided ring is connected to another black sphere. This black sphere is connected to one smaller, white sphere and two other black spheres. The black sphere that is connected to it and is situated to the top right is connected to two smaller, white spheres. The black sphere connected towards the bottom right is connected to two red spheres. It forms a double bond with one of these red spheres and the other red sphere is connected to a smaller, white sphere.

Check Your Learning
Acetaminophen, C8H9NO2, is a covalent compound and the active ingredient in several popular nonprescription pain medications, such as Tylenol. What is the molecular mass (amu) for this compound?

Answer:

151.16 amu

Formula mass for ionic compounds

Ionic compounds are composed of discrete cations and anions combined in ratios to yield electrically neutral bulk matter. The formula mass for an ionic compound is calculated in the same way as the formula mass for covalent compounds: by summing the average atomic masses of all the atoms in the compound’s formula. Keep in mind that the formula for an ionic compound does not represent the composition of a discrete molecule, so it may not correctly be referred to as the “molecular mass.”

As an example, consider sodium chloride, NaCl, the chemical name for common table salt. Sodium chloride is an ionic compound composed of sodium cations, Na+, and chloride anions, Cl−, combined in a 1:1 ratio. The formula mass for this compound is computed as 58.44 amu (see Figure 3).

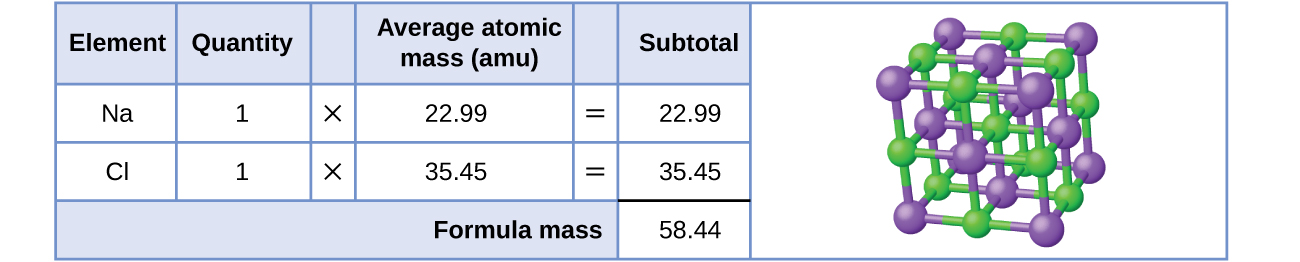
A table and diagram are shown. The table is made up of six columns and four rows. The header row reads: “Element,” “Quantity,” a blank space, “Average atomic mass (a m u),” a blank space and “Subtotal (a m u).” The first column contains the symbols “N a”, “C l,” and a merged cell. The merged cell runs the length of the first five columns. The second column contains the numbers “1” and “1” as well as the merged cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “22.99” and “35.45” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values “22.99,” “35.45,” and “58.44.” There is a thick black line below the number “35.45.” The merged cell under the first five columns reads “Formula mass.” To the left of the table is a diagram of a chemical structure. The diagram shows green and purple spheres placed in an alternating pattern, making up the corners of eight stacked cubes to form one larger cube. The green spheres are slightly smaller than the purple spheres.
Figure 3. Table salt, NaCl, contains an array of sodium and chloride ions combined in a 1:1 ratio. Its formula mass is 58.44 amu.

Note that the average masses of neutral sodium and chlorine atoms were used in this computation, rather than the masses for sodium cations and chlorine anions. This approach is perfectly acceptable when computing the formula mass of an ionic compound. Even though a sodium cation has a slightly smaller mass than a sodium atom (since it is missing an electron), this difference will be offset by the fact that a chloride anion is slightly more massive than a chloride atom (due to the extra electron). Moreover, the mass of an electron is negligibly small with respect to the mass of a typical atom. Even when calculating the mass of an isolated ion, the missing or additional electrons can generally be ignored, since their contribution to the overall mass is negligible, reflected only in the nonsignificant digits that will be lost when the computed mass is properly rounded. The few exceptions to this guideline are very light ions derived from elements with precisely known atomic masses.

Example 2

Computing Formula Mass for an Ionic Compound
Aluminum sulfate, Al2(SO4)3, is an ionic compound that is used in the manufacture of paper and in various water purification processes. What is the formula mass (amu) of this compound?

Solution
The formula for this compound indicates it contains Al3+ and SO42− ions combined in a 2:3 ratio. For purposes of computing a formula mass, it is helpful to rewrite the formula in the simpler format, Al2S3O12. Following the approach outlined above, the formula mass for this compound is calculated as follows:

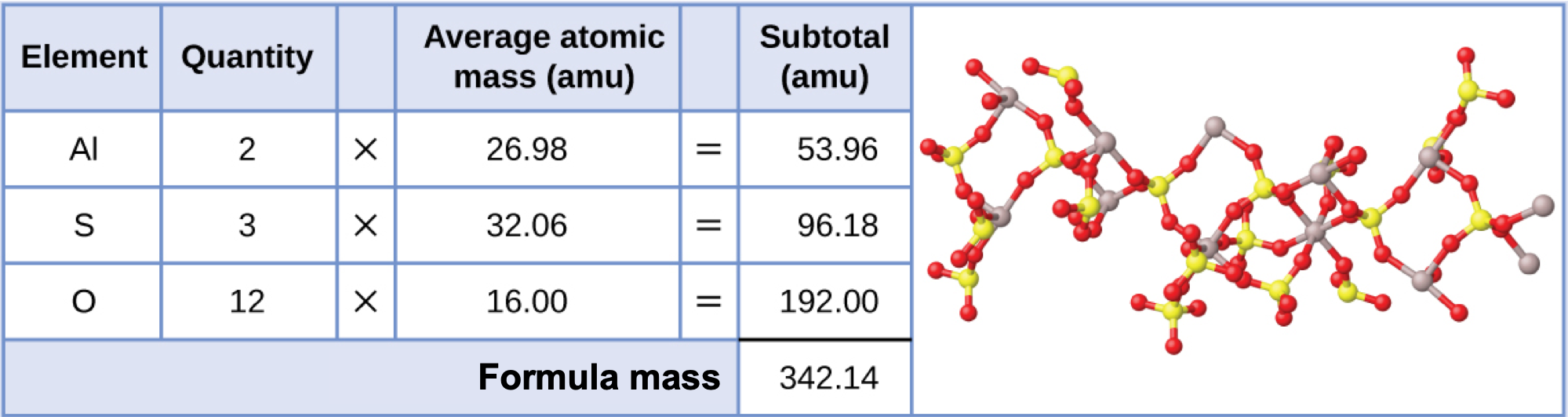
A table is shown that is made up of six columns and five rows. The header row reads: “Element,” “Quantity,” a blank space, “Average atomic mass (a m u),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “A l,” “S,” “O,” and a merged cell. The merged cell runs the length of the first five columns. The second column contains the numbers “2,” “3,” and “12” as well as the merged cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “26.98,” “32.06,” and “16.00” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values “53.96,” “96.18,” “192.00,” and “342.14.” There is a thick black line under the number 192.00. The merged cell under the first five columns reads “Molecular mass.” To the right of this table is a ball-and-stick structure. It shows yellow and grey sphere connected to red spheres in a complex pattern. The yellow and grey spheres are similar in size, but the red spheres appear to be smaller by comparison.

Check Your Learning
Calcium phosphate, Ca3(PO4)2, is an ionic compound and a common anti-caking agent added to food products. What is the formula mass (amu) of calcium phosphate?

Answer:

310.18 amu

The Mole

The identity of a substance is defined not only by the types of atoms or ions it contains, but by the quantity of each type of atom or ion. For example, water, H2O, and hydrogen peroxide, H2O2, are alike in that their respective molecules are composed of hydrogen and oxygen atoms. However, because a hydrogen peroxide molecule contains two oxygen atoms, as opposed to the water molecule, which has only one, the two substances exhibit very different properties. Today, we possess sophisticated instruments that allow the direct measurement of these defining microscopic traits; however, the same traits were originally derived from the measurement of macroscopic properties (the masses and volumes of bulk quantities of matter) using relatively simple tools (balances and volumetric glassware). This experimental approach required the introduction of a new unit for amount of substances, the mole, which remains indispensable in modern chemical science.

The mole is an amount unit similar to familiar units like pair, dozen, gross, etc. It provides a specific measure of the number of atoms or molecules in a bulk sample of matter. Until 2019, the definition of a mole was the amount of substance containing the same number of discrete entities (such as atoms, molecules, and ions) as the number of atoms in a sample of pure 12C with a mass of exactly 12 g. One Latin connotation for the word “mole” is “large mass” or “bulk,” which is consistent with its use as the name for this unit. The mole provides a link between an easily measured macroscopic property—bulk mass—and an extremely important fundamental property—number of atoms, molecules, and so forth.

The number of entities composing a mole has been experimentally determined to be 6.022141 × 1023. Since the 2019 redefinition, one mole is now defined as containing exactly 6.02214076 × 1023 elementary entities. This value is a fundamental constant named Avogadro’s number (NA) (or the Avogadro constant) in honor of Italian scientist Amedeo Avogadro. This constant is properly reported with an explicit unit of “per mole,” a typical rounded version being 6.022 × 1023/mol. The unit “per mole” may seem strange, but compare it to “per dozen” where there are 12/dozen (e.g., 12 cookies/dozen cookies, 12 pencils/dozen pencils, 12 entities/dozen entities, etc.). There are 6.022 × 1023 entities per mole.

Consistent with its definition as an amount unit, 1 mole of any element contains the same number of atoms as 1 mole of any other element. The masses of 1 mole of different elements, however, are different, since the masses of the individual atoms are drastically different. The molar mass of an element (or compound) is the mass in grams of 1 mole of that substance, a property expressed in units of grams per mole (g/mol) (see Figure 4).

This figure contains eight different substances displayed on white circles. The amount of each substance is visibly different.
Figure 4. Each sample contains 6.022 × 1023 atoms —1.00 mol of atoms. From left to right (top row): 65.4 g zinc, 12.0 g carbon, 24.3 g magnesium, and 63.5 g copper. From left to right (bottom row): 32.1 g sulfur, 28.1 g silicon, 207 g lead, and 118.7 g tin. (credit: modification of work by Mark Ott)

Because the definition of the mole used to be based on the same reference substance as the definition of the atomic mass unit, i.e., 12C, the molar mass of any substance is numerically equivalent to its atomic or formula mass in amu. In other words, a single 12C atom has an atomic mass of 12 amu, and 1 mole of 12C atoms (its molar mass) is 12 g/mol. This relationship holds for all elements. Extending this principle, the molar mass of a compound in grams is likewise numerically equivalent to its formula mass in amu (Figure 5).

This photo shows two vials filled with a colorless liquid. It also shows two bowls: one filled with an off-white powder and one filled with a bright red powder.
Figure 5. Each sample contains 6.02 × 1023 molecules or formula units—1.00 mol of the compound or element. Clock-wise from the upper left: 130.2 g of C8H17OH (1-octanol, formula mass 130.2 amu), 454.4 g of HgI2 (mercury(II) iodide, formula mass 454.4 amu), 32.0 g of CH3OH (methanol, formula mass 32.0 amu) and 256.5 g of S8 (sulfur, formula mass 256.5 amu). (credit: Sahar Atwa)
Element Average Atomic Mass (amu) Molar Mass (g/mol) Atoms/Mole
C 12.01 12.01 6.022 × 1023
H 1.008 1.008 6.022 × 1023
O 16.00 16.00 6.022 × 1023
Na 22.99 22.99 6.022 × 1023
Cl 35.45 35.45 6.022 × 1023

While atomic mass and molar mass are numerically equivalent, keep in mind that they are vastly different in terms of scale, as represented by the vast difference in the magnitudes of their respective units (amu versus g). To appreciate the enormity of the mole, consider a small drop of water with a mass about 0.03 g (see Figure 6). Although this represents just a tiny fraction of 1 mole of water (which has a mass of ~18 g), it contains more water molecules than can be clearly imagined. If the molecules were distributed equally among the roughly seven billion people on earth, each person would receive more than 100 billion molecules.

A close-up photo of a water droplet on a leaf is shown. The water droplet is not perfectly spherical.
Figure 6. The number of molecules in a single droplet of water is roughly 100 billion times greater than the number of people on earth. (credit: “tanakawho”/Wikimedia commons)

 

The mole is used in chemistry to represent 6.022 × 1023 of something, but it can be difficult to conceptualize such a large number. Watch this video title “How big is a mole?” and then complete the “Think” questions that follow. Explore more about the mole by reviewing the information under “Dig Deeper.”

The relationships between formula mass, the mole, and Avogadro’s number can be applied to compute various quantities that describe the composition of substances and compounds. For example, if we know the mass and chemical composition of a substance, we can determine the number of moles and calculate number of atoms or molecules in the sample. Likewise, if we know the number of moles of a substance, we can derive the number of atoms or molecules and calculate the substance’s mass.

Example 3

Deriving Moles from Grams for an Element
According to nutritional guidelines from the US Department of Agriculture, the estimated average requirement for dietary potassium is 4.7 g. What is the estimated average requirement of potassium in moles?

Solution
The mass of K is provided, and the corresponding amount of K in moles is requested. Referring to the periodic table, the atomic mass of K is 39.10 amu, and so its molar mass is 39.10 g/mol. The given mass of K (4.7 g) is a bit more than one-tenth the molar mass (39.10 g), so a reasonable “ballpark” estimate of the number of moles would be slightly greater than 0.1 mol.

The molar amount of a substance may be calculated by dividing its mass (g) by its molar mass (g/mol):

A diagram of two boxes connected by a right-facing arrow is shown. The box on the left contains the phrase, “Mass of K atoms ( g )” while the one on the right contains the phrase, “Moles of K atoms ( mol ).” There is a phrase under the arrow that says, “Divide by molar mass (g / mol).”

The factor-label method supports this mathematical approach since the unit “g” cancels and the answer has units of “mol:”

4.7 g K × \left(\dfrac{\text{mol K}}{39.10\;\rule[0.25ex]{0.8em}{0.1ex}\hspace{-0.65em}\text{g}}\right) = 0.12 mol K

The calculated magnitude (0.12 mol K) is consistent with our ballpark expectation, since it is a bit greater than 0.1 mol.

Check Your Learning
Beryllium is a light metal used to fabricate transparent X-ray windows for medical imaging instruments. How many moles of Be are in a thin-foil window weighing 3.24 g?

Answer:

0.360 mol

Example 4

Deriving Grams from Moles for an Element
A liter of air contains 9.2 × 10−4 mol argon. What is the mass of Ar in a liter of air?

Solution
The molar amount of Ar is provided and must be used to derive the corresponding mass in grams. Since the amount of Ar is less than 1 mole, the mass will be less than the mass of 1 mole of Ar, approximately 40 g. The molar amount in question is approximately one-one thousandth (~10−3) of a mole, and so the corresponding mass should be roughly one-one thousandth of the molar mass (~0.04 g):

A diagram of two boxes connected by a right-facing arrow is shown. The box on the left contains the phrase, “Moles of A r atoms ( mol )” while the one on the right contains the phrase, “Mass of A r atoms ( g ).” There is a phrase under the arrow that says “Multiply by molar mass ( g / mol ).”

In this case, logic dictates (and the factor-label method supports) multiplying the provided amount (mol) by the molar mass (g/mol):

9.2 × 10-4 mol Ar × \left(\dfrac{39.95\;\text{g}}{\rule[0.5ex]{1.7em}{0.1ex}\hspace{-1.7em}\text{mol} \;\text{Ar}}\right) = 0.037 g Ar

The result is in agreement with our expectations, around 0.04 g Ar.

Check Your Learning
What is the mass of 2.561 mol of gold?

Answer:

504.4 g

Example 5

Deriving Number of Atoms from Mass for an Element
Copper is commonly used to fabricate electrical wire (Figure 7). How many copper atoms are in 5.00 g of copper wire?

A close-up photo of a spool of copper wire is shown.
Figure 7. Copper wire is composed of many, many atoms of Cu. (credit: Emilian Robert Vicol)

Solution
The number of Cu atoms in the wire may be conveniently derived from its mass by a two-step computation: first calculating the molar amount of Cu, and then using Avogadro’s number (NA) to convert this molar amount to number of Cu atoms:

A diagram of three boxes connected by a right-facing arrow in between each is shown. The box on the left contains the phrase, “Mass of C u atoms ( g ),” the middle box reads, “Moles of C u atoms ( mol ),” while the one on the right contains the phrase, “Number of C u atoms.” There is a phrase under the left arrow that says “Divide by molar mass (g / mol),” and under the right arrow it states, “Multiply by Avogadro’s number ( mol superscript negative one ).”

Considering that the provided sample mass (5.00 g) is a little less than one-tenth the mass of 1 mole of Cu (~64 g), a reasonable estimate for the number of atoms in the sample would be on the order of one-tenth NA, or approximately 1022 Cu atoms. Carrying out the two-step computation yields:

5.00 g Cu × \left(\dfrac{\rule[0.5ex]{1.7em}{0.1ex}\hspace{-1.7em}\text{mol} \;\text{Cu}}{63.55\;\rule[0.25ex]{0.8em}{0.1ex}\hspace{-0.65em}\text{g}}\right) \times \left(\dfrac{6.022 \times 10^{23} \;\text{atoms}}{\rule[0.5ex]{1.7em}{0.1ex}\hspace{-1.7em}\text{mol}}\right) = 4.74 × 1022 atoms of copper

The factor-label method yields the desired cancellation of units, and the computed result is on the order of 1022 as expected.

Check Your Learning
A prospector panning for gold in a river collects 15.00 g of pure gold. How many Au atoms are in this quantity of gold?

Answer:

4.586 × 1022 Au atoms

Example 6

Deriving Moles from Grams for a Compound
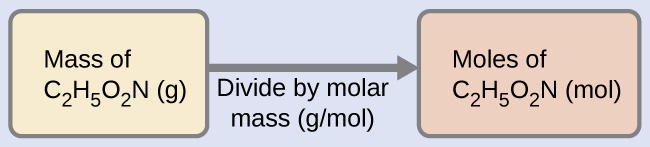
Our bodies synthesize protein from amino acids. One of these amino acids is glycine, which has the molecular formula C2H5O2N. How many moles of glycine molecules are contained in 28.35 g of glycine?

Solution
We can derive the number of moles of a compound from its mass following the same procedure we used for an element in Example 3:

A diagram of two boxes connected by a right-facing arrow is shown. The box on the left contains the phrase, “Mass of C subscript 2 H subscript 5 O subscript 2 N ( g )” while the box on the right contains the phrase, “Moles of C subscript 2 H subscript 5 O subscript 2 N ( mol ).” There is a phrase under the arrow that says “Divide by molar mass (g / mol).”

The molar mass of glycine is required for this calculation, and it is computed in the same fashion as its molecular mass. One mole of glycine, C2H5O2N, contains 2 moles of carbon, 5 moles of hydrogen, 2 moles of oxygen, and 1 mole of nitrogen:

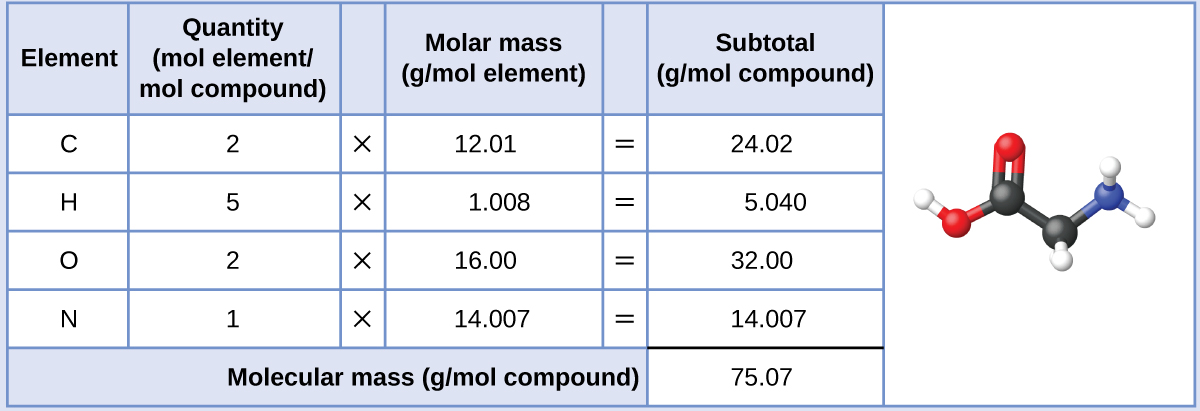
A table is shown that is made up of six columns and six rows. The header row reads: “Element,” “Quantity (mol element / mol compound,” a blank space, “Molar mass (g / mol element),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “C,” “H,” “O,” “N,” and a merged cell. The merged cell runs the width of the first five columns. The second column contains the numbers “2,” “5,” “2,” and “1” as well as the merged cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “12.01,” “1.008,” “16.00,” and “14.007” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values “24.02,” “5.040,” “32.00,” “14.007,” and “75.07.” There is a thick black line under the number 14.007. The merged cell under the first five columns reads “Molar mass (g / mol compound). There is a ball-and-stick drawing to the right of this table. It shows a black sphere that forms a double bond with a slightly smaller red sphere, a single bond with another red sphere, and a single bond with another black sphere. The red sphere that forms a single bond with the black sphere also forms a single bond with a smaller, white sphere. The second black sphere forms a single bond with a smaller, white sphere and a smaller blue sphere. The blue sphere forms a single bond with two smaller, white spheres each.

The provided mass of glycine (~28 g) is a bit more than one-third the molar mass (~75 g/mol), so we would expect the computed result to be a bit greater than one-third of a mole (~0.33 mol). Dividing the compound’s mass by its molar mass yields:

28.35 g glycine × \left(\dfrac{\text{mol glycine}}{75.07 \;\rule[0.25ex]{0.8em}{0.1ex}\hspace{-0.65em}\text{g}}\right) = 0.3776 mol glycine

This result is consistent with our rough estimate.

Check Your Learning
How many moles of sucrose, C12H22O11, are in a 25. g sample of sucrose?

Answer:

0.073 mol

Example 7

Deriving Grams from Moles for a Compound
Vitamin C is a covalent compound with the molecular formula C6H8O6. The recommended daily dietary allowance of vitamin C for children aged 4–8 years is 1.42 × 10−4 mol. What is the mass of this allowance in grams?

Solution
As for elements, the mass of a compound can be derived from its molar amount as shown:

A diagram of two boxes connected by a right-facing arrow is shown. The box on the left contains the phrase, “Moles of vitamin C ( mol )” while the one the right contains the phrase, “Mass of vitamin C ( g )”. There is a phrase under the arrow that says “Multiply by molar mass (g / mol).”

The molar mass for this compound is computed to be 176.124 g/mol. The given number of moles is a very small fraction of a mole (~10−4 or one-ten thousandth); therefore, we would expect the corresponding mass to be about one-ten thousandth of the molar mass (~0.02 g). Performing the calculation, we get:

1.42 × 10-4 mol vitamin C × \left(\dfrac{176.124\;\text{g}}{\rule[0.5ex]{1.7em}{0.1ex}\hspace{-1.7em}\text{mol} \;\text{vitamin C}}\right) = 0.0250 g vitamin C

This is consistent with the anticipated result.

Check Your Learning
What is the mass of 0.443 mol of hydrazine, N2H4?

Answer:

14.2 g

Example 8

Deriving the Number of Atoms and Molecules from the Mass of a Compound
A packet of an artificial sweetener contains 40.0 mg of saccharin (C7H5NO3S), which has the structural formula:

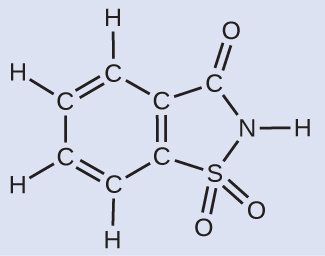
A diagram of a molecule is shown that is made up of two ring structures attached together. The left ring is hexagonal in shape with C atoms at each point of the ring and alternating single and double bonds. A double bond occurs between the C atom at the top vertex of the hexagon and the C atom down and to the left of it. The C atoms on the left, top, and bottom of the structure form a single bond to an H atom each. The two right C atoms make up one side of a pentagon and the other points of the pentagon are made up of a C atom, an N atom, and an S atom if read clockwise. The C atom forms a double bond with an O atom. The N atom forms a single bond with an H atom. The S atom forms two double bonds to two O atoms.

Given that saccharin has a molar mass of 183.18 g/mol, how many saccharin molecules are in a 40.0-mg (0.0400-g) sample of saccharin? How many carbon atoms are in the same sample?

Solution
The number of molecules in a given mass of compound is computed by first deriving the number of moles, as demonstrated in Example 6, and then multiplying by Avogadro’s number:

A diagram of three boxes connected by a right-facing arrow in between each is shown. The box on the left contains the phrase, “Mass of C subscript seven H subscript five N O subscript three S ( g ),” the middle box reads, “Moles of C subscript seven H subscript five N O subscript three S ( mol ),” while the one on the right contains the phrase, “Number of C subscript seven H subscript five N O subscript three S molecules.” There is a phrase under the left arrow that says, “Divide by molar mass (g / mol),” and under the right arrow it states, “Multiply by Avogadro’s number ( mol superscript negative one).”

Using the provided mass and molar mass for saccharin yields:

0.0400\;\rule[0.25ex]{0.8em}{0.1ex}\hspace{-0.65em}\text{g} \;\text{C}_7\text{H}_5\text{NO}_3\text{S} \times \left(\dfrac{\rule[0.5ex]{1.7em}{0.1ex}\hspace{-1.7em}\text{mol} \;\text{C}_7\text{H}_5\text{NO}_3\text{S}}{183.18 \;\rule[0.25ex]{0.8em}{0.1ex}\hspace{-0.65em}\text{g} \;\text{C}_7\text{H}_5\text{NO}_3\text{S}}\right) \times \left(\dfrac{6.022 \times 10^{23} \;\text{C}_7\text{H}_5\text{NO}_3\text{S} \;\text{molecules}}{1\;\rule[0.5ex]{1.7em}{0.1ex}\hspace{-1.7em}\text{mol} \;\text{C}_7\text{H}_5\text{NO}_3\text{S}}\right)

 = 1.31 × 1020 C7H5NO3S molecules

The compound’s formula shows that each molecule contains seven carbon atoms, and so the number of C atoms in the provided sample is:

1.31 × 1020 C7H5NO3S molecules × \left(\dfrac{7 \;\text{C atoms}}{1 \;\text{C}_7\text{H}_5\text{NO}_3\text{S molecule}}\right) = 9.20 × 1020 C atoms

Check Your Learning
How many C4H10 molecules are contained in 9.213 g of this compound? How many hydrogen atoms?

Answer:

9.545 × 1022 molecules C4H10; 9.545 × 1023 atoms H

Above, we discussed the relationship between the bulk mass of a substance and the number of atoms or molecules it contains (moles). Given the chemical formula of the substance, we were able to determine the amount of the substance (moles) from its mass, and vice versa. But what if the chemical formula of a substance is unknown? In this section, we will explore how to apply these very same principles in order to derive the chemical formulas of unknown substances from experimental mass measurements.

Percent Composition

The elemental makeup of a compound defines its chemical identity, and chemical formulas are the most succinct way of representing this elemental makeup. When a compound’s formula is unknown, measuring the mass of each of its constituent elements is often the first step in the process of determining the formula experimentally. The results of these measurements permit the calculation of the compound’s percent composition, defined as the percentage by mass of each element in the compound. For example, consider a gaseous compound composed solely of carbon and hydrogen. The percent composition of this compound could be represented as follows:

% H = \dfrac{\text{mass H}}{\text{mass compound}} × 100%

% C = \dfrac{\text{mass C}}{\text{mass compound}} × 100%

If analysis of a 10.0-g sample of this gas showed it to contain 2.5 g H and 7.5 g C, the percent composition would be calculated to be 25% H and 75% C:

% H = \dfrac{2.5\;\text{g H}}{10.0 \;\text{g compound}} × 100% = 25%

% C = \dfrac{7.5\;\text{g C}}{10.0 \;\text{g compound}} × 100% = 75%

Example 9

Calculation of Percent Composition

Analysis of a 12.04-g sample of a liquid compound composed of carbon, hydrogen, and nitrogen showed it to contain 7.34 g C, 1.85 g H, and 2.85 g N. What is the percent composition of this compound?

Solution
To calculate percent composition, we divide the experimentally derived mass of each element by the overall mass of the compound, and then convert to a percentage:

% C = \dfrac{7.34 \;\text{g C}}{12.04 \;\text{g compound}} × 100% = 61.0%

% H = \dfrac{1.85 \;\text{g H}}{12.04 \;\text{g compound}} × 100% = 15.4%

% N = \dfrac{2.85 \;\text{g N}}{12.04 \;\text{g compound}} × 100% = 23.7%

The analysis results indicate that the compound is 61.0% C, 15.4% H, and 23.7% N by mass.

Check Your Learning
A 24.81-g sample of a gaseous compound containing only carbon, oxygen, and chlorine is determined to contain 3.01 g C, 4.00 g O, and 17.81 g Cl. What is this compound’s percent composition?

Answer:

12.1% C, 16.1% O, 71.8% Cl

Determining Percent Composition from Formula Mass

Percent composition is also useful for evaluating the relative abundance of a given element in different compounds of known formulas. As one example, consider the common nitrogen-containing fertilizers ammonia (NH3), ammonium nitrate (NH4NO3), and urea (CH4N2O). The element nitrogen is the active ingredient for agricultural purposes, so the mass percentage of nitrogen in the compound is a practical and economic concern for consumers choosing among these fertilizers. For these sorts of applications, the percent composition of a compound is easily derived from its formula mass and the atomic masses of its constituent elements. A molecule of NH3 contains one N atom with a mass of 14.01 amu and three H atoms with a total mass of (3 × 1.008 amu) = 3.024 amu. The formula mass of ammonia is therefore (14.01 amu + 3.024 amu) = 17.03 amu, and its percent composition is:

% N = \dfrac{14.01 \;\text{amu N}}{17.03 \;\text{amu NH}_3} × 100% = 82.27%

% H = \dfrac{3.024 \;\text{amu H}}{17.03 \;\text{amu NH}_3} × 100% = 17.76%

This same approach may be taken considering a pair of molecules, a dozen molecules, or a mole of molecules, etc. The latter amount is most convenient and would simply involve the use of molar masses instead of atomic and formula masses, as demonstrated in Example 10. As long as we know the chemical formula of the substance in question, we can easily derive percent composition from the formula mass or molar mass.

Example 10

Determining Percent Composition from a Molecular Formula
Aspirin is a compound with the molecular formula C9H8O4. What is its percent composition?

Solution
To calculate the percent composition, we need to know the masses of C, H, and O in a known mass of C9H8O4. It is convenient to consider 1 mol of C9H8O4 and use its molar mass (180.159 g/mole, determined from the chemical formula) to calculate the percentages of each of its elements:

% C = \dfrac{9 \;\text{mol C} \times \text{molar mass C}}{\text{molar mass} \;\text{C}_9\text{H}_{8}\text{O}_4} × 100% = \dfrac{9 \times 12.01 \;\text{g/mol}} {180.159 \;\text{g/mol}} × 100% = \dfrac{108.09 \;\text{g/mol}}{180.159\;\text{g/mol}} × 100%

% C = 60.00%

% H = \dfrac{8 \;\text{mol H} \times \text{molar mass H}}{\text{molar mass} \;\text{C}_9\text{H}_{8}\text{O}_4} × 100% = \dfrac{8 \times 1.008 \;\text{g/mol}} {180.159 \;\text{g/mol}} × 100% = \dfrac{8.064 \;\text{g/mol}}{180.159\;\text{g/mol}} × 100%

% H = 4.476%

% O = \dfrac{4 \;\text{mol O} \times \text{molar mass O}}{\text{molar mass} \;\text{C}_9\text{H}_{8}\text{O}_4} × 100% = \dfrac{4 \times 16.00 \;\text{g/mol}} {180.159 \;\text{g/mol}} × 100% = \dfrac{64.00 \;\text{g/mol}}{180.159\;\text{g/mol}} × 100%

% O = 35.52%

Note that these percentages sum to equal 100.00% when appropriately rounded.

Check Your Learning
To three significant digits, what is the mass percentage of iron in the compound Fe2O3?

Answer:

% Fe = 69.9%

Key Concepts and Summary

The formula mass of a substance is the sum of the average atomic masses of each atom represented in the chemical formula and is expressed in atomic mass units. The formula mass of a covalent compound is also called the molecular mass. A convenient amount unit for expressing very large numbers of atoms or molecules is the mole. One mole of substance is defined to be 6.022 × 1023, a quantity called Avogadro’s number. The mass in grams of 1 mole of substance is its molar mass. Due to the use of the same reference substance in defining the atomic mass unit and the mole, the formula mass (amu) and molar mass (g/mol) for any substance are numerically equivalent (for example, one H2O molecule has a mass of 18 amu and 1 mole of H2O molecules has a mass of 18 g).

The chemical identity of a substance is defined by the types and relative numbers of atoms composing its fundamental entities (molecules in the case of covalent compounds, ions in the case of ionic compounds). A compound’s percent composition provides the mass percentage of each element in the compound.

Key Equations

  • % X = 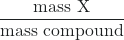\dfrac{\text{mass X}}{\text{mass compound}} × 100%

Glossary

Avogadro’s number (NA)
the number of entities comprising 1 mole of substance, equal to 6.022 × 1023 mol−1
formula mass
sum of the average masses for all atoms represented in a chemical formula; for covalent compounds, this is also the molecular mass
molar mass
mass in grams of 1 mole of a substance
mole
amount of substance containing 6.022 × 1023 atoms, molecules, ions, or other entities

Chemistry End of Section Exercises

Moles, Molar Mass
  1. What is the total mass (amu) of carbon in each of the following molecules?
    1. CH4
    2. C12H10O6
  2. Calculate the molecular or formula mass of each of the following:
    1. P4
    2. Ca(NO3)2
  3. Determine the molecular mass of the following compounds:
    1. A structure is shown. Two C atoms form double bonds with each other. The C atom on the left forms a single bond with two H atoms each. The C atom on the right forms a single bond with an H atom and with a C H subscript 2 C H subscript 3 group.
    2. A structure is shown. A P atom forms a double bond with an O atom. It also forms a single bond with an O atom which forms a single bond with an H atom. It also forms a single bond with another O atom which forms a single bond with an H atom. It also forms a single bond with another O atom which forms a single bond with an H atom.
  4. Which molecule has a molecular mass of 28.05 amu?
    1. A structure is shown. A C atom forms a triple bond with another C atom. Each C atom also forms a single bond with an H atom.
    2. A structure is shown. Two C atoms form a double bond with each other. Each C atom also forms a single bond with two H atoms.
    3. A structure is shown. A C atom forms a single bond with three H atoms each and with another C atom. The second C atom also forms a single bond with three H atoms each.
  5. Write a sentence that describes how to determine the number of moles of a compound in a known mass of the compound if we know its molecular formula.
  6. Compare 1 mole of H2, 1 mole of O2, and 1 mole of F2.
    1. Which has the largest number of molecules? Explain why.
    2. Which has the greatest mass? Explain why.
  7. Which contains the greatest mass of oxygen: 0.75 mol of ethanol (C2H5OH), 0.60 mol of formic acid (HCO2H), or 1.0 mol of water (H2O)? Explain why.
  8. Which contains the greatest number of moles of oxygen atoms: 1 mol of ethanol (C2H5OH), 1 mol of formic acid (HCO2H), or 1 mol of water (H2O)? Explain why.
  9. How are the molecular mass and the molar mass of a compound similar and how are they different?
  10. Calculate the molar mass of each of the following:
    1. C5H12
    2. Sc2(SO4)3
  11. Determine the number of moles of compound and the number of moles of each type of atom in each of the following:
    1. 25.0 g of propylene, C3H6
    2. 3.06 × 10−3 g of the amino acid glycine, C2H5NO2
    3. 25 lb of the herbicide Treflan, C13H16N2O4F (1 lb  =  454 g)
    4. 0.125 kg of the insecticide Paris Green, Cu4(AsO3)2(CH3CO2)2
    5. 325 mg of aspirin, C6H4(CO2H)(CO2CH3)
  12. Determine the mass of each of the following:
    1. 0.0146 mol KOH
    2. 10.2 mol ethane, C2H6
    3. 1.6 × 10−3 mol Na2 SO4
    4. 6.854 × 103 mol glucose, C6 H12 O6
    5. 2.86 mol Co(NH3)6Cl3
  13. Determine the mass in grams of each of the following:
    1. 0.600 mol of oxygen atoms
    2. 0.600 mol of oxygen molecules, O2
    3. 0.600 mol of ozone molecules, O3
  14. Determine the number of atoms and the mass of zirconium, silicon, and oxygen found in 0.3384 mol of zircon, ZrSiO4, a semiprecious stone.
  15. Determine which of the following contains the greatest mass of aluminum: 122 g of AlPO4, 266 g of Al2C16, or 225 g of Al2S3.
  16. The Cullinan diamond was the largest natural diamond ever found (January 25, 1905). It weighed 3104 carats (1 carat  =  200 mg). How many carbon atoms were present in the stone?
  17. One 55-gram serving of a particular cereal supplies 270 mg of sodium, 11% of the recommended daily allowance. How many moles and atoms of sodium are in the recommended daily allowance?
  18. A tube of toothpaste contains 0.76 g of sodium monofluorophosphate (Na2PO3F) in 100 mL.
    1. What mass of fluorine atoms in mg was present?
    2. How many fluorine atoms were present?
  19. Which of the following represents the least number of molecules?
    1. 20.0 g of H2O (18.02 g/mol)
    2. 77.0 g of CH4 (16.06 g/mol)
    3. 68.0 g of CaH2 (42.09 g/mol)
    4. 100.0 g of N2O (44.02 g/mol)
    5. 84.0 g of HF (20.01 g/mol)
  20. Given 1.0 mole of the following substances, which has the greatest number of ions?
    1. KClO4
    2. Li2SO4
    3. NH4CH3COO
    4. LiHCO3
    5. NaNO3
  21. Select the 1.000 g sample with the largest number of molecules.
    1. nitrogen gas
    2. oxygen gas
    3. fluorine gas
    4. chlorine gas
    5. All samples have the same number of particles.
Percent Composition
  1. Calculate the following to 3 significant figures:
    1. the percent composition of nitrogen in ammonia, NH3
    2. the percent composition of oxygen in sodium thiosulfate, Na2S2O3
    3. the percent of calcium in Ca3(PO4)2
  2. Determine the following to four significant figures:
    1. the percent composition of nitrogen in hydrazoic acid, HN3
    2. the percent composition of carbon in TNT, C6H2(CH3)(NO2)3
    3. the percent of aluminum in aluminum sulfate, Al2(SO4)3
  3. You have 1.0 mol of the following compounds.  Select the compound with the smallest percent composition of chlorine.
    1. Barium chloride
    2. Magnesium chloride
    3. Calcium chloride
    4. Nickel(II) chloride

Answers to Chemistry End of Section Exercises

  1. (a) 12.01 amu;  (b) 144.12 amu
  2. (a) 123.896 amu;  (b) 164.086 amu;
  3. (a) 56.107 amu;  (b) 97.9950 amu
  4. B
  5. Use the molecular formula to find the molar mass; to obtain the number of moles, divide the mass of compound by the molar mass of the compound expressed in grams.
  6. (a) They all have the same number of molecules because there is one mole of each, and one mole is always 6.022 × 1023 molecules per mole;
    (b) F2 has the greatest mass because it is greater in mass than hydrogen and oxygen
  7. Formic acid. Its formula has twice as many oxygen atoms as the other two compounds (one each). Therefore, 0.60 mol of formic acid would be equivalent to 1.20 mol of a compound containing a single oxygen atom.
  8. Formic acid because there are two moles of oxygen in one mole of formic acid whereas ethanol and water only have one.
  9. The two masses have the same numerical value, but the units are different: The molecular mass is the mass of 1 molecule while the molar mass is the mass of 6.022 × 1023 molecules.
  10. (a) 72.150 g/mol; (b) 378.103 g/mol
  11. (a) 0.594 mol propylene, 1.78 mol C, 3.56 mol H;
    (b) 4.08 × 10-5 mol glycine, 8.15 × 10-5 mol C, 2.04 × 10-4 mol H, 4.08 × 10-5 mol N, 8.15 × 10-5 mol O;
    (c) 40 mol Treflan, 520 mol C, 640 mol H, 80 mol N, 160 mol O, 40 mol F;
    (d) 0.202 mol Paris Green, 0.808 mol Cu, 0.404 mol As, 2.02 mol O, 0.808 mol C, 1.212 mol H;
    (e) 1.80 × 10-3 mol Aspirine, 1.62 × 10-2 mol C, 1.44 × 10-2 mol H, 7.22 × 10-3 mol O
  12. (a) 0.819 g; (b) 307 g; (c) 0.23 g; (d) 1.235 × 106 g (1235 kg); (e) 765 g
  13. (a) 9.60 g; (b) 19.2 g; (c) 28.8 g
  14. zirconium: 2.038 × 1023 atoms; 30.87 g; silicon: 2.038 × 1023 atoms; 9.504 g; oxygen: 8.151 × 1023 atoms; 21.66 g
  15. AlPO4: 1.00 mol, Al2Cl6: 0.994 mol, Al2S3: 1.50 mol. Thus, Al2S3 contains the greatest mass of aluminum
  16. 3.113 × 1025 C atoms
  17. 0.107 mol Na, 6.43 × 1022 atoms Na
  18. (a) 0.10 g Fluorine; (b) 3.18 × 1021 atoms Fluorine
  19. A
  20. B
  21. A
  22. (a) 82.2%; (b) 30.4%; (c) 38.8%
  23. (a) 97.66%; (b) 37.02%; (c) 15.77%
  24. A
Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 103/104 Resource Book Copyright © by Chem 103 Textbook Team and Chem 104 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.