M6Q5: Calorimetry continued: Types of Calorimeters and Analyzing Heat Flow

Chem 103 Textbook Team; Chem 104 Textbook Team

M6Q5: Calorimetry continued: Types of Calorimeters and Analyzing Heat Flow

Introduction

This section introduces calorimetry, an experimental method used to determine quantitative values of thermodynamic properties of substances. Calorimetry experiments take place in a calorimeter, a device in which the energy released or absorbed by a chemical or physical process can be determined by measuring the heat transferred. This section includes worked examples, sample problems, and a glossary.

Learning Objectives for Calorimetry: Types of Calorimeters and Analyzing Heat Flow

Identify the relationship between heat, mass, temperature change, and heat capacities and solve problems that quantify heat flow.
| Calorimetry | Heat Flow When Hot Metals are Placed in Water | Heat Flow When Chemical Reactions Occur | Coffee Cup Calorimetry |

Calorimetry

One technique we can use to measure the amount of heat involved in a chemical or physical process is known as calorimetry. In a calorimetry experiment, measurements of temperature changes are made inside a calorimeter, a calibrated device with a known heat capacity. The data can then be used to calculate the amount of heat transferred.

The measurement of heat transfer using this approach requires the definition of a system (the substance(s) undergoing the chemical or physical change) and its surroundings (the other components of the measurement apparatus that serve to either provide heat to the system or absorb heat from the system). Knowledge of the heat capacity of the surroundings, and careful measurements of the masses of the system and surroundings and their temperatures before and after the process, allows one to calculate the heat transferred as described in this section.

Heat flow when hot metals are placed in water

Let us first consider a simple example that illustrates the core idea behind calorimetry.

Suppose we initially have a high-temperature substance, such as a hot piece of metal (M), and a low-temperature substance, such as cool water (W). If they are brought into contact, heat will flow from metal to water. The temperature of the metal will decrease, and the temperature of the water will increase, until the two substances have the same temperature—that is, when they reach thermal equilibrium (Figure 1).

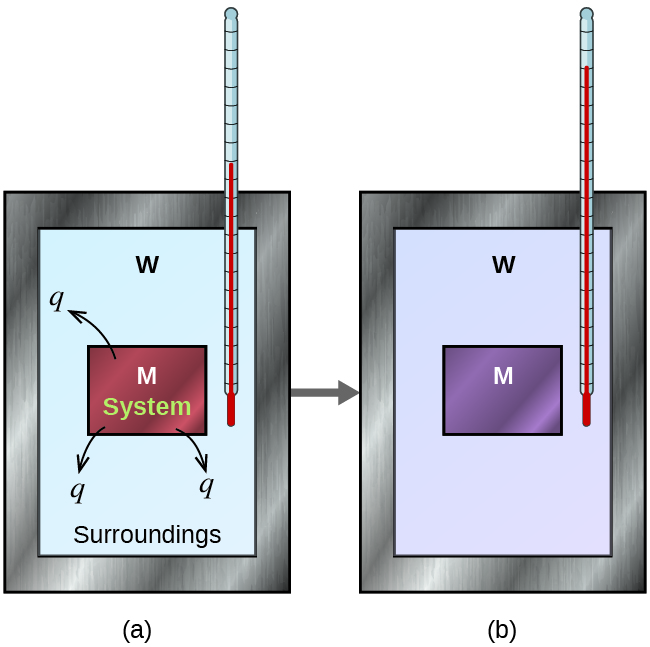
Two diagrams are shown and labeled a and b. Each diagram is composed of a rectangular container with a thermometer inserted inside from the top right corner. Both containers are connected by a right-facing arrow. Both containers are full of water, which is depicted by the letter “W,” and each container has a square in the middle which represents a metal which is labeled with a letter “M.” In diagram a, the metal is drawn in brown and has three arrows facing away from it. Each arrow has the letter “q” at its end. The metal is labeled “system” and the water is labeled “surroundings.” The thermometer in this diagram has a relatively low reading. In diagram b, the metal is depicted in purple and the thermometer has a relatively high reading. — **Figure 1.** In a simple calorimetry process, (a) heat, q, is transferred from the hot metal (M) to the cool water (W) until (b) both are at the same temperature.

If this occurs in an ideal calorimeter, all of the heat transfer would occur between the two substances and no heat is gained or lost by the calorimeter or the environment outside of the calorimeter. In other words, the net heat change is zero:

q_metal + q_water = 0

In this example, we can define the metal as the system and the water as the surrounding. Rearranging the above equation shows that:

q_metal = –q_water

The magnitude of the heat (change) is therefore the same for system and surrounding (the amount of heat gained by the water as it warms is the same as the amount of heat lost by the metal as it cools). The negative sign in front of q_water merely shows that it is opposite in direction of heat flow as q_metal, but does not indicate the arithmetic sign of either q value (that is determined by whether the matter in question gains or loses heat, per definition).

Example 1

Heat Transfer between Substances at Different Temperatures
A 360 g piece of rebar (a steel rod used for reinforcing concrete) is dropped into 425 mL of water at 24.0 °C. The final temperature of the water was measured as 42.7 °C. Calculate the initial temperature of the piece of rebar. Assume the specific heat of steel is approximately the same as that for iron (Specific Heat Table), and that all heat transfer occurs between the rebar and the water (there is no heat exchange with the surroundings).

Solution
The temperature of the water increases from 24.0 °C to 42.7 °C, so the water absorbs heat. That heat came from the piece of rebar, which initially was at a higher temperature. Assuming that all heat transfer was between the rebar and the water, with no heat “lost” elsewhere, then heat given off by rebar = −heat taken in by water, or:

q_rebar = –q_water

Since we know how heat is related to other measurable quantities, we have:

(c × m × ∆T)_rebar = -(c × m × ∆T)_water

Letting f = final and i = initial, in expanded form, this becomes:

c_rebar × m_rebar × (T_{f, rebar} – T_{i, rebar}) = -c_water × m_water × (T_{f, water}– T_{i, water})

The density of water is 1.0 g/mL, so 425 mL of water = 425 g. Noting that the final temperature of both the rebar and water is 42.7 °C, substituting known values yields:

(0.449 J/(g·°C))(360 g)(42.7 °C – T_{i, rebar}) = (4.184 J/(g·°C))(425 g)(42.7 °C – 24.0 °C)

$\text{T}_{\text{i, rebar}} = \dfrac{(4.184\;\text{J/g} {\cdot} {^\circ}\text{C})(425 \;\text{g})(42.7 \;^\circ\text{C} - 24.0 \;^\circ\text{C})}{(0.449 \;\text{J/g} {\cdot} ^\circ\text{C})(360 \;\text{g})} + 42.7 \;^\circ\text{C}$

Solving this gives T_{i, rebar}= 248 °C, so the initial temperature of the rebar was 248 °C.

Check Your Learning
A 248 g piece of copper is dropped into 390 mL of water at 22.6 °C. The final temperature of the water was measured as 39.9 °C. Calculate the initial temperature of the piece of copper. Assume that all heat transfer occurs between the copper and the water.

Answer:

The initial temperature of the copper was 335.6 °C.

This method can also be used to determine other quantities, such as the specific heat of an unknown metal.

Example 2

Identifying a Metal by Measuring Specific Heat
A 59.7 g piece of metal that had been submerged in boiling water was quickly transferred into 60.0 mL of water initially at 22.0 °C. The final temperature is 28.5 °C. Use these data to determine the specific heat of the metal. Use this result to identify the metal.

Solution
Assuming perfect heat transfer, heat given off by metal = −heat taken in by water, or:

q_metal + q_water = 0

In expanded form, this is:

c_metal × m_metal × (T_{f, metal} – T_{i, metal}) = -c_water × m_water × (T_{f, water} – T_{i, water})

Noting that since the metal was submerged in boiling water, its initial temperature was 100.0 °C; and that for water, 60.0 mL = 60.0 g; we have:

(c_metal)(59.7 g)(28.5 °C – 100.0 °C) = -(4.184 J/(g·°C))(60.0 g)(28.5 °C – 22.0 °C)

Solving for c_metal gives:

$\text{c}_{\text{metal}} = \dfrac{-(4.184 \;\text{J/g} {\cdot} ^\circ\text{C})(60.0 \;\text{g})(6.5 \;^\circ\text{C})}{(59.7 \;\text{g})(-71.5 \;^\circ\text{C})} = 0.38\;\text{J/g} {\cdot} ^\circ\text{C}$

Comparing this with values in the Specific Heats Table, our experimental specific heat is closest to the value for copper (0.39 J/(g·°C)), so we identify the metal as copper.

Check Your Learning
A 92.9 g piece of a silver/gray metal is heated to 178.0 °C, and then quickly transferred into 75.0 mL of water initially at 24.0 °C. After 5 minutes, both the metal and the water have reached the same temperature: 29.7 °C. Determine the specific heat and the identity of the metal. (Note: You should find that the specific heat is close to that of two different metals. Explain how you can confidently determine the identity of the metal).

Answer:

c_metal = 0.13 J/(g·°C)

This specific heat is close to that of either gold or lead. It would be difficult to determine which metal this was based solely on the numerical values. However, the observation that the metal is silver/gray in addition to the value for the specific heat indicates that the metal is lead.

Heat flow when chemical reactions occur

When an exothermic reaction occurs in solution in a calorimeter, the heat produced by the reaction is absorbed by the solution, which increases the solution’s temperature. When an endothermic reaction occurs, the heat required is absorbed from the thermal energy of the solution, which decreases the solution’s temperature (Figure 2). This temperature change, along with the specific heat and mass of the solution, can then be used to calculate the amount of heat involved in the chemical reaction.

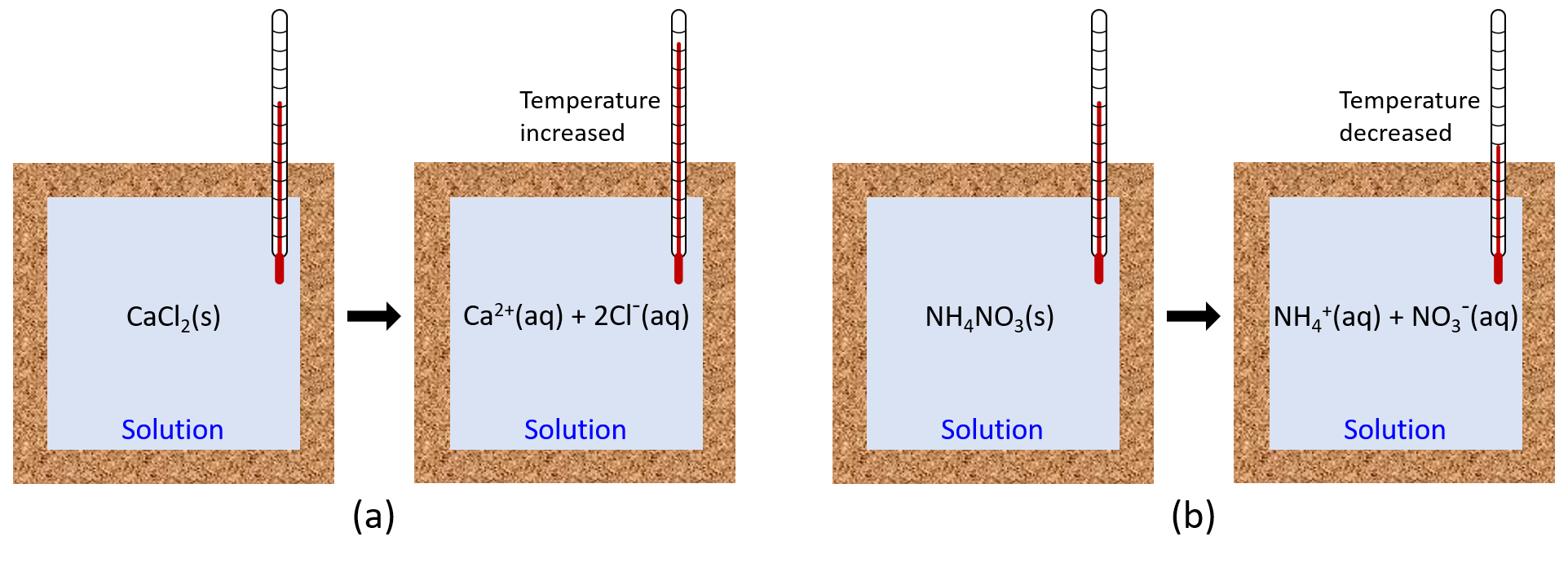
Two diagrams labeled a and b are shown. Each is made up of two rectangular containers with a thermometer inserted into the top right and extending inside. There is a right facing arrow connecting each box in each diagram. The left container in diagram a depicts a solution with the term “CaCl2(s)” written in the center. The label “Solution” are written at the bottom of the container. The right container in diagram a has the term “Ca2+(aq) + 2Cl-(aq)” written in the center and “Solution” written at the bottom of the container. The phrase “Temperature increased” is next to the thermometer. The left container in diagram b depicts a solution with the terms “NH4NO3(s)” written in the center and “Solution” written at the bottom. The right container in diagram b has the term — **Figure 2**. (a) An exothermic reaction occurs and heat is transferred to the solution, raising the solution temperature. (b) An endothermic reaction occurs and heat is transferred from the solution, lowering the solution temperature.

Oftentimes, we do not have a clear boundary between the chemical reaction and the solution in which it occurs (the chemical compounds are typically well-dispersed throughout the solution). Hence, we define the entire reaction solution as the system. If the experiment is conducted within an ideal calorimeter, then heat lost to matter outside the calorimeter (the surroundings) is zero, and:

q_system = 0 = q_reaction + q_solution

This means that the amount of heat produced or consumed by the reaction equals the amount of heat absorbed or lost by the solution:

q_reaction = -q_solution

This equation will be extremely useful with heat-transfer related problems.

Demonstration: Heat of neutralization reaction

Set up. The following demonstration illustrates using calorimetry to measure the heat of the neutralization reaction between HCl and NaOH. First, HCl is added to an insulated container and the temperature probe is placed into the solution. An initial temperature reading is recorded on the computer. The lid is briefly lifted and the NaOH is added. The lid is then quickly replaced and the temperature change is observed.

Prediction. Before watching the video, write the reaction equation for this neutralization reaction.

Explanation. The reaction occurring here is:

HCl(aq) + NaOH(aq) → H₂O(ℓ) + NaCl(aq)

The initial temperature reading of the HCl was stabilized at 22.4 °C. When the NaOH is added, the temperature of the solution increases to 66.3 °C. Since the temperature of the solution increased, we know that the q_solution is positive (positive ΔT) and therefore the q_reaction must be negative. This indicates that the reaction is an exothermic reaction. An exothermic reaction releases energy and thus increases the temperature of the solution.

Note: If you look closely at the temperature reading at the end of the video, you’ll notice that the temperature reaches a maximum of 66.3 °C, but then starts to decrease again and reaches 65.7 °C at the end of the video. This decrease in temperature that happens after the reaction occurs is due to heat escaping from the insulated container. When you perform similar experiments in the lab, you will want to note the highest (or lowest) temperature reached for the reaction since imperfect insulation of the container causes the temperature to drop (or increase) after the reaction is completed and is not a result of the thermochemistry of the reaction being studied.

Example 3

Heat Produced by an Exothermic Reaction
When 50.0 mL of 0.10 M HCl(aq) and 50.0 mL of 0.10 M NaOH(aq), both at 22.0 °C, are added to a calorimeter, the temperature of the mixture reaches a maximum of 28.9 °C. What is the approximate amount of heat produced by this reaction?

HCl(aq) + NaOH(aq) → NaCl(aq) + H₂O(ℓ)

Solution
To visualize what is going on, imagine that you could combine the two solutions so quickly that no reaction took place while they mixed; then after mixing, the reaction took place. At the instant of mixing, you have 100.0 mL of a mixture of HCl and NaOH at 22.0 °C. The HCl and NaOH then react until the solution temperature reaches 28.9 °C.

The heat given off by the reaction is equal to that absorbed by the solution. Therefore:

q_reaction = –q_solution

(It is important to remember that this relationship only holds if the calorimeter does not absorb any heat from the reaction, and there is no heat exchange the surroundings outside of the calorimeter.)

Next, we know that the heat absorbed by the solution depends on its specific heat, mass, and temperature change:

q_solution = (c × m × ΔT)_solution

To proceed with this calculation, we need to make a few more reasonable assumptions or approximations. Since the solution is aqueous, we can proceed as if it were water in terms of its specific heat and mass values. The density of water is approximately 1.0 g/mL, so 100.0 mL has a mass of about 1.0 × 10² g (two significant figures). The specific heat of water is approximately 4.18 J/g °C, so we use that for the specific heat of the solution. Substituting these values gives:

q_solution = (4.184 J/(g·°C))(1.0 × 10² g)(28.9 °C – 22.0 °C) = 2.89 × 10³ J

Finally, since we are trying to find the heat of the reaction, we have:

q_reaction = –q_solution = -2.89 × 10³ J

The negative sign indicates that the reaction is exothermic. It produces 2.89 kJ of heat.

Check Your Learning
When 100 mL of 0.200 M NaCl(aq) and 100 mL of 0.200 M AgNO₃(aq), both at 21.9 °C, are mixed in a calorimeter, the temperature increases to 23.5 °C as solid AgCl forms. How much heat is produced by this precipitation reaction? What assumptions did you make to determine your value?

Answer:

1.34 × 10³ J; assume no heat is absorbed by the calorimeter, no heat is lost to the surroundings outside of the calorimeter, and that the specific heat and mass of the solution are the same as those for water.

Chemistry in Real Life: Thermochemistry of Hand Warmers

When working or playing outdoors on a cold day, you might use a hand warmer to warm your hands (Figure 3). A common reusable hand warmer contains a supersaturated solution of NaC₂H₃O₂ (sodium acetate) and a metal disc. Bending the disk creates nucleation sites around which the NaC₂H₃O₂ quickly crystallizes (a later chapter on solutions will investigate saturation and supersaturation in more detail).

The process

NaC₂H₃O₂(aq) → NaC₂H₃O₂(s)

is exothermic, and the heat produced by this process is absorbed by your hands, thereby warming them (at least for a while). If the hand warmer is reheated, the NaC₂H₃O₂ redissolves and can be reused.

A series of three photos is shown. There are two right-facing arrows connecting one photo to the next. The first photo shows a chemical hand warmer. It is a bag that contains a clear, colorless liquid. There is a white disk located to the right inside the bag. The second photo shows the same thing, except the white disc has become a white, cloudy substance. The third photo shows the entire bag filled with this white substance. — **Figure 3.** Chemical hand warmers produce heat that warms your hand on a cold day. In this one, you can see the metal disc that initiates the exothermic precipitation reaction. (credit: modification of work by Science Buddies TV/YouTube)

Another common hand warmer produces heat when it is ripped open, exposing iron and water in the hand warmer to oxygen in the air. One simplified version of this exothermic reaction is

2Fe(s) + $\frac{3}{2}$ O₂(g) → Fe₂O₃(s)

Salt in the hand warmer catalyzes the reaction, so it produces heat more rapidly; cellulose, vermiculite, and activated carbon help distribute the heat evenly. Other types of hand warmers use lighter fluid (a platinum catalyst helps lighter fluid oxidize exothermically), charcoal (charcoal oxidizes in a special case), or electrical units that produce heat by passing an electrical current from a battery through resistive wires.

This link shows the precipitation reaction that occurs when the disk in a chemical hand warmer is flexed.

Example 4

Heat Flow in an Instant Ice Pack
When solid ammonium nitrate dissolves in water, the solution becomes cold. This is the basis for an “instant ice pack” (Figure 4). When 3.21 g of solid NH₄NO₃ dissolves in 50.0 g of water at 24.9 °C in a calorimeter, the temperature of the solution decreases to 20.3 °C.

Calculate the value of q for this reaction and explain the meaning of its arithmetic sign. State any assumptions that you made.

A diagram depicts a rectangular pack containing a white, solid substance and an interior bag full of water. The white solid is labeled “ammonium nitrate.” The top of the packet has the words “Instant Cold Pack” written on it. It also has three pictograms, which from right to left, show a hand squeezing the pack, agitating the pack and placing the pack on a person’s body. The bottom of the pack has printed words that read “single use only.” — **Figure 4.** An instant cold pack consists of a bag containing solid ammonium nitrate and a second bag of water. When the bag of water is broken, the pack becomes cold because the dissolution of ammonium nitrate is an endothermic process. The cold pack then removes thermal energy from your body.

Solution
We assume that the calorimeter prevents heat transfer between the solution and its external environment (including the calorimeter itself), in which case:

q_reaction = –q_solution

Assuming also that the specific heat of the solution is the same as that for water, we have:

q_reaction = –q_solution = -(c × m × ΔT)_solution
q_reaction = -[(4.184 J/(g·°C)) × (53.2 g) × (20.3 °C – 24.9 °C)]
= -[(4.184 J/(g·°C)) × (53.2 g) × (-4.6 °C)]
= +1.0 × 10³ J = +1.0 kJ

The positive sign for q_reaction indicates that the dissolution is an endothermic process.

Check Your Learning
When a 3.00-g sample of KCl was added to 3.00 × 10² g of water in a calorimeter, the temperature decreased by 1.05 °C. How much heat is involved in the dissolution of the KCl? What assumptions did you make?

Answer:

1.33 kJ; assume that the calorimeter prevents heat transfer between the solution and its external environment (including the calorimeter itself) and that the specific heat of the solution is the same as that for water.

Coffee Cup Calorimetry

Scientists use well-insulated calorimeters to minimize the transfer of heat to the environment outside of the calorimeter. This enables the accurate determination of the heat involved in chemical processes, the energy content of foods, and so on.

Relatively inexpensive calorimeters often consist of two thin-walled cups that are nested in a way that minimizes thermal loss during use, along with an insulated cover, handheld stirrer, and simple thermometer (Figure 5). Many general chemistry labs utilize such coffee cup calorimeters because they are inexpensive and easy to use. The amount of heat absorbed by the calorimeter is often small enough that we can neglect it.

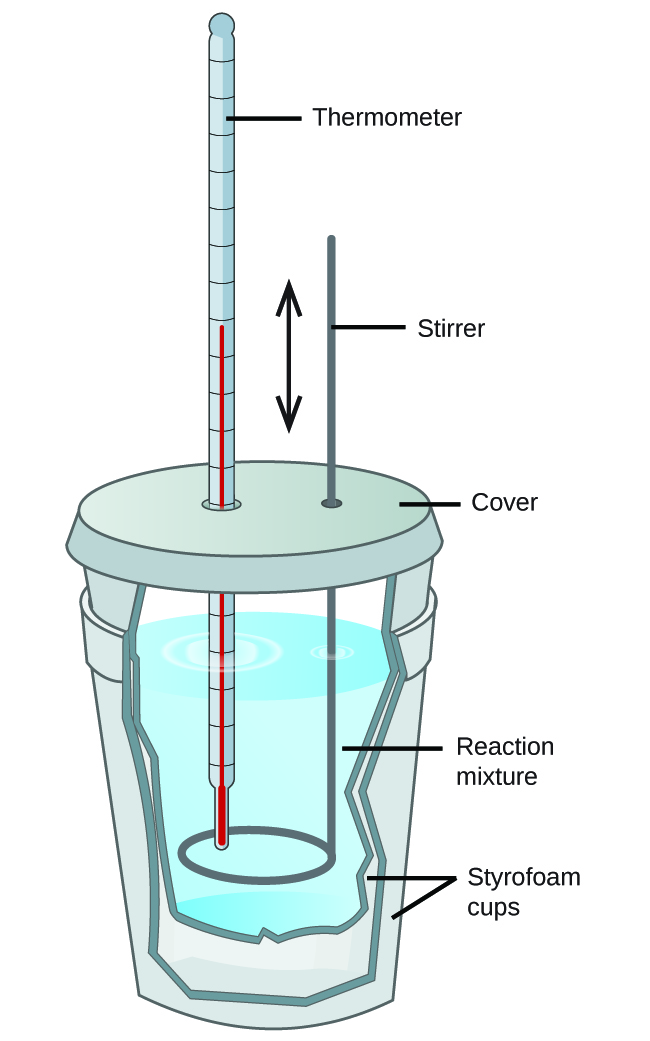
Two Styrofoam cups are shown nested in one another with a cover over the top. A thermometer and stirring rod are inserted through the cover and into the solution inside the cup, which is shown as a cut-away. The stirring rod has a double headed arrow next to it facing up and down. The liquid mixture inside the cup is labeled “Reaction mixture.” — **Figure 5.** A simple calorimeter can be constructed from two polystyrene cups. A thermometer and stirrer extend through the cover into the reaction mixture.

These types of calorimeters operate at constant pressure as the lid is not an air-tight seal and the system is effectively still open to the atmosphere. Since the heat flow that is measured in this case is the heat flow at constant pressure, q_p, this type of calorimeter provides a direct way to find the enthalpy change of the process, ΔH, since ΔH = q_p.

Commercial solution calorimeters are more expensive. Calorimeters used for industry and research typically have a well-insulated, fully enclosed reaction vessel, motorized stirring mechanism, and a more accurate temperature sensor.

Key Concepts and Summary

Calorimeters are designed to minimize energy exchange to the environment outside the calorimeter, yielding more accurate results. The main goal of calorimetry is to determine the heat flow. If an endothermic reaction occurs in a coffee cup calorimeter, the temperature of the solution would decrease because thermal energy from the solution is absorbed by the reaction. If an exothermic reaction occurs in a coffee cup calorimeter, the temperature of the solution would increase as it absorbs the released thermal energy. Heat stops flowing when thermal equilibrium is reached and everything within the calorimeter is the same temperature.

Key Equations

q_reaction + q_solution = 0

Glossary

calorimeter: device used to measure the amount of heat absorbed or released in a chemical or physical process

calorimetry: process of measuring the amount of heat involved in a chemical or physical process

Chemistry End of Section Exercises

How many milliliters of water at 23 °C with a density of 1.00 g/mL must be mixed with 180 mL (about 6 oz) of coffee at 95 °C so that the resulting combination will have a temperature of 60 °C? Assume that coffee and water have the same density and the same specific heat.
A 45-g aluminum spoon (specific heat 0.88 J/g·°C) at 24 °C is placed in 180 mL (180 g) of coffee at 85 °C and the temperature of the two become equal.
1. What is the final temperature when the two become equal? Assume that coffee has the same specific heat as water.
2. The first time a student solved this problem she got an answer of 88 °C. Explain why this is clearly an incorrect answer.
The temperature of the cooling water as it leaves the hot engine of an automobile is 115.6 °C. After it passes through the radiator it has a temperature of 79.4 °C. Calculate the amount of heat transferred (in kJ) from the engine to the surroundings by one gallon of water with a density of 1.00 g/mL and a specific heat of 4.184 J/g·°C.
A 70.0-g piece of metal at 80.0 °C is placed in 100 g of water at 22.0 °C contained in a calorimeter like that shown in Figure 5. The metal and water come to the same temperature at 24.6 °C. How much heat did the metal give up to the water? What is the specific heat of the metal?
If a reaction produces 1.506 kJ of heat, which is trapped in 30.0 g of water initially at 26.5 °C in a calorimeter like that in Figure 5, what is the resulting temperature of the water (in °C)?
Dissolving 3.0 g of CaCl₂(s) in 150.0 g of water in a calorimeter (Figure 5) at 22.4 °C causes the temperature to rise to 25.8 °C. What is the approximate amount of heat (in kJ) involved in the dissolution, assuming the heat capacity of the resulting solution is 4.18 J/g·°C? Is the reaction exothermic or endothermic?
When 50.0 g of 0.200 M NaCl(aq) at 24.1 °C is added to 100.0 g of 0.100 M AgNO₃(aq) at 24.1 °C in a calorimeter, the temperature increases to 25.2 °C as AgCl(s) forms. Assuming the specific heat of the solution and products is 4.20 J/g·°C, calculate the approximate amount of heat in joules produced.
The addition of 3.15 g of Ba(OH)₂·8H₂O to a solution of 1.52 g of NH₄SCN in 100 g of water in a calorimeter caused the temperature to fall by 3.1 °C. Assuming the specific heat of the solution and products is 4.20 J/g·°C, calculate the approximate amount of heat (in kJ) absorbed by the reaction, which can be represented by the following equation:
Ba(OH)₂·8H₂O(s) + 2NH₄SCN(aq) ⟶ Ba(SCN)₂(aq) + 2NH₃(aq) + 10H₂O(ℓ)
The reaction of 50 mL of acid and 50 mL of base described in Example 3 increased the temperature of the solution by 6.9 degrees. How much would the temperature have increased if 100 mL of acid and 100 mL of base had been used in the same calorimeter starting at the same temperature of 22.0 °C? Explain your answer.
If the 3.21 g of NH₄NO₃ in Example 4 were dissolved in 100.0 g of water under the same conditions, how much would the temperature change? Explain your answer.
In a coffee-cup calorimeter, you add 100.0 mL of 0.400 M HCl solution to excess solid magnesium. The initial temperature of the solution was 25.0 °C. Assume the mass of the solution plus metal is 100.0 g (with density 1.00 g/mL), and the heat capacity of the final solution is 4.184 J/(g °C).
Mg(s) + 2 HCl(aq) → MgCl₂(aq) + H₂(g) Δ_rH° = –466.8 kJ/mol
1. Calculate the heat gained or lost by the solution during this reaction in kJ.
2. Determine the final temperature of the solution.
3. You repeat the experiment, and this time you react excess Mg(s) with 150.0 mL of 0.400 M HCl. Assume the mass of the solution plus metal is 150.0 g. Fill in the following blanks, the choices are: “Greater than”, “Less than”, or “The same as”
  1. The heat released when excess Mg(s) reacts with the 150.0 mL of 0.400 M HCl is _____ the heat when 100.0 mL was used.
  2. The magnitude of the temperature change of the solution when excess Mg(s) reacts with the 150.0 mL of 0.400 M HCl is _____ the magnitude of the temperature change when 100.0 mL was used.
  3. The enthalpy change (in kJ/mol) when excess Mg(s) reacts with the 150.0 mL of 0.400 M HCl is _____ the enthalpy change when 100.0 mL was used.
The balanced equation for the reaction between sulfuric acid and sodium hydroxide is:
H₂SO₄(aq) + 2 NaOH(aq) → Na₂SO₄(aq) + 2 H₂O(ℓ)

62.5 mL of 0.910 M NaOH and 50.0 mL of 0.684 M H2SO4, both at 22.0 °C, were added to a coffee cup calorimeter. The maximum temperature reached was 28.9 °C. What is the enthalpy of reaction, Δ_rH°, for the balanced chemical reaction shown above? (Assume no heat is lost to the calorimeter, the density of the solution is 1.00 g/mL, and the specific heat of the solution is 4.18 J/g·°C.)
The amount of fat recommended for someone with a daily diet of 2000 Calories is 65 g. What percent of the calories in this diet would be supplied by this amount of fat if the average number of Calories for fat is 9.1 Calories/g?
A teaspoon of the carbohydrate sucrose (common sugar) contains 16 Calories (16 kcal). What is the mass of one teaspoon of sucrose if the average number of Calories for carbohydrates is 4.1 Calories/g?
What is the maximum mass of carbohydrate (in grams) in a 6-oz serving of diet soda that contains less than 1 Calorie per can if the average number of Calories for carbohydrates is 4.1 Calories/g?
A pint of premium ice cream can contain 1100 Calories. What mass of fat, in grams and pounds, must be produced in the body to store an extra 1.1 × 10³ Calories if the average number of Calories for fat is 9.1 Calories/g?
A serving of a breakfast cereal contains 3 g of protein, 18 g of carbohydrates, and 6 g of fat. What is the Calorie content of a serving of this cereal if the average number of Calories for fat is 9.1 Calories/g, for carbohydrates is 4.1 Calories/g, and for protein is 4.1 Calories/g?

Answers to Chemistry End of Section Exercises

170 mL
(a) 82 °C
(b) Because 88°C is higher than the starting temperatures of the coffee and the spoon, which is impossible.
573 kJ
1088 J; the specific heat of the metal is 0.28 J/g °C
38.5 °C
2.2 kJ; The heat produced shows that the reaction is exothermic.
693 J
1.4 kJ
6.9 °C; The total heat released would double because the volume (mass) doubled, ΔT would still be 6.9 °C.
+2.3 °C. Since the mass and the heat capacity of the solution is approximately equal to that of the water, the two-fold increase in the amount of water leads to a two-fold decrease of the temperature change.
(a) q_solution = +9.34 kJ
(b) 47.3 °C
(c) (i) greater than; (ii) the same as; (iii) the same as
Δ_rH° = –114 kJ/mol
30%
3.9 g
0.24 g
1.2 × 10² g; 0.26 pounds
1.4 × 10² Calories

Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 103/104 Resource Book Copyright © by Chem 103 Textbook Team and Chem 104 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.