M16Q3: How A Buffer Works
Learning Objectives
- Determine the pH of a buffer solution before and after adding a given amount of strong acid or strong base.
- Calculate the changes in concentrations of conjugate acids and bases after addition of a strong acid or base.
| Key Concepts and Summary | Glossary | End of Section Exercises |
Buffer Capacity
Buffer solutions do not have an unlimited capacity to keep the pH relatively constant (Figure 1). If we add so much base to a buffer that the weak acid is exhausted, no more buffering action toward the base is possible. On the other hand, if we add an excess of acid, the weak base would be exhausted, and no more buffering action toward any additional acid would be possible. In fact, we do not even need to exhaust all of the acid or base in a buffer to overwhelm it; its buffering action will diminish rapidly when the concentration of either one of the weak acid/base components falls below 10% of the other.

The buffer capacity is the amount of acid or base that can be added to a given volume of a buffer solution before the pH changes significantly, usually by one unit. Buffer capacity depends on the amounts of the weak acid and its conjugate base that are in a buffer mixture, but using the Henderson-Hasselbalch equation, we can see that if the pH changes by + or – one unit, the ratio of ![]() must be:
must be:
0.1 ≤ ![]() ≤ 10
≤ 10
For example, 1 L of a solution that is 1.0 M in acetic acid and 1.0 M in sodium acetate has a greater buffer capacity than 1 L of a solution that is 0.10 M in acetic acid and 0.10 M in sodium acetate even though both solutions have the same pH. The first solution has more buffer capacity because it contains more acetic acid and acetate ion.
In the following examples, we will walk through calculating the pH of buffer solutions after either a strong acid or base have been added. To do this, we will use SCF tables, which stands for “Start”, “Change”, and “Finish”. We will use these tables much like ICE tables from the Equilibrium section, except that SCF tables only use moles and are used when you are adding a strong acid and/or strong base.
Example 1
pH Changes in Buffered and Unbuffered Solutions
Acetate buffers are used in biochemical studies of enzymes and other chemical components of cells to prevent pH changes that might change the biochemical activity of these compounds.
- Calculate the pH of an acetate buffer that is a mixture with 0.10 M acetic acid and 0.10 M sodium acetate. (Ka = 1.8 x 10-5)
- Calculate the pH after 1.0 mL of 0.10 M NaOH is added to 100 mL of this buffer, giving a solution with a volume of 101 mL.
- For comparison, calculate the pH after 1.0 mL of 0.10 M NaOH is added to 100 mL of an unbuffered solution with a pH of 4.74 (a 1.8 × 10−5 M solution of HCl). The volume of the final solution is 101 mL.
Solution part (a)
To determine the pH of the buffer solution we use the Henderson-Hasselbalch Equation.
pH = pKa + log ![]() = -log(1.8 × 10-5) + log
= -log(1.8 × 10-5) + log ![]() = 4.74
= 4.74
Solution part (b)
(1) we write out the reaction involving the strong base (which can be written as OH–) with the acid of the buffer:
OH–(aq) + CH3COOH(aq) → CH3COO–(aq) + H2O(ℓ)
(2) we create an SCF (Start→Change→Finish) table, finding the moles of everything in our solution to begin with:
1.0 mL × ![]() = 0.00010 moles OH–
= 0.00010 moles OH–
100 mL × ![]() = 0.010 moles CH3COOH
= 0.010 moles CH3COOH
100 mL × ![]() = 0.010 moles CH3COO–
= 0.010 moles CH3COO–
| OH–(aq) + CH3COOH(aq) → CH3COO–(aq) + H2O(ℓ) | ||||
| S (Start) | 0.00010 | 0.010 | 0.010 | – |
| C (Change) | – | |||
| F (Finish) | – | |||
(3) we subtract whichever number of moles is smaller between the two reactants, ensuring that one reactant’s quantity goes to zero and other reactant’s remaining quantity is positive.
| OH–(aq) + CH3COOH(aq) → CH3COO–(aq) + H2O(ℓ) | ||||
| S (Start) | 0.00010 | 0.010 | 0.010 | – |
| C (Change) | -0.00010 | -0.00010 | +0.00010 | – |
| F (Finish) | 0 | 0.0099 | 0.0101 | – |
(4) we ask ourselves “What’s in my beaker?”. In this case, we have excess acetic acid and conjugate base (a buffer!) and we can use the Henderson-Hasselbalch Equation to calculate the pH. Since both species are in the same solution, we do not need to convert moles to concentration before using the Henderson-Hasselbalch Equation.
pH = pKa + log ![]() = -log(1.8 × 10-5) + log
= -log(1.8 × 10-5) + log ![]() = 4.75
= 4.75
Notice that the addition of the NaOH barely changed the pH from the pure buffer!
Solution part (c)
(1) we write out our reaction involving the strong base with HCl:
OH–(aq) + H3O+(aq) → 2 H2O(ℓ)
(2) we create an SCF (Start→Change→Finish) table, finding the moles of everything in our solution to begin with:
1.0 mL × ![]() = 0.00010 moles OH–
= 0.00010 moles OH–
100 mL × ![]() = 1.8 × 10-6 moles H3O+
= 1.8 × 10-6 moles H3O+
| OH–(aq) + H3O+(aq) → 2 H2O(ℓ) | |||
| S (Start) | 0.00010 | 1.8 × 10-6 | – |
| C (Change) | |||
| F (Finish) | |||
(3) we subtract whichever number of moles is smaller between the two reactants, ensuring that one reactant’s quantity goes to zero and other reactant’s remaining quantity is positive.
| OH–(aq) + H3O+(aq) → 2 H2O(ℓ) | |||
| S (Start) | 0.00010 | 1.8 × 10-6 | – |
| C (Change) | -1.8 × 10-6 | -1.8 × 10-6 | |
| F (Finish) | 0.0000982 | 0 | |
(4) we ask ourselves “What’s in my beaker?”. In this case, we have excess strong base and need to calculate the new concentration of the hydroxide ion in order to calculate the resulting pH.
[OH–] = ![]() = 0.000972 M OH–
= 0.000972 M OH–
pOH = -log(0.000972 M OH–) = 3.012
pH = 14.00 – pOH = 10.99
Notice how the same amount of sodium hydroxide caused the pH to shift from 4.74 to 10.99 in an unbuffered solution, whereas it only shifted from 4.74 to 4.75 in a buffer!
Check Your Learning
Show that adding 1.0 mL of 0.10 M HCl changes the pH of 100 mL of a 1.8 × 10−5 M HCl solution from 4.74 to 3.00.
Answer:
Initial pH of 1.8 × 10−5 M HCl solution: pH = -log[H3O+] = -log(1.8 × 10−5) = 4.74
Moles of H3O+ in 100 mL 1.8 × 10−5 M HCl:
(0.100 L) × (1.8 × 10−5 moles/L) = 1.8 × 10−6 moles H3O+
Moles of H3O+ added by the addition of 1.0 mL of 0.10 M HCl:
(0.10 moles/L) × (0.0010 L) = 1.0 × 10−4 moles H3O+ added
Final pH after addition of 1.0 mL of 0.10 M HCl:
pH = -log[H3O+]
= -log![]() = -log
= -log 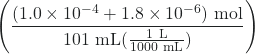 = 3.00
= 3.00
If we add an acid or a base to a buffer that is a mixture of a weak base and its conjugate acid, the calculations of the changes in pH are analogous to those for a buffer mixture of a weak acid and its salt.
Chemistry in Real Life: The Buffer System in Blood
The normal pH of human blood is about 7.4. The carbonate buffer system in the blood uses the following equilibrium reaction:
CO2(g) + 2 H2O(ℓ) ⇌ H2CO3(aq) ⇌ HCO3–(aq) + H3O+(aq)
The concentration of carbonic acid, H2CO3 is approximately 0.0012 M, and the concentration of the hydrogen carbonate ion, HCO3–, is around 0.024 M. Using the Henderson-Hasselbalch equation and the pKa of carbonic acid at body temperature, we can calculate the pH of blood:
pH = pKa + log ![]() = 6.4 + log
= 6.4 + log ![]() = 7.7
= 7.7
The fact that the H2CO3 concentration is significantly lower than that of the HCO3– ion may seem unusual, but this imbalance is due to the fact that most of the by-products of our metabolism that enter our bloodstream are acidic. Therefore, there must be a larger proportion of base than acid, so that the capacity of the buffer will not be exceeded.
Lactic acid is produced in our muscles when we exercise. As the lactic acid enters the bloodstream, it is neutralized by the HCO3– ion, producing H2CO3. An enzyme then accelerates the breakdown of the excess carbonic acid to carbon dioxide and water, which can be eliminated by breathing. In fact, the regulation of CO2 from breathing is a crucial step in the body’s system to regulate pH via carbonate buffer equilibria. If the pH of the blood decreases too far, an increase in breathing removes CO2 from the blood through the lungs driving the equilibrium reaction such that [H3O+] is lowered. If the blood is too basic, a lower breath rate increases CO2 concentration in the blood, driving the equilibrium reaction the other way, increasing [H+] and restoring an appropriate pH.
Key Concepts and Summary
A buffer solution has the capacity to resist a pH change of one unit, or when the ratio of ![]() is: 0.1 ≤
is: 0.1 ≤ ![]() ≤ 10. When calculating the effect a strong acid or base has on the pH of a buffer system, it is important to remember to use an “SCF” or mole table, rather than the ICE tables we have used up to this point. When a strong acid or base are reacting, this reaction is extremely product-favored and we assume the reaction goes to completion. At least one of the reactants must be the limiting reactant and react completely away, leaving a “0” at “F” in the SCF table. If one of the buffer molecules is the limiting reactant and there is excess strong acid or base present, do not forget to divide the moles of strong acid or base by the total volume in order to calculate the remaining concentration of strong acid or base prior to calculating the pH or pOH. This is a detail commonly missed by students in this unit!
≤ 10. When calculating the effect a strong acid or base has on the pH of a buffer system, it is important to remember to use an “SCF” or mole table, rather than the ICE tables we have used up to this point. When a strong acid or base are reacting, this reaction is extremely product-favored and we assume the reaction goes to completion. At least one of the reactants must be the limiting reactant and react completely away, leaving a “0” at “F” in the SCF table. If one of the buffer molecules is the limiting reactant and there is excess strong acid or base present, do not forget to divide the moles of strong acid or base by the total volume in order to calculate the remaining concentration of strong acid or base prior to calculating the pH or pOH. This is a detail commonly missed by students in this unit!
Glossary
- buffer capacity
- amount of acid or base that can be added to a given volume of a buffer solution before the pH changes significantly, usually by one unit.
Chemistry End of Section Exercises
- For a buffer system that consists of 0.25 M benzoic acid, pKa = 4.20, and 0.10 M sodium benzoate, which of the following statements is correct?
- The pH of the buffer = 4.20
- The pH of the buffer is greater than 4.20
- If HCl(aq) is added, the amount of benzoic acid would decrease.
- If NaOH is added, the amount of benzoate would increase.
- If HCl(aq) is added, the pH would increase by a small amount.
- A buffer is created by adding 10.0 mL of 0.250 M HNO3 to 40.0 mL of a 0.500 M NH3 solution. (Kb of NH3 = 1.77 × 10-5)
- What is the pH of the newly created buffer?
- Another 10.0 mL of HNO3 is added to the established buffer, what is the new pH?
- Was the buffer capacity breached upon the second addition (part b) of HNO3?
- 25.0 mL 0.500 M HCl has been added to 100.0 mL of a buffer that is 0.250 M CH3COOH and 0.30 M CH3COO–. What is the original pH of the buffer and how does it change after the HCl addition? (Ka of CH3COOH = 1.8 × 10-5)
- A solution is prepared by dissolving 2.68 grams of ammonium chloride, NH4Cl, (MW: 53.5 g/mol) in 1.0 L of 0.075 M ammonia, NH3. Assume there is no change in the volume of the solution when the ammonium chloride is added. The base ionization constant, Kb, for ammonia is 1.8 × 10-5.
- What is the pH of this solution?
- Suppose that 0.0050 mol of HCl gas is bubbled into the solution described above. What is the pH of the mixture after this addition? Assume there is no change in volume of the solution when the HCl is added.
- Suppose one were to try to filter air filled with toxic levels of nitrogen oxides through a hypoiodite ion, IO–, solution. If these nitrogen oxides create nitric acid when mixed with water, they will react with the hypoiodite ions in solution. Ka(HOI) = 2.3 × 10-11.
- Write the net ionic equation for the reaction that occurs between aqueous sodium hypoiodite, NaIO, and nitric acid, HNO3.
- What is the pH of the bizarre air filter solution after 0.0400 moles of HNO3 have reacted with 50.0 mL of 1.40 M NaIO of the filter?
- When the concentration of the acid and conjugate base of a buffer are present in exactly equimolar proportions, which of the following statements can be concluded? Select all that apply.
- The pH of the buffer solution is equal to the pKa of the acid component of the buffer.
- The buffer is very limited in capacity to absorb either acid or base.
- The buffer has a useful range of pH = 7.00 ± 1.00.
Answers to Chemistry End of Section Exercises
- D
- (a) 10.09
(b) 9.73
(c) No, pH remains within 1 unit of the pKa and 1 ≤![Rendered by QuickLaTeX.com \frac{[\text{base}]}{[\text{acid}]}](https://wisc.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-558a96a657bdca65a67370d2057648e9_l3.png) ≤ 10 remains true
≤ 10 remains true - Buffer pH: 4.82; After HCl addition: 4.41
- (a) 9.43; (b) 9.36
- (a) IO–(aq) + H3O+(aq) → HOI(aq) + H2O(ℓ); (b) 10.52
- A
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

