M11Q5: Types of Unit Cells: Body-Centered Cubic and Face-Centered Cubic

Introduction

In the previous section, we identified that unit cells were the simplest repeating unit of a crystalline solid and examined the most basic unit cell, the primitive cubic unit cell. In this section, we continue by looking at two other unit cell types, the body-centered cubic and the face-centered cubic unit cells.

Learning Objectives for Types of Unit Cells: Body-Centered Cubic and Face-Centered Cubic Cells

|Key Concepts and Summary | Glossary | End of Section Exercises |

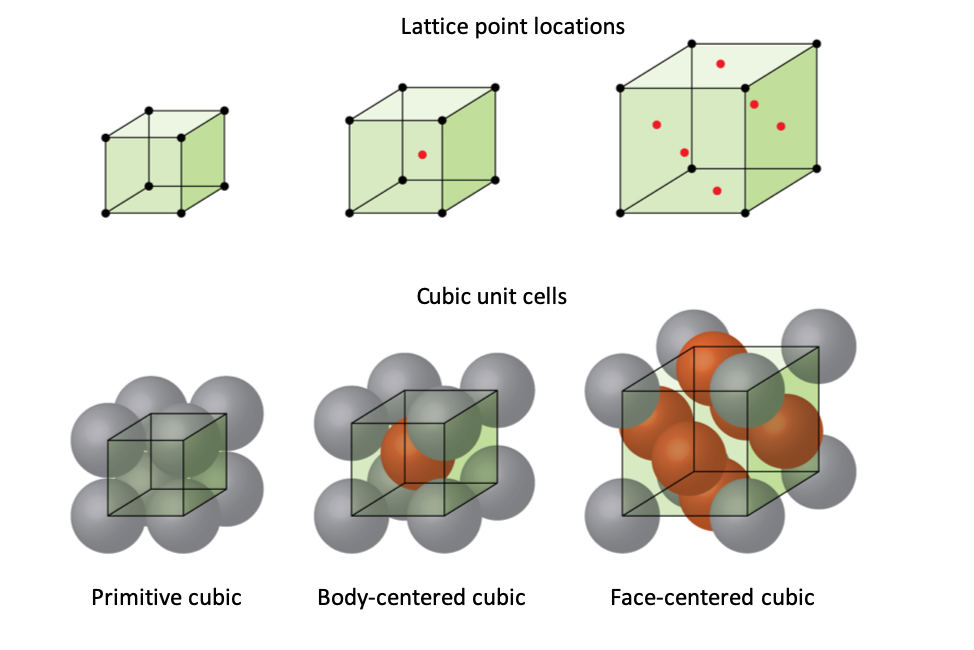
We will focus on the three basic cubic unit cells: primitive cubic (from the previous section), body-centered cubic unit cell, and face-centered cubic unit cell—all of which are illustrated in Figure 1.

Three pairs of images are shown. The first three images are in a row and are labeled “Lattice point locations” while the second three images are in a row labeled “Cubic unit cells.” The first image in the top row shows a cube with black dots at each corner while the first image in the second row is composed of eight spheres that are stacked together to form a cube and dots at the center of each sphere are connected to form a cube shape. The name under this image reads “Simple cubic.” The second image in the top row shows a cube with black dots at each corner and a red dot in the center while the second image in the second row is composed of eight spheres that are stacked together to form a cube with one sphere in the center of the cube and dots at the center of each corner sphere connected to form a cube shape. The name under this image reads “Body-centered cubic.” The third image in the top row shows a cube with black dots at each corner and red dots in the center of each face while the third image in the second row is composed of eight spheres that are stacked together to form a cube with six more spheres located in the center of each face of the cube. Dots at the center of each corner sphere are connected to form a cube shape. The name under this image reads “Face-centered cubic.”
Figure 1. Cubic unit cells of metals show (in the upper figures) the locations of lattice points and (in the lower figures) metal atoms located in the unit cell.

Body-Centered Cubic Cells

Some metals crystallize in an arrangement that has a cubic unit cell with atoms at all of the corners and an atom in the center, as shown in Figure 2. This is called a body-centered cubic (BCC) solid. Atoms in the corners of a BCC unit cell do not contact each other but contact the atom in the center. A BCC unit cell contains two atoms: one-eighth of an atom at each of the eight corners (8 ×  \frac{1}{8} = 1 atom from the corners) plus one atom from the center. Any atom in this structure touches four atoms in the layer above it and four atoms in the layer below it. Thus, an atom in a BCC structure has a coordination number of eight.

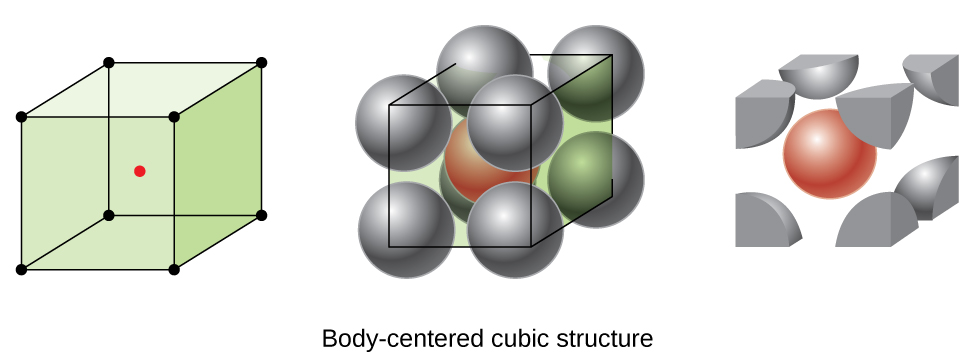
Three images are shown. The first image shows a cube with black dots at each corner and a red dot in the center while the second image is composed of eight spheres that are stacked together to form a cube with one sphere in the center of the cube and dots at the center of each corner sphere connected to form a cube shape. The name under this image reads “Body-centered cubic structure.” The third image is the same as the second, but only shows the portions of the spheres that lie inside the cube shape.
Figure 2. In a body-centered cubic structure, atoms in a specific layer do not touch each other. Each atom touches four atoms in the layer above it and four atoms in the layer below it.

Atoms in BCC arrangements are much more efficiently packed than in a simple cubic structure, occupying about 68% of the total volume. Isomorphous metals with a BCC structure include K, Ba, Cr, Mo, W, and Fe at room temperature. (Elements or compounds that crystallize with the same structure are said to be isomorphous.)

Face-Centered Cubic Cells

Many other metals, such as aluminum, copper, and lead, crystallize in an arrangement that has a cubic unit cell with atoms at all of the corners and at the centers of each face, as illustrated in Figure 3. This arrangement is called a face-centered cubic (FCC) solid. A FCC unit cell contains four atoms: one-eighth of an atom at each of the eight corners (8 × \frac{1}{8} = 1 atom from the corners)) and one-half of an atom on each of the six faces (6 × ½ = 3 atoms from the corners) atoms from the faces). The atoms at the corners touch the atoms in the centers of the adjacent faces along the face diagonals of the cube. Because the atoms are on identical lattice points, they have identical environments.

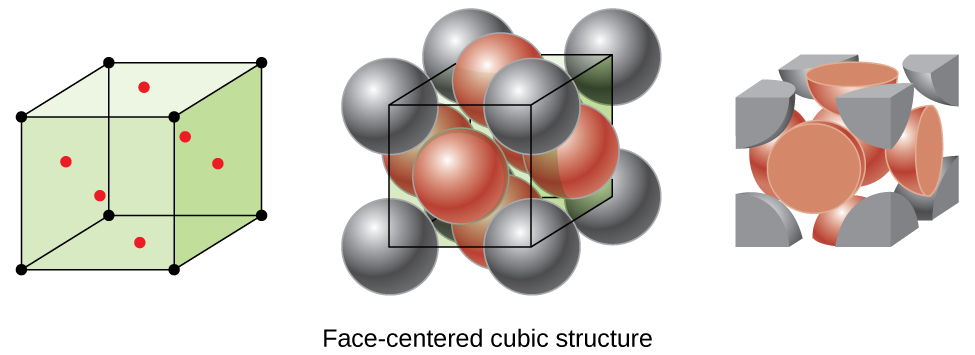
Three images are shown. The first image shows a cube with black dots at each corner and red dots in the center of each face of the cube while the second image is composed of eight spheres that are stacked together to form a cube with six more spheres, one located on each face of the structure. Dots at the center of each corner sphere are connected to form a cube shape. The name under this image reads “Face-centered cubic structure.” The third image is the same as the second, but only shows the portions of the spheres that lie inside the cube shape.
Figure 3. A face-centered cubic solid has atoms at the corners and, as the name implies, at the centers of the faces of its unit cells.

Atoms in an FCC arrangement are packed as closely together as possible, with atoms occupying 74% of the volume. This structure is also called cubic closest packing (CCP). In CCP, there are three repeating layers of hexagonally arranged atoms. Each atom contacts six atoms in its own layer, three in the layer above, and three in the layer below. In this arrangement, each atom touches 12 near neighbors, and therefore has a coordination number of 12. The fact that FCC and CCP arrangements are equivalent may not be immediately obvious, but why they are actually the same structure is illustrated in Figure 4.

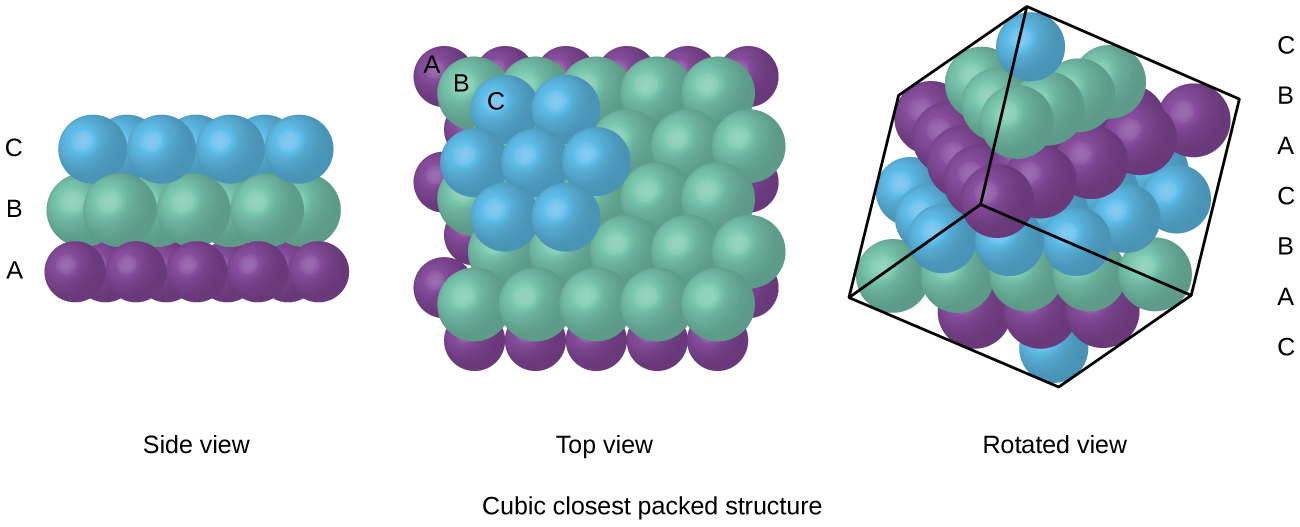
Three images are shown. In the first image, a side view shows a layer of blue spheres, labeled “C” stacked on top of, and sitting in between the gaps in a second layer that is composed of green spheres, labeled “B,” which are sitting atop a purple layer of spheres labeled “A.” A label below this image reads “Side view.” The second image shows a top view of the same layers of spheres, where the top layer is “C,” the second layer is “B” and the lowest layer is “C.” This image is labeled “Top view” and written under this is the phrase “Cubic closest packed structure.” The third image shows an upper view of the side of a cube composed of two sets of the repeating layers shown in the other images. The layers are arranged “C, B, A, C, B, A, C” and the phrase written under this image reads “Rotated view.”
Figure 4. A CCP arrangement consists of three repeating layers (ABCABC…) of hexagonally arranged atoms. Atoms in a CCP structure have a coordination number of 12 because they contact six atoms in their layer, plus three atoms in the layer above and three atoms in the layer below. By rotating our perspective, we can see that a CCP structure has a unit cell with a face containing an atom from layer A at one corner, atoms from layer B across a diagonal (at two corners and in the middle of the face), and an atom from layer C at the remaining corner. This is the same as a face-centered cubic arrangement.

Because closer packing maximizes the overall attractions between atoms and minimizes the total intermolecular energy, the atoms in most metals pack in this manner.

Example 1

Calculation of Atomic Radius and Density for Metals, Part 2
Calcium crystallizes in a face-centered cubic structure. The edge length of its unit cell is 558.8 pm.

  1. What is the atomic radius of Ca in this structure?
  2. Calculate the density of Ca.

Solution

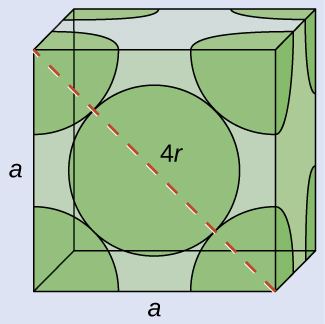
An image of a cube is shown. A one-eighth section of a sphere is shown inside each corner of the cube and a full sphere is shown in the middle of the cube. A line stretched across the front face of the cube from the top left corner to the bottom right corner is labeled “4 r.” The left and bottom sides of the cube are labeled “a.”

(a) In an FCC structure, Ca atoms contact each other across the diagonal of the face, so the length of the diagonal is equal to four Ca atomic radii (d = 4r). Two adjacent edges and the diagonal of the face form a right triangle, with the length of each side equal to 558.8 pm and the length of the hypotenuse equal to four Ca atomic radii:

a2 + a2 = d2  →  (558.8 pm)2 + (558.8 pm)2 = (4r)2

Solving this gives a Ca radius of

r = \sqrt{\dfrac{(558.8\;\text{pm})^2 + (558.8\;\text{pm})^2}{16}} = 197.6 pm

(b) Density is given by density = \dfrac{\text{mass}}{\text{volume}}. The density of calcium can be found by determining the density of its unit cell: for example, the mass contained within a unit cell divided by the volume of the unit cell. A face-centered Ca unit cell has one-eighth of an atom at each of the eight corners (8 × \frac{1}{8} = 1atom) and one-half of an atom on each of the six faces (6 × ½ = 3), for a total of four atoms in the unit cell.

The mass of the unit cell can be found by:

1 Ca unit cell × \dfrac{4\;\text{Ca atoms}}{1\;\text{Ca unit cell}} \times \dfrac{1\;\text{mol Ca}}{6.022 \times 10^{23}\;\text{Ca atoms}} \times \dfrac{40.078\;\text{g}}{1\;\text{mol Ca}} = 2.662 × 10-22 g

The volume of a Ca unit cell can be found by:

V = a3 = (558.8 × 10-10 cm)3 = 1.745 × 10-22 cm3

(Note that the edge length was converted from pm to cm to get the usual volume units for density.) Then,

Density of Ca = \dfrac{2.662 \times 10^{-22}\;\text{g}}{1.745 \times 10^{-22}\;\text{cm}^{3}} = 1.53 g/cm3

Check Your Learning
Silver crystallizes in an FCC structure. The edge length of its unit cell is 409 pm.

  1. What is the atomic radius of Ag in this structure?
  2. Calculate the density of Ag.

Answer:

(a) 145 pm;  (b) 10.5 g/cm3

Summary of Cubic Unit Cells

Primitive Cubic (PC) Body-Centered Cubic (BCC) Face-Centered Cubic (FCC)
Atoms per unit cell 1 2 4
Coordination number 6 8 12
Atom radius (r) and cell length (l) 2r = l \sqrt{3} × l = 4r \sqrt{2} × l = 4r
Packing efficiency 52% 68% 74%

Key Concepts and Summary

The structures of crystalline metals and simple ionic compounds can be described in terms of packing of spheres. Metal atoms can pack in primitive cubic, body-centered cubic, and face-centered cubic structures. Each packing has its own characteristics with respect to the volume occupied by the atoms and the closeness of the packing.

Glossary

body-centered cubic (BCC) solid
crystalline structure that has a cubic unit cell with lattice points at the corners and in the center of the cell
body-centered cubic unit cell
simplest repeating unit of a body-centered cubic crystal; it is a cube containing lattice points at each corner and in the center of the cube
cubic closest packing (CCP)
crystalline structure in which planes of closely packed atoms or ions are stacked as a series of three alternating layers of different relative orientations (ABC)
face-centered cubic (FCC) solid
crystalline structure consisting of a cubic unit cell with lattice points on the corners and in the center of each face
face-centered cubic unit cell
simplest repeating unit of a face-centered cubic crystal; it is a cube containing lattice points at each corner and in the center of each face
isomorphous
possessing the same crystalline structure

Chemistry End of Section Exercises

  1. What is the coordination number of a chromium atom in the body-centered cubic structure of chromium?
  2. What is the coordination number of an aluminum atom in the face-centered cubic structure of aluminum?
  3. Tungsten crystallizes in a body-centered cubic unit cell with an edge length of 3.165 Å.
    1. What is the atomic radius of tungsten in this structure?
    2. Calculate the density of tungsten.
  4. Platinum (atomic radius = 1.38 Å) crystallizes in a cubic closely packed structure. Calculate the edge length of the face-centered cubic unit cell and the density of platinum.
  5. Barium crystallizes in a body-centered cubic unit cell with an edge length of 5.025 Å
    1. What is the atomic radius of barium in this structure?
    2. Calculate the density of barium.
  6. Aluminum (atomic radius = 1.43 Å) crystallizes in a cubic closely packed structure. Calculate the edge length of the face-centered cubic unit cell and the density of aluminum.

Answers to Chemistry End of Section Exercises

  1. eight
  2. twelve
  3. (a) 1.370 Å;  (b) 19.26 g/cm3
  4. edge length: 3.903 Å;  density: 21.79 g/cm3
  5. (a) 2.176 Å;  (b) 3.595 g/cm3
  6. edge length: 4.045 Å;  density: 2.709 g/cm3
Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 103/104 Resource Book Copyright © by Chem 103 Textbook Team and Chem 104 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.