M1Q0b: Accuracy, Precision, and Significant Figures
Introduction
This section explores accuracy, precision, and significant figures. This section includes worked examples, sample problems, and a glossary.
Learning Objectives for Accuracy, Precision, and Significant Figures:
- Differentiate between accuracy and precision.
| Accuracy and Precision | - Properly employ significant figures in measurements and calculations.
| Significant Figures in Measurements | Significant Figures in Calculations |
| Key Concepts and Summary | Glossary | End of Section Exercises |
Accuracy and Precision
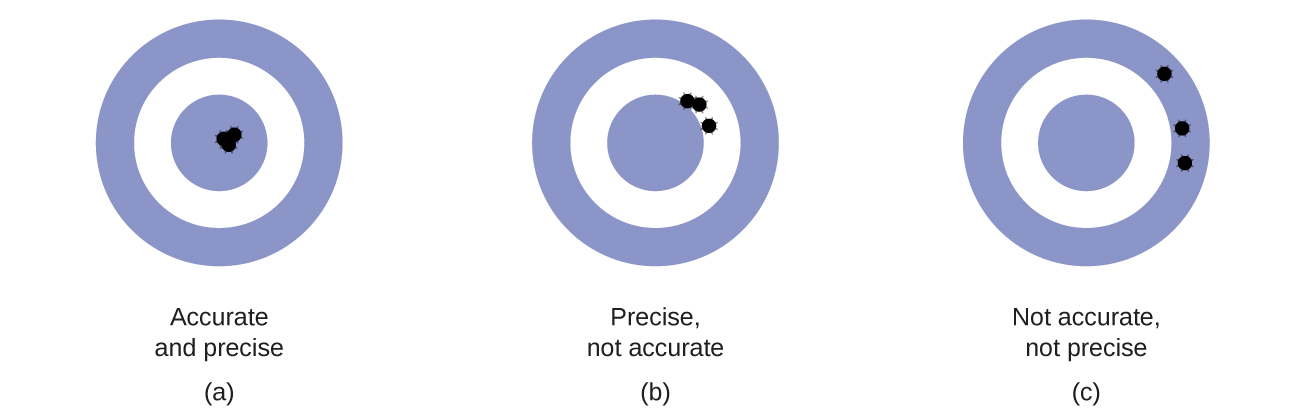
Scientists typically make repeated measurements of a quantity to ensure the quality of their findings and to know both the precision and the accuracy of their results. Measurements are said to be precise if they yield very similar results when repeated in the same manner. A measurement is considered accurate if it yields a result that is very close to the true or accepted value. Precise values agree with each other; accurate values agree with a true value. These characterizations can be extended to other contexts, such as the results of an archery competition (Figure 1).
Counting is the only type of measurement that is free from uncertainty, provided the number of objects being counted is not extremely large. The result of such a counting measurement is an example of an exact number. For example, if we count eggs in a carton, we know exactly how many eggs the carton contains. Quantities derived from measurements other than counting, however, are uncertain to varying extents due to practical limitations of the measurement process used.
The numbers of defined quantities are also exact. By definition, 1 foot is exactly 12 inches, 1 inch is exactly 2.54 centimeters, and 1 gram is exactly 0.001 kilogram.
Significant Figures in Measurements
Measured quantities, unlike defined or directly counted quantities, are not exact. In the laboratory, you will need to understand the limitations of the measuring devices you will use, such as balances and graduated cylinders. For example, when measuring the volume of liquid in a graduated cylinder, you should make a reading at the bottom of the meniscus, the lowest point on the curved surface of the liquid.
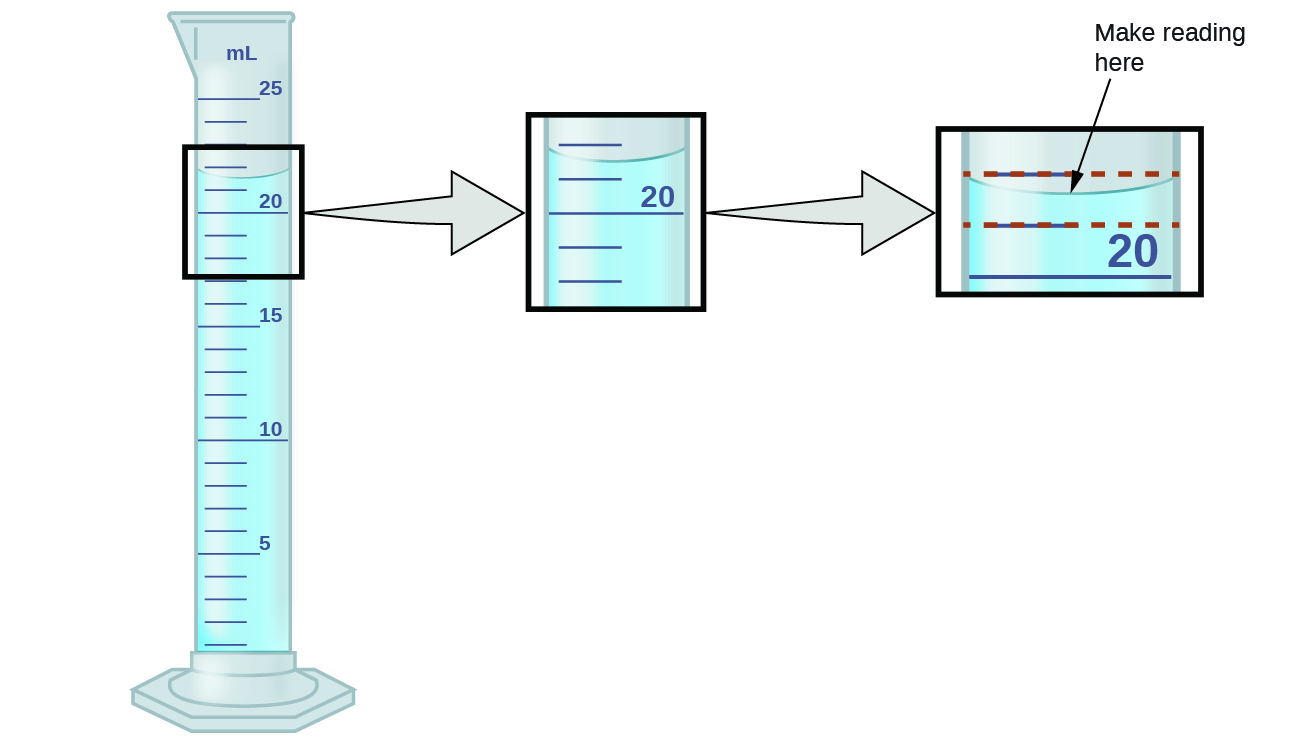
Refer to the illustration in Figure 2. The bottom of the meniscus in this case clearly lies between the 21 and 22 markings, meaning the liquid volume is certainly greater than 21 mL but less than 22 mL. The meniscus appears to be a bit closer to the 22-mL mark than to the 21-mL mark, and so a reasonable estimate of the liquid’s volume would be 21.6 mL. Therefore, in the number 21.6, the digits 2 and 1 are certain, but the 6 is an estimate. Some people might estimate the meniscus position to be equally distant from each of the markings and estimate the tenth-place digit as 5, while others may think it to be even closer to the 22-mL mark and estimate the tenth-place digit to be 7. Note that it would be pointless to attempt to estimate a digit for the hundredths place, given that the tenths-place digit is uncertain. In general, numerical scales such as the one on this graduated cylinder will permit measurements to one-tenth of the smallest scale division. The scale in this case has 1-mL divisions, and so volumes may be measured to the nearest 0.1 mL.
This concept holds true for all measurements, even if you do not actively make an estimate. If you place a quarter on a standard electronic balance, you may obtain a reading of 6.72 g. The digits 6 and 7 are certain, and the 2 indicates that the mass of the quarter is likely between 6.71 and 6.73 grams. The quarter weighs about 6.72 grams, with a nominal uncertainty in the measurement of ± 0.01 gram. If we weigh the quarter on a more sensitive balance, we may find that its mass is 6.723 g. This means its mass lies between 6.722 and 6.724 grams, an uncertainty of 0.001 gram. Every measurement has some uncertainty, which depends on the device used (and the user’s ability). All of the digits in a measurement, including the uncertain last digit, are called significant figures or significant digits. Note that zero may be a measured value; for example, if you stand on a scale that shows weight to the nearest pound and it shows “120,” then the 1 (hundreds), 2 (tens) and 0 (ones) are all significant (measured) values.
Whenever you make a measurement properly, all the digits in the result are significant. But what if you were analyzing a reported value and trying to determine what is significant and what is not? Well, for starters, all nonzero digits are significant, and it is only zeros that require some thought. We will use the terms “leading,” “trailing,” and “captive” for the zeros of a value and will consider how to deal with them.
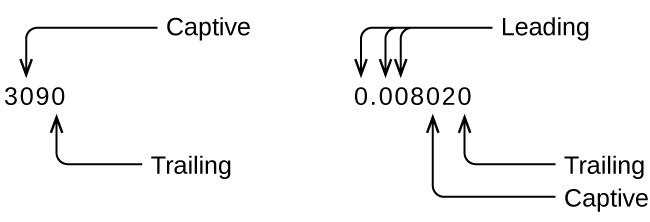
Starting with the first nonzero digit on the left, count this digit and all remaining digits to the right. This is the number of significant figures in the measurement unless the last digit is a trailing zero lying to the left of the decimal point.

Captive zeros result from measurement and are therefore always significant. Leading zeros, however, are never significant—they merely tell us where the decimal point is located.

The leading zeros in the last example are not significant. We can instead use exponential notation (as described in Appendix B) and express the number as 8.32407 × 10−3, then the number 8.32407 contains all of the significant figures, and 10−3 locates the decimal point.
The number of significant figures is uncertain in a number that ends with a zero to the left of the decimal point location. The zeros in the measurement 1,300 grams could be significant or they could simply indicate where the decimal point is located. The ambiguity can be resolved with the use of exponential notation: 1.3 × 103 (two significant figures), 1.30 × 103 (three significant figures, if the tens place was measured), or 1.300 × 103 (four significant figures, if the ones place was also measured). In cases where only the decimal-formatted number is available, it is prudent to assume that all trailing zeros are not significant.
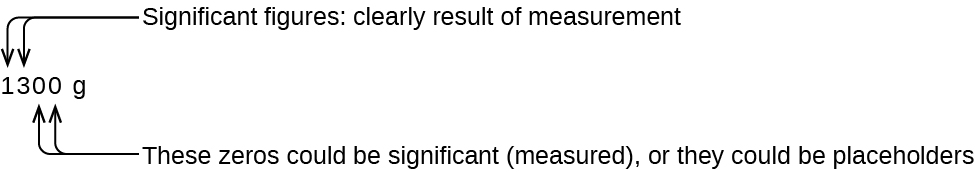
When determining significant figures, be sure to pay attention to reported values and think about the measurement and significant figures in terms of what is reasonable or likely when evaluating whether the value makes sense. For example, the official 2020 census reported the resident population of the US as 331,449,281 as of April 1, 2020. Do you think the US population was correctly determined to the reported nine significant figures, that is, to the exact number of people? People are constantly being born, dying, or moving into or out of the country, and assumptions are made to account for the large number of people who are not actually counted. Because of these uncertainties, it might be more reasonable to expect that we know the population to within perhaps a million or so, in which case the population should be reported as 3.31 × 108 people.
Significant Figures in Calculations
A second important principle of uncertainty is that results calculated from a measurement are at least as uncertain as the measurement itself. We must take the uncertainty in our measurements into account to avoid misrepresenting the uncertainty in calculated results. One way to do this is to report the result of a calculation with the correct number of significant figures, which is determined by the following three rules for rounding numbers:
- When we add or subtract numbers, we should round the result to the same number of decimal places as the number with the least number of decimal places (the least precise value in terms of addition and subtraction).
- When we multiply or divide numbers, we should round the result to the same number of digits as the number with the least number of significant figures (the least precise value in terms of multiplication and division).
- If the digit to be dropped (the one immediately to the right of the digit to be retained) is less than 5, we “round down” and leave the retained digit unchanged; if it is more than 5, we “round up” and increase the retained digit by 1. If the dropped digit is 5, we round up or down, whichever yields an even value for the retained digit. (The last part of this rule may strike you as a bit odd, but it’s based on reliable statistics and is aimed at avoiding any bias when dropping the digit “5,” since it is equally close to both possible values of the retained digit.)
The following examples illustrate the application of this rule in rounding a few different numbers to three significant figures:
- 0.028675 rounds “up” to 0.0287 (the dropped digit, 7, is greater than 5)
- 18.3384 rounds “down” to 18.3 (the dropped digit, 3, is less than 5)
- 6.8752 rounds “up” to 6.88 (the dropped digit is 5, and the retained digit is even)
- 92.85 rounds “down” to 92.8 (the dropped digit is 5, and the retained digit is even)
Let’s work through these rules with a few examples.
Example 1
Rounding Numbers
Round the following to the indicated number of significant figures:
- 31.57 (to two significant figures)
- 8.1649 (to three significant figures)
- 0.051065 (to four significant figures)
- 0.90275 (to four significant figures)
Solution
- 31.57 rounds “up” to 32 (the dropped digit is 5, and the retained digit is even)
- 8.1649 rounds “down” to 8.16 (the dropped digit, 4, is less than 5)
- 0.051065 rounds “down” to 0.05106 (the dropped digit is 5, and the retained digit is even)
- 0.90275 rounds “up” to 0.9028 (the dropped digit is 5, and the retained digit is even)
Check Your Learning
Round the following to the indicated number of significant figures:
- 0.424 (to two significant figures)
- 0.0038661 (to three significant figures)
- 421.25 (to four significant figures)
- 28,683.5 (to five significant figures)
Answer:
(a) 0.42; (b) 0.00387; (c) 421.2; (d) 28,684
Example 2
Addition and Subtraction with Significant Figures
Rule: When we add or subtract numbers, we should round the result to the same number of decimal places as the number with the least number of decimal places (i.e., the least precise value in terms of addition and subtraction).
- Add 1.0023 g and 4.383 g.
- Subtract 421.23 g from 486 g.
Solution
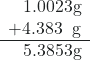
Answer is 5.385 g (round to the thousandths place; three decimal places)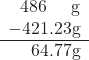
Answer is 65 g (round to the ones place; no decimal places)

Check Your Learning
- Add 2.334 mL and 0.31 mL.
- Subtract 55.8752 m from 56.533 m.
Answer:
(a) 2.64 mL; (b) 0.658 m
Example 3
Multiplication and Division with Significant Figures
Rule: When we multiply or divide numbers, we should round the result to the same number of digits as the number with the least number of significant figures (the least precise value in terms of multiplication and division).
- Multiply 0.6238 cm by 6.6 cm.
- Divide 421.23 g by 486 mL.
Solution
- 0.6238 cm × 6.6 cm = 4.11708 cm2
→ result is 4.1 cm2 (round to two significant figures)- four significant figures × two significant figures
→ two significant figures in answer
- four significant figures × two significant figures
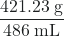 = 0.86728 g/mL
= 0.86728 g/mL
→ result is 0.867 g/mL (round to three significant figures)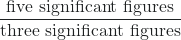
→ three significant figures in answer
Check Your Learning
- Multiply 2.334 cm and 0.320 cm.
- Divide 55.8752 m by 56.53 s.
Answer:
(a) 0.747 cm2 (b) 0.9884 m/s
In the midst of all these technicalities, it is important to keep in mind the reason why we use significant figures and rounding rules—to correctly represent the certainty of the values we report and to ensure that a calculated result is not represented as being more certain than the least certain value used in the calculation.
Quantities can be exact or measured. Measured quantities have an associated uncertainty that is represented by the number of significant figures in the measurement. The uncertainty of a calculated value depends on the uncertainties in the values used in the calculation and is reflected in how the value is rounded. Measured values can be accurate (close to the true value) and/or precise (showing little variation when measured repeatedly).
Example 4
Calculation of Volume and Density with Significant Figures
One common bathtub is 13.44 dm long, 5.920 dm wide, and 2.54 dm deep. Assume that the tub is rectangular and calculate its approximate volume in liters.
Solution
| V | = | l × w × d |
| = | 13.44 dm × 5.920 dm × 2.54 dm | |
| = | 202.09459 dm3 (value from calculator) | |
| = | 202 dm3 or 202 L (answer rounded to three significant figures) |
Check Your Learning
What is the density of a liquid with a mass of 31.1415 g and a volume of 30.13 cm3?
Answer:
1.034 g/mL
Example 5
Experimental Determination of Density Using Water Displacement
A piece of rebar is weighed and then submerged in a graduated cylinder partially filled with water, with results as shown.
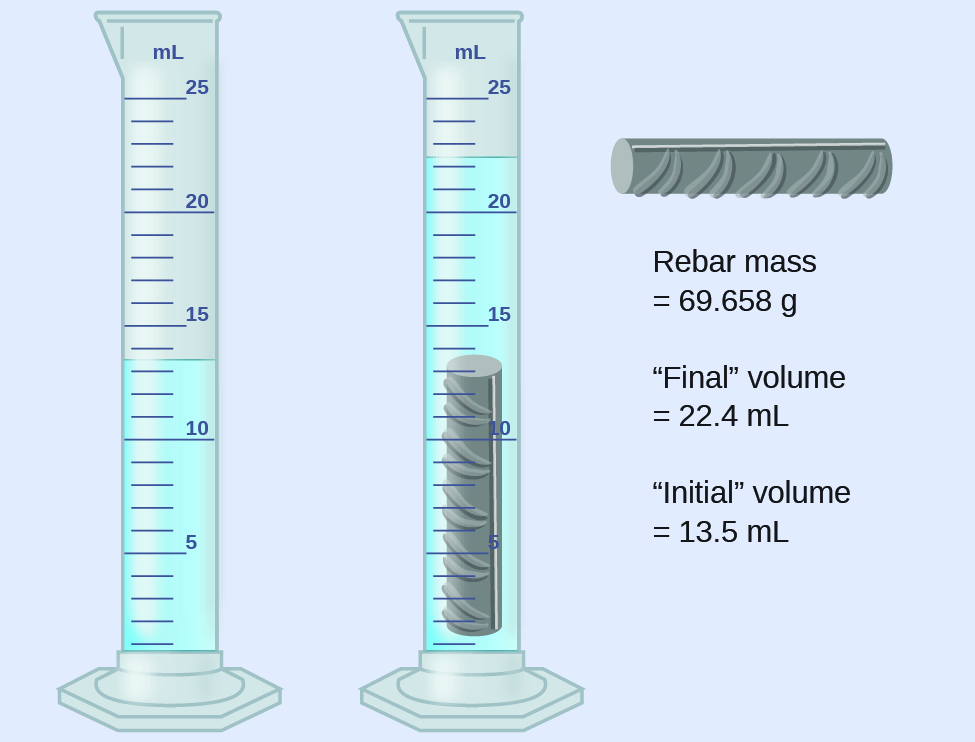
- Use these values to determine the density of this piece of rebar.
- Rebar is mostly iron. Does your result in (a) support this statement? How?
Solution
The volume of the piece of rebar is equal to the volume of the water displaced:
volume = 22.4 mL – 13.5 mL = 8.9 mL = 8.9 cm3
(rounded to the nearest 0.1 mL, per the rule for addition and subtraction)
The density is the mass-to-volume ratio:
density = ![]() = 7.8 g/cm3
= 7.8 g/cm3
(rounded to two significant figures, per the rule for multiplication and division)
The density of iron is 7.9 g/cm3, very close to that of rebar, which lends some support to the fact that rebar is mostly iron.
Check Your Learning
An irregularly shaped piece of a shiny yellowish material is weighed and then submerged in a graduated cylinder, with results as shown.

- Use these values to determine the density of this material.
- Do you have any reasonable guesses as to the identity of this material? Explain your reasoning.
Answer:
(a) 19 g/cm3
(b) It is likely gold because it has the right appearance for gold and is very close to the density given for gold in Table 3.
Key Concepts and Summary
Significant figures are used to correctly represent the certainty of the values we report and calculate. Measured quantities have an associated uncertainty that is represented by the number of significant figures in the measurement. The uncertainty of a calculated value depends on the uncertainties in the values used in the calculation and is reflected in how the value is rounded. Measured values can be accurate (close to the true value) and/or precise (showing little variation when measured repeatedly).
Glossary
- accuracy
- how closely a measurement aligns with a correct value
- exact number
- number derived by counting or by definition
- precision
- how closely a measurement matches the same measurement when repeated
- rounding
- procedure used to ensure that calculated results properly reflect the uncertainty in the measurements used in the calculation
- significant figures
- (also, significant digits) all of the measured digits in a determination, including the uncertain last digit
- uncertainty
- estimate of amount by which measurement differs from true value
Chemistry End of Section Exercises
- Determine how many significant figures are in each of the following numbers and then rewrite each number in scientific notation:
- 704
- 0.03344
- 5000
- 22080
- 1000.00
- 0.0000000651
- 0.00007157
- 0.04500
- Categorize each of the following as either an exact number or a measurement:
- the number of eggs in a basket
- the mass of a dozen eggs
- the number of gallons of gasoline necessary to fill an automobile gas tank
- the number of cm in 2 m
- the volume of a can of soda
- the time required to drive from San Francisco to Kansas City at an average speed of 53 mi/h
- Perform the following calculations and report each answer with the correct number of significant figures.
- 628 × 342
- (5.63 × 102) × (7.4 × 103)
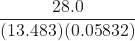
- 8119 × 0.000023
- 14.98 + 27,342 + 84.7593
- 42 + 0.2599
- 0.147 + 0.0066 + 0.002
- 15 – 0.15 – 0.6155
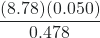
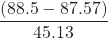
- Consider the results of the archery contest shown in this figure.
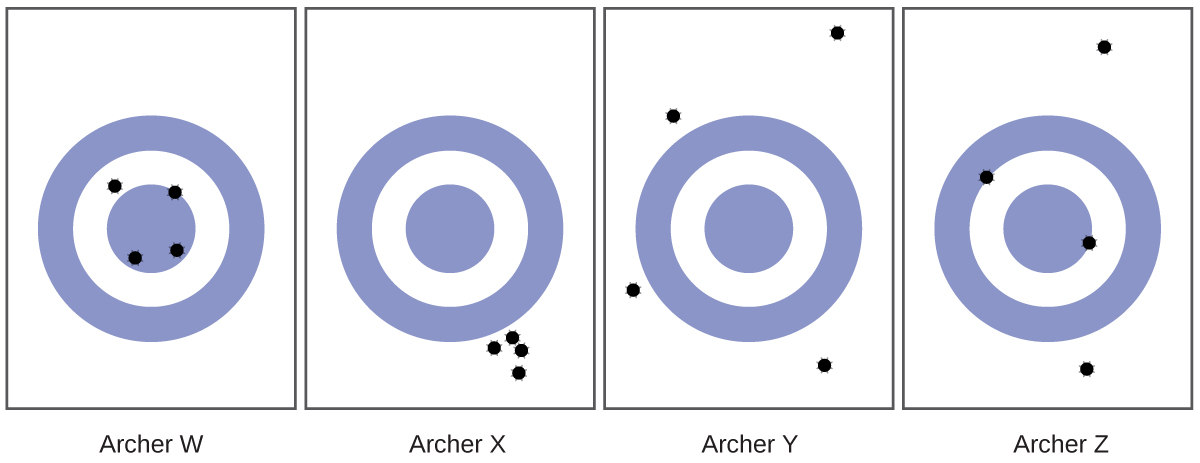
- Which archer is most precise?
- Which archer is most accurate?
- Who is both least precise and least accurate?
- Classify the following sets of measurements as accurate, precise, both, or neither.
- Use different balances to weight a metal square with a known mass of 15.000 g: 17.27 g, 13.05 g, 19.46 g, 16.92 g
- Testing the volume of a batch of 25-mL pipettes: 27.02 mL, 26.99 mL, 26.97 mL, 27.01 mL
- Determining the purity of a pure gold sample: 99.9999%, 99.9998%, 99.9998%, 99.9999%
- A large piece of jewelry has a mass of 132.6 g. A graduated cylinder initially contains 48.6 mL water. When the jewelry is submerged in the graduated cylinder, the total volume increases to 61.2 mL.
- Determine the density of this piece of jewelry.
- Assuming that the jewelry is made from only one substance, what substance is it likely to be? The following information may be helpful:
Substance Density Diamond 3.51 g/cm3 Gold 19.3 g/cm3 Platinum 21.5 g/cm3 Silver 10.5 g/cm3
Answers to Chemistry End of Section Exercises
- (a) 3 significant figures, 7.04 × 102
(b) 4 significant figures, 3.344 × 10−2
(c) 1 significant figures, 5 × 103
(d) 4 significant figures, 2.208 × 104
(e) 6 significant figures, 1.00000 × 103
(f) 3 significant figures, 6.51 × 10−8
(g) 4 significant figures, 7.157 × 10−5
(h) 4 significant figures, 4.500 × 10-2 - (a) exact
(b) measured
(c) measured
(d) exact
(e) measured
(f) measured - (a) 2.15 × 105
(b) 4.2 × 106
(c) 35.6
(d) 0.19
(e) 27,442
(f) 42
(g) 0.156
(h) 14
(i) 0.92
(j) 0.02 - (a) Archer X; (b) Archer W; (c) Archer Y
- (a) Not accurate or precise
(b) Precise but not accurate
(c) Precise and accurate - (a) 10.5 g/cm3; (b) silver
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

