M1Q0a: Measurements, Units, Density
Introduction
The section explores measurement, the standard units of science, and density. This section includes worked examples, sample problems, and a glossary.
Learning Objectives for Measurements, Units, Density:
- Identify and use the prefixes, units of measurement, and conversions in chemistry.
| Prefixes | SI Base Units | - Relate mass, volume, and density of a substance.
| Density | - Compare properties of matter
| Intensive and Extensive Properties |
| Key Concepts and Summary | Key Equations | Glossary | End of Section Exercises |
Measurements
Measurements provide the macroscopic information that is the basis of most hypotheses, theories, and laws that describe the behavior of matter and energy in both the macroscopic and microscopic domains of chemistry. Every measurement provides three kinds of information: the size or magnitude of the measurement (a number); a standard of comparison for the measurement (a unit); and an indication of the uncertainty of the measurement. While the number and unit are explicitly represented when a quantity is written, the uncertainty is an aspect of the measurement result that is more implicitly represented and will be discussed later.
The number in the measurement can be represented in different ways, including decimal form and scientific notation. (Scientific notation is also known as exponential notation; a review of this topic can be found in Appendix B). For example, the maximum takeoff weight of a Boeing 777-200ER airliner is 298,000 kilograms, which can also be written as 2.98 × 105 kg. The average mass of a mosquito is about 0.0000025 kilograms, which can be written as 2.5 × 10−6 kg.
Units, such as liters, pounds, and centimeters, are standards of comparison for measurements. When we buy a 2 liter bottle of a soft drink, we expect that the volume of the drink was measured, so it is two times larger than the volume that everyone agrees to be 1 liter. The meat used to prepare a 0.25 pound hamburger is measured so it weighs one-fourth as much as 1 pound. Without units, a number can be meaningless, confusing, or possibly life threatening. Suppose a doctor prescribes phenobarbital to control a patient’s seizures and states a dosage of “100” without specifying units. Not only will this be confusing to the medical professional giving the dose, but the consequences can be dire: 100 mg given three times per day can be effective as an anticonvulsant, but a single dose of 100 g is more than 10 times the lethal amount.
We usually report the results of scientific measurements in SI units, an updated version of the metric system, using the units listed in Table 1. Other units can be derived from these base units. The standards for these units are fixed by international agreement, and they are called the International System of Units or SI Units (from the French, Le Système International d’Unités). SI units have been used by the United States National Institute of Standards and Technology (NIST) since 1964.
| Property Measured | Name of Unit | Symbol of Unit |
| length | meter | m |
| mass | kilogram | kg |
| time | second | s |
| temperature | kelvin | K |
| electric current | ampere | A |
| amount of substance | mole | mol |
| luminous intensity | candela | cd |
Sometimes we use units that are fractions or multiples of a base unit. Ice cream is sold in quarts (a familiar, non-SI base unit), pints (0.5 quart), or gallons (4 quarts). We also use fractions or multiples of units in the SI system, but these fractions or multiples are always powers of 10. Fractional or multiple SI units are named using a prefix and the name of the base unit. For example, a length of 1000 meters is also called a kilometer because the prefix kilo means “one thousand,” which in scientific notation is 103 (1 kilometer = 1000 m = 103 m). The prefixes used and the powers to which 10 are raised are listed in Table 2.

Need a refresher or more practice with scientific notation? Visit this site to go over basics of scientific notation.
SI Base Units
The initial units of the metric system, which eventually evolved into the SI system, were established in France during the French Revolution. The original standards for the meter and the kilogram were adopted there in 1799 and eventually by other countries. This section introduces four of the SI base units commonly used in chemistry. Other SI units will be introduced in subsequent chapters.
Length
The standard unit of length in both the SI and original metric systems is the meter (m). A meter was originally specified as 1/10,000,000 of the distance from the North Pole to the equator. It is now defined as the distance light in a vacuum travels in 1/299,792,458 of a second. A meter is about 3 inches longer than a yard (Figure 1); one meter is about 39.37 inches or 1.094 yards. Longer distances are often reported in kilometers (1 km = 1000 m = 103 m), whereas shorter distances can be reported in centimeters (1 cm = 0.01 m = 10−2 m) or millimeters (1 mm = 0.001 m = 10−3 m).
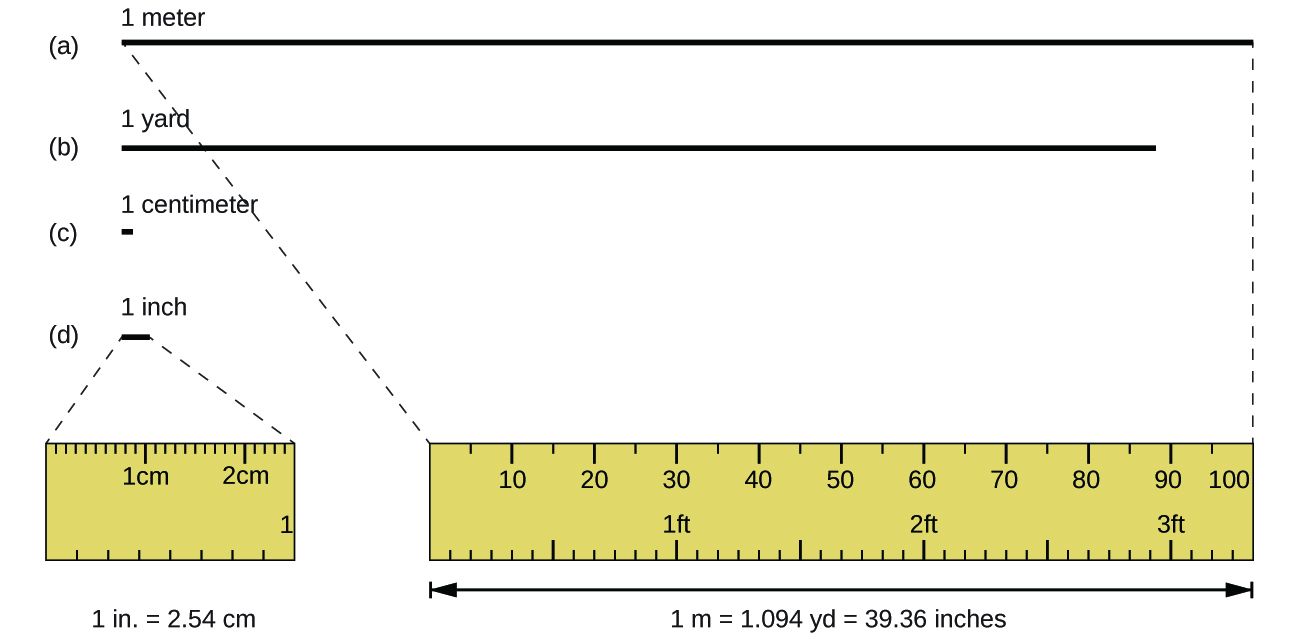
Mass
The standard unit of mass in the SI system is the kilogram (kg). A kilogram was originally defined as the mass of a liter of water (a cube of water with an edge length of exactly 0.1 meter). Until May 2019, the kilogram was defined by a certain cylinder of platinum-iridium alloy, which is kept in France. Any object with the same mass as this cylinder was said to have a mass of 1 kilogram. One kilogram is about 2.2 pounds. The gram (g) is exactly equal to 1/1000 of the mass of the kilogram (10−3 kg). Currently, the kilogram is defined in quantum mechanical terms based on Planck’s constant. Learn about the latest definition of the kilogram.
Time
The SI base unit of time is the second (s). Small and large time intervals can be expressed with the appropriate prefixes; for example, 3 microseconds = 0.000003 s = 3 × 10−6 s and 5 megaseconds = 5,000,000 s = 5 × 106 s. Alternatively, hours, days, and years can be used.
Temperature
Temperature is an intensive property. The SI unit of temperature is the kelvin (K). The IUPAC convention is to use kelvin (all lowercase) for the word, K (uppercase) for the unit symbol, and neither the word “degree” nor the degree symbol (°). The degree Celsius (°C) is also allowed in the SI system, with both the word “degree” and the degree symbol used for Celsius measurements. Celsius degrees are the same magnitude as those of kelvin, but the two scales place their zeros in different places. Water freezes at 273.15 K (0 °C) and boils at 373.15 K (100 °C) by definition, and normal human body temperature is approximately 310 K (37 °C).
Conversion of Temperature Units
We use the word temperature to refer to the hotness or coldness of a substance. One way we measure a change in temperature is to use the fact that most substances expand when their temperature increases and contract when their temperature decreases. The mercury or alcohol in a common glass thermometer changes its volume as the temperature changes. Because the volume of the liquid changes more than the volume of the glass, we can see the liquid expand when it gets warmer and contract when it gets cooler.
Unlike the Celsius scale, the kelvin scale is an absolute temperature scale in which zero kelvin (0 K) corresponds to the lowest temperature that can theoretically be achieved. The early 19th-century discovery of the relationship between a gas’s volume and temperature suggested that the volume of a gas would be zero at −273.15 °C. In 1848, British physicist William Thompson, who later adopted the title of Lord Kelvin, proposed an absolute temperature scale based on this concept (further treatment of this topic is provided later in the Gases Module).
The freezing temperature of water on this scale is 273.15 K and its boiling temperature is 373.15 K. Notice the numerical difference in these two reference temperatures is 100, the same as for the Celsius scale, and so the linear relation between these two temperature scales will exhibit a slope of 1 ![]() . Following the same approach, the equations for converting between the kelvin and Celsius temperature scales are derived to be:
. Following the same approach, the equations for converting between the kelvin and Celsius temperature scales are derived to be:
TK = T°C + 273.15
T°C = TK – 273.15
The 273.15 in these equations has been determined experimentally, so it is not exact. Figure 2 shows the relationship among the three temperature scales.
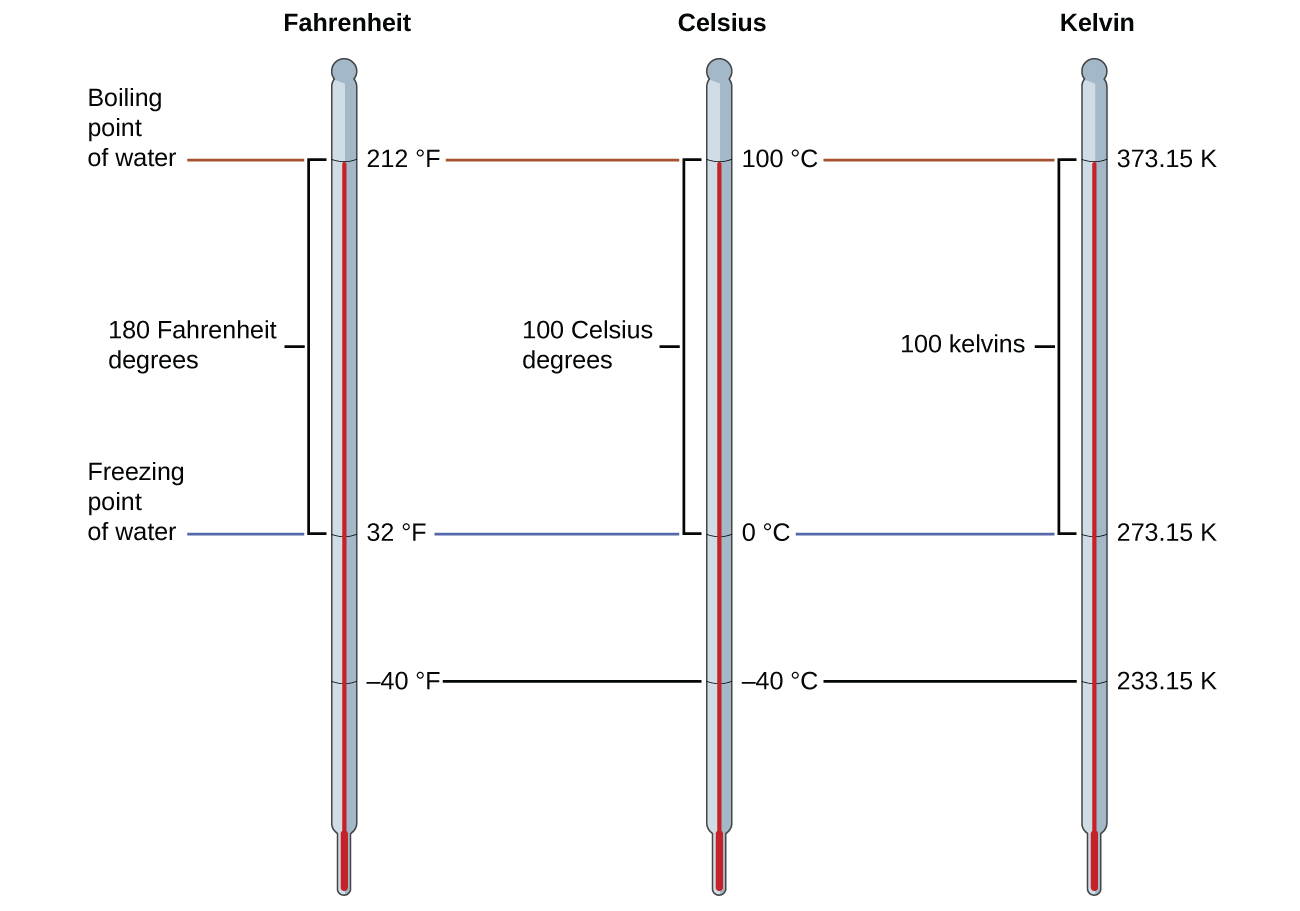
Although the kelvin (absolute) temperature scale is the official SI temperature scale, Celsius is commonly used in many scientific contexts and is the scale of choice for nonscience contexts in almost all areas of the world. Very few countries (the U.S. and its territories, the Bahamas, Belize, Cayman Islands, and Palau) still use Fahrenheit for weather, medicine, and cooking.
Example 1
Conversion from Celsius
Normal body temperature has been commonly accepted as 37.0 °C (although it varies depending on time of day and method of measurement, as well as among individuals). What is this temperature on the kelvin scale and on the Fahrenheit scale?
Solution
K = °C + 273.15 = 37.0 + 273.2 = 310.2 K
°F = ![]() °C + 32.0 = (
°C + 32.0 = (![]() × 37.0) + 32.0 = 66.6 + 32.0 = 98.6 °F
× 37.0) + 32.0 = 66.6 + 32.0 = 98.6 °F
Check Your Learning
Convert 80.92 °C to K.
Answer:
354.07 K
Derived SI Units
We can derive many units from the SI base units. For example, we can use the base unit of length to define a unit of volume, and the base units of mass and length to define a unit of density.
Volume
Volume is the measure of the amount of space occupied by an object. The standard SI unit of volume is defined by the base unit of length (Figure 3). The standard volume is a cubic meter (m3), a cube with an edge length of exactly one meter. To dispense a cubic meter of water, we could build a cubic box with edge lengths of exactly one meter. This box would hold a cubic meter of water or any other substance.
A more commonly used unit of volume is derived from the decimeter (0.1 m, or 10 cm). A cube with edge lengths of exactly one decimeter contains a volume of one cubic decimeter (dm3). A liter (L) is the more common name for the cubic decimeter. One liter is about 1.06 quarts.
A cubic centimeter (cm3) is the volume of a cube with an edge length of exactly one centimeter. The abbreviation cc (for cubic centimeter) is often used by health professionals. A cubic centimeter is also called a milliliter (mL) and is 1/1000 of a liter.
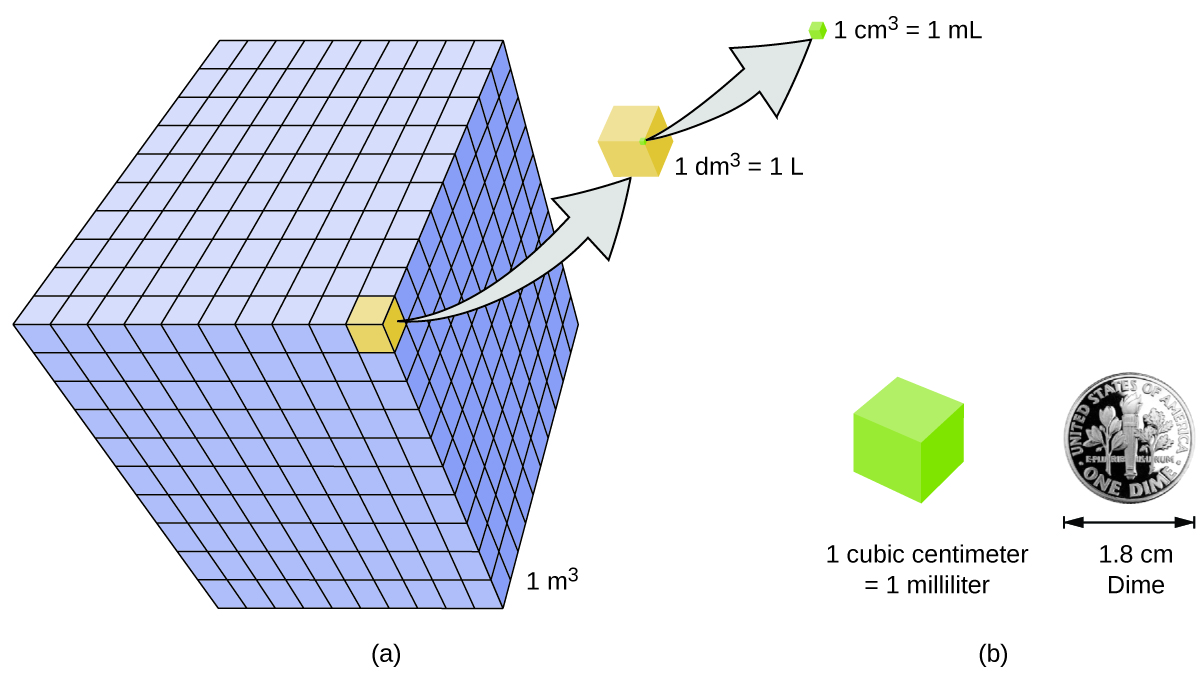
Density
We use the mass and volume of a substance to determine its density. Thus, the units of density are defined by the base units of mass and length.
The density of a substance is the ratio of the mass of a sample of the substance to its volume (mass/volume). The SI unit for density is the kilogram per cubic meter (kg/m3). For many situations, however, this is an inconvenient unit, so we often use grams per cubic centimeter (g/cm3) for the densities of solids and liquids, and grams per liter (g/L) for gases. Although there are exceptions, most liquids and solids have densities that range from about 0.7 g/cm3 (the density of gasoline) to 19 g/cm3 (the density of gold). The density of air is about 1.2 g/L. Table 3 shows the densities of some common substances.
| Solids | Liquids | Gases (at 25 °C and 1 atm) |
|---|---|---|
| ice (at 0 °C) 0.92 g/cm3 | water 1.0 g/cm3 | dry air 1.20 g/L |
| oak (wood) 0.60–0.90 g/cm3 | ethanol 0.79 g/cm3 | oxygen 1.31 g/L |
| iron 7.9 g/cm3 | acetone 0.79 g/cm3 | nitrogen 1.14 g/L |
| copper 9.0 g/cm3 | glycerin 1.26 g/cm3 | carbon dioxide 1.80 g/L |
| lead 11.3 g/cm3 | olive oil 0.92 g/cm3 | helium 0.16 g/L |
| silver 10.5 g/cm3 | gasoline 0.70–0.77 g/cm3 | neon 0.83 g/L |
| gold 19.3 g/cm3 | mercury 13.6 g/cm3 | radon 9.1 g/L |
While there are many ways to determine the density of an object, perhaps the most straightforward method involves separately finding the mass and volume of the object, and then dividing the mass of the sample by its volume. In the following example, the mass is found directly by weighing, but the volume is found indirectly through length measurements.
density = ![]()
Example 2
Calculation of Density
Gold—in bricks, bars, and coins—has been a form of currency for centuries. In order to swindle people into paying for a brick of gold without actually investing in a brick of gold, people have considered filling the centers of hollow gold bricks with lead to fool buyers into thinking that the entire brick is gold. It does not work: lead is a dense substance, but its density is not as great as that of gold, 19.3 g/cm3. What is the density of lead if a cube of lead has an edge length of 2.00 cm and a mass of 90.7 g?
Solution
The density of a substance can be calculated by dividing its mass by its volume. The volume of a cube is calculated by cubing the edge length.
volume of lead cube = 2.00 cm × 2.00 cm × 2.00 cm = 8.00 cm3
density = ![]() = 11.3 g/cm3
= 11.3 g/cm3
(We will discuss the reason for rounding to the first decimal place in the next section.)
Check Your Learning
- To three decimal places, what is the volume of a cube (cm3) with an edge length of 0.843 cm?
- If the cube in part (a) is copper and has a mass of 5.34 g, what is the density of copper to two decimal places?
Answer:
(a) 0.599 cm3 (b) 8.91 g/cm3
Intensive and Extensive Properties
Properties of matter fall into one of two categories. If the property depends on the amount of matter present, it is an extensive property. The mass and volume of a substance are examples of extensive properties; for instance, a gallon of milk has a larger mass and volume than a cup of milk. The value of an extensive property is directly proportional to the amount of matter in question. If the property of a sample of matter does not depend on the amount of matter present, it is an intensive property. Temperature is an example of an intensive property. If the gallon and cup of milk are each at 20 °C (room temperature), when they are combined, the temperature remains at 20 °C. As another example, consider the distinct but related properties of heat and temperature. A drop of hot cooking oil spattered on your arm causes brief, minor discomfort, whereas a pot of hot oil yields severe burns. Both the drop and the pot of oil are at the same temperature (an intensive property), but the pot clearly contains much more heat (extensive property).
Key Concepts and Summary
Measurements provide quantitative information that is critical in studying and practicing chemistry. Each measurement has an amount, a unit for comparison, and an uncertainty. Measurements can be represented in either decimal or scientific notation. Scientists primarily use the SI (International System) or metric systems. We use base SI units such as meters, seconds, and kilograms, as well as derived units, such as liters (for volume) and g/cm3 (for density). In many cases, we find it convenient to use unit prefixes that yield fractional and multiple units, such as microseconds (10−6 seconds) and megahertz (106 hertz).
Key Equations
- density =
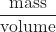
Glossary
- Celsius (°C)
- unit of temperature; water freezes at 0 °C and boils at 100 °C on this scale
- cubic centimeter (cm3 or cc)
- volume of a cube with an edge length of exactly 1 cm
- cubic meter (m3)
- SI unit of volume
- density
- ratio of mass to volume for a substance or object
- extensive property
- property of a substance that depends on the amount of the substance
- intensive property
- property of a substance that is independent of the amount of the substance
- kelvin (K)
- SI unit of temperature; 273.15 K = 0 ºC
- kilogram (kg)
- standard SI unit of mass; 1 kg = approximately 2.2 pounds
- length
- measure of one dimension of an object
- liter (L)
- (also, cubic decimeter) unit of volume; 1 L = 1,000 cm3
- meter (m)
- standard metric and SI unit of length; 1 m = approximately 1.094 yards
- milliliter (mL)
- 1/1,000 of a liter; equal to 1 cm3
- second (s)
- SI unit of time
- SI units (International System of Units)
- standards fixed by international agreement in the International System of Units (Le Système International d’Unités)
- unit
- standard of comparison for measurements
- volume
- amount of space occupied by an object
Chemistry End of Section Exercises
- Explain the difference between extensive properties and intensive properties.
- Identify the following properties as either extensive or intensive.
- volume
- temperature
- humidity
- energy
- boiling point
- density
- Fill in the blanks in the following table:
Prefix Symbol Factor centi- 103 m 10-9 pico- μ - The distance between the centers of the two oxygen atoms in an oxygen molecule is 1.21 × 10−8 cm. What is this distance in nanometers?
- True or False: One carbon atom has a radius of 0.0914 nm. This is equal to 9.14 × 107 m.
- An instructor is preparing for an experiment requiring 225 g phosphoric acid. The only container readily available is a 150-mL Erlenmeyer flask. Is it large enough to contain the acid, whose density is 1.83 g/mL?
- Osmium is one of the densest elements known. What is its density if 2.72 g has a volume of 0.121 cm3?
Answers to Chemistry End of Section Exercises
- The value of an extensive property depends upon the amount of matter being considered, whereas the value of an intensive property is the same regardless of the amount of matter being considered.
- (a) extensive
(b) intensive
(c) intensive
(d) extensive
(e) intensive
(f) intensive (Density is the ratio of mass to volume, both extensive properties, however dividing one extensive property by another will in effect “cancel” this dependence on amount, yielding a ratio that is independent of amount.) -
Prefix Symbol Factor centi- c 10-2 kilo- k 103 milli- m 10-3 nano- n 10-9 pico- p 10-12 micro- μ 10-6 - 0.121 nm
- False
- Yes, the acid’s volume is 123 mL.
- 22.5 g/cm3
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

