M17Q4: Gibbs Free Energy

Chem 103 Textbook Team; Chem 104 Textbook Team

M17Q4: Gibbs Free Energy

Learning Objectives

Derive the relationship between ΔG, ΔS, and ΔH.
Determine ΔG, ΔS, and ΔH qualitatively for selected chemical and physical processes, and predict if these processes are product-favored or reactant-favored.
Predict how temperature affects whether a reaction is product-favored or reactant-favored.
| Temperature and Entropy |
Identify if a given chemical or physical process is driven thermodynamically by changes in enthalpy and/or entropy.
Calculate the ΔG° for a system either from ΔG_f° values, ΔH_f° and ΔS° values, or by applying Hess’ Law.
Predict whether a reaction is thermodynamically favored by evaluation of ΔG°, ΔH°, and ΔS° values for a given chemical or physical process.
Determine the temperature at which a process becomes spontaneous.

One of the challenges of using the second law of thermodynamics to determine if a process is spontaneous is that we must determine the entropy change for the system and the entropy change for the surroundings. An alternative approach involving a new thermodynamic property defined in terms of only system properties was introduced in the late nineteenth century by American mathematician Josiah Willard Gibbs. This new property is called the Gibbs free energy change (ΔG) (or simply the free energy), and it is defined in terms of a system’s enthalpy and entropy as the following derivation shows.

In the previous section, we derived the relationship between ΔS_univ and ΔH_sys:

ΔS_univ = ΔS_sys – $\dfrac{\Delta H_{\text{sys}}}{\text{T}}$

Multiplying both sides of this equation by −T, and rearranging yields the following:

-TΔS_univ = ΔH_sys – TΔS_sys

We can now define a new variable, ΔG_sys, and set it equal to -TΔS_univ.

ΔG_sys = ΔH_sys – TΔS_sys

We often remove the system subscript for simplicity’s sake:

ΔG = ΔH – TΔS

The free energy change is therefore a reliable indicator of the spontaneity of a process, being directly related to ΔS_univ. Table 1 summarizes the relation between the spontaneity of a process and the arithmetic signs of these indicators.

**Table 1.** Relation between Process Spontaneity and Signs of Thermodynamic Properties
ΔS_univ > 0	ΔG < 0	spontaneous
ΔS_univ < 0	ΔG > 0	nonspontaneous
ΔS_univ = 0	ΔG = 0	reversible (at equilibrium)

Calculating Free Energy Change

Free energy is a state function, so its value depends only on the conditions of the initial and final states of the system that have undergone some change. A convenient and common approach to the calculation of free energy changes for physical and chemical reactions is by use of widely available compilations of standard state thermodynamic data. One method involves the use of standard enthalpies and entropies to compute standard free energy changes according to the following relation as demonstrated in Example 1.

ΔG° = ΔH° – TΔS°

Example 1

Evaluation of ΔG° Change from ΔH° and ΔS°
Use standard enthalpy and entropy data from Appendix F to calculate the standard free energy change for the vaporization of water at room temperature (298 K). What does the computed value for ΔG° say about the spontaneity of this process under standard-state conditions?

Solution
The process of interest is the following:

H₂O(ℓ) → H₂O(g)

The standard change in free energy may be calculated using the following equation:

ΔG° = ΔH° – TΔS°

From Appendix F, here is the data:

Substance	ΔH_f° (kJ/mol)	S° (J/mol·K)
H₂O(ℓ)	−285.83	69.91
H₂O(g)	−241.818	188.825

Combining at 298 K:

ΔH° = ΔH_f°(H₂O(g)) – ΔH_f°(H₂O(ℓ)) = (-241.818 $\frac{\text{kJ}}{\text{mol}}$ ) – (-285.83 $\frac{\text{kJ}}{\text{mol}}$ ) = 44.012 $\frac{\text{kJ}}{\text{mol}}$

ΔS° = S°(H₂O(g)) – S°(H₂O(ℓ)) = (188.825 $\frac{\text{J}}{\text{mol}{\cdot}\text{K}}$ ) – (69.91 $\frac{\text{J}}{\text{mol}{\cdot}\text{K}}$ ) = 118.915 $\frac{\text{J}}{\text{mol}{\cdot}\text{K}}$

Converting everything into kJ and combining at 298 K:

ΔG° = ΔH° – TΔS° = 44.012 $\frac{\text{kJ}}{\text{mol}}$ – (298 K × 118.915 $\frac{\text{J}}{\text{mol}{\cdot}\text{K}}$ × $\dfrac{1\ \text{kJ}}{1000\ \text{J}}$ )

ΔG° = 44.012 $\frac{\text{kJ}}{\text{mol}}$ – 35.44 $\frac{\text{kJ}}{\text{mol}}$ = 8.58 $\frac{\text{kJ}}{\text{mol}}$

At 298 K (25 °C) ΔG° > 0, and so boiling is nonspontaneous (not spontaneous) under standard-state conditions.

Check Your Learning
Use standard enthalpy and entropy data from Appendix F to calculate the standard free energy change for the reaction shown here (313 K). What does the computed value for ΔG° say about the spontaneity of this process under standard-state conditions?

C₂H₆(g) → H₂(g) + C₂H₄(g)

Answer:

ΔG° = 99.2 kJ/mol; the reaction is nonspontaneous (not spontaneous) at 313 K under standard-state conditions.

Free energy changes may also use the standard free energy of formation (ΔG_f°), for each of the reactants and products involved in the reaction. The standard free energy of formation is the free energy change that accompanies the formation of one mole of a substance from its elements in their standard states. Similar to the standard enthalpies of formation, ΔG_f° is by definition zero for elemental substances under standard state conditions. The approach to computing the free energy change for a reaction using this approach is the same as that demonstrated previously for enthalpy and entropy changes. For the reaction,

mA + nB → xC + yD

the standard free energy change at room temperature may be calculated as

ΔG° = ∑vΔG_f°(products) – ∑vΔG_f°(reactants) = [xΔG_f°(C) + yΔG_f°(D)] – [mΔG_f°(A) + nΔG_f°(B)]

Example 2

Calculation of ΔG°
Consider the decomposition of red mercury(II) oxide.

HgO(s, red) → Hg(ℓ) + ½ O₂(g)

Calculate the standard free energy change at 298.15 K, ΔG°, using (a) standard free energies of formation and (b) standard enthalpies of formation and standard entropies. Do the results indicate the reaction to be spontaneous or nonspontaneous under standard-state conditions?

Solution
The required data are available in Appendix F and are shown here.

Compound	ΔG_f° (kJ/mol)	ΔH_f° (kJ/mol)	S° (J/mol·K)
HgO (s, red)	−58.54	−90.83	70.29
Hg(ℓ)	0	0	76.02
O₂(g)	0	0	205.14

(a) Using free energies of formation:

ΔG°	=	∑vΔG_f°(products) – ∑vΔG_f°(reactants)
	=	[1 × ΔG_f°(Hg(ℓ)) + ½ × ΔG_f°(O₂(g))] – [1 × ΔG_f°(HgO(s, red))]
	=	[1 × (0 $\frac{\text{kJ}}{\text{mol}}$ ) + ½ × (0 $\frac{\text{kJ}}{\text{mol}}$ )] – [1 × (-58.54 $\frac{\text{kJ}}{\text{mol}}$ )] = 58.54 $\frac{\text{kJ}}{\text{mol}}$

(b) Using enthalpies and entropies of formation:

ΔH°	=	∑vΔH_f°(products) – ∑vΔH_f°(reactants)
	=	[1 × ΔH_f°(Hg(ℓ)) + ½ × ΔH_f°(O₂(g))] – [1 × ΔH_f°(HgO(s, red))]
	=	[1 × (0 $\frac{\text{kJ}}{\text{mol}}$ ) + ½ × (0 $\frac{\text{kJ}}{\text{mol}}$ )] – [1 × (-90.83 $\frac{\text{kJ}}{\text{mol}}$ )] = 90.83 $\frac{\text{kJ}}{\text{mol}}$

ΔS°	=	∑vS°(products) – ∑vS°(reactants)
	=	[1 × S°(Hg(ℓ)) + ½ × S°(O₂(g))] – [1 × S°(HgO(s, red))]
	=	[1 × (76.02 $\frac{\text{J}}{\text{mol}{\cdot}\text{K}}$ ) + ½ × (205.14 $\frac{\text{J}}{\text{mol}{\cdot}\text{K}}$ )] – [1 × (70.29 $\frac{\text{J}}{\text{mol}{\cdot}\text{K}}$ )] = 108.30 $\frac{\text{J}}{\text{mol}{\cdot}\text{K}}$

ΔG° = ΔH° – TΔS° = 90.83 $\frac{\text{kJ}}{\text{mol}}$ – (298.15 K × 108.30 $\frac{\text{J}}{\text{mol}{\cdot}\text{K}}$ × $\dfrac{1\ \text{kJ}}{1000\ \text{J}}$ )

ΔG° = 90.83 $\frac{\text{kJ}}{\text{mol}}$ – 32.29 $\frac{\text{kJ}}{\text{mol}}$ = 58.54 $\frac{\text{kJ}}{\text{mol}}$

Both ways to calculate the standard free energy change at 25 °C give the same numerical value (to four significant figures), and both predict that the process is nonspontaneous (not spontaneous) at room temperature under standard-state conditions.

Check Your Learning
Calculate ΔG° using (a) free energies of formation and (b) enthalpies of formation and entropies (Appendix F). Do the results indicate the reaction to be spontaneous or nonspontaneous at 25 °C under standard-state conditions?

C₂H₄(g) → H₂(g) + C₂H₂(g)

Answer:

141.1 kJ/mol, nonspontaneous

Temperature Dependence of Spontaneity

As was previously demonstrated in this chapter’s section on entropy, the spontaneity of a process may depend upon the temperature of the system. Phase transitions, for example, will proceed spontaneously in one direction or the other depending upon the temperature of the substance. Likewise, some chemical reactions can also exhibit temperature dependent spontaneities. To illustrate this concept, we can look more closely at how the free energy change relates to the enthalpy and entropy change:

ΔG = ΔH – TΔS

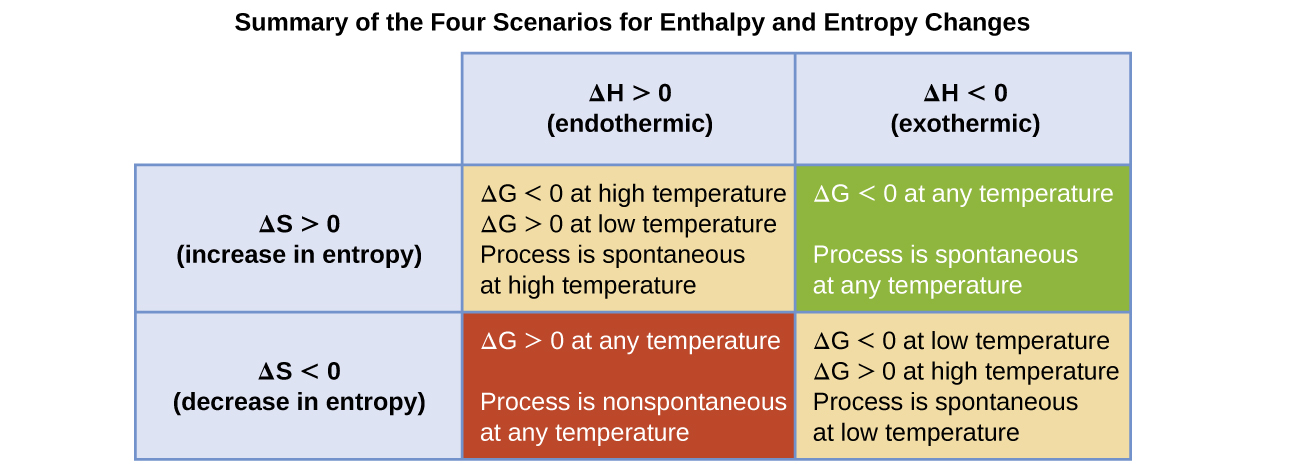
The spontaneity of a process, as reflected in the arithmetic sign of its free energy change, is determined by the signs of the enthalpy and entropy changes and, in some cases, the absolute temperature. Since T is the absolute (kelvin) temperature, it can only have positive values. Four possibilities therefore exist with regard to the signs of the enthalpy and entropy changes:

Both ΔH and ΔS are positive. This condition describes an endothermic process that involves an increase in system entropy. In this case, ΔG will be negative if the magnitude of the TΔS term is greater than ΔH. If the TΔS term is less than ΔH, the free energy change will be positive. Such a process is spontaneous at high temperatures and nonspontaneous at low temperatures.
Both ΔH and ΔS are negative. This condition describes an exothermic process that involves a decrease in system entropy. In this case, ΔG will be negative if the magnitude of the TΔS term is less than ΔH. If the TΔS term’s magnitude is greater than ΔH, the free energy change will be positive. Such a process is spontaneous at low temperatures and nonspontaneous at high temperatures.
ΔH is positive and ΔS is negative. This condition describes an endothermic process that involves a decrease in system entropy. In this case, ΔG will be positive regardless of the temperature. Such a process is nonspontaneous at all temperatures.
ΔH is negative and ΔS is positive. This condition describes an exothermic process that involves an increase in system entropy. In this case, ΔG will be negative regardless of the temperature. Such a process is spontaneous at all temperatures.

These four scenarios are summarized in Table 2.

Table 2: Signs of Enthalpy and Entropy changes and their effect on Gibbs Free Energy.
Sign of ΔH_sys	Sign of ΔS_sys	Sign of ΔG_sys	Product-favored?	Described as…
Negative (Exothermic)	Positive	Always Negative	Yes
Negative (Exothermic)	Negative	Depends on T	Yes at low T	“Enthalpy-driven”
Positive (Endothermic)	Positive	Depends on T	Yes at high T	“Entropy-driven”
Positive (Endothermic)	Negative	Always Positive	No

A table with three columns and four rows is shown. The first column has the phrase, “Delta S greater than zero ( increase in entropy ),” in the third row and the phrase, “Delta S less than zero ( decrease in entropy),” in the fourth row. The second and third columns have the phrase, “Summary of the Four Scenarios for Enthalpy and Entropy Changes,” written above them. The second column has, “delta H greater than zero ( endothermic ),” in the second row, “delta G less than zero at high temperature, delta G greater than zero at low temperature, Process is spontaneous at high temperature,” in the third row, and “delta G greater than zero at any temperature, Process is nonspontaneous at any temperature,” in the fourth row. The third column has, “delta H less than zero ( exothermic ),” in the second row, “delta G less than zero at any temperature, Process is spontaneous at any temperature,” in the third row, and “delta G less than zero at low temperature, delta G greater than zero at high temperature, Process is spontaneous at low temperature.” — **Figure 1.** There are four possibilities regarding the signs of enthalpy and entropy changes.

Example 3

Predicting the Temperature Dependence of Spontaneity
The incomplete combustion of carbon is described by the following equation:

2C(s) + O₂(g) → 2 CO(g)

How does the spontaneity of this process depend upon temperature?

Solution
Combustion processes are exothermic (ΔH < 0). This particular reaction involves an increase in entropy due to the accompanying increase in the amount of gaseous species (net gain of one mole of gas, ΔS > 0). The reaction is therefore spontaneous (ΔG < 0) at all temperatures.

Check Your Learning
Popular chemical hand warmers generate heat by the air-oxidation of iron:

4 Fe(s) + 3 O₂(g) → 2 Fe₂O₃(s)

How does the spontaneity of this process depend upon temperature?

Answer:

ΔH and ΔS are negative; the reaction is spontaneous at low temperatures.

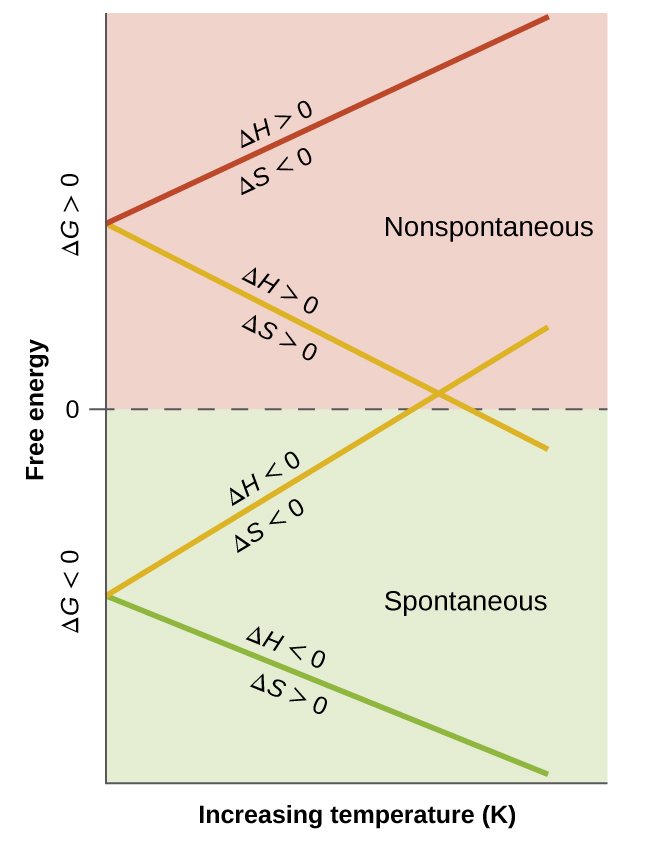
When considering the conclusions drawn regarding the temperature dependence of spontaneity, it is important to keep in mind what the terms “high” and “low” mean. Since these terms are adjectives, the temperatures in question are deemed high or low relative to some reference temperature. A process that is nonspontaneous at one temperature but spontaneous at another will necessarily undergo a change in “spontaneity” (as reflected by its ΔG) as temperature varies. This is clearly illustrated by a graphical presentation of the free energy change equation, in which ΔG is plotted on the y axis versus T on the x axis:

ΔG = (-ΔS)T + ΔH
y = mx + b

Such a plot is shown in Figure 2. A process whose enthalpy and entropy changes are of the same arithmetic sign will exhibit a temperature-dependent spontaneity as depicted by the two yellow lines in the plot. Each line crosses from one spontaneity domain (positive or negative ΔG) to the other at a temperature that is characteristic of the process in question. This temperature is represented by the x-intercept of the line, that is, the value of T for which ΔG is zero:

ΔG = 0 = ΔH – TΔS T₍_{ΔG = 0)} = $\dfrac{\Delta H}{\Delta S}$

And so, saying a process is spontaneous at “high” or “low” temperatures means the temperature is above or below that temperature at which ΔG for the process is zero.

A graph is shown where the y-axis is labeled, “Free energy,” and the x-axis is labeled, “Increasing temperature ( K ).” The value of zero is written midway up the y-axis with the label, “delta G greater than 0,” written above this line and, “delta G less than 0,” written below it. The bottom half of the graph is labeled on the right as, “Spontaneous,” and the top half is labeled on the right as, “Nonspontaneous.” A green line labeled, “delta H less than 0, delta S greater than 0,” extends from a quarter of the way up the y-axis to the bottom right of the graph. A yellow line labeled, “delta H less than 0, delta S less than 0,” extends from a quarter of the way up the y-axis to the middle right of the graph. A second yellow line labeled, “delta H greater than 0, delta S greater than 0,” extends from three quarters of the way up the y-axis to the middle right of the graph. A red line labeled, “delta H greater than 0, delta S less than 0,” extends from three quarters of the way up the y-axis to the top right of the graph. — **Figure 2.** These plots show the variation in ΔG with temperature for the four possible combinations of arithmetic sign for ΔH and ΔS.

Example 4

Equilibrium Temperature for a Phase Transition
As defined in the chapter on liquids and solids, the boiling point of a liquid is the temperature at which its gas and liquid phases are in equilibrium (that is, when vaporization and condensation occur at equal rates). Use the information in Appendix F to estimate the boiling point of water.

Solution
The process of interest is the following phase change:

H₂O(ℓ) → H₂O(g)

When this process is at equilibrium, ΔG = 0, so the following is true:

0 = ΔH° – TΔS° T₍_{ΔG = 0)} = $\dfrac{\Delta H}{\Delta S}$

Using the standard thermodynamic data from Appendix F,

ΔH° = ΔH_f°(H₂O(g)) – ΔH_f°(H₂O(ℓ)) = (-241.818 $\frac{\text{kJ}}{\text{mol}}$ ) – (-285.83 $\frac{\text{kJ}}{\text{mol}}$ ) = 44.012 $\frac{\text{kJ}}{\text{mol}}$

ΔS° = S°(H₂O(g)) – S°(H₂O(ℓ)) = 188.825 $\frac{\text{J}}{\text{mol}{\cdot}\text{K}}$ – 69.91 $\frac{\text{J}}{\text{mol}{\cdot}\text{K}}$ = 118.915 $\frac{\text{J}}{\text{mol}{\cdot}\text{K}}$

T = $\dfrac{\Delta H}{\Delta S} = \dfrac{44.012 \times 10^{3} \frac{\text{J}}{\text{mol}}}{118.915 \frac{\text{J}}{\text{mol}{\cdot}\text{K}}}$ = 370.1 K = 97.0 °C

The accepted value for water’s normal boiling point is 373.2 K (100.0 °C), and so this calculation is in reasonable agreement. Note that the values for enthalpy and entropy changes data used were derived from standard data at 298 K (Appendix F). If desired, you could obtain more accurate results by using enthalpy and entropy changes determined at (or at least closer to) the actual boiling point.

Check Your Learning
Use the information in Appendix F to estimate the boiling point of CS₂.

Answer:

319.8 K (accepted value 319 K)

Key Concepts and Summary

So far, many of the thermodynamic properties we have learned about have been in terms of the system, surroundings, or universe. By making a few approximations, Gibbs Free Energy is dependent on the enthalpy and entropy of the system, with no dependence on the surroundings or universe. The spontaneity of a process can still depend on the temperature of the system, depending on the sign of the enthalpy or entropy. If the enthalpy and entropy have opposite signs, the process is not temperature dependent and is either always spontaneous or nonspontaneous at all temperatures. If the enthalpy and entropy have the same sign, the process is temperature dependent and will only be spontaneous at either high or low temperatures. The temperature at which the process crosses over from nonspontaneous to spontaneous can be calculated by setting the Gibbs Free Energy to zero (0 = ΔH – TΔS).

Key Equations

ΔG° = ΔH° – TΔS°
ΔG° = ∑vΔG_f°(products) – ∑vΔG_f°(reactants)

Glossary

Gibbs Free Energy: free energy, defined in terms of a system’s enthalpy and entropy, used to determine if a process is spontaneous

standard free energy of formation (ΔG_fº): the free energy change that accompanies the formation of one mole of a substance from its elements in their standard states

Chemistry End of Section Exercises

Explain how to interpret the sign of ΔG in terms of spontaneous and nonspontaneous.
From the values of ΔH° and ΔS°, indicate whether a process would be spontaneous, nonspontaneous, or if more information is necessary.
1. ΔH° = 25.3 kJ/mol, ΔS° = 300.1 J/mol·K
2. ΔH° = – 25.3 kJ/mol, ΔS° = 300.1 J/mol·K
3. ΔH° = 25.3 kJ/mol, ΔS° = -300.1 J/mol·K
4. ΔH° = -25.3 kJ/mol, ΔS° = -300.1 J/mol·K
A reaction has ΔH_rxn° = 100 kJ/mol and a ΔS_rxn° = 250 J/mol·K. Is the reaction spontaneous at room temperature? If not, under what temperature conditions will it become spontaneous?
Use the following table to find the ΔG° for the combustion of ethanol at 298 K:

Substance ΔH_f° (kJ/mol) S° (J/mol·K)

C₂H₅OH(ℓ) –277.6 160.7

CO₂(g) –393.51 213.7

H₂O(ℓ) –285.83 69.91

O₂(g) 0 205.2
What can you say about the temperature dependence, in regards to spontaneity, for the reaction in problem 4?
What is the value of ΔG° at 373 K for the oxidation of solid elemental sulfur to gaseous sulfur dioxide, as shown below?
S(s, rhombic) + O₂(g) ⇌ SO₂(g)

At 298 K, ΔH° for this reaction is -269.9 kJ/mol, and ΔS° is +11.6 J/K mol.
Use the standard free energy of formation data in Appendix F to determine the free energy change for each of the following reactions, which are run under standard state conditions and 25 °C. Identify each as either spontaneous or nonspontaneous at these conditions.
1. MnO₂(s) → Mn(s) + O₂(g)
2. H₂(g) + Br₂(ℓ) → 2 HBr(g)
3. 2 LiOH(s) + CO₂(g) → Li₂CO₃(s) + 2 H₂O(g)
4. CH₄(g) + 3 Cl₂(g) → C(s;graphite) + 2 H₂O(g)
5. CS₂(g) + 3 Cl₂(g) → CCl₄(g) + S₂Cl₂(g)
Tungsten has a melting point of 3422 °C and a heat of fusion of 35.3 kJ/mol. What is ΔS°_fus for tungsten?
Determine the boiling point of ethanol, in °C, from the following information:
Ethanol(ℓ) ⇌ Ethanol(g) ΔH = 38.56 kJ/mol ΔS = 109.67 J/mol·K
Sodium carbonate can be made by heating sodium bicarbonate, according to the reaction:
2 NaHCO₃(s) → Na₂CO₃(s) + CO₂(g) + H₂O(g)

Given that ΔH° = 128.9 kJ/mol and ΔG° = 33.1 kJ/mol at 25 °C, above what minimum temperature will the reaction become spontaneous under standard state conditions?
When two white crystalline substances are mixed in a beaker, the beaker spontaneously cools to the point of being able to freeze to a wet wooden board. The reaction is as follows:
Ba(OH)₂(s) + 2 NH₄SCN(s) → Ba(SCN)₂(aq) + 2 NH₃(g) + 2 H₂O(ℓ)

Which of the following statements must be true about the process? Justify your answer in a few sentences.
1. The reaction would cease to be spontaneous at sufficiently high temperatures.
2. The process is entropy-driven.
3. The process is exothermic.
4. The entropy change is negative.
5. The process is enthalpy-driven.
A reaction that is not spontaneous at low temperature can become spontaneous at high temperature if ∆H is _____ and ∆S is _____.
1. positive, positive
2. negative, negative
3. positive, negative
4. negative, positive
5. None of the above. If a reaction is nonspontaneous at low temperatures, it will be nonspontaneous at all temperatures.
Given the following table of thermodynamic data, complete the following sentence. The vaporization of PCl₃(ℓ) is _____.

Substance ΔH°_f (kJ/mol) S° (J/K·mol)

PCl₃ (g) -288.07 311.7

PCl₃ (ℓ) -319.6 217
1. nonspontaneous at low temperature and spontaneous at high temperature.
2. spontaneous at low temperature and nonspontaneous at high temperature.
3. spontaneous at all temperatures.
4. nonspontaneous at all temperatures.
5. not enough information is given to draw a conclusion.
When barium chloride and sodium sulfate solutions are mixed, a white solid precipitate of barium sulfate forms immediately. Which of the following is correct for this reaction?
1. ΔH < 0, ΔS < 0, ΔG < 0
2. ΔH > 0, ΔS > 0, ΔG < 0
3. ΔH < 0, ΔS > 0, ΔG < 0
4. ΔH > 0, ΔS > 0, ΔG > 0
5. ΔH > 0, ΔS < 0, ΔG > 0
For the reaction: H₂(g) + S(s) → H₂S(g), ΔH° = -20.2 kJ/mol and ΔS° = +43.1 J/mol∙K. Which of these statements is correct?
1. The reaction is only spontaneous at low temperatures
2. The reaction is spontaneous at all temperatures
3. ΔG° becomes less favorable as temperature increases
4. The reaction is only spontaneous at high temperatures
5. The reaction is at equilibrium at 25 °C under standard conditions
Liquid ammonia, NH₃(ℓ) has a boiling point of -33°C. What are the signs of ΔH, ΔS, and ΔG for the evaporation of liquid ammonia at -60°C?

Answers to Chemistry End of Section Exercises

A process with a negative free energy (ΔG) will be spontaneous. A process with a positive free energy will be nonspontaneous. A process with a zero free energy is at equilibrium, or is said to be reversible.
(a) Cannot be determined with just the information provided. With a positive enthalpy and a positive entropy, temperature must also be known to determine spontaneity.
(b) Spontaneous. A process with a negative enthalpy and a positive entropy will always be spontaneous.
(c) Nonspontaneous. A process with a positive enthalpy and a negative entropy will always be nonspontaneous.
(d) Cannot be determined with just the information provided. With a negative enthalpy and a negative entropy, temperature must also be known to determine spontaneity.
The reaction is nonspontaneous at room temperature. Above 400 K, ΔG will become negative, and the reaction will become spontaneous.
ΔG° = -1325.4 kJ/mol
Both ΔH and ΔS are negative. the reaction at 298 K is spontaneous, however, as the temperature is increased, eventually the reaction would become nonspontaneous. (However, this would occur at 9822 K and there would no longer be any liquid ethanol to combust at the temperature!)
-274.2 kJ/mol
(a) 465.1 kJ/mol; Nonspontaneous;
(b) -106.9 kJ/mol; Spontaneous
(c) -317.08 kJ/mol; Spontaneous
(d) -406.4 kJ/mol; Spontaneous
(e) -159.51 kJ/mol; Spontaneous
9.55 J/mol·K
78.5 °C
401 K
B. For a spontaneous process, when both ΔH and ΔS are positive, the value of ΔG is only negative when TΔS is greater in magnitude than ΔH. This reaction is, therefore, entropy driven.
A
A
A
B
ΔH > 0, ΔS > 0, ΔG > 0

Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 103/104 Resource Book Copyright © by Chem 103 Textbook Team and Chem 104 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Substance	ΔH°_f (kJ/mol)	S° (J/K·mol)
PCl₃ (g)	-288.07	311.7
PCl₃ (ℓ)	-319.6	217

Substance	ΔH_f° (kJ/mol)	S° (J/mol·K)
C₂H₅OH(ℓ)	–277.6	160.7
CO₂(g)	–393.51	213.7
H₂O(ℓ)	–285.83	69.91
O₂(g)	0	205.2