M4Q2: Stoichiometry

Introduction

The section explores stoichiometry of chemical reactions. We will examine how we can use a chemical reaction to relate the mass and moles of reactants and products. This section includes worked examples, sample problems, and a glossary.

Learning Objectives for Stoichiometry

  • Use balanced equations to calculate quantities of reactants and/or products from appropriate data.
    | Stoichiometry |

| Key Concepts and Summary | Glossary | End of Section Exercises |

Stoichiometry

A balanced chemical equation provides a great deal of information in a very succinct format. Chemical formulas provide the identities of the reactants and products involved in the chemical change, allowing classification of the reaction. Coefficients provide the relative numbers of these chemical species, allowing a quantitative assessment of the relationships between the amounts of substances consumed and produced by the reaction. These quantitative relationships are known as the reaction’s stoichiometry, a term derived from the Greek words stoicheion (meaning “element”) and metron (meaning “measure”). In this section, the use of balanced chemical equations for various stoichiometric applications is explored.

The general approach to using stoichiometric relationships is similar in concept to the way people go about many common activities. Food preparation, for example, offers an appropriate comparison. A recipe for making eight pancakes calls for 1 cup pancake mix, ¾ cup milk, and one egg. The “equation” representing the preparation of pancakes per this recipe is

1 cup mix + ¾ cup milk + 1 egg  →  8 pancakes

If two dozen pancakes are needed for a big family breakfast, the ingredient amounts must be increased proportionally according to the amounts given in the recipe. For example, the number of eggs required to make 24 pancakes is

24 pancakes × \dfrac{1 \;\text{egg}}{8 \;\rule[0.5ex]{4em}{0.1ex}\hspace{-4em}\text{pancakes}} = 3 eggs

Balanced chemical equations are used in much the same fashion to determine the amount of one reactant required to react with a given amount of another reactant, or to yield a given amount of product, and so forth. The coefficients in the balanced equation are used to derive stoichiometric factors that permit computation of the desired quantity. To illustrate this idea, consider the production of ammonia by reaction of hydrogen and nitrogen:

N2(g) + 3 H2(g)  →  2 NH3(g)

This equation shows ammonia molecules are produced from hydrogen molecules in a 2:3 ratio, and stoichiometric factors may be derived using any amount (number) unit:

\dfrac{2 \;\text{NH}_3 \;\text{molecules}}{3 \;\text{H}_2 \;\text{molecules}} or \dfrac{2 \;\text{dozen NH}_3 \;\text{molecules}}{3 \;\text{dozen H}_2 \;\text{molecules}} or \dfrac{2 \;\text{mol NH}_3 \;\text{molecules}}{3 \;\text{mol H}_2 \;\text{molecules}}

These stoichiometric factors can be used to compute the number of ammonia molecules produced from a given number of hydrogen molecules, or the number of hydrogen molecules required to produce a given number of ammonia molecules. Similar factors may be derived for any pair of substances in any chemical equation.

Example 1

Moles of Reactant Required in a Reaction
How many moles of I2 are required to react with 0.429 mol of Al according to the following equation (see Figure 1)?

2 Al(s) + 3 I2(s)  ⟶  2 AlI3(s)

This figure shows three photos with an arrow leading from one to the next. The first photo shows a small pile of iodine and aluminum on a white surface. The second photo shows a small amount of purple smoke coming from the pile. The third photo shows a large amount of purple and gray smoke coming from the pile.
Figure 1. Aluminum and iodine react to produce aluminum iodide. The heat of the reaction vaporizes some of the solid iodine as a purple vapor. (credit: modification of work by Mark Ott)

Solution
Referring to the balanced chemical equation, the stoichiometric factor relating the two substances of interest is \dfrac{3 \;\text{mol I}_2}{2 \;\text{mol Al}}. The molar amount of iodine is derived by multiplying the provided molar amount of aluminum by this factor:

This figure shows two pink rectangles. The first is labeled, “Moles of A l.” This rectangle is followed by an arrow pointing right to a second rectangle labeled, “Moles of I subscript 2.”

mol I2 = 0.429 mol Al × \dfrac{3\;\text{mol}\;\text{I}_2}{2\;\rule[0.5ex]{3em}{0.1ex}\hspace{-3em} \text{mol Al}} = 0.644 mol I2


Check Your Learning
How many moles of Ca(OH)2 are required to react with 1.36 mol of H3PO4 to produce Ca3(PO4)2 according to the following equation?

3 Ca(OH)2(aq) + 2 H3PO4(aq)  →  Ca3(PO4)2(s) + 6 H2O(ℓ)

Answer:

2.04 mol

Example 2

Number of Product Molecules Generated by a Reaction
How many carbon dioxide molecules are produced when 0.75 mol of propane is combusted according to this equation?

C3H8(g) + 5 O2(g)  →  3 CO2(g) + 4 H2O(ℓ)

Solution
The approach here is the same as for Example 1, though the absolute number of molecules is requested, not the number of moles of molecules. This will simply require use of the moles-to-numbers conversion factor, Avogadro’s number.

The balanced equation shows that carbon dioxide is produced from propane in a 3:1 ratio:

\dfrac{3 \;\text{mol CO}_2}{1 \;\text{mol C}_3 \text{H}_8}

Using this stoichiometric factor, the provided molar amount of propane, and Avogadro’s number,

This figure shows two pink rectangles. The first is labeled, “Moles of C subscript 3 H subscript 8.” This rectangle is followed by an arrow pointing right to a second rectangle labeled, “Moles of C O subscript 2.”

0.75 \;\rule[0.5ex]{4.5em}{0.1ex}\hspace{-4.5em}\text{mol C}_3 \text{H}_8} \times \dfrac{3 \;\rule[0.5ex]{4em}{0.1ex}\hspace{-4em} \text{mol CO}_2}{1 \;\rule[0.5ex]{4.5em}{0.1ex}\hspace{-4.5em}\text{mol C}_3 \text{H}_8} \times \dfrac{6.022 \times 10^{23} \;\text{CO}_2 \;\text{molecules}}{\rule[0.5ex]{4em}{0.1ex}\hspace{-4em} \text{mol CO}_2} = 1.4 × 1024 CO2 molecules

Check Your Learning
How many NH3 molecules are produced by the reaction of 4.0 mol of Ca(OH)2 according to the following equation:

(NH4)2SO4(aq) + Ca(OH)2(aq)  →  2 NH3(g) + CaSO4(s) + 2 H2O(ℓ)

Answer:

4.8 × 1024 NH3 molecules

These examples illustrate the ease with which the amounts of substances involved in a chemical reaction of known stoichiometry may be related. Directly measuring numbers of atoms and molecules is, however, not an easy task, and the practical application of stoichiometry requires that we use the more readily measured property of mass.

Example 3

Relating Masses of Reactants and Products
What mass of sodium hydroxide, NaOH, would be required to produce 16 g of the antacid milk of magnesia [magnesium hydroxide, Mg(OH)2] by the following reaction?

MgCl2(aq) + 2 NaOH(aq)  →  Mg(OH)2(s) + NaCl(aq)

Solution
The approach used previously in Example 1 and Example 2 is likewise used here; that is, we must derive an appropriate stoichiometric factor from the balanced chemical equation and use it to relate the amounts of the two substances of interest. In this case, however, masses (not molar amounts) are provided and requested, so additional steps of the sort learned in the previous chapter are required. The calculations required are outlined in this flowchart:

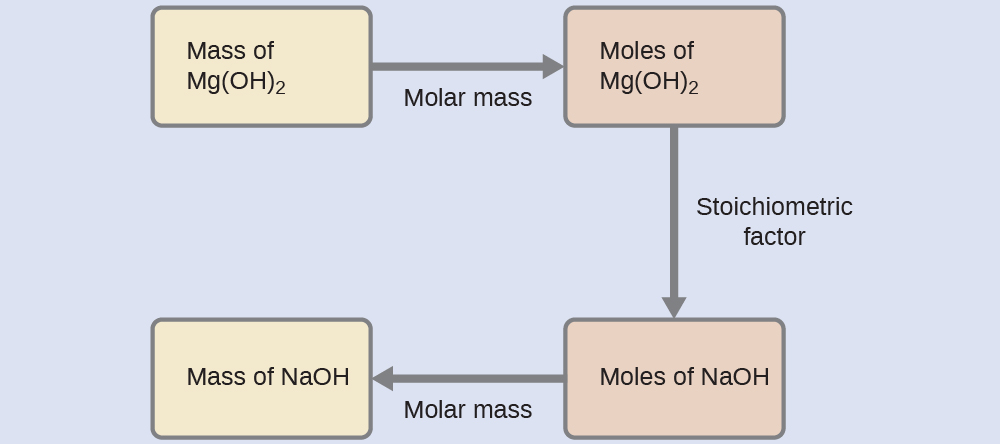
This figure shows four rectangles. The first is shaded yellow and is labeled, “Mass of M g ( O H ) subscript 2.” This rectangle is followed by an arrow pointing right to a second rectangle which is shaded pink and is labeled, “Moles of M g ( O H ) subscript 2.” This rectangle is followed by an arrow pointing right to a third rectangle which is shaded pink and is labeled, “Moles of N a O H.” This rectangle is followed by an arrow pointing right to a fourth rectangle which is shaded yellow and is labeled, “Mass of N a O H.”

16 \;\rule[0.5ex]{5em}{0.1ex}\hspace{-5em}\text{g Mg(OH)}_2 \times \dfrac{1 \;\rule[0.5ex]{6em}{0.1ex}\hspace{-6em}\text{mol Mg(OH)}_2}{58.3 \;\rule[0.5ex]{5em}{0.1ex}\hspace{-5em}\text{g Mg(OH)}_2} \times \dfrac{2 \;\rule[0.5ex]{4.75em}{0.1ex}\hspace{-4.75em}\text{mol NaOH}}{1 \;\rule[0.5ex]{6em}{0.1ex}\hspace{-6em}\text{mol Mg(OH)}_2} \times \dfrac{40.0 \;\text{g NaOH}}{1 \;\rule[0.5ex]{4.75em}{0.1ex}\hspace{-4.75em}\text{mol NaOH}} = 22 g NaOH

Check Your Learning
What mass of gallium oxide, Ga2O3, can be prepared from 29.0 g of gallium metal? The equation for the reaction is:

4 Ga(s) + 3 O2(g)  →  2 Ga2O3(s)

Answer:

39.0 g

Example 4

Relating Masses of Reactants
What mass of oxygen gas, O2, from the air is consumed in the combustion of 702 g of octane, C8H18, one of the principal components of gasoline?

2 C8H18(ℓ) + 25 O2(g)  →  16 CO2(g) + 18 H2O(ℓ)

Solution
The approach required here is the same as for the Example 3, differing only in that the provided and requested masses are both for reactant species.

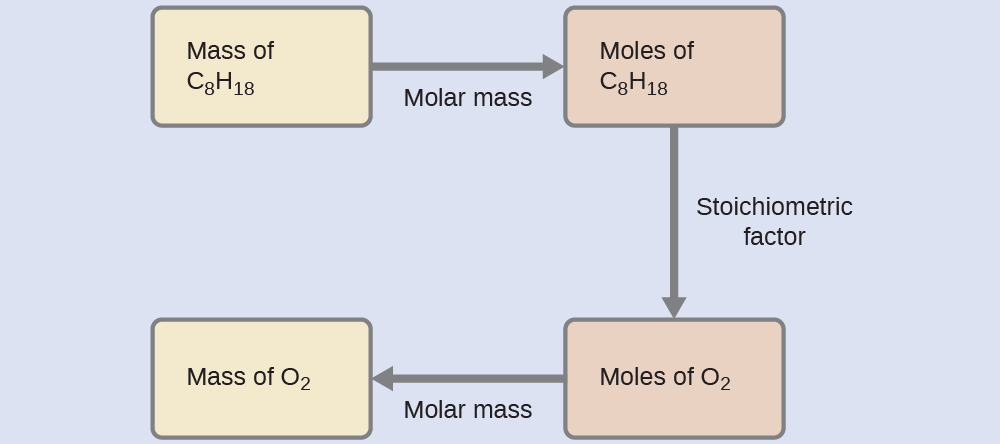
This figure shows four rectangles. The first is shaded yellow and is labeled, “Mass of C subscript 8 H subscript 18.” This rectangle is followed by an arrow pointing right to a second rectangle which is shaded pink and is labeled, “Moles of C subscript 8 H subscript 18.” This rectangle is followed by an arrow pointing right to a third rectangle which is shaded pink and is labeled, “Moles of O subscript 2.” This rectangle is followed by an arrow pointing right to a fourth rectangle which is shaded yellow and is labeled, “Mass of O subscript 2.”

702\;\rule[0.5ex]{3.5em}{0.1ex}\hspace{-3.5em}\text{g C}_8 \text{H}_{18}} \times \dfrac{1 \;\rule[0.5ex]{4.5em}{0.1ex}\hspace{-4.5em}\text{mol C}_8 \text{H}_{18}}{114.23 \;\rule[0.5ex]{3.5em}{0.1ex}\hspace{-3.5em}\text{g C}_8 \text{H}_{18}} \times \dfrac{25 \;\rule[0.5ex]{3.25em}{0.1ex}\hspace{-3.25em}\text{mol O}_2}{2 \;\rule[0.5ex]{4.5em}{0.1ex}\hspace{-4.5em}\text{mol C}_8 \text{H}_{18}} \times \dfrac{32.00 \;\text{g O}_2}{\rule[0.5ex]{3.25em}{0.1ex}\hspace{-3.25em}\text{mol O}_2} = 2.46 × 103 g O2

Check Your Learning
What mass of CO is required to react with 25.13 g of Fe2O3 according to the equation:

Fe2O3(s) + 3 CO(g)  →  2 Fe(s) + 3 CO2(g)

Answer:

13.22 g

Key Concepts and Summary

A balanced chemical equation may be used to describe a reaction’s stoichiometry (the relationships between amounts of reactants and products). Coefficients from the equation are used to derive stoichiometric factors that subsequently may be used for computations relating reactant and product masses, molar amounts, and other quantitative properties.

Glossary

stoichiometric factor
ratio of coefficients in a balanced chemical equation, used in computations relating amounts of reactants and products
stoichiometry
relationships between the amounts of reactants and products of a chemical reaction

Chemistry End of Section Exercises

  1. Write the balanced equation, then outline the steps necessary to determine the information requested in each of the following:
    1. The number of moles and the mass of chlorine, Cl2, required to react with 10.0 g of sodium metal, Na, to produce sodium chloride, NaCl.
    2. The number of moles and the mass of oxygen, O2, formed by the decomposition of 1.252 g of mercury(II) oxide.
    3. The number of moles and the mass of sodium nitrate, NaNO3, required to produce 128 g of oxygen. (NaNO2 is the other product)
    4. The number of moles and the mass of carbon dioxide formed by the combustion of 20.0 kg of carbon in an excess of oxygen.
    5. The number of moles and the mass of copper(II) carbonate needed to produce 1.500 kg of copper(II) oxide. (CO2 is the other product.)
    6. This figure includes two structural formulas. It reads, “The number of moles and the mass of,” which is followed by a structure with two C atoms bonded with a single horizontal at the center. Both C atoms have H atoms bonded above and below. The C atom to the left has a B r atom bonded to its left. The C atom to the right has a B r atom bonded to its right. Following this structure, the figure reads, “formed by the reaction of 12.85 g of,” which is followed by a structure with two C atoms connected with a horizontal double bond. The C atom to the left has H atoms bonded above and to the left and below and to the left. The C atom to the right has H atoms bonded above and to the right and below and to the right. The figure ends with, “with an excess of B r subscript 2.”
  2. Determine the number of moles and the mass requested for each reaction in Chemistry End of Section Exercise 1.
  3. Silver is often extracted from ores such as K[Ag(CN)2] and then recovered by the reaction:
    2 K[Ag(CN)2](aq) + Zn(s)  →  2 Ag(s) + Zn(CN)2(aq) + 2 KCN(aq)
    1. How many molecules of Zn(CN)2 are produced by the reaction of 35.27 g of K[Ag(CN)2]?
    2. What mass of Zn(CN)2 is produced?
  4. Carborundum is silicon carbide, SiC, a very hard material used as an abrasive on sandpaper and in other applications. It is prepared by the reaction of pure sand, SiO2, with carbon at high temperature. Carbon monoxide, CO, is the other product of this reaction. Write the balanced equation for the reaction, and calculate how much SiO2 is required to produce 3.00 kg of SiC.
  5. Automotive air bags inflate when a sample of sodium azide, NaN3, is very rapidly decomposed:
    2 NaN3(s)  →  2 Na(s) + 3 N2(g)

    What mass of sodium azide is required to produce 73.6 L of nitrogen gas with a density of 1.25 g/L?

  6. Urea, CO(NH2)2, is manufactured on a large scale for use in producing urea-formaldehyde plastics and as a fertilizer. What is the maximum mass of urea that can be manufactured from the CO2 produced by combustion of 1.00×103 kg of carbon followed by the reaction?
    CO2(g) + 2 NH3(g)  →  CO(NH2)2(s) + H2O(ℓ)
  7. In an accident, a solution containing 2.5 kg of nitric acid was spilled. Two kilograms of Na2CO3 was quickly spread on the area and CO2 was released by the reaction. Was sufficient Na2CO3 used to neutralize all of the acid?
  8. A compact car gets 37.5 miles per gallon on the highway. If gasoline contains 84.2% carbon by mass and has a density of 0.8205 g/mL, determine the mass of carbon dioxide produced during a 500-mile trip (3.785 liters per gallon).
  9. A mordant is a substance that combines with a dye to produce a stable fixed color in a dyed fabric. Calcium acetate is used as a mordant. It is prepared by the reaction of acetic acid with calcium hydroxide.
    2 CH3CO2H(ℓ) + Ca(OH)2(aq)  →  Ca(CH3CO2)2(aq) + 2 H2O(ℓ)

    What mass of Ca(OH)2 is required to react with the acetic acid in 25.0 mL of a solution having a density of 1.065 g/mL and containing 58.0% acetic acid by mass?

  10. You have a solid that is either copper(I) oxide or copper(II) oxide. You burn 5.000 g of the unknown solid in the presence of H2(g) to generate solid copper and 1.133 g H2O(g).
    1. Write the balanced chemical equation assuming the compound is copper(I) oxide.
    2. Write the balanced chemical equation assuming the compound is copper(II) oxide.
    3. Use stoichiometry to identify the unknown compound.
  11. Upon heating, solid CaCO3 decomposes into solid CaO and CO2 gas.
    1. Write the balanced chemical equation, including states.
    2. A 1.500 g mixture of solid CaCO3 and solid CaO is heated in an open container.  After the decomposition reaction from part (a) is complete, the mass of the solid product is 1.103 g.  Determine the mass percentage of CaCO3 in the original mixture.

Answers to Chemistry End of Section Exercises

  1. (a) Cl2(g) + 2 Na(s)  →  2 NaCl(s). First, convert the 10.0g Na to moles Na via molar mass, then the molar ratio of Na to Cl2 to get moles Cl2 (1 mol Cl2/2 mol Na). To get mass of Cl2, take the moles of Cl2 then multiply by molar mass
    (b) 2 HgO(s)  →  2 Hg(ℓ) + O2(g). First, convert 1.252g of HgO to moles of HgO with the molar mass of HgO. Then with the molar ratio of O2 to HgO, convert moles of HgO to mol O2 (1 mol O2/2 mol HgO) to get the amount of moles of O2. To get grams of O2, take the moles of O2 and multiply by the molar mass of O2;
    (c) 2 NaNO3(s)  →  O2(g) + 2 NaNO2(s). First, convert the mass of O2 to moles of O2, then use the molar ratio of O2 and NaNO3 to get moles of NaNO3 (2 mol NaNO3/1 mol O2). To get the mass of NaNO3, take the moles of NaNO3 and convert to grams NaNO3 by multiplying moles by the molar mass of NaNO3
    (d) C(s) + O2(g)  →  CO2(g). First, convert kg C to g C. Then, convert g C to moles C, then moles C to moles CO2 using the molar ratio, which is 1:1. To get the mass of CO2, multiply the mol CO2 by the molar mass
    (e) CuCO3(s)  →  CuO(s) + CO2(g). First convert kg to g, then convert g CuO to moles CuO using molar mass, then use the molar ratio (1:1) to get to moles of CuCO3. Using moles of CuCO3, convert to grams by multiplying it by the molar mass of CuCO3
    (f) ethelyene + Br2  →  1,2-dibromoethane. Convert 12.85g ethylene to moles using molar mass of ethylene, then use the molar ratio of ethylene to 1,2-dibromoethane (1:1) to calculate moles of 1,2-dibromoethane. To calculate grams of 1,2-dibromoethane, multiple the moles of it by its molar mass.
  2. (a) 0.217 mol Cl2, 15.4 g Cl2
    (b) 2.890 × 10−3 mol O2, 9.248 × 10−2 g O2
    (c) 8.00 mol NaNO3, 6.8 × 102 g NaNO3
    (d) 1665 mol CO2, 73.3 kg CO2
    (e) 18.86 mol CuO, 2.330 kg CuCO3
    (f) 0.4580 mol C2H4Br2, 86.05 g C2H4Br2
  3. (a) 5.337 × 1022 molecules; (b) 10.41 g Zn(CN)2
  4. SiO2(s) + 3 C(s)  →  SiC(s) + 2 CO(g).  4.50 kg SiO2
  5. 142 g NaN3
  6. 5.00 × 103 kg
  7. No, there was not sufficient sodium carbonate to neutralize all of the acid
  8. 128 kg
  9. 9.53 g Ca(OH)2
  10. (a) Cu2O(s) + H2(g)  →  2 Cu(s) + H2O(g)
    (b) CuO(s) + H2(g)  →  Cu(s) + H2O(g)
    (c) The unknown is CuO
  11. (a) CaCO3(s)  →  CaO(s) + CO2(g)
    (b) 60.2%
Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 103/104 Resource Book Copyright © by Chem 103 Textbook Team and Chem 104 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.