M16Q4: Titration of a Strong Acid with a Strong Base

Chem 103 Textbook Team; Chem 104 Textbook Team

M16Q4: Titration of a Strong Acid with a Strong Base

Learning Objectives

Describe the equipment and chemical reactions involved in acid-base titrations.
Determine pH and concentrations of chemical species at any point in the titration of a strong acid by a strong base or a strong base by a strong acid.
Select an appropriate indicator for a given acid-base titration.
| Acid-Base Indicators |

| Key Concepts and Summary | Glossary | End of Section Exercises |

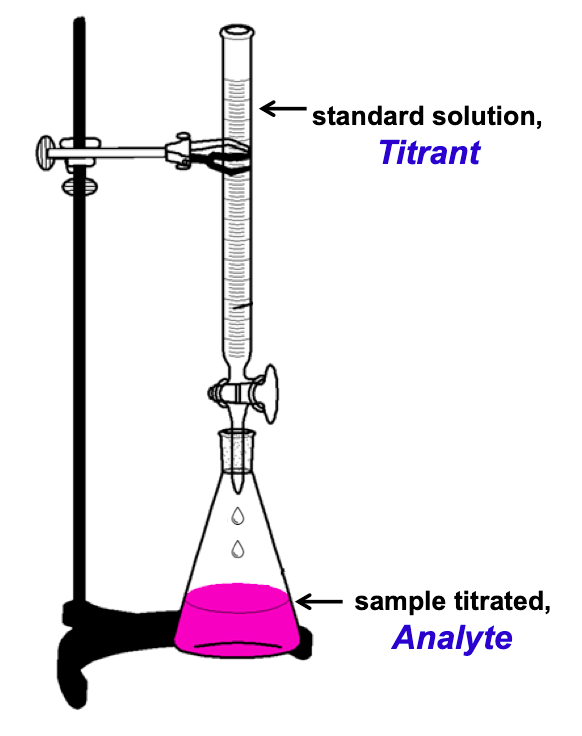
A typical titration analysis involves the use of a buret (Figure 1) to make incremental additions of a solution containing a known concentration of some substance (the titrant) to a sample solution containing the substance whose concentration is to be measured (the analyte). The titrant and analyte undergo a chemical reaction of known stoichiometry, and so the volume of titrant solution required for complete reaction with the analyte (the equivalence point of the titration) can be used to determine the analyte concentration. Though any type of chemical reaction may serve as the basis for a titration analysis, the most common involve precipitation, acid-base, or redox reactions..

**Figure 1:** Buret titrating standard solution (titrant) into unknown solution (analyte).

Titration Curve

Previously, when we studied acid-base reactions in solution, we focused only on the point at which the acid and base were stoichiometrically equal. No consideration was given to the pH of the solution before, during, or after the neutralization. Example 1 looks at several stages of an acid-base reaction, including after neutralization.

Example 1

Calculating pH for Titration Solutions: Strong Acid/Strong Base
A titration is carried out for 25.00 mL of 0.100 M HCl (strong acid) with 0.100 M of a strong base NaOH the titration curve is shown in Figure 2. Calculate the pH at these volumes of added base solution:

0.00 mL
12.50 mL
25.00 mL
37.50 mL

Solution
Since HCl is a strong acid, we can assume that all of it dissociates. The initial concentration of H₃O⁺ is 0.100 M. When the base solution is added, it also dissociates completely, providing OH⁻ ions. The H₃O⁺ and OH⁻ ions neutralize each other, so only those of the two that were in excess remain, and their concentration determines the pH. Thus, the solution is initially acidic (pH < 7), but eventually all the hydronium ions present from the original acid are neutralized, and the solution becomes neutral. As more base is added, the solution turns basic.

First, we write out our reaction, reacting the strong base with HCl:

OH^–(aq) + H₃O⁺(aq) → 2 H₂O(ℓ)

Second, we create an SCF (Start→Change→Finish) table, finding the moles of acid to begin with:

25.00 mL × $\dfrac{1\ \text{L}}{1000\ \text{mL}} \times \dfrac{0.100\ \text{mol H}_{3}\text{O}^{+}}{1\ \text{L}}$ = 0.00250 moles H₃O⁺

OH^–(aq) + H₃O⁺(aq) → 2 H₂O(ℓ)

S (Start)

0.00250

–

C (Change)

F (Finish)

Now we are set up to approach the problem!

(a) added base = 0 mL

Since we have not added any base to the solution yet, we can first just calculate the pH of the initial HCl solution.

pH = -log[H₃O⁺] = -log(0.100 M) = 1.000

(b) added base = 12.50 mL

Once we start to add base, we will calculate the moles of base added and put that value in our SCF table.

12.50 mL × $\dfrac{1\ \text{L}}{1000\ \text{mL}} \times \dfrac{0.100\ \text{mol NaOH}}{1\ \text{L}} \times \dfrac{1\ \text{mol OH}^{-}}{1\ \text{mol NaOH}}$ = 0.00125 moles OH^–

OH^–(aq) + H₃O⁺(aq) → 2 H₂O(ℓ)

S (Start)

0.00125

0.00250

–

C (Change)

F (Finish)

Then, we subtract whichever number of moles is smaller between the two reactants, ensuring that at least one reactant’s quantity goes to zero and other reactant’s remaining quantity is positive.

	OH^–(aq) + H₃O⁺(aq) → 2 H₂O(ℓ)
S (Start)	0.00125	0.00250	–
C (Change)	-0.00125	-0.00125	–
F (Finish)	0	0.00125	–

Lastly, we ask ourselves “What’s in my beaker?”. In this case, we have excess strong acid and need to calculate the new concentration of the hydronium ion in order to calculate the resulting pH.

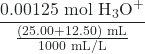$\dfrac{0.00125\ \text{mol H}_{3}\text{O}^{+}}{\frac{(25.00 + 12.50)\ \text{mL}}{1000\ \text{mL/L}}}$ = 0.0333 M H₃O⁺

pH = -log[H₃O⁺] = 1.477

(c) added base = 25.00 mL

First, we will calculate the moles of base added and put that value in our SCF table.

25.00 mL × $\dfrac{1\ \text{L}}{1000\ \text{mL}} \times \dfrac{0.100\ \text{mol NaOH}}{1\ \text{L}} \times \dfrac{1\ \text{mol OH}^{-}}{1\ \text{mol NaOH}}$ = 0.00250 moles OH^–

OH^–(aq) + H₃O⁺(aq) → 2 H₂O(ℓ)

S (Start)

0.00250

–

C (Change)

F (Finish)

Then, we subtract whichever number of moles is smaller between the two reactants, ensuring that at least one reactant’s quantity goes to zero and other reactant’s remaining quantity is positive (or zero).

	OH^–(aq) + H₃O⁺(aq) → 2 H₂O(ℓ)
S (Start)	0.00250	0.00250	–
C (Change)	-0.00250	-0.00250	–
F (Finish)	0	0	–

Lastly, we ask ourselves “What’s in my beaker?”. In this case, all of our strong base and strong acid have reacted and all we have left is water. The pH of pure water is 7.00.

(d) added base = 37.50 mL

First, we will calculate the moles of base added and put that value in our SCF table.

37.50 mL × $\dfrac{1\ \text{L}}{1000\ \text{mL}} \times \dfrac{0.100\ \text{mol NaOH}}{1\ \text{L}} \times \dfrac{1\ \text{mol OH}^{-}}{1\ \text{mol NaOH}}$ = 0.00375 moles OH^–

OH^–(aq) + H₃O⁺(aq) → 2 H₂O(ℓ)

S (Start)

0.00375

0.00250

–

C (Change)

F (Finish)

Then, we subtract whichever number of moles is smaller between the two reactants, ensuring that at least one reactant’s quantity goes to zero and other reactant’s remaining quantity is positive.

	OH^–(aq) + H₃O⁺(aq) → 2 H₂O(ℓ)
S (Start)	0.00375	0.00250	–
C (Change)	-0.00250	-0.00250	–
F (Finish)	0.00125	0	–

Lastly, we ask ourselves “What’s in my beaker?”. In this case, we have excess strong base and need to calculate the new concentration of the hydroxide ion in order to calculate the resulting pH.

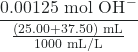$\dfrac{0.00125\ \text{mol OH}^{-}}{\frac{(25.00 + 37.50)\ \text{mL}}{1000\ \text{mL/L}}}$ = 0.0200 M OH^–

pOH = -log[OH^–] = 1.698
pH = 14.00 – pOH = 14.00 – 1.698 = 12.301

Check Your Learning
Calculate the pH for the strong acid/strong base titration between 50.0 mL of 0.100 M HNO₃(aq) and 0.200 M NaOH (titrant) at the listed volumes of added base: 0.00 mL, 15.0 mL, 25.0 mL, and 40.0 mL.

Answer:

Vol 0.00 mL: pH = 1.000
Vol 15.0 mL: pH = 1.5111
Vol 25.0 mL: pH = 7.000
Vol 40.0 mL: pH = 12.523

In the example, we calculated pH at four points during a titration. The most straightforward acid-base reactions are those of a strong acid with a strong base. Figure 2 shows data for the titration of a 25.0-mL sample of 0.100 M hydrochloric acid with 0.100 M sodium hydroxide, where the pH measured after successive additions of small amounts of NaOH are graphed in a form that is called a titration curve (graphing pH versus volume of titrant added). The pH increases slowly at first, increases rapidly in the middle portion of the curve, and then increases slowly again. The point of inflection (located at the midpoint of the vertical part of the curve) is the equivalence point for the titration. It indicates when equivalent quantities of acid and base are present. For the titration of a strong acid with a strong base, the equivalence point occurs at a pH of 7.00 since only water remains and [H₃O⁺] = [OH^–] = 1.0 × 10^-7 M. (see Example 1, part C).

The graph in this figure is titled “Titration of Strong Acid.” The horizontal axis is labeled “Volume of 0.100 M N a O H added (m L).” Markings and vertical gridlines are provided every 5 units from 0 to 50. The vertical axis is labeled “p H” and is marked every 1 units beginning at 0 extending to 14. A red curve is drawn on the graph which increases gradually from the point (0, 1) up to about (22.5, 2.2) after which the graph has a vertical section from (25, 4) up to nearly (25, 11). The graph then levels off to a value of about 12.4 from about 40 m L up to 50 m L. The midpoint of the vertical segment of the curve is labeled “Equivalence point p H, 7.00.” — **Figure 2.** The titration curve for the titration of 25.00 mL of 0.100 M HCl (strong acid) with 0.100 M NaOH (strong base) has an equivalence point of 7.00 pH.

Acid-Base Indicators

The equivalence point of a titration may be detected visually if a distinct change in the appearance of the sample solution accompanies the completion of the reaction. More commonly, special dyes called indicators are added to the sample solutions to impart a change in color at or very near the equivalence point of the titration. Equivalence points may also be detected by measuring some solution property that changes in a predictable way during the course of the titration (like the pH). Regardless of the approach taken to detect a titration’s equivalence point, the volume of titrant actually measured is called the end point. Properly designed titration methods typically ensure that the difference between the equivalence and end points is negligible.

Certain organic substances, such as phenolphthalein, which can be used to determine the pH of a solution, are called acid-base indicators. Acid-base indicators are either weak organic acids or weak organic bases. For example, phenolphthalein is a colorless substance in any aqueous solution with a hydronium ion concentration greater than 5.0 × 10⁻⁹M (pH < 8.3). In more basic solutions where the hydronium ion concentration is less than 5.0 × 10⁻⁹M (pH > 8.3), it is red or pink.

Another acid-base indicator is methyl orange, which is a weak acid. The equilibrium can be represented by an equation in which we use HIn as a simple representation for the complex methyl orange molecule:

HIn(aq) + H₂O(ℓ) ⇄ H₃O⁺(aq) + In^–(aq)
red yellow

K_a = $\dfrac{[\text{H}_{3}\text{O}^{+}][\text{In}^{-}]}{[\text{HIn}]}$ = 4.0 × 10^-4

The nonionized form, HIn, is red, and the anion of methyl orange, In⁻, is yellow. When we add acid to a solution of methyl orange, the increased hydronium ion concentration shifts the equilibrium toward the nonionized red form, in accordance with Le Châtelier’s principle. If we add base, we shift the equilibrium towards the yellow form. This behavior is completely analogous to the action of buffers.

There are many different acid-base indicators that cover a wide range of pH values and can be used to determine the approximate pH of an unknown solution by a process of elimination. Universal indicators and pH paper contain a mixture of indicators and exhibit different colors at different pHs. Figure 3 presents several indicators, their colors, and their color-change intervals.

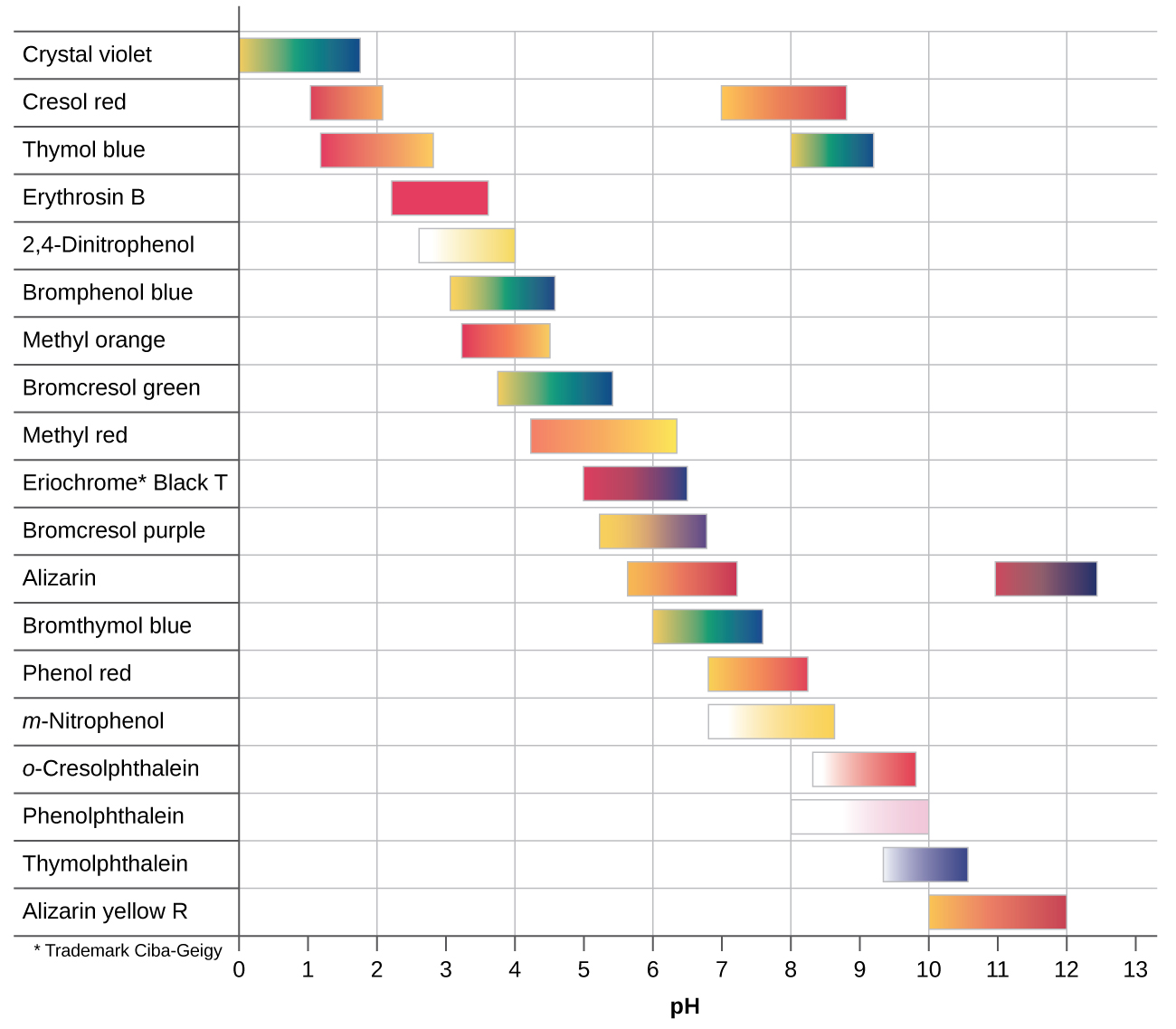
This figure provides a graphical representation of indicators and color ranges. A horizontal axis is labeled “p H.” This axis begins at zero and increases by ones up to 13. The left side of the graphic provides a column with the names of indicators. To the right of each indicator name is either one or two colored bars that are shaded according to the indicator color at various p H ranges. From the top, the first row is labeled “Crystal violet.” The associated colored bar is yellow at its left end at a p H of 0 and changes to green and blue moving right to its endpoint at a p H of 1.8. The second row is labeled “Cresol red.” The associated colored bar is red at its left end at a p H of 1 and changes to orange and yellow moving right to its endpoint at a p H of just over 2. A second bar to its right is yellow at a p H of around 7 and proceeds through orange to red at a p H of about 9. The third row is labeled “Thymol blue.” The associated colored bar is red at its left end at a p H of nearly 1.2 and changes to orange and red moving right to its endpoint at a p H of 2.8. A second bar begins in yellow at a p H of 8 and proceeds through green and blue to its end at a p H of around 9.1. The fourth row is labeled “Erythrosin B.” The associated colored bar is red from a p H of 2.2 to its endpoint at a p H of 3.6. The fifth row is labeled “2 comma 4 dash Dinitrophenol.” The associated colored bar is white at its left end at a p H of 2.6 and changes to yellow at its endpoint at a p H of 4. The sixth row is labeled “Bromophenol blue.” The associated colored bar is yellow at its left end at a p H of 3 and changes to green and blue moving right to its endpoint at a p H of 4.5. The seventh row is labeled “Methyl orange.” The associated colored bar is red-orange at its left end at a p H of 4.2 and changes to yellow moving right to its endpoint at a p H of 6.3. The eighth row is labeled “Bromocresol green.” The associated colored bar is yellow at its left end at a p H of 3.8 and changes to green and blue moving right to its endpoint at a p H of 5.4. The ninth row is labeled “Methyl red.” The associated colored bar is orange at its left end at a p H of 4.2 and changes to yellow moving right to its endpoint at a p H of 6.3. The tenth row is labeled “Eriochrome * Black T.” The associated colored bar is red at its left end at a p H of 5 and changes to purple and blue moving right to its endpoint at a p H of 6.5. The eleventh row is labeled “Bromocresol purple.” The associated colored bar is yellow at its left end at a p H of 5.2 and changes to purple moving right to its endpoint at a p H of 6.8. The twelfth row is labeled “Alizarin.” The first associated colored bar is yellow-orange at its left end at a p H of 5.7 and changes to red moving right to its endpoint at a p H of 7.2. A second bar begins in red at a p H of 11 and changes to purple, then dark blue at its right end at a p H of 12.4. The thirteenth row is labeled “Bromothymol blue.” The associated colored bar is yellow at its left end at a p H of 6 and changes to green and blue moving right to its endpoint at a p H of 7.6. The fourteenth row is labeled “Phenol red.” The associated colored bar is yellow-orange at its left end at a p H of 6.8 and changes to orange and red moving right to its endpoint at a p H of 8.2. The fifteenth row is labeled “m dash Nitrophenol.” The associated colored bar is white at its left end at a p H of 6.8 and changes to yellow moving right to its endpoint at a p H of 8.6. The sixteenth row is labeled “o dash Cresolphthalein.” The associated colored bar is white at its left end at a p H of 8.3 and changes to red moving right to its endpoint at a p H of 9.8. The seventeenth row is labeled “Phenolphthalein.” The associated colored bar is white at its left end at a p H of 8 and changes to pink moving right to its endpoint at a p H of 10. The eighteenth row is labeled “Thymolphthalein.” The associated colored bar is light blue at its left end at a p H of 9.3 and changes to a deep, dark blue moving right to its endpoint at a p H of 10.5. The nineteenth row is labeled “Alizarin yellow R.” The associated colored bar is yellow-orange at its left end at a p H of 10 and changes to red moving right to its endpoint at a p H of 12. — **Figure 3.** This chart illustrates the ranges of color change for several acid-base indicators.

Titration curves help us pick an indicator that will provide a sharp color change at the equivalence point. The best selection would be an indicator that has a color change interval that brackets the pH at the equivalence point of the titration.

The color change intervals of three indicators are shown in Figure 4. The equivalence points of both the titration of the strong acid and of the weak acid are located in the color-change interval of phenolphthalein. We can use it for titrations of either strong acid with strong base or weak acid with strong base.

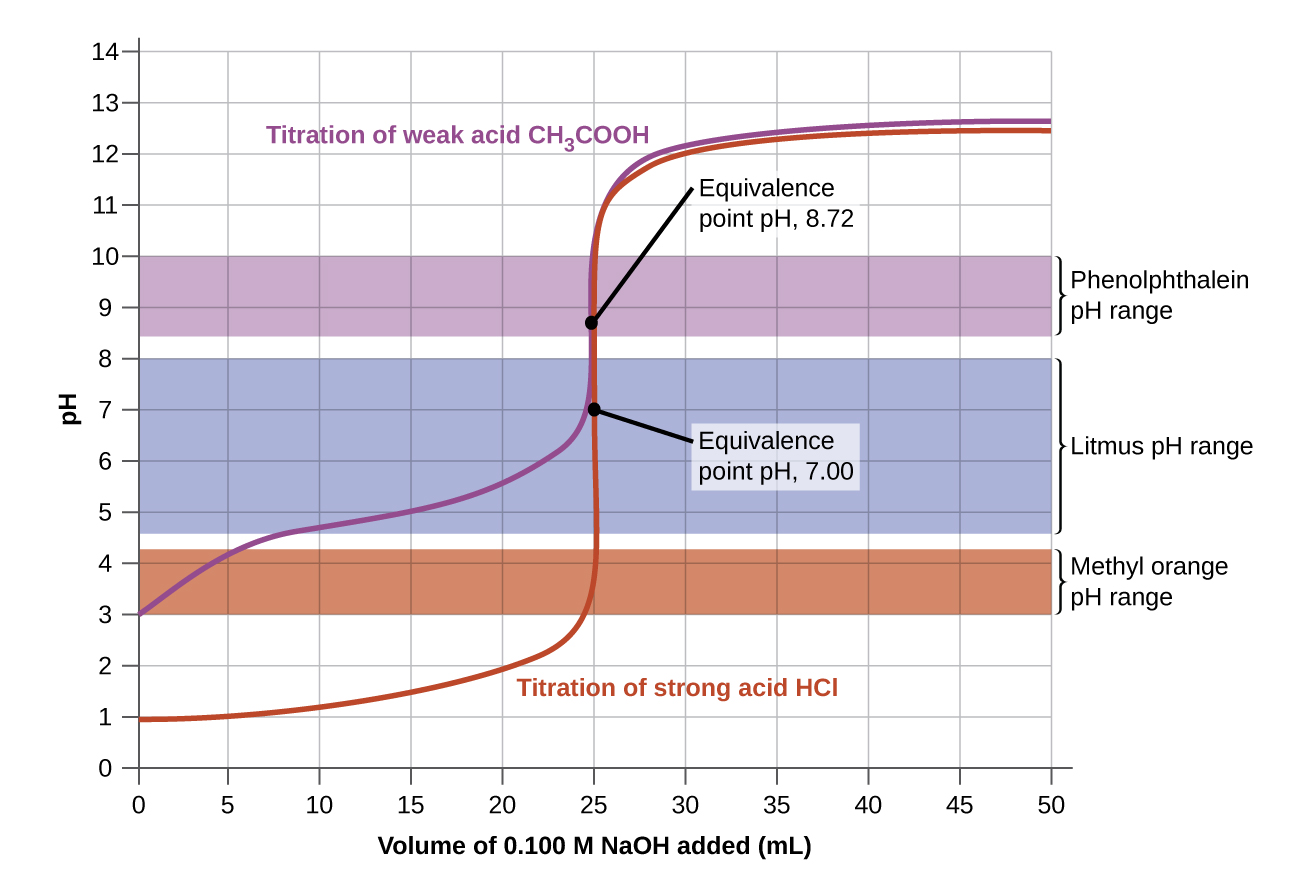
A graph is shown which is titled “Titration of Weak Acid.” The horizontal axis is labeled “Volume of 0.100 M N a O H added (m L)” and begins at 0 with markings every 5 units up to 50. The vertical axis is labeled “p H” and begins at 0 and increases by single units up to 14. A red curve is drawn on the graph. The curve begins at (0, 3) and passes through the points (5, 4.1), (10, 4.7), (15, 5), (20, 5.5), and (22.5, 6), after which it rapidly increases, forming a vertical section centered at the point (25, 8.7). The rapid increase of the curve then levels off and the curve passes through the points (30, 12), (35, 12.4), (40, 12.5), (45, 12.6), and (50, 12.6). A brown rectangle extends horizontally across the graph covering the p H of 3 to 4.2 range. To the right, this rectangle is labeled “Methyl orange p H range.” A blue rectangle extends horizontally across the graph covering the p H of 4.6 to 8 range. To the right, this rectangle is labeled “Litmus p H range.” A purple rectangle extends horizontally across the graph covering the p H of 8.4 to 10 range. To the right, this rectangle is labeled “Phenolphthalein p H range.” The midpoint of the vertical segment of the curve is labeled “Equivalence point p H, 8.72.” — **Figure 4.** The graph shows a titration curve for the titration of 25.00 mL of 0.100 M CH3COOH (weak acid) with 0.100 M NaOH (strong base) and the titration curve for the titration of HCl (strong acid) with NaOH (strong base). The pH ranges for the color change of phenolphthalein, litmus, and methyl orange are indicated by the shaded areas.

Litmus is a suitable indicator for the HCl titration because its color change brackets the equivalence point. However, we should not use litmus for the CH₃COOH titration because the pH is within the color-change interval of litmus when only about 12 mL of NaOH has been added, and it does not leave the range until 25 mL has been added. The color change would be very gradual, taking place during the addition of 13 mL of NaOH, making litmus useless as an indicator of the equivalence point.

We could use methyl orange for the HCl titration, but it would not give very accurate results: (1) It completes its color change slightly before the equivalence point is reached (but very close to it, so this is not too serious); (2) it changes color, as Figure 4 shows, during the addition of nearly 0.5 mL of NaOH, which is not so sharp a color change as that of litmus or phenolphthalein; and (3) it goes from yellow to orange to red, making detection of a precise endpoint much more challenging than the colorless to pink change of phenolphthalein. Figure 4 shows us that methyl orange would be completely useless as an indicator for the CH₃COOH titration. Its color change begins after about 1 mL of NaOH has been added and ends when about 8 mL has been added. The color change is completed long before the equivalence point (which occurs when 25.0 mL of NaOH has been added) is reached and hence provides no indication of the equivalence point.

Key Concepts and Summary

A titration analysis, typically an acid-base reaction, involves a solution of known concentration incrementally added to a solution of unknown concentration until the reaction is complete, also known as the equivalence point. If the pH is measured throughout the reaction, the pH can be plotted versus the volume of titrant added to create a titration curve. Indicators can be used that change color at a specific pH value, preferably near the equivalence point. The end point is the amount of titrant added when the color of the indicator changes.

Glossary

acid-base indicator: color indicators used in acid-base solutions that can be used to determine the pH of a solution

analyte: a substance whose concentration is to be measured

buret: a graduated glass tube used to add a solution in precise increments

end point: the volume of titrant added when the indicator changes color

equivalence point: the volume of titrant added when the moles of titrant added is equal to the moles of analyte during a titration

indicator: special dyes used during a titration that impart a change in color at or very near the equivalence point

titrant: a solution of known concentration

titration analysis: a chemical reaction that occurs by making incremental additions of a solution of known concentration to a substance whose concentration is to be measured

titration curve: a graph of pH versus volume of titrant added

Chemistry End of Section Exercises

What is the difference between an equivalence point and the end point in a titration?
In a general chemistry lab session, 50.0 mL 1.0 M HNO₃ is titrated with 0.5 M KOH.
1. Write the net ionic equation for the titration reaction that occurs when 50.0 mL of 1.0 M HNO₃ is titrated with 0.50 M KOH.
2. Are there spectator ions present? If so, what are they and how will they affect the pH?
3. What will the pH be at the equivalence point?
4. How many moles of KOH will be added to the analyte to reach the equivalence point?
5. How many mL of KOH will be added to the analyte to reach the equivalence point?
In a general chemistry lab session, 80.0 mL 0.800 M Ba(OH)₂ is titrated with 0.500 M HBr.
1. Write the net ionic equation for the titration reaction that occurs when 50.0 mL 0.800 MBa(OH)₂ is titrated with 0.500 M HBr.
2. Are there spectator ions present? If so, what are they and how will they affect the pH?
3. What will the pH be at the equivalence point?
4. How many moles of HBr will be added to the analyte to reach the equivalence point?
5. How many mL of HBr will be added to the analyte to reach the equivalence point?
40.0 mL of 0.080 M NaOH is titrated with 0.020 M HCl. Calculate the pH at the following points:
1. Initially, before any HCl has been added
2. When 80.0 mL HCl has been added
3. When 140.0 mL HCl has been added
4. When 160.0 mL HCl has been added
5. When 180.0 mL HCl has been added
6. When 200.0 mL HCl has been added
7. Sketch the titration curve that results from this titration
25.0 mL of a 0.125 M HI solution is titrated with a 0.075 M Ca(OH)₂ solution. How many mL must be added to get to the equivalence point?
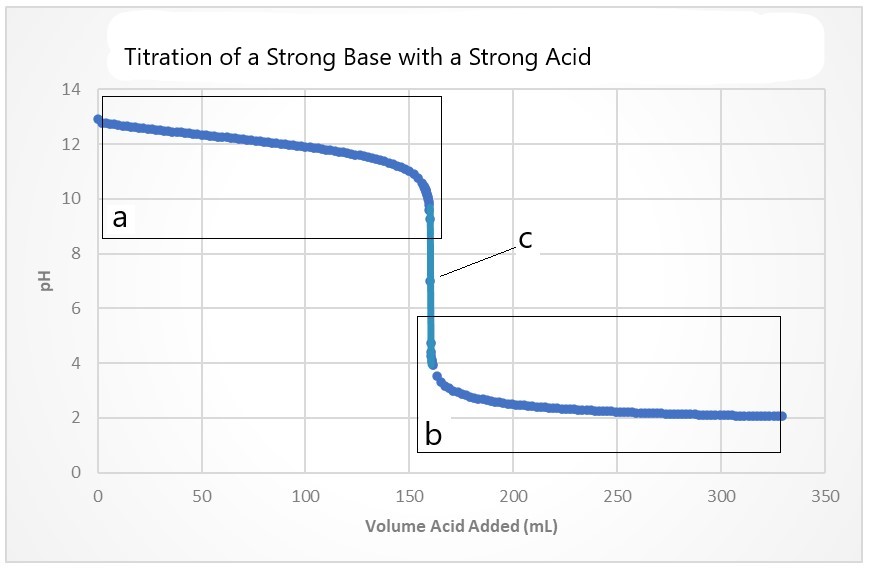
In the titration curve below, discuss each region of the titration curve in terms of concentrations of strong acid, strong base and pH:
For the titration of 50.0 mL 0.50 M KOH(aq) with 0.10 M HNO₃(aq), what are the coordinates (volume of HNO₃ added, pH) of the equivalence point?
25.00 mL of 1.00 M HCl reacts with the ammonia molecules in a sample of Cu(NH₃)₄SO₄·2H₂O. It is found by titration that 45.72 mL of 0.100 M NaOH is required to react with the excess HCl. How many moles of ammonia were in the original sample?
Methyl red is an acid-base indicator with K_a = 6.3 × 10^-6. The unionized form, HIn, is red, and the anionic form, In^–, is yellow. What is the color of a solution of methyl red at pH = 7.8?
1. Green
2. Red
3. Blue
4. Yellow
5. Orange

Answers to Chemistry End of Section Exercises

The equivalence point occurs when stoichiometric amount of titrant has been added to the analyte, that is the analyte and titrant have completely reacted and there is no excess amount of either. The end point occurs at the point in a titration when an indicator has undergone a visible change, often a color change. In a colorimetric titration, the observable change is a change in color owing to the addition of a small amount of indicator to the analyte solution. The goal in a colormetric titration is that the equivalence point of the titration and the end point of the indicator will be as close together as possible to minimize error.
(a) H₃O⁺(aq) + OH^–(aq) ⇌ 2 H₂O(ℓ)
(b) Yes, spectator ions are present.; K⁺ and NO₃^–; These are neutral ions and will not affect the pH.
(c) 7.00; All of the acid and base have reacted, leaving only water and neutral spectator ions.
(d) 0.050 mol KOH
(e) 1.0 × 10² mL
(a) H₃O⁺(aq) + OH^–(aq) ⇌ 2 H₂O(ℓ)
(b) Yes, spectator ions are present.; Ba²⁺ and Br^–; These are neutral ions and will not affect the pH.
(c) 7.00
(d) 0.128 mol HBr
(e) 256 mL
(a) 12.90; (b) 12.12; (c) 11.35; (d) 7.00 (equivalence point); (e) 2.74; (f) 2.48
(g)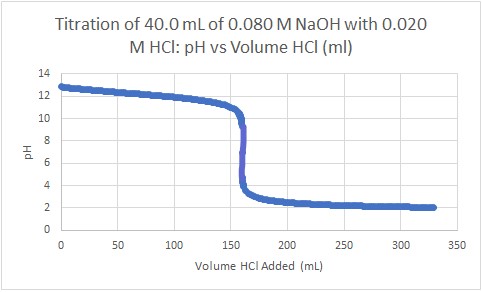
20.8 mL
(a) There is an excess of strong base, no strong acid, and pH>7
(b) There is an excess of strong acid, no strong base, and a pH<7
(c) All of the strong acid has completely reacted with the strong base so there is no strong acid, no strong base, and pH = 7.00
250.0 mL HNO₃ added, pH = 7.00
0.0204 mol NH₃
D

Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 103/104 Resource Book Copyright © by Chem 103 Textbook Team and Chem 104 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.