M15Q5: Weak Acid and Weak Base Calculations
Learning Objectives
- Calculate the pH of strong and weak acid and base solutions.
- Calculate the equilibrium concentrations of a monoprotic weak acid and its conjugate base, or a weak base and its conjugate acid.
- Calculate the percent ionization of a weak acid or base.
- Calculate the equilibrium constant for a monoprotic weak acid, Ka, or a weak base, Kb, given pH, [H3O+], or [OH–].
- Apply the relationship between Ka of a monoprotic acid and Kb of its conjugate base to problems as appropriate.
In this section, we will take what we have learned in the previous few sections and apply this knowledge to a variety of different chemistry problems, all involving weak acids and bases.
Example 1
The Product Ka × Kb = Kw
Given that the Kb for the nitrite ion, NO2–, is 2.17 × 10−11, calculate the Ka for its conjugate acid.
Solution
The conjugate acid of NO2– is HNO2; Ka for HNO2 can be calculated using the relationship:
Ka × Kb = 1.0 × 10-14 = Kw
Solving for Ka, we get:
Ka = ![]() =
= ![]() = 4.6 × 10-4
= 4.6 × 10-4
This answer can be verified by finding the Ka for HNO2 in Appendix I.
Check Your Learning
We can determine the relative acid strengths of NH4+ and HCN by comparing their ionization constants. The ionization constant of HCN is given in Appendix I as 3.3 × 10−10. The ionization constant of NH4+ is not listed, but the ionization constant of its conjugate base, NH3, is listed as 1.8 × 10−5. Determine the ionization constant of NH4+, and decide which is the stronger acid, HCN or NH4+.
Answer:
NH4+ is the slightly stronger acid (Ka for NH4+ = 5.6 × 10−10).
Example 2
Determination of Ka from Equilibrium Concentrations
Acetic acid is the principal ingredient in vinegar (Figure 1); that’s why it tastes sour. At equilibrium, a solution contains [CH3COOH] = 0.0787 M and [H3O+] = [CH3COO–] = 0.00118 M. What is the value of Ka for acetic acid?

Solution
We are asked to calculate an equilibrium constant from equilibrium concentrations. At equilibrium, the value of the equilibrium constant is equal to the reaction quotient for the reaction:
CH3COOH(aq) + H2O(ℓ) ⇌ H3O+(aq) + CH3COO–(aq)
Ka = ![]() = 1.77 × 10-5
= 1.77 × 10-5
Check Your Learning
What is the equilibrium constant for the ionization of the HSO4– ion, the weak acid used in some household cleansers:
HSO4–(aq) + H2O(ℓ) ⇌ H3O+(aq) + SO42-(aq)
In one mixture of NaHSO4 and Na2SO4 at equilibrium, [H3O+] = 0.027 M; [HSO4–] = 0.29 M; and [SO42-] = 0.13 M.
Answer:
Ka for HSO4– = 1.2 × 10-2
Example 3
Determination of Kb from Equilibrium Concentrations
Caffeine, C8H10N4O2 is a weak base. What is the value of Kb for caffeine if a solution at equilibrium has [C8H10N4O2] = 0.050 M, [C8H10N4O2H+] = 5.0 × 10−3 M, and [OH–] = 2.5 × 10−3 M?
Solution
At equilibrium, the value of the equilibrium constant is equal to the reaction quotient for the reaction:
C8H10N4O2(aq) + H2O(ℓ) ⇌ C8H10N4O2H+(aq) + OH–(aq)
Kb = ![]() = 2.5 × 10-4
= 2.5 × 10-4
Check Your Learning
What is the equilibrium constant for the ionization of the HPO42- ion, a weak base:
HPO42-(aq) + H2O(ℓ) ⇌ H2PO4–(aq) + OH–(aq)
In a solution containing a mixture of NaH2PO4 and Na2HPO4 at equilibrium, [OH–] = 1.3 × 10−6 M; [H2PO4–] = 0.042 M; and [HPO42-] = 0.341 M.
Answer:
Kb for HPO42- = 1.6 × 10-7
Example 4
Determination of Ka or Kb from pH
The pH of a 0.0516 M solution of nitrous acid, HNO2, is 2.34. What is its Ka?
HNO2(aq) + H2O(ℓ) ⇌ H3O+(aq) + NO2–(aq)
Solution
We determine an equilibrium constant starting with the initial concentrations of HNO2, H3O+, and NO2– as well as one of the final concentrations, the concentration of hydronium ion at equilibrium. (Remember that pH is simply another way to express the concentration of hydronium ion.)
We can solve this problem with the following steps in which x is a change in concentration of a species in the reaction:
pH → [H3O+]eq → x (in ICE table) → Calculate [HNO2]eq and [NO2–]eq → Ka
We can first create an ICE table for this reaction:
| HNO2(aq) + H2O(ℓ) ⇌ H3O+(aq) + NO2–(aq) | ||||
| I | 0.0516 | – | 0 | 0 |
| C | –x | – | +x | +x |
| E | 0.0516 – x | – | x | x |
Next, we can use the pH to find [H3O+]eq, which is “x” in our ICE table:
[H3O+]eq = 10-pH = 10-2.34 = 0.0046 M = x
| HNO2(aq) + H2O(ℓ) ⇌ H3O+(aq) + NO2–(aq) | ||||
| I | 0.0516 | – | 0 | 0 |
| C | -0.0046 | – | +0.0046 | +0.0046 |
| E | 0.0470 | – | 0.0046 | 0.0046 |
Finally, we calculate the value of the equilibrium constant using the data in the table:
Ka = ![]() = 4.5 × 10-4
= 4.5 × 10-4
Check Your Learning.
The pH of a solution of household ammonia, a 0.950 M solution of NH3, is 11.612. What is Kb for NH3.
Answer:
Kb = 1.8 × 10−5
Example 5
Equilibrium Concentrations in a Solution of a Weak Acid
Formic acid, HCO2H, is the irritant that causes the body’s reaction to ant stings (Figure 2).

What is the concentration of hydronium ion and the pH in a 0.534-M solution of formic acid?
HCOOH(aq) + H2O(ℓ) ⇌ H3O+(aq) + HCOO–(aq) Ka = 3.0 × 10-4
Solution
- Determine x and equilibrium concentrations. The equilibrium expression is:
HCOOH(aq) + H2O(ℓ) ⇌ H3O+(aq) + HCOO–(aq)
The concentration of water does not appear in the expression for the equilibrium constant, so we do not need to consider its change in concentration when setting up the ICE table.
The table shows initial concentrations (concentrations before the acid ionizes), changes in concentration, and equilibrium concentrations follows (the data given in the problem appear in color):
HCOOH(aq) + H2O(ℓ) ⇌ H3O+(aq) + HCOO–(aq) I 0.534 – 0 0 C –x – +x +x E 0.534 – x – x x - Solve for x and the equilibrium concentrations. At equilibrium:
Ka = 3.0 × 10-4 =
![Rendered by QuickLaTeX.com \dfrac{[\text{H}_{3}\text{O}^{+}][\text{HCOO}^{-}]}{[\text{HCOOH}]} = \dfrac{(x)(x)}{0.534 - x}](https://wisc.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-e49b265ecb7cfc03c538672d5e21edb8_l3.png)
Now solve for x. Because the initial concentration of acid is reasonably large and Ka is very small, we assume that x << 0.534, which permits us to simplify the denominator term as (0.534 − x) = 0.534. This gives:
Ka = 3.0 × 10-4 =
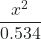
Solve for x as follows:
x2 = 0.534 × (3.0 × 10-4) = 1.6 × 10-4
x = (1.6 × 10-4)½ = 1.3 × 10-2 M
To check the assumption that x is small compared to 0.534, we calculate:
![]() =
= ![]() = 2.4 × 10-2 = 2.4%
= 2.4 × 10-2 = 2.4%
x is less than 5% of the initial concentration; the assumption is valid.
We find the equilibrium concentration of hydronium ion in this formic acid solution from its initial concentration and the change in that concentration as indicated in the last line of the table:
[H3O+] = ~0 + x = 0 + 1.3 × 10-2 M = 1.3 × 10-2 M
The pH of the solution can be found by taking the negative log of the [H3O+], so:
pH = -log[H3O+] = -log(1.3 × 10-2) = 1.89
Check Your Learning
Only a small fraction of a weak acid ionizes in aqueous solution. What is the percent ionization of acetic acid in a 0.100-M solution of acetic acid, CH3COOH?
CH3COOH(aq) + H2O(ℓ) ⇌ H3O+(aq) + CH3COO–(aq) Ka = 1.8 x 10-5
(Hint: Determine [CH3COO–] at equilibrium.) Recall that the percent ionization is the fraction of acetic acid that is ionized × 100%, or ![]() × 100%.
× 100%.
Answer:
percent ionization = 1.3%
The following example shows that the concentration of products produced by the ionization of a weak base can be determined by the same series of steps used with a weak acid.
Example 6
Equilibrium Concentrations in a Solution of a Weak Base
Find the concentration of hydroxide ion and the pH in a 0.25 M solution of trimethylamine, a weak base:
(CH3)3N(aq) + H2O(ℓ) ⇌ (CH3)3NH+(aq) + OH–(aq) Kb = 6.2 × 10-5
Solution
This problem requires that we calculate an equilibrium concentration by determining concentration changes as the ionization of a base goes to equilibrium. The solution is approached in the same way as that for the ionization of formic acid in Example 5. The reactants and products will be different and the numbers will be different, but the logic will be the same:

- Determine x and equilibrium concentrations. The table shows the changes and concentrations
(CH3)3N(aq) + H2O(ℓ) ⇌ (CH3)3NH+(aq) + OH–(aq) I 0.25 – 0 0 C –x – +x +x E 0.25 – x – x x - Solve for x and the equilibrium concentrations. At equilibrium:
Kb =
![Rendered by QuickLaTeX.com \dfrac{[(\text{CH}_{3})_{3}\text{NH}^{+}][\text{OH}^{-}]}{[(\text{CH}_{3})_{3}\text{N}]} = \dfrac{(x)(x)}{0.25 - x}](https://wisc.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-fc010515c4d292d926903a0541e949b5_l3.png) = 6.2 × 10-5
= 6.2 × 10-5If we assume that x is small relative to 0.25, then we can replace (0.25 − x) in the preceding equation with 0.25. Solving the simplified equation gives:
x = 3.9 × 10-3
This change is less than 5% of the initial concentration (0.25), so the assumption is justified.
Recall that, for this computation, x is equal to the equilibrium concentration of hydroxide ion in the solution (see earlier tabulation):
[OH–] = ~0 + x = x = 3.9 × 10-3 M
Then calculate pOH as follows:
pOH = -log[OH–] = -log(3.9 × 10-3) = 2.40
Using the relation introduced in the previous section of this chapter:
pH + pOH = pKw = 14.00
permits the computation of pH:
pH = 14.00 – pOH = 14.00 – 2.40 = 11.60
- Check the work. A check of our arithmetic shows that Kb = 6.2 × 10−5.
Check Your Learning
(a) Show that the calculation in Step 2 of this example gives an x of 3.9 × 10−3 and the calculation in Step 3 shows Kb = 6.2 × 10−5.
(b) Find the concentration of hydroxide ion in a 0.0325 M solution of ammonia, a weak base with a Kb of 1.77 × 10−5. Calculate the percent ionization of ammonia, the fraction ionized × 100%, or ![]() × 100%
× 100%
Answer:
7.58 × 10−4 M, 2.33%
Some weak acids and weak bases ionize to such an extent that the simplifying assumption that x is small relative to the initial concentration of the acid or base is inappropriate. As we solve for the equilibrium concentrations in such cases, we will see that we cannot neglect the change in the initial concentration of the acid or base, and we must solve the equilibrium equations by using the quadratic equation.
Example 7
Equilibrium Concentrations in a Solution of a Weak Acid
Sodium bisulfate, NaHSO4, is used in some household cleansers because it contains the HSO4– ion, a weak acid. What is the pH of a 0.50 M solution of HSO4−?
HSO4–(aq) + H2O(ℓ) ⇌ H3O+(aq) + SO42-(aq) Ka = 1.1 × 10-2
Solution
We need to determine the equilibrium concentration of the hydronium ion that results from the ionization of HSO4− so that we can use [H3O+] to determine the pH. As in the previous examples, we can approach the solution by the following steps:

- Determine x and equilibrium concentrations. This table shows the changes and concentrations:
HSO4–(aq) + H2O(ℓ) ⇌ H3O+(aq) + SO42-(aq) I 0.50 – 0 0 C –x – +x +x E 0.50 – x – x x - Solve for x and the concentrations. As we begin solving for x, we will find this is more complicated than in previous examples. As we discuss these complications we should not lose track of the fact that it is still the purpose of this step to determine the value of x.
At equilibrium:
Ka = 1.1 × 10-2 =
![Rendered by QuickLaTeX.com \dfrac{[\text{H}_{3}\text{O}^{+}][\text{SO}_{4}^{2-}]}{[\text{HSO}_{4}^{-}]} = \dfrac{(x)(x)}{0.50 - x}](https://wisc.pb.unizin.org/app/uploads/quicklatex/quicklatex.com-de4965a50a07abf9ab35dd334c464e26_l3.png)
If we assume that x is small and approximate (0.50 − x) ≈ 0.50, we find:
1.1 × 10-2 =
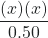
x = 7.4 × 10-2 M
When we check the assumption, we calculate:
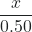 =
= 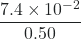 = 0.15 = 15%
= 0.15 = 15%The value of x is not less than 5% of 0.50, so the assumption is not valid. We need the quadratic formula to find x.
The equation:
Ka = 1.1 × 10-2 =
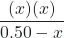
gives
(1.1 × 10-2)(0.50 – x) = x2
x2 + (1.1 × 10-2)x – (5.5 × 10-3) = 0This equation can be solved using the quadratic formula. Solving for x gives a negative root (which cannot be correct since concentration cannot be negative) and a positive root:
x = 6.9 × 10-2
Now determine the hydronium ion concentration and the pH:
[H3O+] = 0 + x = 0 + 6.9 × 10-2 = 6.9 × 10-2 M
The pH of this solution is:
pH = -log[H3O+] = -log(6.9 × 10-2) = 1.16
Check Your Learning
(a) Show that the quadratic formula gives x = 6.9 × 10−2.
(b) Calculate the pH in a 0.010-M solution of caffeine, a weak base:
C8H10N4O2(aq) + H2O(ℓ) ⇌ C8H10N4O2+(aq) + OH–(aq) Kb = 2.5 × 10-4
(Hint: It will be necessary to convert [OH–] to [H3O+] or pOH to pH toward the end of the calculation.)
Answer:
pH = 11.16
Key Concepts and Summary
In this section, we give many common examples of acid/base quantitative problems. Each example solves for a different variable, some using only the equilibrium expressions (Examples 1-3), but others require you to set up an ICE table during the course of solving the problem (Examples 4-7). We highly recommend you work through these examples and and try the “Check Your Learning” exercise to ensure that you have learned the concept. All of these examples are very common problems you might see on your graded assessments!
Chemistry End of Section Exercises
- What is the ionization constant, Ka, at 25 °C for the weak acid CH3NH3+, given that the Kb of the weak base CH3NH2 is 5.0 × 10−4?
- What is the ionization constant of the conjugate base of HNO2, given that the Ka of HNO2 is 7.4 × 10-4?
- Describe the method to find the pH of a benzoic acid, C6H5COOH, solution with a known concentration. How does this differ from the method to find the pH of an HCl solution of known concentration?
- What is the pH of a 0.750 M C6H5COOH solution? (Ka = 1.2 × 10-4)
- What is the pH of a 1.25 CH3NH2 solution? (Kb = 5.0 × 10-4)
- What is the pH of a 0.0500 M C6H5NH3+ solution? (Kb of C6H5NH2 = 3.9 × 10-10)
- Propanoic acid, C2H5COOH (Ka = 1.33 × 10−5), is used in the manufacture of calcium propanoate, a food preservative. What is the hydronium ion concentration in a 0.698 M solution of C2H5COOH? What is the pH?
- The pH of a 0.20-M solution of a weak acid, HA, is 1.933. Determine Ka for HA from these data.
- The pH of a solution of household ammonia, a 0.950 M solution of NH3, is 11.612. Determine Kb for NH3 from these data.
- The ionization constant of lactic acid, CH3CH(OH)COOH, an acid found in the blood after strenuous exercise, is 1.36 × 10−4. If 20.0 g of lactic acid is used to make a solution with a volume of 1.00 L, what is the pH of the solution?
- White vinegar is a 5.0% by mass solution of acetic acid, CH3COOH, in water. If the density of white vinegar is 1.007 g/cm3, what is the pH? The Ka of CH3COOH is 1.8 × 10-5.
- What is the pH of 0.10 M sodium acetate? (Ka Acetic acid, CH3COOH = 1.8 × 10-5)
- What is the percent ionization of a 0.20 M HF(aq) solution? (Ka for HF = 7.2 × 10–4)
- The pH of an unknown 0.0100M solution is 3.25. Which of the following could be true about the solution?
- It is a strong acid.
- It is a strong base.
- It is a weak acid.
- It is a weak base.
- A Ka value or other information is needed to answer this question.
- Chloroacetic acid, CH2ClCOOH, is a weak acid with Ka = 1.4 × 10–3. Which of the following describes the relative concentrations of the chemical species found in a 0.10 M aqueous solution of chloroacetic acid?
- H2O >> CH2ClCOOH > H3O+ ≈ CH2ClCOO– >> OH–
- H2O >> CH2ClCOOH > H3O+ ≈ OH– >> CH2ClCOO–
- H2O >> CH2ClCOO– > H3O+ ≈ OH– >> CH2ClCOOH
- H2O >> CH2ClCOO– ≈ CH2ClCOOH > H3O+ ≈ OH–
- H2O >> CH2ClCOO– ≈ CH2ClCOOH > H3O+ >> OH–
- Use the table below to answer the following questions.
Name Formula Ka Acetic acid CH3COOH 1.8 × 10–5 Formic acid HCOOH 3.0 × 10–4 Hydrazoic acid HN3 1.0 × 10–5 Hypochlorous acid HOCl 6.8 × 10–8 - Rank the following solutions in order from the lowest to highest pH: 0.10 M CH3COO–, 0.10 M HCOO–, 0.10 M N3–, 0.10 M OCl–.
- Rank the following solutions in order from the lowest to highest percent ionization: 0.0010 HCOOH, 0.10 M HOCl, 0.0010 M HOCl.
Answers to Chemistry End of Section Exercises
- 2.0 × 10-11
- The conjugate base is NO2–, with Kb = 1.4 × 10-11.
- H2C2O4 is a weak acid and will not completely dissociate in water. The equilibrium H3O+ concentration must be found using an ICE table and the Ka value for the weak acid. Once the equilibrium H3O+ concentration is found, the pH can be determined by calculating -log[H3O+]. HCl is a strong acid and will dissociate completely in water so an ICE table is not necessary to find the H3O+ concentration. It is equal to the original HCl concentration. The pH can be determined by calculating -log [HCl].
- pH = 2.0515
- pH = 12.40
- pH = 2.946
- [H3O+] = 0.00305 M; pH = 2.52
- [H3O+] = 0.01167 M; Ka = 7.2 × 10-4
- Kb = 1.77 × 10-5
- pH = 2.260
- pH = 2.41
- pH = 8.87
- 6.0%
- C
- A
- (a) 0.10 M HCOO– < 0.10 M CH3COO– < 0.10 M N3– < 0.10 M OCl–
(b) 0.10 M HOCl < 0.0010 M HOCl < 0.0010 M HCOOH
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

