M16Q7: Solubility
Learning Objectives
- Recognize the difference between a saturated and unsaturated solution.
- Describe the establishment of equilibrium between a sparingly soluble salt and water, and write the solubility product (Ksp) expression for the dissolution of the salt.
- Determine the solubility of a salt from a Ksp value and vice versa.
| Ksp and Solubility | - Describe the effect of a common ion on the solubility of a salt and calculate the solubility of the salt in a solution containing a common ion.
| Common Ion Effect | - Predict the effect of pH on the solubility of salts.
- Use the reaction quotient, Q, to predict whether a precipitate will form.
| Q & Solubility |
| Key Concepts and Summary | Glossary | End of Section Exercises |

We previously learned about aqueous solutions and solubility rules. While these rules give us a rough picture of solubility, a more detailed description is necessary to understand several important aspects of solubility in aqueous systems. Solubility equilibrium, which we will explore in this chapter, is a more complex topic that allows us to determine the extent to which a slightly soluble ionic solid will dissolve, and the conditions under which precipitation (such as the fluorite deposit in Figure 1) will occur.
The preservation of medical laboratory blood samples, mining of sea water for magnesium, formulation of over-the-counter medicines such as Milk of Magnesia and antacids, and treating the presence of hard water in your home’s water supply are just a few of the many tasks that involve controlling the equilibrium between a slightly soluble ionic solid and an aqueous solution of its ions.
In this section, we will find out how we can control the dissolution of a slightly soluble ionic solid by the application of Le Châtelier’s principle. However, we will first learn how to use the equilibrium constant of the reaction to determine the concentration of ions present in a solution.
The Solubility Product Constant
Silver chloride is what’s known as a sparingly soluble ionic solid (Figure 2). Recall from the solubility rules in an earlier chapter that halides of Ag+ are not normally soluble. However, when we add an excess of solid AgCl to water, it dissolves to a small extent and produces a mixture consisting of a very dilute solution of Ag+ and Cl– ions in equilibrium with undissolved silver chloride:
This equilibrium, like other equilibria, is dynamic; some of the solid AgCl continues to dissolve, but at the same time, Ag+ and Cl– ions in the solution combine to produce an equal amount of the solid. At equilibrium, the opposing processes have equal rates.
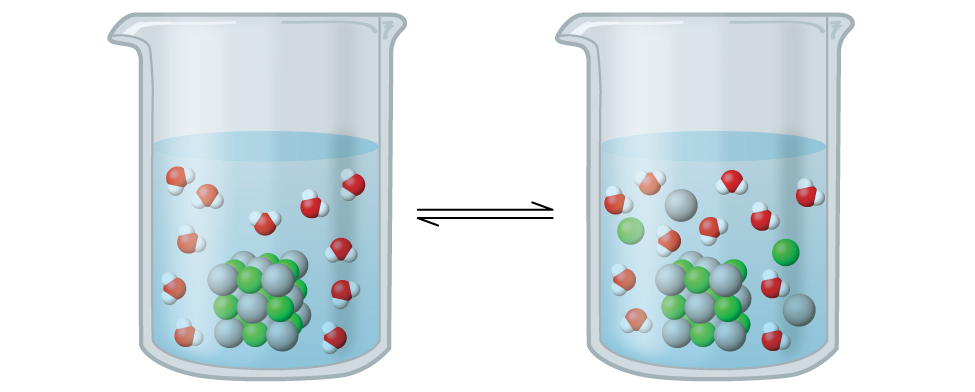
The equilibrium constant for the equilibrium between a slightly soluble ionic solid and a solution of its ions is called the solubility product (Ksp) of the solid. For silver chloride, at equilibrium:
AgCl(s) ⇌ Ag+(aq) + Cl–(aq) Ksp = [Ag+][Cl–]
When looking at dissolution reactions such as this, the solid is listed as a reactant, whereas the ions are listed as products. The solubility product constant, as with every equilibrium constant expression, is written as the product of the concentrations of each of the ions, raised to the power of their stoichiometric coefficients. Here, the solubility product constant is equal to Ag+ and Cl– when a solution of silver chloride is in equilibrium with undissolved AgCl. There is no denominator representing the reactants in this equilibrium expression since the reactant is a pure solid; therefore [AgCl] does not appear in the expression for Ksp.
Some common solubility products are listed in Table 1 according to their Ksp values (a more extensive compilation of products appears in Appendix J). Each of these equilibrium constants is much smaller than 1 because the compounds listed are only slightly soluble. A small Ksp represents a system in which the equilibrium lies to the left, so that relatively few hydrated ions would be present in a saturated solution.
| Substance | Ksp at 25 °C |
| CuCl | 1.2 × 10–6 |
| CuBr | 5.3 × 10–9 |
| AgI | 8.3 × 10–17 |
| PbS | 7 × 10–29 |
| Al(OH)3 | 1.3 × 10–33 |
| Fe(OH)3 | 4 × 10–38 |
Example 1
Writing Equations and Solubility Products
Write the ionic equation for the dissolution and the solubility product expression for each of the following slightly soluble ionic compounds:
- AgI, silver iodide, a solid with antiseptic properties
- CaCO3, calcium carbonate, the active ingredient in many over-the-counter chewable antacids
- Mg(OH)2, magnesium hydroxide, the active ingredient in Milk of Magnesia
- Mg(NH4)PO4, magnesium ammonium phosphate, an essentially insoluble substance used in tests for magnesium
- Ca5(PO4)3OH, the mineral apatite, a source of phosphate for fertilizers
(Hint: When determining how to break (d) and (e) up into ions, refer to the list of polyatomic ions in the section on chemical nomenclature.)
Solution
(a) AgI(s) ⇌ Ag+(aq) + I–(aq) Ksp = [Ag+][I–]
(b) CaCO3(s) ⇌ Ca2+(aq) + CO32-(aq) Ksp = [Ca2+][CO32-]
(c) Mg(OH)2(s) ⇌ Mg2+(aq) + 2 OH–(aq) Ksp = [Mg2+][OH–]2
(d) Mg(NH4)PO4(s) ⇌ Mg2+(aq) + NH4+(aq) + PO43-(aq) Ksp = [Mg2+][NH4+][PO43-]
(e) Ca5(PO4)3OH(s) ⇌ 5 Ca2+(aq) + 3 PO43-(aq) + OH–(aq)
Ksp = [Ca2+]5[PO43-]3[OH–]
Check Your Learning
Write the ionic equation for the dissolution and the solubility product for each of the following slightly soluble compounds:
- BaSO4
- Ag2SO4
- Al(OH)3
- Pb(OH)Cl
Answer:
(a) BaSO4(s) ⇌ Ba2+(aq) + SO42-(aq) Ksp = [Ba2+][SO42-]
(b) Ag2SO4(s) ⇌ 2 Ag+(aq) + SO42-(aq) Ksp = [Ag+]2[SO42-]
(c) Al(OH)3(s) ⇌ Al3+(aq) + 3 OH–(aq) Ksp = [Al3+][OH–]3
(d) Pb(OH)Cl(s) ⇌ Pb2+(aq) + OH–(aq) + Cl–(aq) Ksp = [Pb2+][OH–][Cl–]
Now we will extend the discussion of Ksp and show how the solubility product constant is determined from the solubility of its ions, as well as how Ksp can be used to determine the molar solubility of a substance.
Ksp and Solubility
Recall that the definition of solubility is the maximum possible concentration of a solute in a solution at a given temperature and pressure. We can determine the solubility product of a slightly soluble solid from that measure of its solubility at a given temperature and pressure, provided that the only significant reaction that occurs when the solid dissolves is its dissociation into solvated ions. In this case, we calculate the solubility product by taking the solid’s solubility expressed in units of moles per liter (mol/L), known as its molar solubility.
Example 2
Calculation of Ksp from Equilibrium Concentrations
We began this section with an example of the mineral, fluorite. Fluorite, CaF2, is a slightly soluble solid that dissolves according to the equation:
CaF2(s) ⇌ Ca2+(aq) + 2 F–(aq)
The concentration of Ca2+ in a saturated solution of CaF2 is 2.15 × 10–4 M; therefore, that of F– is 4.30 × 10–4 M, that is, twice the concentration of Ca2+. What is the solubility product of fluorite?
Solution
First, write out the Ksp expression, then substitute in concentrations and solve for Ksp:
CaF2(s) ⇌ Ca2+(aq) + 2 F–(aq)
A saturated solution is a solution at equilibrium with the solid. Thus:
Ksp = [Ca2+][F–]2 = (2.1 × 10-4)(4.3 × 10-4)2 = 3.98 × 10-11
As with other equilibrium constants, we do not include units with Ksp.
Check Your Learning
In a saturated solution that is in contact with solid Mg(OH)2, the concentration of Mg2+ is 1.31 × 10–4M. What is the solubility product for Mg(OH)2?
Mg(OH)2(s) ⇌ Mg2+(aq) + 2 OH–(aq)
Answer:
8.99 × 10–12
Example 3
Determination of Molar Solubility from Ksp
The Ksp of copper(I) bromide, CuBr, is 5.3 × 10–9. Calculate the molar solubility of copper bromide.
Solution
The solubility product constant of copper(I) bromide is 5.3 × 10–9.
The reaction is:
CuBr(s) ⇌ Cu+(aq) + Br–(aq)
First, write out the solubility product equilibrium constant expression:
Ksp = [Cu+][Br–]
Create an ICE table (as introduced in the chapter on fundamental equilibrium concepts), leaving the CuBr column empty as it is a solid and does not contribute to the Ksp:
| CuBr(s) ⇌ Cu+(aq) + Br–(aq) | |||
| I: Initial concentration (M) | – | 0 | 0 |
| C: Change (M) | – | +x | +x |
| E: Equilibrium concentration (M) | – | x | x |
At equilibrium:
Ksp = [Cu+][Br–]
5.3 × 10-9 = (x)(x) = x2
x = (5.3 × 10-9)½ = 7.3 × 10-5
Therefore, the molar solubility of CuBr is 7.3 × 10–5 M.
Check Your Learning
The Ksp of AgI is 8.3 × 10–17. Calculate the molar solubility of silver iodide.
Answer:
9.1 × 10–9 M
Example 4
Determination of Molar Solubility from Ksp, Part II
The Ksp of calcium hydroxide, Ca(OH)2, is 5.5 × 10–6. Calculate the molar solubility of calcium hydroxide.
Solution
The solubility product constant of calcium hydroxide is 5.5 × 10–6.
The reaction is:
Ca(OH)2(s) ⇌ Ca2+(aq) + 2 OH–(aq)
First, write out the solubility product equilibrium constant expression:
Ksp = [Ca2+][OH–]2
Create an ICE table, leaving the Ca(OH)2 column empty as it is a solid and does not contribute to the Ksp:
| Ca(OH)2(s) ⇌ Ca2+(aq) + 2 OH–(aq) | |||
| I: Initial concentration (M) | – | 0 | 0 |
| C: Change (M) | – | +x | +2x |
| E: Equilibrium concentration (M) | – | x | 2x |
At equilibrium:
Ksp = [Ca2+][OH–]2
5.5 × 10-6 = (x)(2x)2 = (x)(4x2) = 4x3
x = ![]() = 1.1 × 10-2
= 1.1 × 10-2
Therefore, the molar solubility of Ca(OH)2 is 1.1 × 10–2 M.
Check Your Learning
The Ksp of PbI2 is 7.1 × 10–9. Calculate the molar solubility of lead(II) iodide.
Answer:
1.2 × 10–3 M
Note that solubility is not always given as a molar value. When the solubility of a compound is given in some unit other than moles per liter, we must convert the solubility into moles per liter (i.e., molarity) in order to use it in the solubility product constant expression. Example 5 shows how to perform those unit conversions before determining the solubility product equilibrium.
Example 5
Determination of Ksp from Gram Solubility
Many of the pigments used by artists in oil-based paints (Figure 3) are sparingly soluble in water. For example, the solubility of the artist’s pigment chrome yellow, PbCrO4, is 4.6 × 10–6 g/L. Determine the solubility product equilibrium constant for PbCrO4.

Solution
We are given the solubility of PbCrO4 in grams per liter. If we convert this solubility into moles per liter, we can find the equilibrium concentrations of Pb2+ and CrO42-, then Ksp:
![This figure shows four horizontally oriented rectangles. The first three from the left are shaded green and the last one at the right is shaded white. Right pointing arrows between the rectangles are labeled “1,” “2,” and “3” moving left to right across the diagram. The first rectangle is labeled “Solubility of P b C r O subscript 4, in g divdided by L.” The second rectangle is labeled “[ P b C r O subscript 4 ], in m o l divided by L.” The third is labeled “[ P b superscript 2 plus] and [ C r O subscript 4 superscript 2 negative ].” The fourth rectangle is labeled “K subscript s p.”](https://wisc.pb.unizin.org/app/uploads/sites/557/2020/10/CNX_Chem_15_01_PbCrO4_img.jpg)
- Use the molar mass of PbCrO4
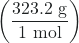 to convert the solubility of PbCrO4 in grams per liter into moles per liter:
to convert the solubility of PbCrO4 in grams per liter into moles per liter:
[PbCrO4] =
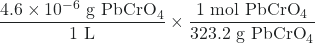 = 1.4 ×10-8 M PbCrO4
= 1.4 ×10-8 M PbCrO4 - The chemical equation for the dissolution indicates that 1 mol of PbCrO4 gives 1 mol of Pb2+(aq) and 1 mol of CrO42-(aq):
PbCrO4(s) ⇌ Pb2+(aq) + CrO42-(aq)
Thus, both [Pb2+] and [CrO42-] are equal to the molar solubility of PbCrO4:
[Pb2+] = [CrO42-] = 1.4 × 10-8 M - Solve. Ksp = [Pb2+][CrO42-] = (1.4 × 10–8)(1.4 × 10–8) = 2.0 × 10–16
Check Your Learning
The solubility of TlCl [thallium(I) chloride], an intermediate formed when thallium is being isolated from ores, is 3.46 grams per liter at 20 °C. What is its solubility product?
Answer:
2.08 × 10–4
Chemistry in Real Life: Using Barium Sulfate for Medical Imaging
Various types of medical imaging techniques are used to aid diagnoses of illnesses in a noninvasive manner. One such technique utilizes the ingestion of a barium compound before taking an X-ray image. A suspension of barium sulfate, a chalky powder, is ingested by the patient. Since the Ksp of barium sulfate is 1.1 × 10–10, very little of it dissolves as it coats the lining of the patient’s intestinal tract. Barium-coated areas of the digestive tract then appear on an X-ray as white, allowing for greater visual detail than a traditional X-ray (Figure 4).
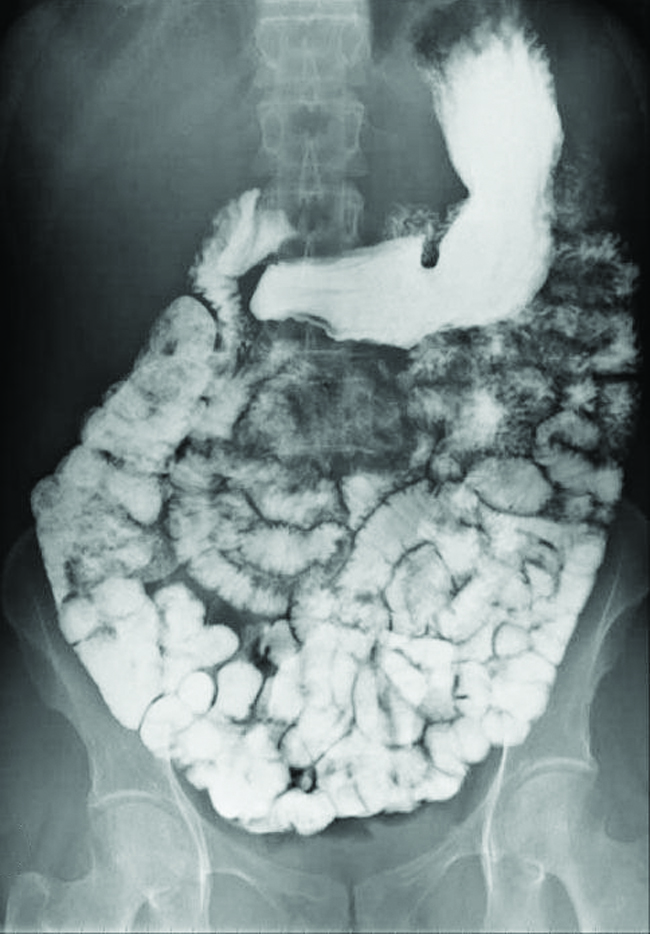
Further diagnostic testing can be done using barium sulfate and fluoroscopy. In fluoroscopy, a continuous X-ray is passed through the body so the doctor can monitor, on a TV or computer screen, the barium sulfate’s movement as it passes through the digestive tract. Medical imaging using barium sulfate can be used to diagnose acid reflux disease, Crohn’s disease, and ulcers in addition to other conditions.
Visit this website for more information on how barium is used in medical diagnoses and which conditions it is used to diagnose.
Predicting Precipitation
Tabulated Ksp values can also be compared to reaction quotients calculated from experimental data to predict whether a solid will precipitate in a reaction under specific conditions: Q equals Ksp at equilibrium; if Q is less than Ksp, the solid will dissolve until Q equals Ksp; if Q is greater than Ksp, precipitation will occur at a given temperature until Q equals Ksp.
The equation that describes the equilibrium between solid calcium carbonate and its solvated ions is:
CaCO3(s) ⇌ Ca2+(aq) + CO32-(aq)
We can establish this equilibrium either by adding solid calcium carbonate to water or by mixing a solution that contains calcium ions with a solution that contains carbonate ions. If we add calcium carbonate to water, the solid will dissolve until the concentrations are such that the value of the reaction quotient (Q = [Ca2+][CO32-]) is equal to the solubility product (Ksp = 8.7 × 10–9). If we mix a solution of calcium nitrate, which contains Ca2+ ions, with a solution of sodium carbonate, which contains CO32- ions, the slightly soluble ionic solid, CaCO3, will precipitate, provided that the concentrations of Ca2+ and CO32- ions make Q is greater than Ksp for the mixture. The reaction shifts to the left and the concentrations of the ions are reduced by formation of the solid until the value of Q equals Ksp. A saturated solution in equilibrium with the undissolved solid will result. If the concentrations are such that Q is less than Ksp, then the solution is not saturated and no precipitate will form.
We can compare numerical values of Q with Ksp to predict whether precipitation will occur, as Example 6 shows. (Note: Since all forms of equilibrium constants are temperature dependent, we will assume a room temperature environment going forward in this chapter unless a different temperature value is explicitly specified.)
Example 6
Precipitation of Mg(OH)2
The first step in the preparation of magnesium metal is the precipitation of Mg(OH)2 from sea water by the addition of lime, Ca(OH)2, a readily available inexpensive source of OH– ion:
Mg(OH)2(s) ⇌ Mg2+(aq) + 2 OH–(aq) Ksp = 1.8 ×10-11
The concentration of Mg2+(aq) in sea water is 0.0537 M. Will Mg(OH)2 precipitate when enough Ca(OH)2 is added to give a [OH–] of 0.0010 M?
Solution
This problem asks whether the reaction:
Mg(OH)2(s) ⇌ Mg2+(aq) + 2 OH–(aq)
shifts to the left and forms solid Mg(OH)2 when [Mg2+] = 0.0537 M and [OH–] = 0.0010 M. The reaction shifts to the left if Q is greater than Ksp. Calculation of the reaction quotient under these conditions is shown here:
Q = [Mg2+][OH–]2 = (0.0537)(0.0010)2 = 5.4 × 10-8
Because Q is greater than Ksp (Q = 5.4 × 10–8 is larger than Ksp = 1.8 × 10–11), we can expect the reaction to shift to the left and form solid magnesium hydroxide. Mg(OH)2(s) forms until the concentrations of magnesium ion and hydroxide ion are reduced sufficiently so that the value of Q is equal to Ksp.
Check Your Learning
Use the solubility product in Appendix J to determine whether CaHPO4 will precipitate from a solution with [Ca2+] = 0.0001 M and [HPO42-] = 0.001 M.
Answer:
No precipitation of CaHPO4; Q = 1 × 10–7, which is equal to Ksp.
In the previous example, we saw that Mg(OH)2 precipitated when Q is greater than Ksp. In general, when a solution of a soluble salt of the Mm+ ion is mixed with a solution of a soluble salt of the Xn– ion, the solid, MpXq precipitates if the value of Q for the mixture of Mm+ and Xn– is greater than Ksp for MpXq. Thus, if we know the concentration of one of the ions of a slightly soluble ionic solid and the value for the solubility product of the solid, then we can calculate the concentration that the other ion must exceed for precipitation to begin. To simplify the calculation, we will assume that precipitation begins when the reaction quotient becomes equal to the solubility product constant.
Example 7
Precipitation of Calcium Oxalate
Blood will not clot if calcium ions are removed from its plasma. Some blood collection tubes contain salts of the oxalate ion, C2O42-, for this purpose (Figure 5). At sufficiently high concentrations, the calcium and oxalate ions form solid, CaC2O4·H2O (which also contains water bound in the solid). The concentration of Ca2+ in a sample of blood serum is 2.2 × 10–3 M. What concentration of C2O42- ion must be established before CaC2O4·H2O begins to precipitate?
Solution
The equilibrium expression is:
CaC2O4(s) ⇌ Ca2+(aq) + C2O42-(aq)
For this reaction:
Ksp = [Ca2+][C2O42-] = 4 × 10-9
(see Appendix J)
CaC2O4 does not appear in this expression because it is a solid. Water does not appear because it is the solvent.
Solid CaC2O4 does not begin to form until Q equals Ksp. Because we know Ksp and [Ca2+], we can solve for the concentration of C2O42- that is necessary to produce the first trace of solid:
Q = Ksp = [Ca2+][C2O42-] = 4 × 10-9
(2.2 × 10-3)[C2O42-] = 4 × 10-9
[C2O42-] = ![]() = 1.8 ×10-6
= 1.8 ×10-6
A concentration of [C2O42-] = 1.8 × 10–6 M is necessary to initiate the precipitation of CaC2O4 under these conditions.
Check Your Learning
If a solution contains 0.0020 mol of CrO42- per liter, what concentration of Ag+ ion must be reached by adding solid AgNO3 before Ag2CrO4 begins to precipitate? Neglect any increase in volume upon adding the solid silver nitrate. (Ksp Ag2CrO4 is 1.1 × 10-12)
Answer:
2.3 × 10–5 M
It is sometimes useful to know the concentration of an ion that remains in solution after precipitation. We can use the solubility product for this calculation too: If we know the value of Ksp and the concentration of one ion in solution, we can calculate the concentration of the second ion remaining in solution. The calculation is of the same type as that in Example 8—calculation of the concentration of a species in an equilibrium mixture from the concentrations of the other species and the equilibrium constant. However, if the concentrations are different; we are calculating concentrations after precipitation is complete, rather than at the start of precipitation.
Example 8
Concentrations Following Precipitation
Clothing washed in water that has a manganese [Mn2+(aq)] concentration exceeding 0.1 mg/L (1.8 × 10–6 M) may be stained by the manganese upon oxidation, but the amount of Mn2+ in the water can be reduced by adding a base. If a person doing laundry wishes to add a buffer to keep the pH high enough to precipitate the manganese as the hydroxide, Mn(OH)2, what pH is required to keep [Mn2+] equal to 1.8 × 10–6 M?
Solution
The dissolution of Mn(OH)2 is described by the equation:
Mn(OH)2(s) ⇌ Mn2+(aq) + 2 OH–(aq) Ksp = 1.9 × 10-13
We need to calculate the concentration of OH– when the concentration of Mn2+ is 1.8 × 10–6 M. From that, we calculate the pH. At equilibrium:
Ksp = [Mn2+][OH–]2
1.9 × 10-13 = (1.8 × 10-6)[OH–]2
[OH–] = 3.3 × 10-4 M
Now we calculate the pH from the pOH:
pOH = -log[OH–] = -log(3.3 × 10-4) = 3.48
pH = 14.00 – pOH = 14.00 – 3.48 = 10.52
If the person doing laundry adds a base, such as the sodium silicate (Na4SiO4) in some detergents, to the wash water until the pH is raised to 10.52, the manganese ion will be reduced to a concentration of 1.8 × 10–6 M; at that concentration or less, the ion will not stain clothing.
Check Your Learning
The first step in the preparation of magnesium metal is the precipitation of Mg(OH)2 from sea water by the addition of Ca(OH)2. The concentration of Mg2+(aq) in sea water is 5.37 × 10–2 M. Calculate the pH at which [Mg2+] is diminished to 1.0 × 10–5 M by the addition of Ca(OH)2.
Answer:
11.13
Common Ion Effect
As we saw when we discussed buffer solutions, the hydronium ion concentration of an aqueous solution of acetic acid decreases when the strong electrolyte sodium acetate, NaCH3COO, is added. We can explain this effect using Le Châtelier’s principle. The addition of acetate ions causes the equilibrium to shift to the left, decreasing the concentration of H3O+ to compensate for the increased acetate ion concentration. This increases the concentration of CH3COOH:
CH3COOH(aq) + H2O(ℓ) ⇌ H3O+(aq) + CH3COO–(aq)
Because sodium acetate and acetic acid have the acetate ion in common, the influence on the equilibrium is called the common ion effect.
The common ion effect can also have a direct effect on solubility equilibria. Suppose we are looking at the reaction where silver iodide is dissolved:
AgI(s) ⇌ Ag+(aq) + I–(aq)
If we were to add potassium iodide (KI) to this solution, we would be adding a substance that shares a common ion with silver iodide. Le Châtelier’s principle tells us that when a change is made to a system at equilibrium, the reaction will shift to counteract that change. In this example, there would be an excess of iodide ions, so the reaction would shift toward the left, causing more silver iodide to precipitate out of solution.
Example 9
Common Ion Effect
Calculate the molar solubility of cadmium sulfide (CdS) in a 0.010-M solution of cadmium bromide (CdBr2). The Ksp of CdS is 1.0 × 10–28.
Solution
The first thing you should notice is that the cadmium sulfide is dissolved in a solution that contains cadmium ions. We need to use an ICE table to set up this problem and include the CdBr2 concentration as a contributor of cadmium ions:
CdS(s) ⇌ Cd2+(aq) + S2-(aq)
| CdS(s) ⇌ Cd2+(aq) + S2-(aq) | |||
| I: Initial concentration (M) | – | 0.010 | 0 |
| C: Change (M) | – | +x | +x |
| E: Equilibrium concentration (M) | – | 0.010 + x | x |
Ksp = [Cd2+][S2-] = 1.0 × 10-28
(0.010 + x)(x) = 1.0 × 10-28
x2 + 0.010x – (1.0 × 10-28) = 0
We can solve this equation using the quadratic formula, but we can also make an assumption to make this calculation much simpler. Since the Ksp value is so small compared with the cadmium concentration, we can assume that the change between the initial concentration and the equilibrium concentration is negligible, so that 0.010 + x ≈ 0.010. Going back to our Ksp expression, we would now get:
Ksp = [Cd2+][S2-] = 1.0 × 10-28
(0.010)(x) = 1.0 × 10-28
x = 1.0 × 10-26
Therefore, the molar solubility of CdS in this solution is 1.0 × 10–26 M.
Check Your Learning
Calculate the molar solubility of aluminum hydroxide, Al(OH)3, in a 0.015 M solution of aluminum nitrate, Al(NO3)3. The Ksp of Al(OH)3 is 1.3 × 10–33.
Answer:
1.5 × 10–11 M
Dissolution versus Weak Electrolyte Formation
We can determine how to shift the concentration of ions in the equilibrium between a slightly soluble solid and a solution of its ions by applying Le Châtelier’s principle. For example, one way to control the concentration of manganese(II) ion, Mn2+, in a solution is to adjust the pH of the solution and, consequently, to manipulate the equilibrium between the slightly soluble solid manganese(II) hydroxide, manganese(II) ion, and hydroxide ion:
Mn(OH)2(s) ⇌ Mn2+(aq) + 2 OH–(aq) Ksp = [Mn2+][OH–]2
This could be important to a laundry because clothing washed in water that has a manganese concentration exceeding 0.1 mg per liter may be stained by the manganese. We can reduce the concentration of manganese by increasing the concentration of hydroxide ion. We could add, for example, a small amount of NaOH or some other base such as the silicates found in many laundry detergents. As the concentration of OH– ion increases, the equilibrium responds by shifting to the left and reducing the concentration of Mn2+ ion while increasing the amount of solid Mn(OH)2 in the equilibrium mixture, as predicted by Le Châtelier’s principle.
Example 10
Solubility Equilibrium of a Slightly Soluble Solid
What is the effect on the amount of solid Mg(OH)2 that dissolves and the concentrations of Mg2+ and OH– when each of the following are added to a mixture of solid Mg(OH)2 in water at equilibrium?
- MgCl2
- KOH
- an acid
- NaNO3
- Mg(OH)2
Solution
The equilibrium among solid Mg(OH)2 and a solution of Mg2+ and OH– is:
Mg(OH)2(s) ⇌ Mg2+(aq) + 2 OH–(aq)
(a) The reaction shifts to the left to relieve the stress produced by the additional Mg2+ ion, in accordance with Le Châtelier’s principle. In quantitative terms, the added Mg2+ causes the reaction quotient to be larger than the solubility product (Q > Ksp), and Mg(OH)2 forms until the reaction quotient again equals Ksp. At the new equilibrium, [OH–] is less and [Mg2+] is greater than in the solution of Mg(OH)2 in pure water. More solid Mg(OH)2 is present.
(b) The reaction shifts to the left to relieve the stress of the additional OH– ion. Mg(OH)2 forms until the reaction quotient again equals Ksp. At the new equilibrium, [OH–] is greater and [Mg2+] is less than in the solution of Mg(OH)2 in pure water. More solid Mg(OH)2 is present.
(c) The concentration of OH– is reduced as the OH– reacts with the acid. The reaction shifts to the right to relieve the stress of less OH– ion. In quantitative terms, the decrease in the OH– concentration causes the reaction quotient to be smaller than the solubility product (Q < Ksp), and additional Mg(OH)2 dissolves until the reaction quotient again equals Ksp. At the new equilibrium, [OH–] is less and [Mg2+] is greater than in the solution of Mg(OH)2 in pure water. More Mg(OH)2 is dissolved.
(d) NaNO3 contains none of the species involved in the equilibrium, so we should expect that it has no appreciable effect on the concentrations of Mg2+ and OH–. (As we have seen previously, dissolved salts change the activities of the ions of an electrolyte. However, the salt effect is generally small, and we shall neglect the slight errors that may result from it.)
(e) The addition of solid Mg(OH)2 has no effect on the solubility of Mg(OH)2 or on the concentration of Mg2+ and OH–. The concentration of Mg(OH)2 does not appear in the equation for the reaction quotient:
Thus, changing the amount of solid magnesium hydroxide in the mixture has no effect on the value of Q, and no shift is required to restore Q to the value of the equilibrium constant.
Check Your Learning
What is the effect on the amount of solid NiCO3 that dissolves and the concentrations of Ni2+ and CO32- when each of the following are added to a mixture of the slightly soluble solid NiCO3 and water at equilibrium?
- Ni(NO3)2
- KClO4
- NiCO3
- K2CO3
- HNO3 (reacts with carbonate giving HCO3– or H2O and CO2)
Answer:
- mass of NiCO3(s) increases, [Ni2+] increases, [CO32-] decreases;
- no appreciable effect;
- no effect except to increase the amount of solid NiCO3;
- mass of NiCO3(s) increases, [Ni2+] decreases, [CO32-] increases;
- mass of NiCO3(s) decreases, [Ni2+] increases, [CO32-] decreases
Key Concepts and Summary
Although the solubility rules often taught in general chemistry identify solids as either 100% soluble or 100% insoluble, even insoluble solids dissociate to small degree in solution. Using a reaction (solid ⇌ aqueous) and Ksp, we can calculate the extent that any solid dissociates in solution, resulting in its molar solibility, or the moles of solid that dissolve in 1 L of water.
The reaction quotient, Q, can also be used to predict whether precpitation or dissolution occurs at certain conditions. When Q equals Ksp, the system is at equilibrium; if Q is less than Ksp, the solid will dissolve until Q equals Ksp; if Q is greater than Ksp, precipitation will occur at a given temperature until Q equals Ksp.
If a solid is added to a solution that contains one of the solid’s dissociative ions, the common ion effect dictates that the solubility of the solid decreases. If the solid is added to a solution that reacts with one of the solid’s dissociative ions, the solubility of the solid increases.
Glossary
- common ion effect
- the influence on an equilibrium when a solid’s dissociation results in a common ion already present in the solution
- molar solubility
- a solid’s solubility expressed in units of moles per liter (mol/L)
- solubility product (Ksp)
- the equilibrium constant for the equilibrium between a slightly soluble ionic solid and a solution of its ions
Chemistry End of Section Exercises
- Complete the changes in concentrations for each of the following reactions (fill in the ___):
(a) AgI(s) ⇌ Ag+(aq) + I–(aq) +x ___ (b) Mg(OH)2(s) ⇌ Mg2+(aq) + 2 OH–(aq) +x ___ (c) Ag2SO4(s) ⇌ 2 Ag+(aq) + SO42-(aq) ___ ___ - When solving for the solubility of Mg(OH)2, what algebraic equation, involving Mg(OH)2 Ksp, would need to be solved?
- x2 = Ksp
- 2x2 = Ksp
- x3 = Ksp
- 2x3 = Ksp
- 4x3 = Ksp
- How do the concentrations of Ag+ and CrO42- in a saturated solution above 1.0 g of solid Ag2CrO4 change when 100 g of solid Ag2CrO4 is added to the system? Explain.
- What additional information do we need to answer the following question: How is the equilibrium of solid silver bromide with a saturated solution of its ions affected when the temperature is raised?
- Write the solubility product (Ksp) expression for each of the following slightly soluble ionic compounds:
- PbCl2
- Sr3(PO4)2
- SrSO4
- The Handbook of Chemistry and Physics gives solubilities of the following compounds in grams per 100 mL of water. Because these compounds are only slightly soluble, assume that the volume does not change on dissolution and calculate the solubility product for each.
- BaSeO4: 0.0118 g/100 mL
- Ba(BrO3)2·H2O: 0.30 g/100 mL
- La2(MoO4)3: 0.00179 g/100 mL
- A saturated solution of CaF2 is has a concentration of Ca2+ of 1.1 × 10-3 M and a concentration of F– of 2.2 × 10-3 M. What is the solubility product of CaF2?
- The solubility of PbI2 is 0.064 g/100 mL at 20 °C. What is the solubility product, Ksp, for PbI2? The molar mass of PbI2 is 461.0 g/mol.
- Calculate the concentration of all solutes that result when excess Pb(IO3)2 is dissolved at 25°C. (Ksp Pb(IO3)2 = 1.2 × 10-13)
- The Ksp value for Bi2S3 is 1.9 × 10-31.
- What is the molar solubility of the compound?
- What is the concentration of Bi3+ ions in a saturated solution of Bi2S3(aq)?
- Assuming that no equilibria other than dissolution are involved, calculate the concentration of all solute species in each of the following solutions of salts in contact with a solution containing a common ion.
- AuCl(s) in 0.025 M AuNO3 (Ksp AuCl = 2.0 × 10-13)
- Hg2Cl2(s) in 0.0313 M KCl (Ksp Hg2Cl2 = 1.3 × 10-18) Hint: Mercury I is Hg22+.
- MgC2O4 in 2.250 L of a solution containing 8.156 g of Mg(NO3)2 (Ksp MgC2O4 = 4.83 × 10-6)
- Perform the following calculations:
- Calculate [Ag+] in a saturated aqueous solution of AgBr. (Ksp AgBr = 5.0 × 10-13)
- What will [Ag+] be when enough KBr(s) has been added to make Br– concentration at equilibrium 0.050 M? Assume no volume change.
- The solubility product of CaSO4 is 9.1 × 10–6. What mass of this salt will dissolve in 1.0 L of 0.010 M SO42−?
- How many grams of Pb(OH)2 will dissolve in 500 mL of a 0.050-M PbCl2 solution (Ksp = 1.2 × 10–15)?
- Calculate the molar solubility of CaF2 in a 0.25 M NaF solution. Ksp(CaF2) = 4.0 × 10-11.
- Calculate the molar solubility of iron(II) hydroxide, Fe(OH)2, in a solution buffered at a pH of 13.15. The Ksp of Fe(OH)2 is 1.6 × 10-14.
- For PbCl2 (Ksp = 2.4 × 10-4), will a precipitate of PbCl2 form when 0.10 L of 3.0 × 10-2 M Pb(NO3)2 is added to 400.0 mL of 9.0 × 10-2 M NaCl?
- Yes, because Q > Ksp
- No, because Q < Ksp
- No, because Q = Ksp
- Yes, because Q < Ksp
- Yes, because Q = Ksp
- Which of the following would decrease the Ksp for PbI2?
- Lowering the pH of the solution.
- Adding a solution of Pb(NO3)2.
- Adding a solution of KI.
- All of the above.
- None of the above.
- Which of the following compounds is more soluble in an acidic solution than in pure water? Select all that apply.
- FeS
- BaCO3
- CuI
- PbCl2
- NH4NO3
- Silver carbonate, Ag2CO3, is a sparingly soluble compound with Ksp = 8.1 × 10-12.
- Determine the molar solubility of this compound in water.
- Indicate whether the solubility of Ag2CO3 (determined in g/L) would be higher, lower, or the same in the following scenarios. Justify your answer each time.
- The solubility of Ag2CO3 (determined in g/L) in 1.00 L of 0.10 M Na2CO3(aq) solution compared to 1.00 L of pure water.
- The solubility of Ag2CO3 (determined in g/L) in 1.00 L of a 0.10 M AgNO3(aq) solution compared to 1.00 L of pure water.
- The solubility of Ag2CO3 (determined in g/L) in 1.00 L of a solution at pH = 2.00 compared to 1.00 L of pure water.
- The solubility of Ag2CO3 (determined in g/L) in 2.00 L of water compared to 1.00 L of water.
Answers to Chemistry End of Section Exercises
-
(a) AgI(s) ⇌ Ag+(aq) + I–(aq) +x +x (b) Mg(OH)2(s) ⇌ Mg2+(aq) + 2 OH–(aq) +x +2x (c) Ag2SO4(s) ⇌ 2 Ag+(aq) + SO42-(aq) +2x +x - E
- Neither concentration will change. The solution is saturated and already has as much dissolved as possible at that temperature.
- The solubility of silver bromide at the new temperature must be known. Normally the solubility increases and some of the solid silver bromide will dissolve.
- (a) [Pb2+][Cl–]2
(b) [Sr2+]3[PO42-]2
(c) [Sr2+][SO42-] - (a) 1.77 × 10–7; (b) 1.6 × 10–6; (c) 7.91 × 10–22
- 5.3 × 10-9
- 1.1 × 10-8
- [Pb2+] = 3.1 × 10-5; [IO3–] = 6.2 × 10-5
- (a) 2.8 × 10-7 M; (b) 5.6 × 10-7 M
- (a) [Au+] = 0.025 M, [Cl–] = 8.0 × 10-12 M
(b) [Hg22+] = 1.3 × 10-15 M, [Cl–] = 0.0313 M
(c) [Mg2+] = 0.0244 M, [C2O42-] = 1.98 × 10-4 M - (a) 7.1 × 10-7 M; (b) 1.0 × 10-11 M
- 0.12 grams
- 1.8 × 10–5 g Pb(OH)2
- 6.4 × 10-10 M
- 8.0 × 10-13 M
- B
- E
- A and B.
- (a) 1.3 × 10–4 M
(b) (i) Lower Solubility. The common ion effect predicts that the common ion (CO32-) reduces the solubility of Ag2CO3.
(ii) Lower Solubility. The common ion effect predicts that the common ion (Ag+) reduces the solubility of Ag2CO3.
(iii) Higher Solubility. When Ag2CO3 dissociates in solution, CO32- readily picks up H+ ions to form HCO3–, which shifts the equilibrium towards making more CO32-.
(iv) Same Solubility. Solubility is affected by many factors (such as temperature and the presence of common ions) but it is not affected by increasing the amount of solvent.
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

