M6Q2: Direction of Heat Flow and System vs. Surroundings
Introduction
The section explores heat as a form of energy and the direction of heat flow. We will apply these concepts to chemical reactions. This section includes sample problems, key equations, and a glossary.
Learning Objectives for Direction of Heat Flow and System vs Surroundings
- Explain and illustrate the connection between temperature, heat, and direction of heat flow.
| Thermal Energy | Temperature | Heat | - Distinguish between the system and the surroundings.
| System vs. Surroundings |
| Key Concepts and Summary | Key Equations | Glossary | End of Section Exercises |
Thermal Energy, Temperature, and Heat
Knowledge of thermodynamic principles is essential for understanding chemistry, and indeed, all scientific disciplines. It is one thing to be able to predict the products of a precipitation reaction by applying solubility rules, for example, but to understand why the reaction occurs at a more fundamental level requires insight into the energy changes of the process. In fact when answering a question in chemistry that begins with the word “why”, the answer will likely require a thermodynamic explanation. The laws of thermodynamics are fundamental to natural science. Our lives are governed by these laws, but there is no penalty for breaking them, because as far as we know they cannot be broken.
The phrases thermal energy, temperature, and heat are often used interchangeably and incorrectly. To a chemist, these concepts have very different meanings. To illustrate the difference, we’ll examine the thermal energy, temperature, and heat associated with 1.0 g of water at 50 °C and 100.0 g of water at 50 °C.
Thermal Energy
Thermal energy is the kinetic energy associated with the random motion of atoms and molecules. This molecular motion can include translation (directional movement), rotation (tumbling), and vibration (stretching and flexing along the bond axis between two atoms in a molecule), shown in Figure 1. Thermal energy is an extensive property, meaning that the amount of the substance matters. Referring to our water example, the 1.0 g of water at 50 °C has 100 times less thermal energy than the 100.0 g of water at 50 °C because there are fewer molecules in motion in the smaller sample.
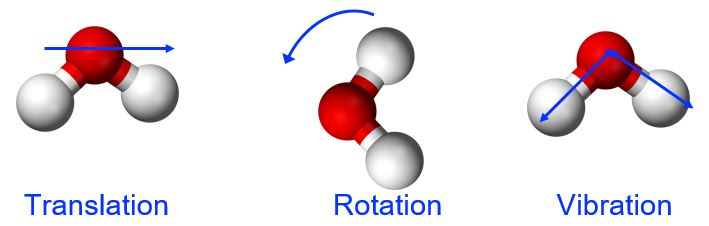
Temperature
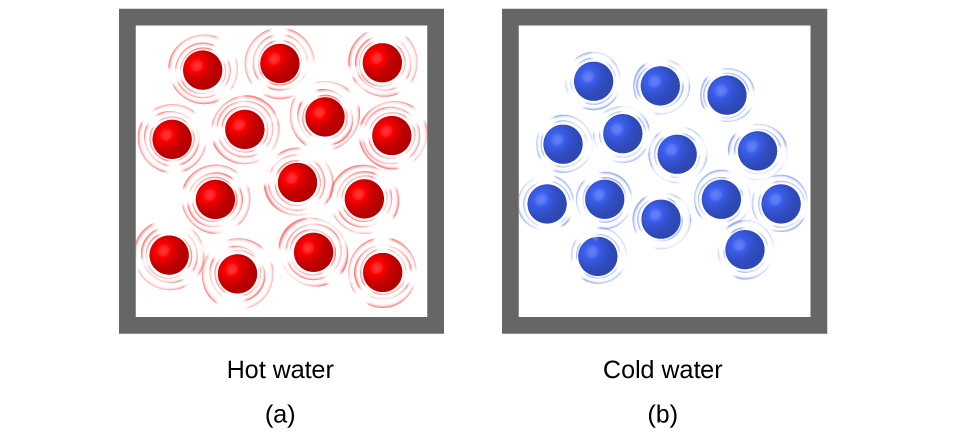
Temperature is a quantitative measure of “hot” or “cold.” Recall from the previous module that temperature is a measure of the average translational kinetic energy per molecule in a gas, liquid, or solid. Referring to our water example, the 1.0 g of water at 50 °C has the same temperature as the 100.0 g of water at 50 °C, even though the thermal kinetic energy is 100 times greater in the 100.0 sample of water. Temperature is an intensive property, meaning that the amount of the substances does not matter.
When the atoms and molecules in an object are moving or vibrating quickly, they have a higher average kinetic energy (KE), and we say that the object is “hot.” When the atoms and molecules are moving slowly, they have lower average KE, and we say that the object is “cold” (Figure 2). Assuming that no chemical reaction or physical change occurs, increasing the amount of thermal energy in a sample of matter will cause its temperature to increase because the average KE of the sample increases. And, assuming that no chemical reaction or physical change occurs, decreasing the amount of thermal energy in a sample of matter will cause its temperature to decrease. Temperature is thus a measure of the average translational KE of the particles in a sample.

Click on this interactive simulation to view the effects of temperature on molecular motion.
Heat
Heat (q) is the transfer of thermal energy between two substances at different temperatures. Referring to our water example, we cannot talk about the heat of the 1.0 g of water at 50 °C or the heat of the 100.0 g of water at 50 °C. Heat requires a flow of energy and results in a change in temperature; these examples are both stable at 50 °C. Even though the 100.0 g sample of water at 50 °C has a higher thermal energy than the 1.0 g sample of water at 50 °C, since there is not a temperature difference between the samples, no heat will flow.
Heat flow (a redundant term, but one commonly used) increases the thermal energy of one substance and decreases the thermal energy of the other (Figure 3). Suppose we initially have a high temperature (and high thermal energy) substance (H) and a low temperature (and low thermal energy) substance (L). The atoms and molecules in H have a higher average KE than those in L. If we place substance H in contact with substance L, the thermal energy will flow spontaneously from substance H to substance L. The temperature of substance H will decrease, as will the average KE of its molecules; the temperature of substance L will increase, along with the average KE of its molecules. Heat flow will continue until the two substances are at the same temperature (Figure 3).
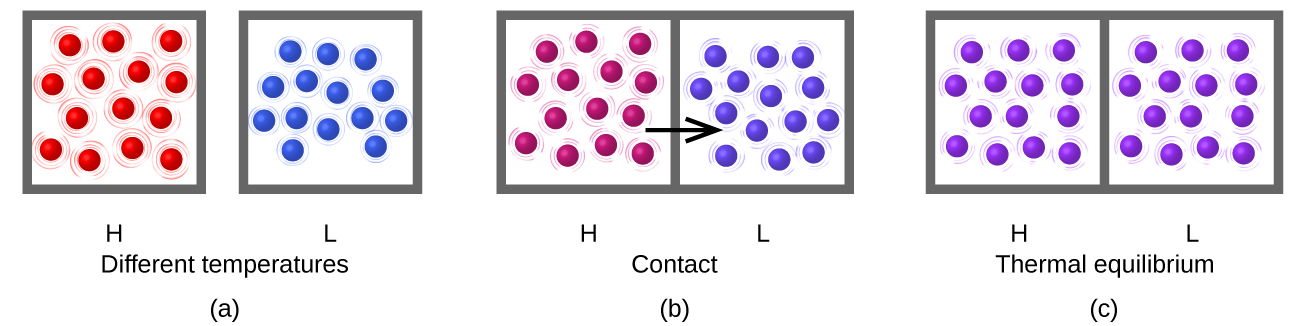
What is the mechanism of this energy transfer that we call heat? Energy is transferred through myriad random collisions of the hot molecules (red) with the walls of the container (gray box, e.g. iron), whose own atoms vibrate and collide with the molecules of the cold gas (blue). These collisions transfer energy from the hot molecules to the cold molecules because the hotter molecules move faster than colder ones (if they have the same mass), and thereby speed them up when they collide. The hotter molecules cool down (lower average kinetic energy per molecule and therefore lower temperature) and the colder molecules warm up (higher average kinetic energy per molecule and therefore higher temperature). No more energy is transferred (no heat flows) when the blue and red molecules have the same temperature and therefore the same average kinetic energy per molecule!
System vs. Surroundings
The measurement of heat transfer requires the definition of a system (the substance or substances undergoing the chemical or physical change) and its surroundings (everything else in contact with the system). Together, the system and surroundings constitute the universe from a thermodynamic perspective. Although there is heat transferred between the system and surroundings, there is no heat transferred into or out of the universe and quniverse is zero.
quniverse = 0 = qsystem + qsurroundings
We can rearrange this equation to state that:
qsystem = –qsurroundings
This relation just says that the energy that flows out of or into the system must exactly balance the energy that flow into or out of the surroundings. They must sum to zero. For example, if we measure the heat change in the water surrounding a chemical reaction, then we know the heat change in the chemical reaction is equal in magnitude and opposite in sign. Note that in this example the system can be the reactants and products dissolved in water, while the surroundings are the water itself. This is the common case for coffee-cup calorimetry that will be discussed in a later section.
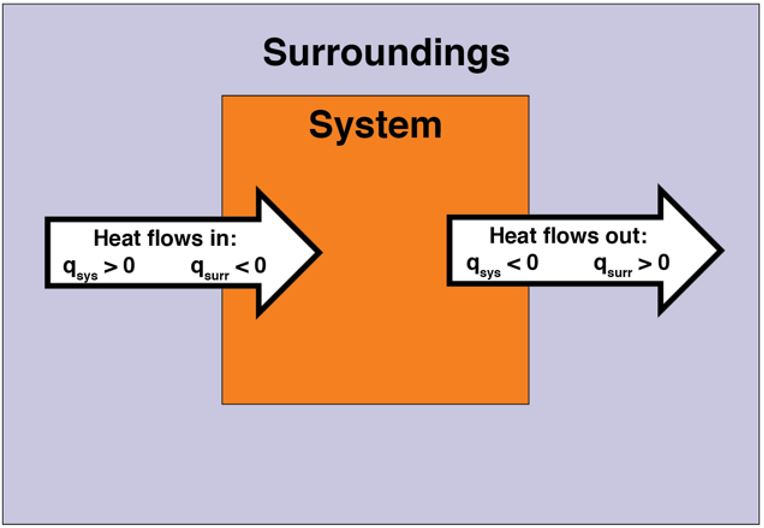
In the previous section, we discussed endothermic and exothermic chemical reactions (and physical processes). In an endothermic reaction, energy flows into the system. Thus, heat is positive (q > 0) from the point of view of the system. Heat is transferred from the surroundings into the system. In contrast, in an exothermic reaction, energy flows out of the system. Thus, heat is negative (q < 0) from the point of view of the system. Heat is transferred from the system into the surroundings. Figure 4 illustrates heat flow.
Example 1
Determine the direction of heat flow
When frost hits fruit growers at crucial periods, farmers spray mist on their crops to keep them from cooling to the air temperature. Determine the direction of heat flow when liquid water freezes to form solid water:
H2O(ℓ) ⟶ H2O(s)

Solution
As water freezes, bonds are made between water molecules and the physical change is exothermic; heat flows from the system to the surroundings. Here, the system is the water on the surface of the fruit and the surroundings includes the fruit. Heat flows from the water to the fruit, keeping the fruit from cooling to the air temperature which can be much lower than the ) 0 °C temperature at which pure water freezes.
Check Your Learning
Determine the direction of heat flow when hydrogen gas is ignited in the presence of oxygen gas to from water vapor.
2 H2(g) + O2(g) ⟶ 2 H2O(g)
Watch the demonstration here (start video playback around 1:10):
Answer:
This is an exothermic chemical reaction; heat flows from the system to the surroundings. Here, the system includes everything inside the balloon and the surroundings includes everything outside the balloon. The flame is necessary to start the reaction, but it is ignored when discussing the heat flow.
Key Concepts and Summary
Matter has thermal energy (extensive property) due to the kinetic energy of its molecules. The temperature (intensive property) of this matter is equal to the average kinetic energy per molecule. Heat is energy that is transferred between objects at different temperatures: energy flows from high temperature to low temperature by myriad random collisions between the molecules or atoms of the two objects.
Key Equations
- quniverse = 0 = qsystem + qsurroundings
- qsystem = –qsurroundings
Glossary
- heat (q)
- transfer of thermal energy between two substances
- surroundings
- all matter other than the system being studied
- system
- portion of matter undergoing a chemical or physical change being studied
- temperature
- intensive property of matter that is a quantitative measure of “hotness” and “coldness”
- thermal energy
- kinetic energy associated with the random motion of atoms and molecules
Chemistry End of Section Exercises
- A 500-mL bottle of water at room temperature and a 2-L bottle of water at the same temperature were placed in a refrigerator. After 30 minutes, the 500-mL bottle of water had cooled to the temperature of the refrigerator. An hour later, the 2-L of water had cooled to the same temperature. When asked which sample of water lost the most heat, one student replied that both bottles lost the same amount of heat because they started at the same temperature and finished at the same temperature. A second student thought that the 2-L bottle of water lost more heat because there was more water. A third student believed that the 500-mL bottle of water lost more heat because it cooled more quickly. A fourth student thought that it was not possible to tell because we do not know the initial temperature and the final temperature of the water. Indicate which of these answers is correct and describe the error in each of the other answers.
- When 50.0 mL of 0.10 M HCl(aq) and 50.0 mL of 0.10 M NaOH(aq), both at 22.0 °C, are added to a coffee cup calorimeter, the temperature of the mixture reaches a maximum of 28.9 °C degrees. Would the amount of heat measured for this reaction be greater, lesser, or remain the same if we used a calorimeter that was a poorer insulator than a coffee cup calorimeter? Explain your answer.
- When solid ammonium nitrate dissolves in water, the solution becomes cold. This is the basis for an “instant ice pack”. When 3.21 g of solid NH4NO3 dissolves in 50.0 g of water at 24.9 °C in a calorimeter, the temperature decreases to 20.3 °C. Would the amount of heat absorbed by the dissolution appear greater, lesser, or remain the same if the experimenter used a calorimeter that was a poorer insulator than a coffee cup calorimeter? Explain your answer.
- True or False: In the reaction: H+(aq) + OH–(aq) → H2O(ℓ), heat flow for the system is negative.
Answers to Chemistry End of Section Exercises
- The second student was correct. The error that the first student made is that he ignored the mass of water. For the third student, it should be 2L bottle of water lost more heat since it takes longer time to reach the temperature of the fridge. The mistake the fourth student make is that even though we do not know the initial T and the final T, we could still answer this question; because the ΔT are the same in two systems and it would not affect the comparison.
- Lesser; more heat would be lost to the coffee cup and the environment and so ΔT for the water would be lesser and the calculated q would be lesser.
- Lesser; heat from the environment would make ΔT smaller since the heat can affect the temperature of the reaction system, and the calculated q would be lesser.
- True
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

