M7Q5: DeBroglie, Intro to Quantum Mechanics, Quantum Numbers 1-3

Introduction

Bohr’s model explained the experimental data for the hydrogen atom and was widely accepted, but it also raised many questions. Why did electrons orbit at only fixed distances defined by a single quantum number n = 1, 2, 3, and so on, but never in between? Why did the model work so well describing hydrogen and one-electron ions, but could not correctly predict the emission spectrum for helium or any larger atoms? The goal of this section is to answer these questions by introducing electron orbitals, their different energies, and other properties. This section includes worked examples, sample problems, and a glossary.

Learning Objectives for DeBroglie, Intro to Quantum Mechanics, Quantum Numbers 1-3

| Key Concepts and Summary | Glossary | End of Section Exercises |

Behavior in the Microscopic World and De Broglie Wavelength

We know how matter behaves in the macroscopic world—objects that are large enough to be seen by the naked eye follow the rules of classical physics. A billiard ball moving on a table will behave like a particle: It will continue in a straight line unless it collides with another ball or the table cushion, or is acted on by some other force (such as friction). The ball has a well-defined position and velocity (or a well-defined momentum, p = mv, defined by mass m and velocity v) at any given moment. In other words, the ball is moving in a classical trajectory. This is the typical behavior of a classical object.

One of the first people to pay attention to the special behavior of the microscopic world was Louis de Broglie. He asked the question: If electromagnetic radiation can have particle-like character (as we saw in an earlier section), can electrons and other submicroscopic particles exhibit wavelike character? In his 1925 doctoral dissertation, de Broglie extended the wave–particle duality of light that Einstein used to resolve the photoelectric effect paradox to material particles. He predicted that a particle with mass m and velocity v (that is, with linear momentum p) should also exhibit the behavior of a wave with a wavelength value λ, given by this expression in which h is the familiar Planck’s constant:

λ = \dfrac{h}{mv} = \dfrac{h}{p}

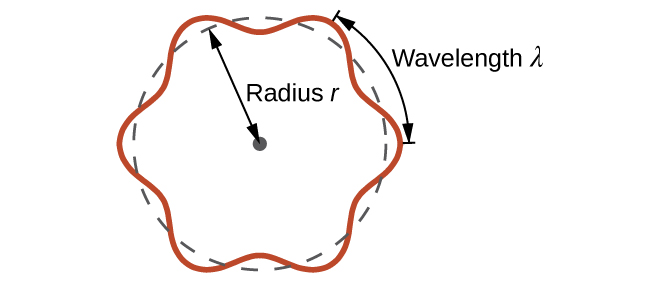
This quantity is called the de Broglie wavelength. Unlike the other values of λ discussed in this chapter, the de Broglie wavelength is a characteristic of particles and other bodies, not electromagnetic radiation (note that this equation involves velocity [v, with units m/s], not frequency [ν, with units Hz]. Although these two symbols are similar, they mean very different things). Where Bohr had postulated the electron as being a particle orbiting the nucleus in quantized orbits, de Broglie argued that Bohr’s assumption of quantization can be explained if the electron is considered not as a particle, but rather as a circular standing wave such that only an integer number of wavelengths could fit exactly within the orbit (Figure 1).

This figure includes a circle formed from a dashed line. A sinusoidal wave pattern indicated with a solid red line is wrapped around the circle, centered about the edge of the circle. Line segments extend outward from the circle extending through 2 wave crests along the circle. A double ended arrow is drawn between these segments and is labeled, “wavelength, lambda.” A dashed double headed arrow is drawn from the center to the edge of the circle and is labeled, “radius r.”
Figure 1. If an electron is viewed as a standing wave circling around the nucleus, an integer number of wavelengths must fit into the orbit for this standing wave behavior to be possible.

Interference Patterns are a Hallmark of Wavelike Behavior

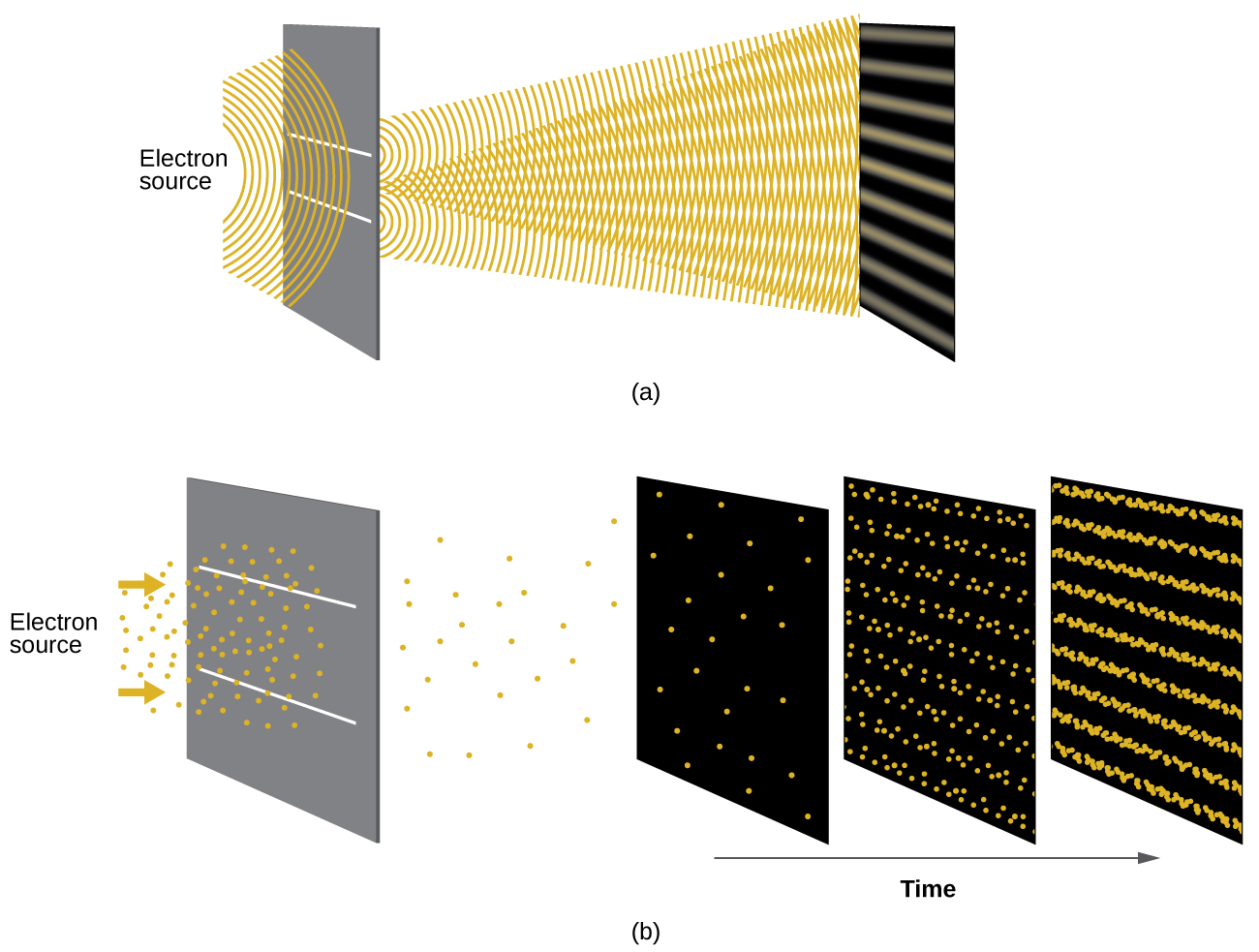
Shortly after de Broglie proposed the wave nature of matter, two scientists at Bell Laboratories, C. J. Davisson and L. H. Germer, demonstrated experimentally that electrons can exhibit wavelike behavior by showing an interference pattern for electrons reflecting off a crystal. The same interference pattern is also observed when electrons travel through a regular atomic pattern in a crystal. The regularly spaced atomic layers served as slits that diffract the electrons, as used in other interference experiments. Since the spacing between the layers serving as slits needs to be similar in size to the wavelength of the tested wave for an interference pattern to form, Davisson and Germer used a crystalline nickel target for their “slits,” since the spacing of the atoms within the lattice was approximately the same as the de Broglie wavelengths of the electrons that they used. Figure 2 shows an interference pattern. The wave–particle duality of matter can be seen in Figure 2 by observing what happens if electron collisions are recorded over a long period of time. Initially, when only a few electrons have been recorded, they show clear particle-like behavior, having arrived in small localized packets that appear to be random. As more and more electrons arrived and were recorded, a clear interference pattern that is the hallmark of wavelike behavior emerged. Thus, it appears that while electrons are small localized particles, their motion does not follow the equations of motion implied by classical mechanics, but instead it is governed by some type of a wave equation that governs a probability distribution even for a single electron’s motion. Thus the wave–particle duality first observed with photons is actually a fundamental behavior intrinsic to all quantum particles.

This figure has two parts. Part a shows a diagram of an electron source emitting waves that pass through two narrow slits in a barrier. A wave interference pattern results on the opposite side of the barrier that result in evenly spaced, relatively wide horizontal grey lines on a black surface. The black surface is placed at a distance beyond the barrier. Part b shows an electron source at the far left. Two gold arrows point toward two narrow horizontal slits in a barrier. Around these arrows are many small golden dots. On the right side of the barrier, the gold dots are more widely dispersed. A black surface a distance beyond the barrier shows evenly, yet widely dispersed gold dots. An arrow is present below this black surface and is labeled, “Time.” A second black surface is shown to the right that has many more golden dots that appear to be organizing into a pattern of evenly spaced horizontal line segments. A third black surface is shown even further to the right in which many more gold dots are shown in a very clearly established, evenly spaced pattern of horizontal line segments.
Figure 2. (a) The interference pattern for electrons passing through very closely spaced slits demonstrates that quantum particles such as electrons can exhibit wavelike behavior. (b) The experimental results illustrated here demonstrate the wave–particle duality in electrons. The electrons pass through very closely spaced slits, forming an interference pattern, with increasing numbers of electrons being recorded from the left image to the right. With only a few electrons recorded, it is clear that the electrons arrive as individual localized “particles,” but in a seemingly random pattern. As more electrons arrive, a wavelike interference pattern begins to emerge. Note that the probability of the final electron location is still governed by the wave-type distribution, even for a single electron, but it can be observed more easily if many electron collisions have been recorded.

 

View the Dr. Quantum – Double Slit Experiment cartoon for an easy-to-understand description of wave–particle duality and the associated experiments.

Chemistry in Real Life: Dorothy Hodgkin

Because the wavelengths of X-rays (10-10,000 picometers [pm]) are comparable to the size of atoms, X-rays can be used to determine the structure of molecules. When a beam of X-rays is passed through molecules packed together in a crystal, the X-rays collide with the electrons and scatter. Constructive and destructive interference of these scattered X-rays creates a specific diffraction pattern. Calculating backward from this pattern, the positions of each of the atoms in the molecule can be determined very precisely. One of the pioneers who helped create this technology was Dorothy Crowfoot Hodgkin.

She was born in Cairo, Egypt, in 1910, where her British parents were studying archeology. Even as a young girl, she was fascinated with minerals and crystals. When she was a student at Oxford University, she began researching how X-ray crystallography could be used to determine the structure of biomolecules. She invented new techniques that allowed her and her students to determine the structures of vitamin B12, penicillin, and many other important molecules. Diabetes, a disease that affects 382 million people worldwide, involves the hormone insulin. Hodgkin began studying the structure of insulin in 1934, but it required several decades of advances in the field before she finally reported the structure in 1969. Understanding the structure has led to better understanding of the disease and treatment options.

Example 1

Calculating the Wavelength of a Particle
If an electron travels at a velocity of 1.000 × 107 m/s and has a mass of 9.109 × 10–28 g, what is its wavelength?

Solution
We can use de Broglie’s equation to solve this problem, but we first must do a unit conversion of Planck’s constant. You learned earlier that 1 J = 1 kg·m2/s2. Thus, we can write h = 6.626 × 10–34 J·s as 6.626 × 10–34 kg·m2/s.

λ = 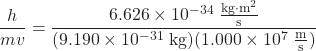\dfrac{h}{mv} = \dfrac{6.626 \times 10^{-34}\;\frac{\text{kg}{\cdot}\text{m}^{2}}{\text{s}}}{(9.190 \times 10^{-31} \;\text{kg})(1.000 \times 10^{7}\;\frac{\text{m}}{\text{s}})} = 7.274 × 10-11 m

This is a small value, but it is significantly larger than the size of an electron in the classical (particle) view. This size is the same order of magnitude as the size of an atom. This means that electron wavelike behavior is going to be noticeable in an atom.

Check Your Learning
Calculate the wavelength of a softball with a mass of 100 g traveling at a velocity of 35 m/s, assuming that it can be modeled as a single particle.

Answer:

1.9 × 10–34 m

We never think of a thrown softball having a wavelength, since this wavelength is so small it is impossible for our senses or any known instrument to detect. The de Broglie wavelength is only appreciable for matter that has a very small mass and/or a very high velocity.

The Quantum–Mechanical Model of an Atom

Shortly after de Broglie published his ideas that the electron in a hydrogen atom could be better thought of as being a circular standing wave instead of a particle moving in quantized circular orbits, as Bohr had argued, Erwin Schrödinger extended de Broglie’s work by incorporating the de Broglie relation into a wave equation, deriving what is today known as the Schrödinger equation. When Schrödinger applied his equation to hydrogen-like atoms, he was able to reproduce Bohr’s expression for the energy and, thus, the Rydberg formula governing hydrogen spectra. He did so without having to invoke Bohr’s assumptions of stationary states and quantized orbits, angular momenta, and energies. Quantization in Schrödinger’s theory was a natural consequence of the underlying mathematics of the wave equation. Like de Broglie, Schrödinger initially viewed the electron in hydrogen as being a physical wave instead of a particle, but where de Broglie thought of the electron in terms of circular stationary waves, Schrödinger properly thought in terms of three-dimensional stationary waves, or wavefunctions, represented by the Greek letter psi, ψ. A few years later, Max Born proposed an interpretation of the wavefunction, ψ, that is still accepted today: Electrons are still particles, and so the waves represented by ψ are not physical waves. However,  when you square them, you obtain the probability density which  describes the probability of the quantum particle being present near a certain location in space. Wavefunctions, therefore, can be used to determine the distribution of the electron’s density with respect to the nucleus in an atom, but cannot be used to pinpoint the exact location of the electron at any given time. In other words, they predict the energy levels available for electrons in an atom and the probability of finding an electron at a particular place in an atom. Schrödinger’s work, as well as that of Heisenberg and many other scientists following in their footsteps, is generally referred to as quantum mechanics.

 

You may also have heard of Schrödinger because of his famous thought experiment. This story explains the concepts of superposition and entanglement as related to a cat in a box with poison.

Understanding Quantum Theory of Electrons in Atoms

As was described previously, electrons in atoms can exist only on discrete energy levels but not between them. It is said that the energy of an electron in an atom is quantized, meaning it can be equal only to certain specific values. The electron can jump from one energy level to another, but it cannot transition smoothly because it cannot exist between the levels.

Principal Quantum Number

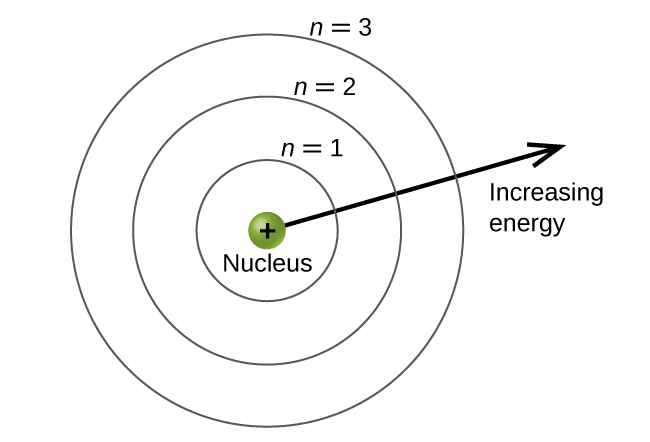
The energy levels are labeled with an n value, where n = 1, 2, 3, …, ∞. Generally speaking, the energy of an electron in an atom is greater for greater values of n. This number, n, is referred to as the principal quantum number. The principal quantum number defines the location of the energy level. It is essentially the same concept as the n in the Bohr atom description. Another name for the principal quantum number is the shell number. The shells of an atom can be thought of as concentric circles radiating out from the nucleus. The electrons that belong to a specific shell are most likely to be found within the corresponding circular area (not traveling along the circular ring like a planet orbiting the sun). The further we proceed from the nucleus, the higher the shell number, and so the higher the energy level (Figure 4). The positively charged protons in the nucleus stabilize the electronic orbitals by electrostatic attraction between the positive charges of the protons and the negative charges of the electrons. So the further away the electron is from the nucleus, the greater the energy it has.

This figure contains a central green sphere labeled “nucleus.” There is a plus sign in the middle of the sphere. This sphere is encircled by 3 concentric, evenly spaced rings. The first and closest to the center is labeled, “n equals 1.” The second ring is labeled, “n equals 2,” and the third ring is labeled, “n equals 3.” An arrow is drawn from the edge of the central sphere to the right extending out of the concentric rings. It is labeled, “increasing energy.”
Figure 4. Different shells are numbered by principal quantum numbers.

In a major advance over the Bohr theory of the hydrogen atom, in the quantum mechanical model, one can calculate the quantized energies of any isolated atom.  Knowing these energies one can then predict the frequencies and energies of photons that are emitted or absorbed based on the difference of the calculated energy levels using the equation presented in the previous quantum,   |ΔE| = |Ef − Ei| = hν.  In the case of the hydrogen atom, the expression simplifies to the previously obtained Bohr result.

ΔE = Efinal – Einitial = -2.179 × 10-18 \left(\dfrac{1}{n^2_\text{f}} - \dfrac{1}{n^2_\text{i}}\right) J

The principal quantum number is one of three quantum numbers used to characterize an orbital. An atomic orbital, which is distinct from an orbit, is a general region in an atom within which an electron is most probable to reside. More precisely, the orbital specifies the probability of finding an electron in the three-dimensional space around the nucleus and is based on solutions of the Schrödinger equation. In addition, the principal quantum number defines the energy of an electron in a hydrogen or hydrogen-like atom or an ion (an atom or an ion with only one electron) and the general region in which discrete energy levels of electrons in multi-electron atoms and ions are located.

Angular Momentum Quantum Number

Another quantum number is l, the angular momentum quantum number (this is sometimes referred to as the azimuthal quantum number). It is an integer that defines the shape of the orbital, and takes on the values, l = 0, 1, 2, …, n – 1. We will learn what these shapes are in the next section. This means that an orbital with n = 1 can have only one value of l, l = 0, whereas n = 2 permits l = 0 and l = 1, and so on. The principal quantum number defines the general size and energy of the orbital. The l value specifies the shape of the orbital. Orbitals with the same value of l form a subshell.

Magnetic Quantum Number

Angular momentum is a vector.  Electrons with angular momentum can have this momentum oriented in different directions.  In quantum mechanics it is convenient to describe the z component of the angular momentum. The magnetic quantum number, called ml, specifies the z component of the angular momentum for a particular orbital. For example, if l = 0, then the only possible value of ml is zero. When l = 1, ml can be equal to –1, 0, or +1. Generally speaking, ml can be equal to the set of numbers [–l, –(l –1), …, –1, 0, +1, …, (l – 1), l]. The total number of possible orbitals with the same value of l (a subshell) is 2l + 1. Thus, there is one orbital with l = 0 (ml = 0 is the only orbital), there are three orbitals with l = 1 (ml = -1, ml = 0, ml = 1), five orbitals with l = 2 (ml = -2, ml = -1, ml = 0, ml = 1, ml = 2), and so on.

Rather than specifying all the values of n and l every time we refer to a subshell or an orbital, chemists use an abbreviated system with lowercase letters to denote the value of l for a particular subshell or orbital. Orbitals with l = 0 are called s orbitals (or the s subshell). The value l = 1 corresponds to the p orbitals. For a given n, p orbitals constitute a p subshell (e.g., 3p subshell if n = 3). The orbitals with l = 2 are called the d orbitals, followed by the f, g, and h orbitals for l = 3, 4, 5, and there are higher values we will not consider. When naming a subshell, it is common to write the principal quantum number (n) followed by the subshell letter (s, p, d, f, etc). For example, when referring to a subshell with n = 4 and l = 2, we would call this the 4d subshell. We can also say that there are five different 4d orbitals since there are five values for ml.

As a review, the principal quantum number defines the general value of the electronic energy, with lower values of n indicating lower (more negative) energies and electrons that are closer to the nucleus. The azimuthal quantum number determines the shape of the orbital and we can use s, p, d, f, etc. to designate which subshell the electron is in. And the magnetic quantum number specifies orientation of the orbital in space. Table 1 below provides the possible combinations of n, l, and ml for the first four shells. You’ll notice that every shell does not contain all shapes of orbitals because of the allowable values for the azimuthal quantum number (e.g., there is not a 1p orbital—only shells higher than n = 1 contain a p subshell).

Table 1. Summary of atomic orbitals and allowable quantum numbers.
n l Orbital notation ml Number of orbitals in a subshell Number of orbitals in a shell
1 0 1s 0 1 1
2 0 2s 0 1 4
1 2p -1, 0, +1 3
3 0 3s 0 1 9
1 3p -1, 0, +1 3
2 3d -2, -1, 0, +1, +2 5
4 0 4s 0 1 16
1 4p -1, 0, +1 3
2 4d -2, -1, 0, +1, +2 5
3 4f -3, -2, -1, 0, +1, +2, +3 7

Example 2

Working with Shells and Subshells
Indicate the number of subshells, the number of orbitals in each subshell, and the values of l and ml for the orbitals in the n = 4 shell of an atom.

Solution
For n = 4, l can have values of 0, 1, 2, and 3. Thus, four subshells are found in the n = 4 shell of an atom. For l = 0, ml can only be 0. Thus, there is only one orbital with n = 4 and l = 0. For l = 1, ml can have values of –1, 0, +1, so we find three orbitals. For l = 2, ml can have values of –2, –1, 0, +1, +2, so we have five orbitals. When l = 3, ml can have values of –3, –2, –1, 0, +1, +2, +3, and we can have seven orbitals. Thus, we find a total of 16 orbitals in the n = 4 shell of an atom.

Check Your Learning
How many orbitals are in the n = 5 shell?

Answer:

25 orbitals

Key Concepts and Summary

Macroscopic objects act as particles. Microscopic objects (such as electrons) have properties of both a particle and a wave. Their exact trajectories cannot be determined. The quantum mechanical model of atoms describes the three-dimensional position of the electron in a probabilistic manner according to a mathematical function called a wavefunction, often denoted as ψ. Atomic wavefunctions are also called orbitals and describe the areas in an atom where electrons are most likely to be found.

An atomic orbital is characterized by three quantum numbers. The principal quantum number, n, can be any positive integer. The relative energy of an orbital and the average distance of an electron from the nucleus are related to n. Orbitals having the same value of n are said to be in the same shell. The azimuthal quantum number, l, can have any integer value from 0 to n – 1. This quantum number describes the shape or type of the orbital. Orbitals with the same principal quantum number and the same l value belong to the same subshell. The magnetic quantum number, ml, with 2l + 1 values ranging from –l to +l, describes the orientation of the orbital in space.

Glossary

angular momentum quantum number (l)
quantum number distinguishing the different shapes of orbitals; it is also a measure of the orbital angular momentum
atomic orbital
mathematical function that describes the behavior of an electron in an atom (also called the wavefunction), it can be used to find the probability of locating an electron in a specific region around the nucleus, as well as other dynamical variables
magnetic quantum number (ml)
quantum number signifying the orientation of an atomic orbital around the nucleus; orbitals having different values of ml but the same subshell value of l have the same energy (are degenerate), but this degeneracy can be removed by application of an external magnetic field
principal quantum number (n)
quantum number specifying the shell an electron occupies in an atom
quantum mechanics
field of study that includes quantization of energy, wave-particle duality, and the Heisenberg uncertainty principle to describe matter
shell
set of orbitals with the same principal quantum number, n
subshell
set of orbitals in an atom with the same values of n and l
wavefunction (ψ)
mathematical description of an atomic orbital that describes the shape of the orbital; it can be used to calculate the probability of finding the electron at any given location in the orbital, as well as dynamical variables such as the energy and the angular momentum

Chemistry End of Section Exercises

  1. How are the Bohr model and the quantum mechanical model of the hydrogen atom similar? How are they different?
  2. Answer the following questions:
    1. Without using quantum numbers, describe the differences between the shells, subshells, and orbitals of an atom.
    2. How do the quantum numbers of the shells, subshells, and orbitals of an atom differ?
  3. Describe the wavefunction and in what ways Schrödinger built upon de Broglie’s previous work.
  4. Which of the following equations describe particle-like behavior? Which describe wavelike behavior? Do any involve both types of behavior? Describe the reasons for your choices.
    1. c = \lambda\nu
    2. E = h\nu
    3. \lambda = \frac{h}{m\nu}
  5. Three sets of quantum numbers are listed below (n, l, ml). Select the invalid set.
    1. (2, 0, 0)
    2. (3, 1, 3)
    3. (6, 5, –4)
  6. True or False: The larger the mass of a particle, the smaller its wavelength.

Answers to Chemistry End of Section Exercises

  1. Both models have a central positively charged nucleus with electrons moving about the nucleus in accordance with the Coulomb electrostatic potential. The Bohr model assumes that the electrons move in circular orbits that have quantized energies, angular momentum, and radii that are specified by a single quantum number, n = 1, 2, 3, …, but this quantization is an ad hoc assumption made by Bohr to incorporate quantization into an essentially classical mechanics description of the atom. Bohr also assumed that electrons orbiting the nucleus normally do not emit or absorb electromagnetic radiation, but do so when the electron switches to a different orbit. In the quantum mechanical model, the electrons do not move in precise orbits. There are inherent limitations in determining simultaneously both the position and energy of a quantum particle like an electron, an outcome of the Heisenberg uncertainty principle, so precise orbits are not possible. Instead, a probabilistic interpretation of the electron’s position at any given instant is used, with a mathematical function ψ called a wavefunction that can be used to determine the electron’s spatial probability distribution. These wavefunctions, or orbitals, are three-dimensional stationary waves that can be specified by three quantum numbers that arise naturally from their underlying mathematics (no ad hoc assumptions required): the principal quantum number, n (the same one used by Bohr), which specifies shells such that orbitals having the same n all have the same energy and approximately the same spatial extent; the angular momentum quantum number l, which is a measure of the orbital’s angular momentum and corresponds to the orbitals’ general shapes, as well as specifying subshells such that orbitals having the same l (and n) all have the same energy; and the orientation quantum number m, which is a measure of the z component of the angular momentum and corresponds to the orientations of the orbitals. The Bohr model gives the same expression for the energy as the quantum mechanical expression and, hence, both properly account for hydrogen’s discrete spectrum (an example of getting the right answers for the wrong reasons, something that many chemistry students can sympathize with), but gives the wrong expression for the angular momentum (Bohr orbits necessarily all have non-zero angular momentum, but some quantum orbitals [s orbitals] can have zero angular momentum).
  2. (a) Shells describe the general size of an orbital (or distance from the nucleus), subshells describe the shape of an orbital, and the actual orbitals include additional information about the orientation of the orbital.
    (b) the quantum numbers for shells are integers starting from n = 1, for subshells they are integers with values of 0 … (n – 1), for orbitals they are integers with values of –l … +l.
  3. Wavefunctions are mathematical functions describing energy and position of electrons in an atom. Building on deBroglie’s work, Schrodinger described the electrons as three-dimensional stationary waves. This was also further extended by Born to show that the square of wavefunction is the probability of finding a quantum particle (electron) in a certain location.
  4. (a) wavelike behavior because it is describing the relationship between wavelength and frequency of a wave.
    (b) particle-like behavior because it is describing the energy of a particle (photon) with frequency ν.
    (c) both because it is describing that a particle with mass m can have a wavelength λ.
  5. B
  6. True
Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 103/104 Resource Book Copyright © by Chem 103 Textbook Team and Chem 104 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.