M4Q6: Molarity, Solutions, and Dilutions

Introduction

The section explores solution concentrations, dilutions, and solution stoichiometry. This section includes worked examples, sample problems, and a glossary.

Learning Objectives for Solution Stoichiometry

| Key Concepts and Summary | Key Equations | Glossary | End of Section Exercises |

In preceding sections, we focused on the composition of substances: samples of matter that contain only one type of element or compound. However, mixtures—samples of matter containing two or more substances physically combined—are more commonly encountered in nature than are pure substances. Similar to a pure substance, the relative composition of a mixture plays an important role in determining its properties. The relative amount of oxygen in a planet’s atmosphere determines its ability to sustain aerobic life. The relative amounts of iron, carbon, nickel, and other elements in steel (a mixture known as an “alloy”) determine its physical strength and resistance to corrosion. The relative amount of the active ingredient in a medicine determines its effectiveness in achieving the desired pharmacological effect. The relative amount of sugar in a beverage determines its sweetness (Figure 1). In this section, we will describe one of the most common ways in which the relative compositions of mixtures may be quantified.

A picture is shown of sugar being poured from a spoon into a cup.
Figure 1. Sugar is one of many components in the complex mixture known as coffee. The amount of sugar in a given amount of coffee is an important determinant of the beverage’s sweetness. (credit: Jane Whitney)

Solutions & Molarity

We have previously defined solutions as homogeneous mixtures, meaning that the composition of the mixture (and therefore its properties) is uniform throughout its entire volume. Solutions occur frequently in nature and have also been implemented in many forms of manmade technology.

The relative amount of a given solution component is known as its concentration. Often, though not always, a solution contains one component with a concentration that is significantly greater than that of all other components. This component is called the solvent and may be viewed as the medium in which the other components are dispersed, or dissolved. Solutions in which water is the solvent are, of course, very common on our planet. A solution in which water is the solvent is called an aqueous solution (indicated by (aq) in a chemical reaction).

A solute is a component of a solution that is typically present at a much lower concentration than the solvent. Solute concentrations are often described with qualitative terms such as dilute (of relatively low concentration) and concentrated (of relatively high concentration).

Concentrations may be quantitatively assessed using a wide variety of measurement units, each convenient for particular applications. Molarity (M), or molar concentration, is a useful concentration unit for many applications in chemistry. Molarity is defined as the number of moles of solute in exactly 1 liter (1 L) of the solution:

M = \dfrac{\text{mol solute}}{\text{L solution}}

Students often get confused with the use of the terms molarity and molar. The terms molarity and molar are synonymous, but have different uses. For example, if you have a solution that is labeled “3.5 M”. We could say that the molarity (or molar concentration) of the solution is 3.5, or we could say that the solution is 3.5 molar. We would not typically read “3.5 M” as “3.5 molarity”.

Also notice that due to the definition of molarity, if you are provided with a molarity, you are inherently provided with a conversion factor between moles of solute and liters of solution (this is similar to how we can think about density as a conversion factor, or ratio, of mass to volume of a substance).

Example 1

Calculating Molar Concentrations
A 355 mL soft drink sample contains 0.133 mol of sucrose (table sugar). What is the molar concentration of sucrose in the beverage?

Solution
Since the moles of solute and the volume of solution are both given, the molarity can be calculated using the definition of molarity. Per this definition, the solution volume must be converted from mL to L:

M = \dfrac{\text{mol solute}}{\text{L solution}}  =  \dfrac{0.133 \;\text{mol}}{355 \;\text{mL} \times \frac{1 \;\text{L}}{1000 \;\text{mL}}} = 0.375 M

Check Your Learning
A teaspoon of table sugar contains about 0.01 mol sucrose. What is the molarity of sucrose if a teaspoon of sugar has been dissolved in a cup of tea with a volume of 200 mL?

Answer:

0.05 M

Example 2

Deriving Moles and Volumes from Molar Concentrations
How much sugar (mol) is contained in a modest sip (~10 mL) of the soft drink from Example 1?

Solution
In this case, we can rearrange the definition of molarity to isolate the quantity sought, moles of sugar. We then substitute the value for molarity that we derived in Example 1, 0.375 M:

M = \dfrac{\text{mol solute}}{\text{L solution}}

mol solute = M × L solution

mol solute = 0.375 \dfrac{\text{mol sugar}}{\text{L}} × (10 \;\text{mL} \times \dfrac{1\ \text{L}}{1000 \;\text{mL}}) = 0.004 mol sugar

Here we are using molarity as a conversion factor—since we know molarity and volume, we can find moles of substance.

Check Your Learning
What volume (mL) of the sweetened tea described in Example 1 contains the same amount of sugar (mol) as 10 mL of the soft drink in this example?

Answer:

80 mL

Example 3

Calculating Molar Concentrations from the Mass of Solute
Distilled white vinegar (Figure 2) is a solution of acetic acid, CH3CO2H, in water. A 0.500 L vinegar solution contains 25.2 g of acetic acid. What is the concentration of the acetic acid solution in units of molarity?

A label on a container is shown. The label has a picture of a salad with the words “Distilled White Vinegar,” and, “Reduced with water to 5% acidity,” written above it.
Figure 2. Distilled white vinegar is a solution of acetic acid in water.

Solution
As in the previous examples, the definition of molarity is the primary equation used to calculate the quantity sought. In this case, the mass of solute is provided instead of the amount of moles, so we must use the solute’s molar mass to obtain the amount of solute in moles:

M = \dfrac{\text{mol solute}}{\text{L solution}} = \dfrac{25.2 \;\text{g CH}_3\text{CO}_2\text{H}\times\frac{1 \;\text{mol CH}_2\text{CO}_2\text{H}}{60.052 \;\text{g CH}_2\text{CO}_2\text{H}}}{0.500 \;\text{L solution}}  =  0.839 \dfrac{\text{mol solute}}{\text{L solution}} = 0.839 M

Check Your Learning
Calculate the molarity of 6.52 g of CoCl2 (128.9 g/mol) dissolved in an aqueous solution with a total volume of 75.0 mL.

Answer:

0.674 M

Example 4

Determining the Mass of Solute in a Given Volume of Solution
How many grams of NaCl are contained in 0.250 L of a 5.30 M solution?

Solution
The volume and molarity of the solution are specified, so the amount (mol) of solute is easily computed as demonstrated in Example 2:

M = \dfrac{\text{mol solute}}{\text{L solution}}

mol solute = M × L solution

mol solute = 5.30 \dfrac{\text{mol NaCl}}{\text{L}} × 0.250 L = 1.325 mol NaCl

Finally, this molar amount is used to derive the mass of NaCl:

1.325 mol NaCl × \dfrac{58.44\;\text{g NaCl}}{\text{mol NaCl}} = 77.4 g NaCl

Another way of solving this problem, thinking of the concentration as a conversion factor between moles of solute and liters of solution is:

0.250 L solution × \dfrac{5.30\;\text{mol NaCl}}{1\;\text{L solution}} × \dfrac{58.44\;\text{g NaCl}}{1\;\text{mol NaCl}} = 77.4 g NaCl

Check Your Learning
How many grams of CaCl2 (110.98 g/mol) are contained in 250.0 mL of a 0.200 M solution of calcium chloride?

Answer:

5.55 g CaCl2

When performing calculations stepwise, as in Example 4, it is important to refrain from rounding any intermediate calculation results, which can lead to rounding errors in the final result. In Example 4, the molar amount of NaCl computed in the first step, 1.325 mol, would be properly rounded to 1.32 mol if it were to be reported; however, although the last digit (5) is not significant, it must be retained as a guard digit in the intermediate calculation. If we had not retained this guard digit, the final calculation for the mass of NaCl would have been 77.1 g, a difference of 0.3 g.

In addition to retaining a guard digit for intermediate calculations, we can also avoid rounding errors by performing computations in a single step (see Example 5). This eliminates intermediate steps so that only the final result is rounded.

Example 5

Determining the Volume of Solution Containing a Given Mass of Solute
In Example 3, we found the typical concentration of vinegar to be 0.839 M. What volume of vinegar contains 75.6 g of acetic acid?

Solution
First, use the molar mass to calculate moles of acetic acid from the given mass:

g solute × \dfrac{\text{mol solute}}{\text{g solute}} = mol solute

Then, use the molarity of the solution to calculate the volume of solution containing this molar amount of solute:

mol solute × \dfrac{\text{L solution}}{\text{mol solute}} = L solution

Combining these two steps into one yields:

g solute × \dfrac{\text{mol solute}}{\text{g solute}} × \dfrac{\text{L solution}}{\text{mol solute}} = L solution

75.6 g CH3CO2H × \dfrac{1\;\text{mol}\;\text{CH}_{3}\text{CO}_{2}\text{H}}{60.05\;\text{g}\;\text{CH}_{3}\text{CO}_{2}\text{H}} × \dfrac{\text{L solution}}{0.839\;\text{mol}\;\text{CH}_{3}\text{CO}_{2}\text{H}} = 1.50 L solution

Check Your Learning
What volume of a 1.50 M KBr solution contains 66.0 g KBr?

Answer:

0.370 L

Dilution of Solutions

Dilution is the process whereby the concentration of a solution is lessened by the addition of solvent. For example, we might say that a glass of iced tea becomes diluted as the ice melts. The water from the melting ice increases the volume of the solvent (water) and the overall volume of the solution (iced tea), thereby reducing the relative concentrations of the solutes that give the beverage its taste (Figure 3).

This figure shows two graduated cylinders side-by-side. The first has about half as much blue liquid as the second. The blue liquid is darker in the first cylinder than in the second.
Figure 3. Both solutions contain the same mass of copper nitrate. The solution on the right is more dilute because the copper nitrate is dissolved in more solvent. (credit: Mark Ott)

Dilution is also a common means of preparing solutions of a desired concentration. By adding solvent to a measured portion of a more concentrated stock solution, we can achieve a particular concentration. For example, commercial pesticides are typically sold as solutions in which the active ingredients are far more concentrated than is appropriate for their application. Before they can be used on crops, the pesticides must be diluted. This is also a very common practice for the preparation of a number of common laboratory reagents (Figure 4).

This figure shows two photos. In the first, there is an empty glass container, 4.75 g of K M n O subscript 4 powder on a white circle, and a bottle of distilled water. In the second photo the powder and about half the water have been added to the glass container. The liquid in the glass container is almost black in color.
Figure 4. A solution of KMnO4 is prepared by mixing water with 4.74 g of KMnO4 in a flask. (credit: modification of work by Mark Ott)

A simple mathematical relationship can be used to relate the volumes and concentrations of a solution before and after the dilution process. According to the definition of molarity, the amount of moles of solute (n) in a solution is equal to the product of the solution’s molarity (M) and its volume in liters (L):

n = M × L

Expressions like these may be written for a solution before and after it is diluted:

n1 = M1 × L1
n2 = M2 × L2

where the subscripts “1” and “2” refer to the solution before and after the dilution, respectively. Since the dilution process does not change the amount of solute in the solution, n1 = n2. Thus, these two equations may be set equal to one another:

M1 × L1 = M2 × L2

This relation is commonly referred to as the dilution equation. Although we derived this equation using molarity as the unit of concentration and liters as the unit of volume, other units of concentration and volume may be used, so long as the units properly cancel per dimensional analysis. Reflecting this versatility, the dilution equation is often written in the more general form:

C1 × V1 = C2 × V2

where C and V are concentration and volume, respectively.

 

Use the simulation to explore the relationship between solute amount, solution volume, and concentration and to confirm the dilution equation.

Example 6

Determining the Concentration of a Diluted Solution
If 0.850 L of a 5.00 M solution of copper nitrate, Cu(NO3)2, is diluted to a volume of 1.80 L by the addition of water, what is the molarity of the diluted solution?

Solution
We are given the volume and concentration of a stock solution, V1 and C1, and the volume of the resultant diluted solution, V2. We need to find the concentration of the diluted solution, C2. We thus rearrange the dilution equation in order to isolate C2:

C1 × V1 = C2 × V2

C2 = \dfrac{\text{C}_{1}\text{V}_{1}}{\text{V}_{2}}

Since the stock solution is being diluted by more than two-fold (volume is increased from 0.85 L to 1.80 L), we would expect the diluted solution’s concentration to be less than one-half 5 M. We will compare this ballpark estimate to the calculated result to check for any gross errors in computation (for example, such as an improper substitution of the given quantities). Substituting the given values for the terms on the right side of this equation yields:

C2 = \dfrac{0.850\;\text{L}\;\times\; 5.00\;\frac{\text{mol}}{\text{L}}}{1.80\;\text{L}} = 2.36 M

This result compares well to our ballpark estimate (it’s a bit less than one-half the stock concentration, 5 M).

Check Your Learning
What is the concentration of the solution that results from diluting 25.0 mL of a 2.04 M solution of CH3OH to 500.0 mL?

Answer:

0.102 M CH3OH

Example 7

Volume of a Diluted Solution
What volume of 0.12 M HBr can be prepared from 11 mL (0.011 L) of 0.45 M HBr?

Solution
We are given the volume and concentration of a stock solution, V1 and C1, and the concentration of the resultant diluted solution, C2. We need to find the volume of the diluted solution, V2. We thus rearrange the dilution equation in order to isolate V2:

C1 × V1 = C2 × V2

V2 = \dfrac{\text{C}_{1}\text{V}_{1}}{\text{C}_{2}}

Since the diluted concentration (0.12 M) is slightly more than one-fourth the original concentration (0.45 M), we would expect the volume of the diluted solution to be roughly four times the original volume, or around 44 mL. Substituting the given values and solving for the unknown volume yields:

V2 = \dfrac{(0.45\;\text{M})(0.011\;\text{L})}{0.12\;\text{M}} = 0.041 L

The volume of the 0.12 M solution is 0.041 L (41 mL). The result is reasonable and compares well with our rough estimate.

Check Your Learning
A laboratory experiment calls for 0.125 M HNO3. What volume of 0.125 M HNO3 can be prepared from 0.250 L of 1.88 M HNO3?

Answer:

3.76 L

Example 8

Volume of a Concentrated Solution Needed for Dilution
What volume of 1.59 M KOH is required to prepare 5.00 L of 0.100 M KOH?

Solution
We are given the concentration of a stock solution, C1, and the volume and concentration of the resultant diluted solution, V2 and C2. We need to find the volume of the stock solution, V1. We thus rearrange the dilution equation in order to isolate V1:

C1 × V1 = C2 × V2

V1 = \dfrac{\text{C}_{2}\text{V}_{2}}{\text{C}_{1}}

Since the concentration of the diluted solution 0.100 M is roughly one-sixteenth that of the stock solution (1.59 M), we would expect the volume of the stock solution to be about one-sixteenth that of the diluted solution, or around 0.3 liters. Substituting the given values and solving for the unknown volume yields:

V1 = \dfrac{(0.100\;\text{M})(5.00\;\text{L})}{1.59\;\text{M}} = 0.314 L

Thus, we would need 0.314 L of the 1.59 M solution to prepare the desired solution. This result is consistent with our rough estimate.

Check Your Learning
What volume of a 0.575 M solution of glucose, C6H12O6, can be prepared from 50.00 mL of a 3.00 M glucose solution?

Answer:

0.261 L

Solution Stoichiometry

In an earlier section, we learned that the coefficients of a balanced chemical equation provide the relative numbers of the chemical species, allowing a quantitative assessment of the relationships between the amounts of substances consumed and produced by the reaction. The process of using the coefficients in a balanced chemical equation to relate the amount of reactants and products can be summarized as in Figure 5.

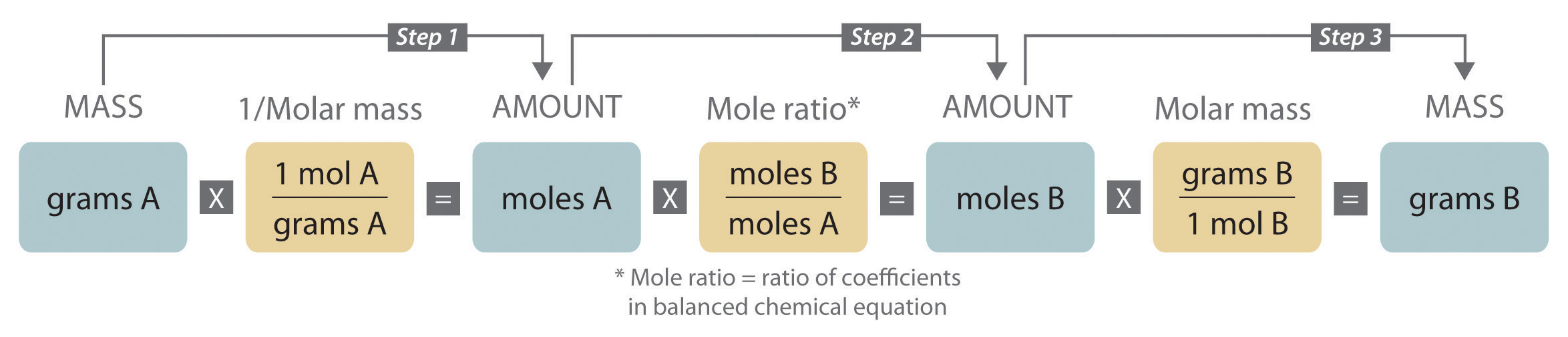
A flow chart for stoichiometric calculations is shown. There are 7 boxes arranged horizontally. The first is shaded blue and labeled, “grams A”. A multiplication sign is between the first and second box. The second box is shaded yellow and labeled “1 mol A divided by grams A”. The second box is followed by an equal sign. The third box is shaded blue and labeled “moles A”. The third box is followed by a multiplication sign. The fourth box is shaded yellow and labeled “moles B divided by moles A”. The fourth box is followed by an equal sign. The fifth box is shaded blue and labeled “moles B”. The fifth box is followed by a multiplication sign. The sixth box is shaded yellow and labeled “grams B divided by 1 mol B”. The sixth box is followed by an equal sign. The seventh and final box is shaded blue and labeled “grams B”. Above the first box, there is a label that says “Mass”. Above the second box a label say “1 divided by molar mass”. Above the third box a label says “amount”. An arrow points from the first box to the third box and says “step 1”. Above the fourth box a label says “mole ratio”, which is defined as the ratio of coefficients in balanced chemical equation. Above the fifth box a label says “amount”. An arrow points from the third box to the fifth box and says “step 2”. A label above the sixth box says “molar mass”. A label above the seventh box says “mass”. An arrow points from the fifth box to the seventh box and says “Step 3”.
Figure 5. A flowchart for stoichiometric calculations involving pure substances. The molar masses of the reactants and the products are used as conversion factors so that you can calculate the mass of product from the mass of reactant and vice versa.

Since solutions offer a convenient medium for carrying out chemical reactions, it is often necessary to know how much of one solution will react with a given quantity of another. We can perform calculations similar to those outlined in Figure 5 by first using the volume of the solution and the concentration of the solution to determine how many moles of solute are present. This process is outlined in Figure 6.

A flow chart for stoichiometric calculations is shown. There are 7 boxes arranged horizontally. The first is shaded blue and labeled, “liters solution”. A multiplication sign is between the first and second box. The second box is shaded yellow and labeled “moles A divided by 1 liter”. The second box is followed by an equal sign. The third box is shaded blue and labeled “moles A”. The third box is followed by a multiplication sign. The fourth box is shaded yellow and labeled “moles B divided by moles A”. The fourth box is followed by an equal sign. The fifth box is shaded blue and labeled “moles B”. The fifth box is followed by a multiplication sign. The sixth box is shaded yellow and labeled “grams B divided by 1 mol B”. The sixth box is followed by an equal sign. The seventh and final box is shaded blue and labeled “grams B”. Above the first box, there is a label that says “Volume”. Above the second box a label say “Molarity”. Above the third box a label says “Moles”. Above the fourth box a label says “mole ratio”, which is defined as the ratio of coefficients in balanced chemical equation. Above the fifth box a label says “Moles”. A label above the sixth box says “molar mass”. A label above the seventh box says “mass”.
Figure 6. Flowchart for stoichiometric calculations of reactions in solution. The volume and concentration of a solution can be used to determine the moles of a substance, which can then be used to calculate the amount of another substance required or produced in the reaction.

The initial goal is the same for both procedures—convert to moles. You can accomplish this by either using mass and molar mass of a substance or by using volume and concentration of a solution. Once you have determined how many moles of a reactant or product are present, you can use the stoichiometric mole ratio to determine the quantity of the other reactants or products in the reaction.

Example 9

Solution Stoichiometry

Gold is extracted from its ores by treatment with an aqueous cyanide solution, which causes a reaction that forms the soluble [Au(CN)2]− ion. Gold is then recovered by reduction with metallic zinc according to the following equation:

Zn(s) + 2 [Au(CN)2]–(aq)  →  [Zn(CN)4]2-(aq) + 2 Au(s)

What mass of gold would you expect to recover from 400.0 L of a 3.30 × 10−4 M solution of [Au(CN)2]−?

Solution

First, we check the chemical equation to make sure it is balanced as written. Then we calculate the number of moles of [Au(CN)2]− present by multiplying the volume of the solution by its concentration. From the balanced chemical equation, we then use a mole ratio to calculate the number of moles of gold that can be obtained from the reaction. To calculate the mass of gold recovered, we multiply the number of moles of gold by its molar mass.

We can adapt Figure 6 to show this process as follows:

A flow chart for stoichiometric calculations is shown. There are 7 boxes arranged horizontally. The first is shaded blue and labeled, “400.0 liters”. A multiplication sign is between the first and second box. The second box is shaded yellow and labeled “3.30e-4 moles [Au(CN) subscript 2]- divided by 1 liter”. The second box is followed by an equal sign. The third box is shaded blue and labeled “0.132 mol [Au(CN) subscript 2]-”. The third box is followed by a multiplication sign. The fourth box is shaded yellow and labeled “2 moles Au divided by 2 moles [Au(CN) subscript 2]-“. The fourth box is followed by an equal sign. The fifth box is shaded blue and labeled “0.132 mole Au”. The fifth box is followed by a multiplication sign. The sixth box is shaded yellow and labeled “196.67 g Au divided by 1 mol Au”. The sixth box is followed by an equal sign. The seventh and final box is shaded blue and labeled “26.0 g Au”.

Check Your Learning

What mass of solid lanthanum(III) oxalate nonahydrate [La2(C2O4)3·9H2O] (molar mass = 703.87 g/mol) can be obtained from 650 mL of a 0.0170 M aqueous solution of LaCl3 by adding a stoichiometric amount of sodium oxalate (Na2C2O4)? The unbalanced reaction is as follows:

LaCl3(aq) + Na2C2O4(s) + H2O(ℓ)  →  La2(C2O4)3·9H2O(s) + NaCl(aq)

Answer:

3.89 g

Example 10

Limiting Reactants in Solution

When aqueous solutions of silver nitrate and potassium dichromate are mixed, an exchange reaction occurs, and silver dichromate is obtained as a red solid. The overall chemical equation for the reaction is as follows:

2 AgNO3(aq) + K2Cr2O7(aq)  →  Ag2Cr2O7(s) + 2 KNO3(aq)

What mass of Ag2Cr2O7 is formed when 500 mL of 0.17 M K2Cr2O7 are mixed with 250 mL of 0.57 M AgNO3?

Solution

First, calculate the number of moles of each reactant by multiplying the volume of each solution by its molarity.

mol K2Cr2O7 = 500 mL × \dfrac{1\;\text{L}}{1000\;\text{mL}} × \dfrac{0.17\;\text{mol}\;\text{K}_{2}\text{Cr}_{2}\text{O}_{7}}{1\;\text{L}} = 0.085 mol K2Cr2O7

mol AgNO3 = 250 mL × \dfrac{1\;\text{L}}{1000\;\text{mL}} × \dfrac{0.57\;\text{mol}\;\text{AgNO}_{3}}{1\;\text{L}} = 0.14 mol AgNO3

Then, determine the limiting reactant by calculating the moles of Ag2Cr2O7 produced if each reactant were completely reacted.

0.085 mol K2Cr2O7 × \dfrac{1\;\text{mol}\;\text{Ag}_{2}\text{Cr}_{2}\text{O}_{7}}{1\;\text{mol}\;\text{K}_{2}\text{Cr}_{2}\text{O}_{7}} = 0.085 mol Ag2Cr2O7

0.14 mol AgNO3   \dfrac{1\;\text{mol}\;\text{Ag}_{2}\text{Cr}_{2}\text{O}_{7}}{2\;\text{mol}\;\text{AgNO}_{3}} = 0.071 mol Ag2Cr2O7

Since complete reaction of AgNO3 produces less product (Ag2Cr2O7), AgNO3 is the limiting reactant and K2Cr2O7 is the excess reactant.

To find what mass of Ag2Cr2O7 is formed, we use the molar mass (431.72 g/mol):

0.071 mol Ag2Cr2O7 × \dfrac{431.72\;\text{g}\;\text{Ag}_{2}\text{Cr}_{2}\text{O}_{7}}{1\;\text{mol}\;\text{Ag}_{2}\text{Cr}_{2}\text{O}_{7}} = 30.8 g Ag2Cr2O7

Check Your Learning

Aqueous solutions of sodium bicarbonate and sulfuric acid react to produce carbon dioxide according to the following equation:

2 NaHCO3(aq) + H2SO4(aq)  →  2 CO2(g) + Na2SO4(aq) + 2 H2O(ℓ)

If 13.0 mL of 3.0 M H2SO4 are added to 732 mL of 0.112 M NaHCO3, what mass of CO2 is produced?

Answer:

3.4 g

Key Concepts and Summary

Solutions are homogeneous mixtures. Many solutions contain one component, called the solvent, in which other components, called solutes, are dissolved. An aqueous solution is one for which the solvent is water. The concentration of a solution is a measure of the relative amount of solute in a given amount of solution. Concentrations may be measured using various units, with one very useful unit being molarity, defined as the number of moles of solute per liter of solution. The solute concentration of a solution may be decreased by adding solvent, a process referred to as dilution. The dilution equation is a simple relation between concentrations and volumes of a solution before and after dilution.

We can perform stoichiometric calculations for reactions that occur in solution by using the volume and concentration of the solution to determine the moles of substance present. Stoichiometric factors then work the same as before to convert between moles of reactants and products.

Key Equations

  • M = \dfrac{\text{mol solute}}{\text{L solution}}
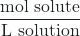
  • C1 × V1 = C2 × V2
  • Percent by mass = 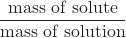\dfrac{\text{mass of solute}}{\text{mass of solution}} × 100

Glossary

aqueous solution
solution for which water is the solvent
concentrated
qualitative term for a solution containing solute at a relatively high concentration
concentration
quantitative measure of the relative amounts of solute and solvent present in a solution
dilute
qualitative term for a solution containing solute at a relatively low concentration
dilution
process of adding solvent to a solution in order to lower the concentration of solutes
dissolved
describes the process by which solute components are dispersed in a solvent
mass percentage
ratio of solute-to-solution mass expressed as a percentage
mass-volume percent
ratio of solute mass to solution volume, expressed as a percentage
molarity (M)
unit of concentration, defined as the number of moles of solute dissolved in 1 liter of solution
parts per billion (ppb)
ratio of solute-to-solution mass multiplied by 109
parts per million (ppm)
ratio of solute-to-solution mass multiplied by 106
solute
solution component present in a concentration less than that of the solvent
solvent
solution component present in a concentration that is higher relative to other components
volume percentage
ratio of solute-to-solution volume expressed as a percentage

Chemistry End of Chapter Exercises

Molarity
  1. Explain what changes and what stays the same when 1.00 L of a solution of NaCl is diluted to 1.80 L.
  2. What does it mean when we say that a 200-mL sample and a 400-mL sample of a solution of salt have the same molarity? In what ways are the two samples identical? In what ways are these two samples different?
  3. Determine the molarity for each of the following solutions:
    1. 0.444 mol of CoCl2 in 0.654 L of solution
    2. 98.0 g of phosphoric acid, H3PO4, in 1.00 L of solution
    3. 0.2074 g of calcium hydroxide, Ca(OH)2, in 40.00 mL of solution
    4. 10.5 kg of Na2SO4·10H2O in 18.60 L of solution
    5. 7.0 × 10−3 mol of I2 in 100.0 mL of solution
    6. 1.8 × 104 mg of HCl in 0.075 L of solution
  4. Consider this question: What is the mass of the solute in 0.500 L of 0.30 M glucose, C6H12O6, used for intravenous injection?
    1. Outline the steps necessary to answer the question.
    2. Answer the question.
  5. Calculate the number of moles and the mass of the solute in each of the following solutions:
    1. 2.00 L of 18.5 M H2SO4, concentrated sulfuric acid
    2. 100.0 mL of 3.8 × 10−5M NaCN, the minimum lethal concentration of sodium cyanide in blood serum
    3. 5.50 L of 13.3 M H2CO, the formaldehyde used to “fix” tissue samples
    4. 325 mL of 1.8 × 10−6M FeSO4, the minimum concentration of iron sulfate detectable by taste in drinking water
  6. Consider this question: What is the molarity of KMnO4 in a solution of 0.0908 g of KMnO4 in 0.500 L of solution?
    1. Outline the steps necessary to answer the question.
    2. Answer the question.
  7. Calculate the molarity of each of the following solutions:
    1. 0.195 g of cholesterol, C27H46O, in 0.100 L of serum, the average concentration of cholesterol in human serum
    2. 4.25 g of NH3 in 0.500 L of solution, the concentration of NH3 in household ammonia
    3. 1.49 kg of isopropyl alcohol, C3H7OH, in 2.50 L of solution, the concentration of isopropyl alcohol in rubbing alcohol
    4. 0.029 g of I2 in 0.100 L of solution, the solubility of I2 in water at 20 °C
  8. There is about 1.0 g of calcium, as Ca2+, in 1.0 L of milk. What is the molarity of Ca2+ in milk?
  9. If 0.1718 L of a 0.3556-M C3H7OH solution is diluted to a concentration of 0.1222 M, what is the volume of the resulting solution?
  10. What volume of a 0.33-M C12H22O11 solution can be diluted to prepare 25 mL of a solution with a concentration of 0.025 M?
  11. What is the molarity of the diluted solution when each of the following solutions is diluted to the given final volume?
    1. 1.00 L of a 0.250-M solution of Fe(NO3)3 is diluted to a final volume of 2.00 L
    2. 0.5000 L of a 0.1222-M solution of C3H7OH is diluted to a final volume of 1.250 L
    3. 2.35 L of a 0.350-M solution of H3PO4 is diluted to a final volume of 4.00 L
    4. 22.50 mL of a 0.025-M solution of C12H22O11 is diluted to 100.0 mL
  12. What is the final concentration of the solution produced when 225.5 mL of a 0.09988-M solution of Na2CO3 is allowed to evaporate until the solution volume is reduced to 45.00 mL?
  13. A 2.00-L bottle of a solution of concentrated HCl was purchased for the general chemistry laboratory. The solution contained 868.8 g of HCl. What is the molarity of the solution?
  14. An experiment in a general chemistry laboratory calls for a 2.00-M solution of HCl. How many mL of 11.9 M HCl would be required to make 250 mL of 2.00 M HCl?
  15. The US Environmental Protection Agency (EPA) places limits on the quantities of toxic substances that may be discharged into the sewer system. Limits have been established for a variety of substances, including hexavalent chromium, which is limited to 0.50 mg/L. If an industry is discharging hexavalent chromium as potassium dichromate (K2Cr2O7), what is the maximum permissible molarity of that substance?
  16. 375.0 mL of a 0.473 M solution of magnesium hydroxide is diluted to a total volume of 675.0 mL.
    1. What is the formula of magnesium hydroxide?
    2. What is the hydroxide ion concentration in the resulting solution?
  17. You have a solution of aluminum chloride.
    1. Write the formula of aluminum chloride.
    2. Determine the concentration of chloride ions in a 0.250 M solution of aluminum chloride.
  18. Determine the total number of ions, in moles, present in 100.0 mL of a 0.500 M solution of sodium phosphate.
  19. Write the formula for lead(II) nitrate, and determine the total number of moles of ions present in 150. mL of 0.500 M lead(II) nitrate.
Solution Stoichiometry
  1. In a beaker, 150. mL of a 0.500 M silver(I) nitrate solution is mixed with 250. mL of a 0.250 M potassium chromate solution and a solid is collected.
    1. Write the complete balanced equation for this reaction.
    2. What is the name and formula for the solid collected?
    3. How much solid is collected (in grams)?
  2. How much 0.496 M sodium hydroxide is required to completely neutralize 20.0 mL of 0.809 M hydrochloric acid?
  3. How many grams of lead(II) iodide (molar mass  =  461.00 g/mol) is collected if 60.0 mL of 0.300 M potassium iodide is mixed with 25.0 mL of 0.540 M lead(II) nitrate? Assume 100% yield for this reaction.
  4. Mixing solutions of KBr and Pb(ClO4)2 causes a precipitation.
    1. Write the balanced chemical equation for this reaction.
    2. Determine the volume (in mL) of a 0.855 M Pb(ClO4)2 solution that would be required to completely react with 450.0 mL of a 0.545 M solution of KBr.
  5. 0.703 g of an unknown acid, H2A, is dissolved in water. It takes 54.8 mL of 0.273 M KOH to completely react with the acid using the following reaction:
    H2A(aq) + 2 KOH(aq)  →  K2A(aq) + 2 H2O(ℓ)

    Determine the molar mass of the unknown acid.

  6. A mass of 0.4113 g of an unknown acid, HA, reacts completely with 28.10 mL of 0.1055 M NaOH. What is the molar mass of the acid?
    HA(aq) + NaOH(aq)  →  NaA(aq) + H2O(ℓ)

Answers to Chemistry End of Chapter Exercises

  1. Molarity of NaCl changes; Moles of NaCl remains the same
  2. These two samples have the same mole:volume ratio; These two samples have different total volume and different individual amount of moles per volume
  3. (a) 0.679 M; (b) 1.00 M; (c) 0.06998 M; (d) 1.75 M; (e) 0.070 M; (f) 6.6 M
  4. (a) determine the number of moles of glucose in 0.500 L of solution; determine the molar mass of glucose; determine the mass of glucose from the number of moles and its molar mass
    (b) 27 g
  5. (a) 37.0 mol H2SO4; 3.63 × 103 g H2SO4
    (b) 3.8 × 10−6 mol NaCN; 1.9 × 10−4 g NaCN
    (c) 73.2 mol H2CO; 2.20 kg H2CO
    (d) 5.9 × 10−7 mol FeSO4; 8.9 × 10−5 g FeSO4
  6. (a) Determine the molar mass of KMnO4; determine the number of moles of KMnO4 in the solution; from the number of moles and the volume of solution, determine the molarity
    (b) 1.15 × 10−3M
  7. (a) 5.04 × 10−3M; (b) 0.499 M; (c) 9.92 M; (d) 1.1 × 10−3M
  8. 0.025 M
  9. 0.4999 L
  10. 1.9 mL
  11. (a) 0.125 M; (b) 0.04888 M; (c) 0.206 M; (d) 0.0056 M
  12. 0.501 M
  13. 11.9 M
  14. 42.0 mL
  15. Maximum permissible molarity: 4.81×10-6 M
  16. (a) Mg(OH)2; (b) 0.526 M
  17. (a) AlCl3; (b) 0.750 M
  18. 0.200 moles
  19. Pb(NO3)2; 0.225 moles of ions
  20. (a) 2 AgNO3(aq) + K2CrO4(aq) → Ag2CrO4(s) + 2 KNO3(aq)
    (b) silver(I) chromate, Ag2CrO4
    (c) 12.4 g Ag2CrO4 (AgNO3 is the limiting reactant)
  21. 32.6 mL
  22. 4.15 g
  23. (a) Pb(ClO4)2(aq) + 2 KBr(aq)  →  PbBr2(s) + 2 KClO4(aq)
    (b) 143 mL

    Left-click here to watch Exercise 23 problem solving video.

  24. 94.0 g/mol
  25. 138.7 g/mol
Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 103/104 Resource Book Copyright © by Chem 103 Textbook Team and Chem 104 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.