M13Q6: Integrated Rate Laws and the Method of Half-Lives

Learning Objectives
  • Know the meaning of half-life, t½, and use t½ in calculations.
  • Given the initial concentration of a reactant, use the integrated rate law to determine the concentration of reactant after a given time has passed or how long it will take for the reactant to reach a given concentration.
    | First Order | Second Order | Zero Order |
  • Evaluate experimental data using the half-lives method to determine whether a reaction is first order.

| Key Concepts and Summary | Key Equations | Glossary | End of Section Exercises |

The Half-Life of a Reaction

The half-life of a reaction (t½) is the time required for one-half of a given amount of reactant to be consumed. In each succeeding half-life, half of the remaining concentration of the reactant is consumed.

Determining the Half-Life for First-Order Reactions

We can rearrange the first-order integrated rate law equation:

ln[A]t  =  –kt  +  ln[A]0

to solve for time:

t = \left(\dfrac{1}{k}\right)\left(\ln\left(\dfrac{[\text{A}]_{0}}{[\text{A}]_{t}}\right)\right)

If we set the time, t, equal to the half-life, t½, and the corresponding concentration of A at this time is equal to one-half of its initial concentration, or ½[A]0 = [A]t. Therefore:

t½ = \left(\dfrac{1}{k}\right)\left(\ln\left(\dfrac{[\text{A}]_{0}}{\frac{1}{2}[\text{A}]_{0}}\right)\right) = \left(\dfrac{1}{k}\right)\left(\ln\dfrac{1}{\frac{1}{2}}\right) = \left(\dfrac{1}{k}\right)(ln 2) = \dfrac{\ln 2}{k}

You will sometimes see this equation simplified to:

t½ = \dfrac{0.693}{k}

The half-life of a first-order reaction is inversely proportional to the rate constant, k. A fast reaction (shorter half-life) will have a larger k; a slow reaction (longer half-life) will have a smaller k.

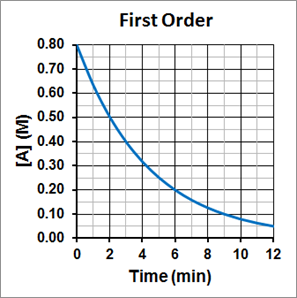
It is also important to notice that the half-life for a first-order reaction is independent of the concentration of the reactant. The half-life remains constant regardless of how much reactant was there in the beginning of the reaction and how much of the reactant remains. This can be seen in Figure 1, where the initial concentration of A is 0.80 M, and it take 3 minutes to reach half its initial concentration, or 0.4 M. For the concentration to again decrease by half,  to 0.20 M, it again takes 3 minutes. For the concentration to again decrease by half, to 0.10 M, it again takes 3 minutes. The half-life is consistently 3.0 minutes.

Figure 1. A first-order graph of [A] (M) vs time (min).

Example 1

Calculation of a First-order Rate Constant using Half-Life
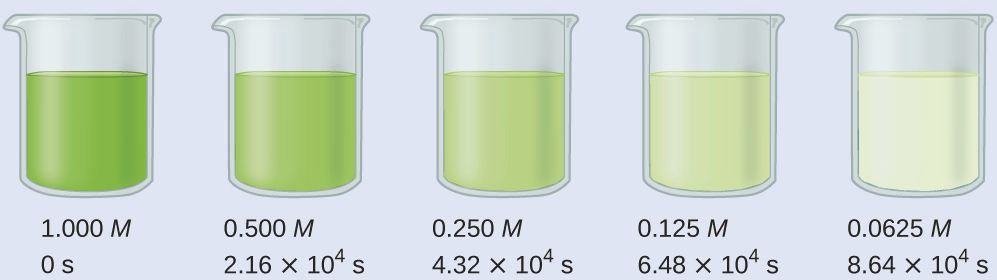
Calculate the rate constant for the decomposition of hydrogen peroxide in water at 40 °C, using the data given in Figure 2.

A diagram of 5 beakers is shown, each approximately half-filled with colored substances. Beneath each beaker are three rows of text. The first beaker contains a bright green substance and is labeled below as, “1.000 M, 0 s.” The second beaker contains a slightly lighter green substance and is labeled below as, “0.500 M, 2.16 times 10 superscript 4 s.” The third beaker contains an even lighter green substance and is labeled below as, “0.250 M, 4.32 times 10 superscript 4 s.” The fourth beaker contains a green tinted substance and is labeled below as, “0.125 M, 6.48 times 10 superscript 4 s.” The fifth beaker contains a colorless substance and is labeled below as, “0.0625 M, 8.64 times 10 superscript 4 s.”
Figure 2. The decomposition of H2O2 (2 H2O2  ⟶  2 H2O + O2) at 40 °C is illustrated. The intensity of the color symbolizes the concentration of H2O2 at the indicated times; however, H2O2 is actually colorless.

Solution:

Examining the data given reveals that the time for the concentration to decrease by half is 2.16 × 104 seconds, regardless of how much H2O2 remains. From this, we can deduce that it is a first-order reaction and that t½  =  2.16 × 104 s.

After determining the half-life, it can be used to find k:

k  = \dfrac{\ln 2}{t_{1/2}} = \dfrac{\ln 2}{ 2.16 \times 10^{4}\;\text{s}}  =  3.21 x 10-5 s-1

Check Your Learning
The first-order radioactive decay of iodine-131 exhibits a rate constant of 0.138 days−1. What is the half-life for this decay?

Answer:

5.02 days.

Determining the Half-Life for Second-Order Reactions

We can apply the same strategy we used to find the half-life equation for a first-order reaction to a second-order reaction. First rearrange the second-order rate law to solve for t:

\dfrac{1}{[\text{A}]_{t}} = kt + \dfrac{1}{[\text{A}]_{0}}

t = \left(\dfrac{1}{k}\right)\left(\dfrac{1}{[\text{A}]_{t}} - \dfrac{1}{[\text{A}]_{0}}\right)

Set the time, t, equal to the half-life, t½, and the corresponding concentration of A at this time is equal to one-half of its initial concentration, or ½[A]0 = [A]t. Substituting these into the previous equation results in the second-order half-life equation:

t½ = \left(\dfrac{1}{k}\right)\left(\dfrac{1}{\frac{1}{2}[\text{A}]_{0}} - \dfrac{1}{[\text{A}]_{0}} \right) = \left(\dfrac{1}{k}\right) \left(\dfrac{1}{[\text{A}]_{0}} \right) = \dfrac{1}{k[\text{A}]_0}

Unlike with first-order reactions, the rate constant of a second-order reaction cannot be calculated directly from the half-life unless the initial concentration is known.

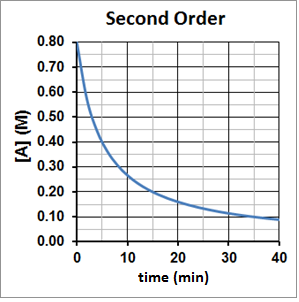
For a second-order reaction, t½ is inversely proportional to the concentration of the reactant, and the half-life increases as the reaction proceeds because the concentration of reactant decreases. This can be seen graphically in Figure 3. It takes five minutes for A to decompose from 0.80 M to 0.40 M, ten minutes for A to decompose from 0.40 M to 0.20 M and twenty minutes for A to then decompose from 0.20 M to 0.10 M.

Figure 3. Plot of a second-order reaction with [A] (M) vs time (min).

Determining the Half-Life for Zero-Order Reactions

We can repeat the same strategy again with a zero-order reaction. Solving the original integrated rate law for time and substituting in time, t, equal to the half-life, t½, and the corresponding concentration of A at this time is equal to one-half of its initial concentration, or ½[A]0 = [A]t, will result in the zero-order half-life equation:

[A]t = –kt + [A]0

t = \left(\dfrac{1}{k}\right)([A]t – [A]0)

t½ = \left(\dfrac{1}{k}\right)(½[A]0 – [A]0) = \dfrac{[\text{A}]_{0}}{2k}

As with second-order reactions, the rate constant of a zero-order reaction cannot be calculated directly from the half-life unless the initial concentration is known.

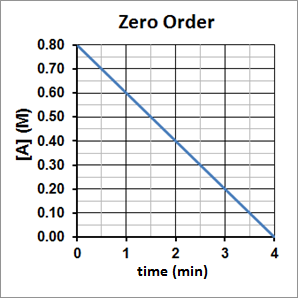
The half-life of a zero-order reaction is directly proportional to the initial concentration of the reactant and so the half-life will decrease as the reaction concentration decreases. This can be seen experimentally in Figure 4. It takes two minutes for A to decompose from 0.80 M to 0.40 M and then one minute for A to decompose from 0.40 M to 0.20 M and 30 seconds for A to then decompose from 0.20 M to 0.10 M.

Figure 4. A plot of a zero-order reaction with [A] (M) vs time (min)

Key Concepts and Summary

The half-life of a reaction, the time it takes for one-half of a reactant to be consumed, is useful in the sense that it is a common percentage of decay in order to compare various reactions, like radioactivity. It also helps us know whether a reaction is first, second, or zero order, since the time it takes for 100% of a reactant to decay to 50% and the time from 50% to 25% are not the same. In a first order reaction, the half-life is always constant throughout a reaction. For a second-order reaction, the half-life doubles as the concentration halves. And for a zero-order reaction, the half-life halves as the concentration halves.

Key Equations

  • First order: t½ = \dfrac{\ln 2}{k}
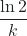
  • Second order: t½ = \dfrac{1}{k[\text{A}]_0}
  • Zero order: t½ =  \dfrac{[\text{A}]_{0}}{2k}

Glossary

half-life (t½)
the time required for one-half of a given amount of reactant to be consumed. In each succeeding half-life, half of the remaining concentration of the reactant is consumed.

Chemistry End of Section Exercises

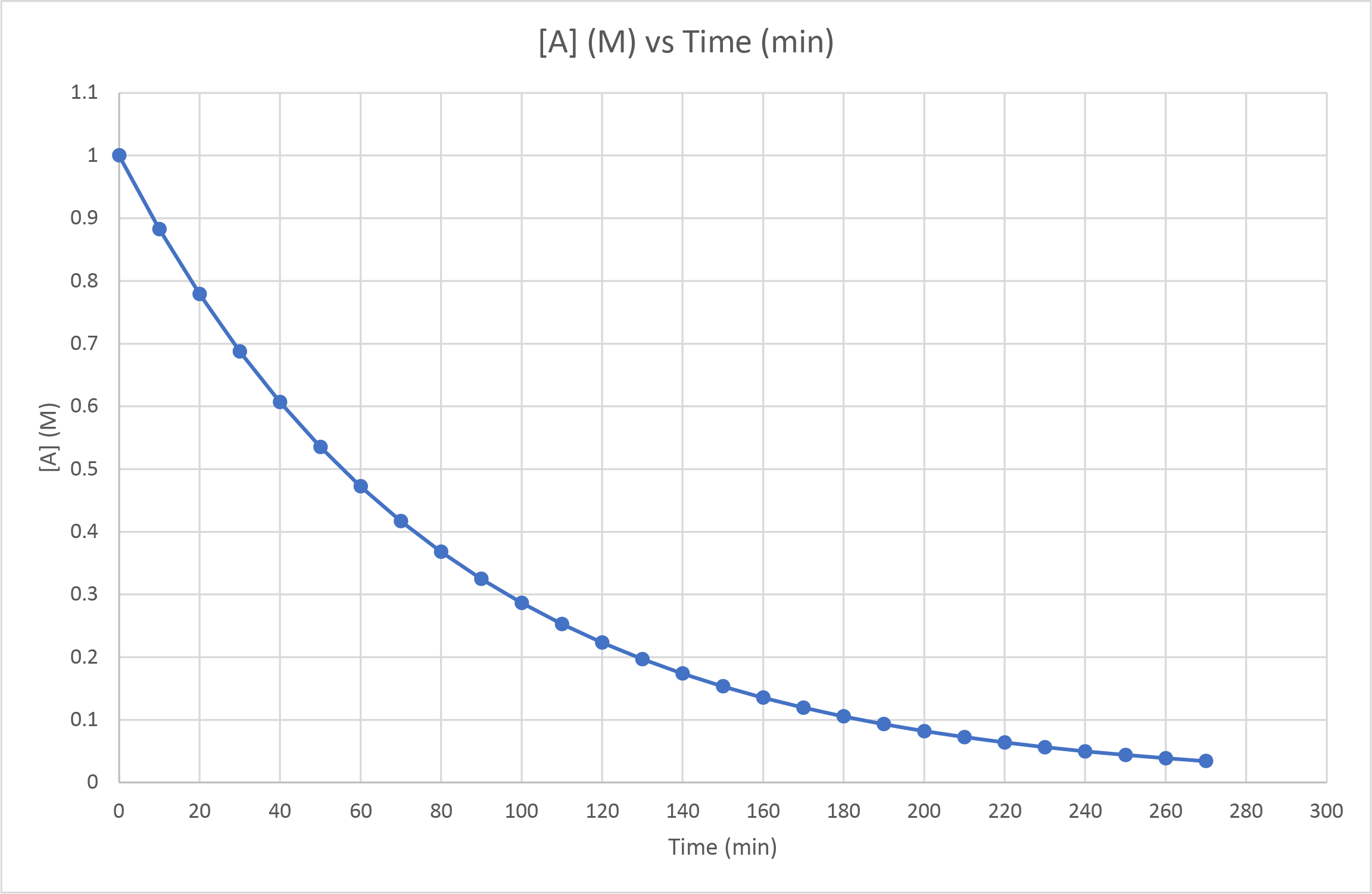
  1. The concentration of A was observed as it decomposed to form B. The following graph was produced. Is this a zero-, first- or second-order reaction? How can you tell? What would you observe if it had been a different order reaction?
  2. For which order reaction does the half-life get longer as the initial concentration increases?
    1. Zero-order
    2. First-order
    3. Second-order
    4. None of them. Half-life is always independent of the initial concentration.
  3. A very odd meteor was formed of equal amounts rubidium-87 (t½ = 48.8 billion years), beryllium-10 (t½ = 1.6 × 106 years), aluminum-26 (t½ = 730,000 years), and krypton-81 (t½ = 2.1 × 105 years). After traveling across the universe, which of these isotopes will remain in the greatest quantity? Assume all isotopes will undergo first-order radioactive decay.
  4. What is the half-life for the first-order decay of phosphorus-32? The rate constant for the decay is 4.85 × 10−2 day−1.

    _{15}^{32}\text{P}   →  _{16}^{32}\text{S} + _{-1}^{0}\beta

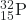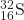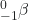
  5. What is the half-life for the first-order decay of carbon-14? The rate constant for the decay is 1.21 × 10−4 year−1.

    _{12}^{6}\text{C}   →  _{12}^{7}\text{N} + _{-1}^{0}\beta

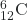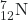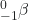
  6. What is the half-life for the decomposition of NOCl when the concentration of NOCl is 0.15 M? The rate constant for this second-order reaction is 8.0 × 10−8 M-1s-1.
  7. Fluorine-18 is a radioactive isotope that decays by positron emission to form oxygen-18 with a half-life of 109.7 min (a positron is a particle with the mass of an electron and a single unit of positive charge). Physicians use flourine-18 to study the brain by injecting a quantity of fluoro-substituted glucose into the blood of a patient. The glucose accumulates in the regions where the brain is active and needs nourishment.
    1. What is the rate constant for the decomposition of fluorine-18?
    2. If a sample of glucose containing radioactive fluorine-18 is injected into the blood, what percent of the radioactivity will remain after 5.49 hr?
  8. Both technetium-99 and thallium-201 are used to image heart muscle in patients with suspected heart problems. The half-lives are 6 h and 73 h, respectively. What percent of the radioactivity would remain for each of the isotopes after 2 days (48 h)?
  9. The reaction of compound A to give compounds C and D was found to be second-order in A. The rate constant for the reaction was determined to be 2.42 M-1s-1. If the initial concentration of A is 0.500 M, what is the value of t½?
  10. The half-life of a reaction of compound A to give compounds D and E is 8.50 min when the initial concentration of A is 0.150 M.
    1. How long will it take for the concentration to drop to 0.0500 M if the reaction is (a) first order with respect to A or (b) second order with respect to A or (c) zero order with respect to A?
    2. How long will it take for the concentration to drop from 0.0500 M to 0.0250 M if the reaction is (a) first order with respect to A or (b) second order with respect to A or (c) zero order with respect to A?
  11. There are two molecules with the formula C3H6: Propene, CH3CH=CH2, a reactant used to form the polymer polypropylene (used for indoor-outdoor carpets), and cyclopropane, used as an anesthetic. When heated to 499 °C, cyclopropane rearranges (isomerizes) and forms propene with a rate constant of 5.95 × 10-4 s-1. What is the half-life of this reaction (in hr)? What fraction of the cyclopropane remains after 0.75 hr at 499 °C?
  12. Sildenafil is a drug that is removed from the body in a process that follows first order kinetics with k = 0.20 hr-1. How long does it take for the level of Sildenafil in the blood to fall to 10% of the original concentration?
  13. If it takes 3.4 years for a radioactive isotope to decay to 1/16 of its initial value, what is the value of k for the isotope?

Answers to Chemistry End of Section Exercises

  1. First-order. Measuring the half-life at various points across the span of the reaction gives a consistent value of approximately 55 seconds (ie from 1.0 M to 0.50 M, from 0.50 M to 0.25 M, from 0.60 M to 0.30 M). First-order reaction half-lives are unaffected by the reactant concentration. If it had been a second-order reaction, the half-live would increase as the reactant concentration decreases. Second-order reaction half-lives would decrease with decreased reactant concentration.
  2. A
  3. Rubidium-87. The largest half-life would correspond to the smallest k and the slowest decay reaction.
  4. 14.3 days
  5. 5730 years
  6. 8.3 × 107 s
  7. (a) k = 6.319  × 10-3 min-1; (b) 12.5%
  8. 0.391%; 63.4%
  9. 0.826 s
  10. (a) First-order: k = 0.0815 min-1, t = 13.5 min; Second-order: k = 0.784 M-1 min-1, t = 17.0 min; Zero-order: k = 0.00882 M min-1, t = 11.3 min
    (b) First-order: k = 0.0815 min-1, t = 8.50 min; Second-order: k = 0.784 M-1 min-1, t = 25.5 min; Zero-order: k = 0.00882 M min-1, t = 2.83 min

    Left-click here to watch Exercise 10 problem solving video.

  11. 0.324 hr; 20% remains
  12. 12 hours
  13. 0.82 years-1
Comments
Please use this form to report any inconsistencies, errors, or other things you would like to change about this page. We appreciate your comments. 🙂

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chem 103/104 Resource Book Copyright © by Chem 103 Textbook Team and Chem 104 Textbook Team is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.